Негосударственное общеобразовательное учреждение Средняя общеобразовательная школа

Какой порядок действий в математике: Порядок действий в примерах по математике

alexxlab

Порядок действий в примерах по математике

Опубликовано от Admin — Оставить комментарий

В статье рассмотрим порядок действий в примерах по математике, которые содержат скобки, умножение, деление, сложение и вычитание. В статье также приведены примеры, начиная от простых и заканчивая сложными.

Правила выполнения действий для решения примеров:
  1. Сначала вычислить то, что находится в скобках. Если скобок нет, то переходим к следующему пункту.
  2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию. Если нет умножения или деления, то переходим к следующему пункту.
  3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию.

 

Пример 1.    12 –  3 + 2 + 5  

Читаем его слева направо:
1) 12 — 3 = 9. Запишем число 9 в главном выражении ➜  9+2+5

2) 9 + 2 = 11. Запишем число 11 в главном выражении ➜  11+5
3) 11 + 5 = 16.
Ответ: 12 — 3 + 2 + 5 = 16

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

          1          2           3     
12  – 3  +  2  +  5  =  16

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

          1          2           3     
12  – 3  +  2  +  5  =  9 + 2 + 5 = 11 + 5 = 16

 

Пример 2.    12 – (7 + 2) + 5 × 3  

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
1) сначала вычислить то, что находится в скобках: 7+2=9. Запишем полученное число 9 в главном выражении вместо выражения в скобках ➜  12-9+5×3

2) вычислить умножение и деление: 5×3=15. Запишем полученное число 15 в главном выражении ➜  12-9+15
3) вычислить сложение и вычитание: 12-9+15.

         3         1          4       2
12 – (7 + 2) + 5 × 3  =   12 – 9 + 5 × 3 = 12 – 9 + 15 = 3 + 15 = 18
 
Пример 3.   20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)  

Расставим порядок действий.

         6       3         7          4        1          5        8             2
20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

1) Действие в скобках будет первым. Так как в примере скобки встречаются два раза, то выполняем действия в скобках по порядку 7-3=4 и 12-7=5
2) далее выполняется умножение и деление в порядке следования
3) и последним выполняется умножение и деление в порядке следования

                 6        3        7         4         1          5       8             2
1) 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7) = 20 – 5 × 3 + 24 : 4 × 2 + 5 =
2) 20 – 5 × 3 + 24 : 4 × 2 + 5 = 20 – 15 + 6 × 2 + 5 = 20 – 15 + 12 + 5 =
3) 20 – 15 + 12 + 5 = 5 + 12 + 5 = 17 + 5 = 22

Таким образом, для правильного решения примеров по математике необходимо правильно определить порядок действий в примерах.

Для тренировки решения примеров по математике на порядок действий можно скачать программы:

  • Порядок действий в пределах 20 (сложение и вычитание)
  • Порядок действий в пределах 100 (все действия)
  • Порядок действий в пределах 1000 (все действия)
  • Сложные примеры на порядок действий

Для освоения темы вам также могут понадобится темы: раскрытие скобок и законы математики.

Рубрика: Для школьников

Метка Математика

Порядок действий в математике

Метки
Головоломки Досуг Задачи Логика Математика Смекалка

Порядок выполнения действий в математике нередко становится настоящим камнем преткновения. Мы изучали его в начальных классах школы и, по идее, должны помнить всю жизнь. Но теория, как говорил Мефистофель, суха. Да и кому, по правде говоря, интересны примеры, где порядок действий расписан заранее?

© Depositphotos

Другое дело — задания из нашей подборки. В них тебе дается лишь набор цифр и число, которое нужно получить. А какие действия и в каком порядке выполнять, решать только тебе. И тут уж ответ не вычислишь, а тем более не угадаешь. Ведь для решения необходимо мыслить и творчески, и аналитически. А это помогает нам успешно находить выход из самых сложных жизненных ситуаций.

Порядок действий в математике

  1. Начнем с примеров попроще. Поставь в записи 1 * 3 * 2 * 1 * 2 = 10 вместо звездочек знаки арифметических действий, чтобы получилось верное равенство. Попробуй найти как можно больше вариантов решения со скобками и без.
  2. У тебя есть четыре цифры: 5, 5, 5 и 1. С помощью сложения, вычитания, умножения, деления и скобок получи из них число 24, используя каждую из этих цифр только 1 раз.
  3. Используя цифры (1, 3, 4, 6), скобки и арифметические операции (сложение, вычитание, умножение, деление), получи число 24. Разрешается использовать только эти цифры и только эти операции. Каждую цифру можно использовать только один раз. Операции и скобки можно использовать любое число раз.© Depositphotos

Ответы

  1. Как я уже говорил, тут открывается широкий простор для творчества. Мне сходу удалось найти только одно решение без скобок: 1 + 3 х 2 + 1 + 2 = 10. И одно со скобками: 1 х (3 + 2) х 1 х 2 = 10. Но решений, скорее всего, намного больше. Попробуй найти недостающие!
  2. Я предложил эту задачку своим друзьям. И перед тем как назвать верный ответ, расскажу вам об ошибочных, а также весьма остроумных вариантах решения. Самый распространенный ответ:
    5 х 5 – 1 = 24    . Был еще такой вариант: 5 + 5 + 5 + 5 + 5 – 1 = 24. Да, ответ в обоих случаях, конечно, 24. Но как быть с условием? В нём четко сказано, что нужно использовать каждую из цифр и только 1 раз!

    © Depositphotos

    Интересное решение за пределами математики предложила девушка бариста. По ее словам, достаточно выпить 5 чашек кофе, затем еще 5 чашек и еще 5 чашек за один день, чтобы получить 24 часа бодрствования. Мы не советуем даже пробовать это повторить. Ведь больше 300 миллилитров бодрящего напитка в день способны навредить твоему здоровью. Но попытка свести воедино математику, кулинарию и физиологию заслуживает всяческого уважения.

    © Pexels

    Возвращаясь к математике, признаюсь, что найти решение для этого примера было очень непросто. У меня оно получилось таким: (5 — (1 : 5)) х 5= 24.

    Но, может, кто-нибудь из наших читателей найдет еще один вариант?

  3. Мы уже решили два примера. Поэтому с последним проблем быть не должно. И опять нас выручает деление на дробь:
    6 / ( 1 — ( 3 / 4 ) ) = 24.
    © Pexels

Как видишь, наши забавные задачки помогают провести время с пользой. Ведь сообразительность помогает искать необычные, интересные и простые пути решения, достигая результата не только в игре, но и в реальной жизни кратчайшим путем.

Поделиться

Порядок операций | Brilliant Math & Science Wiki

Бывший блестящий член, Матин Насери, Сатвик Голечха, а также

способствовал

Содержимое
  • Общие мнемоники для порядка операций
  • Сложение и умножение
  • Экспоненты
  • Скобки
  • Смотрите также

Есть два распространенных мнемонических приема для запоминания правильного порядка операций.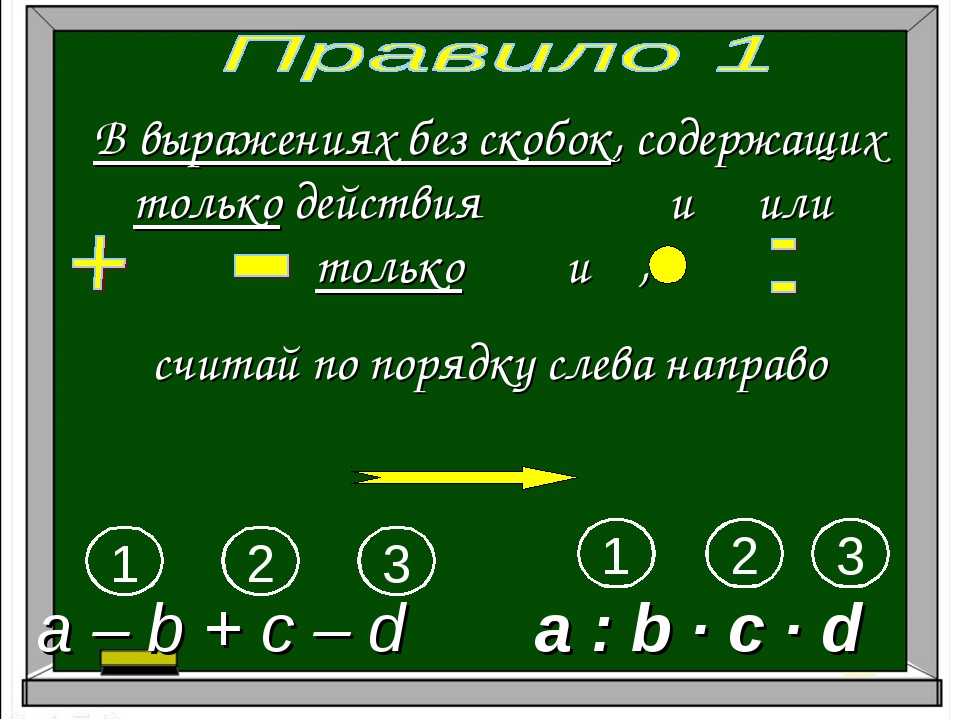 Однако при их использовании важно помнить, что истинный порядок операций определен выше, и, в частности, этот порядок операций не делает различий между умножением и делением (или сложением и вычитанием) при упорядочивании.

PEMDAS или «Пожалуйста, извините, моя дорогая тетя Салли»:

  • P арентесы
  • E     компоненты
  • М умножение
  • D ivision
  • A дополнение
  • S вычитание

БОДМАС:

  • B ракетки
  • O ряды (показатели и радикалы)
  • D ivision
  • M умножение
  • A дополнение
  • S вычитание

Обратите внимание, что наивное обращение с любым из них может привести к ошибкам, поскольку и сложение/вычитание, и умножение/деление должны группироваться и оцениваться слева направо. Более точной мнемоникой может быть PE(MD)(AS) и BO(DM)(AS).

Одним из требований является выполнение умножения перед сложением. Например, в выражении 2+3×4 2 + 3 х 4 2+3 х 4 мы получим ответ 5 х 4 = 20 5 х 4 = 20 5 х 4 = 20, если мы начнем с добавления 2 и 3, но мы получим 2 + 12 = 14 2 + 12 = 14 2 + 12 = 14, если сначала умножим. Поскольку важно, чтобы все интерпретировали выражение 2+3×4 2 + 3 \times 4 2+3×4 одинаково, мы просто

определите правильный порядок, в котором умножение выполняется первым. Таким образом, 2+3×4=2+(3×4)=2+12=14 2 + 3 х 4 = 2 + ( 3 х 4 ) = 2 + 12 = 14 2+3 х 4=2+ (3×4)=2+12=14.

Сколько будет 2×4+3×5 2×4+3×5 2×4+3×5?

Следуя правильному порядку операций, мы видим, что мы должны вычислить 2×4 2 \times 4 2×4 и 3×5 3 \times 5 3×5, прежде чем делать какое-либо сложение.

Таким образом, правильный ответ: 2×4+3×5=8+15=23 2 х 4 + 3 х 5 = 8 + 15 = 23 2 х 4 + 3 х 5 = 8 + 15 = 23. □_\квадрат□​

Что такое 48÷2×12? 48 \дел 2 \умножить на 12 ? 48÷2×12?

Если бы мы небрежно следили за PEMDAS, ответом было бы сначала выполнить умножение, что дало бы нам 48÷24=2 48 \div 24 = 2 48÷24=2.

Однако это неверно.

Мы не делаем различий между умножением и делением, а выполняем их слева направо. Это дает

48÷2×12=24×12=288. □ 48 \дел 2 \умножить на 12 = 24 \умножить на 12 = 288. \ _\квадрат48÷2×12=24×12=288. □​ 92 = 361. \_\квадрат(3+42)2=(3+16)2=192=361. □​

  • Упрощение выражений
  • Рациональные показатели

Цитировать как: Порядок операций. Brilliant.org . Извлекаются из https://brilliant.org/wiki/order-of-operations/

1.3: Порядок операций

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    41986
    • Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Лин Чжоу Технологический колледж Нью-Йорка Сити CUNY
    • NY via технологий в CUNY Academic Works

    Что означает выражение «3 умножить на 4 плюс 5». Кто-то ответит 17, а кто-то 27. Почему? Чтобы устранить двусмысленность, мы можем написать

    \[(3 х 4)+5=17 \нечисло\]

    и

    \[3 \cdot(4+5)=27, \номер\]

    , где мы должны сначала оценить количество в скобках. Поскольку писать много круглых скобок может быть несколько громоздко, существует важное соглашение или соглашение, согласно которому, если мы просто пишем \(3 \times 4+5\), мы имеем в виду \((3 \times 4)+5 .\) То есть при отсутствии скобок мы должны умножить, прежде чем складывать. Это часть так называемого Порядка Операций. Это нужно помнить.

    Определение: 1.24: Порядок действий

    При вычислении выражения, включающего сложение, вычитание, умножение и деление, которое не имеет круглых скобок или показателей степени, мы сначала выполняем слева направо все операции умножения и деления. Затем слева направо сложение и вычитание. Если есть части выражения, заключенные в круглые скобки, сначала нужно оценить то, что находится внутри круглых скобок.

    Примечание 1.25

    Вычитание можно превратить в сложение, а затем сложение можно выполнять в любом порядке, не обязательно слева направо. Это объясняет, почему сложение и вычитание идут вместе в порядке операций. Будет аналогичное утверждение для умножения и деления, но оно будет отложено до обсуждения дробей.

    ‘PE(MD)(AS)’ — это простой способ запомнить порядок операций. Это означает, что порядок следующий: Скобки, Экспоненты (это будет включено позже), Умножение и Деление (взятые вместе слева направо) и, наконец, Сложение и Вычитание (взятые вместе слева направо).

    Давайте попробуем решить несколько задач.

    Пример 1.26

    1. \(3+2(3+5)=3+2(8)=3+16=19\)
    2. \(3-2(-4+7)=3-2(3)=3-6=-3\)
    3. \(-3-4-2(-2 \cdot 6-5)=-3-4-2(-12-5)=-3-4-2(-17)=-3-4-(- 34)=-3-4+34=27\)
    4. \(-(3-(-6))-(1-4 \cdot(-5)+4)=-(3+6)-(1-(-20)+4)=-9-(1 +20+4)=-9-25=-9+(-25)=-34\)
    5. \(-2(-14 \дел 7+7)=-2(-2+7)=-2(5)=-10\)
    6. \(-3(-2 \cdot 7-(-5)(4) \div 2)=-3(-14-(-20) \div 2)=-3(-14-(-10)) =-3(-4)=12\)
    7. \(6 \div 2 \times 3=3 \times 3=9\) Примечание: \(6 \div 2 \times 36=6 \div 6=1\)
    8. \(-2(3-1) 2-(8-22) \дел 4=-2(2) 2-(8-4) \дел 4=-2(4)-4 \дел 4=-8 -1=-9\)

    Выход Проблема

    Вычислить: \(\влево(3^{3}+5\вправо) \div 4-4(7-2)\)

    Эта страница под названием 1.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *