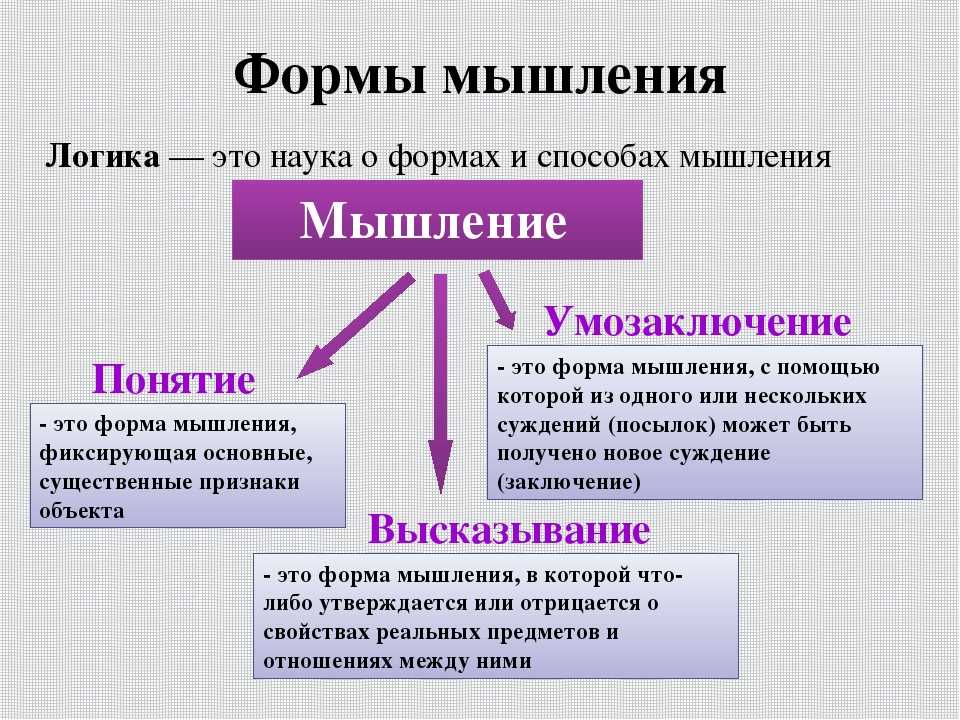
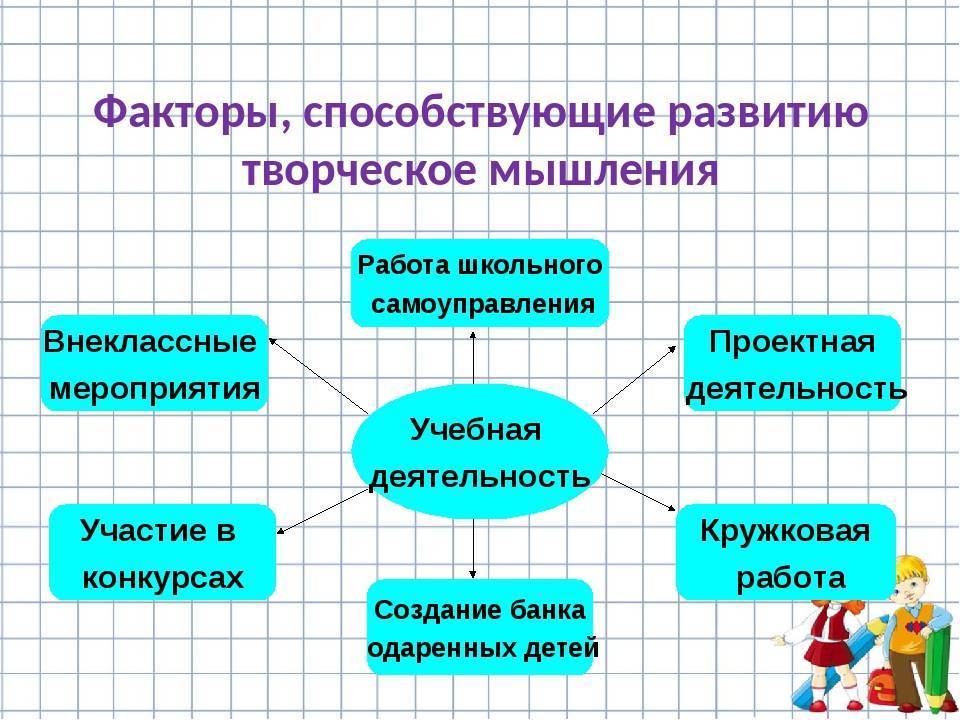
Качественное и количественное мышление . Интеллектуальная авантюра I [Истоки бытия]
Преимущества количественного мышления очевидны, на нем выстроена вся цивилизация. Люди легко обучаются ему, оно легко иллюстрируется, обеспечено огромным математическим аппаратом. Для кого-то в жизни достаточно таблицы умножения и правил сложения-вычитания-деления, а для других необходимы уже логарифмы, интегралы, функции. А для некоторых – нечеткие множества. Возможность упрощать и усложнять системы, просчитывать их – это безусловные преимущества. Безусловный минус: невозможно работать – ни мыслить, ни действовать – с целым. А значит, человек не может эффективно думать о себе, видеть себя, познать себя и изменять себя при желании и необходимости.
Наук о человеке (а мы помним, что человек – живой организм, а всякий живой организм – целое) огромное количество, но все это науки о частях, которые вне целого, как известно, тем же самым не являются, это уже другое. Печень отдельно от организма – это одна печень, даже если мы ее не жарим, а просто думаем о ней. А печень как часть
Печень отдельно от организма – это одна печень, даже если мы ее не жарим, а просто думаем о ней. А печень как часть
У нас даже нет инструмента, чтобы снять какие-нибудь показания не с отдельных органов, а с тела как целого. Единственный целостный показатель, который пришел нам от древних, – это так называемая аура. Сегодня есть прибор, установка, которая в режиме онлайн на мониторе показывает ауру – некое свечение, возникающее в сверхвысоких частотах вокруг человеческого организма. Дешифровать показания абсолютно достоверно пока не удается. И мы начинаем сочинять, интерпретировать… Так, благодаря тому, что некоторые из древних развили в себе способность видеть ауру мозгом, без приборов, они обнаружили все приборы, которые потом были сделаны, в самом человеке.
Мы не просто мало знаем о человеке, мы почти ничего не знаем о человеке, мы много знаем о его частях. Если мы корректные исследователи, мы понимаем, что исследуем не человека, а изъятые из него мысленно или немысленно части, которые теряют свою качественную определенность, будучи изъяты из целого.
Теперь посмотрим на другую сторону – качественное мышление.
Минус – огромная сложность передачи информации от одного сознания к другому. Огромная сложность создания адекватного языка описания и языка оперирования. Полное отсутствие математических инструментов, а значит, бесконечное подозрение в субъективности понимаемой как недостоверность. Еще один минус – непривычность. Поскольку весь опыт человечества в этой области мифологизирован, мистифицирован и зашифрован.
Именно поэтому, когда мы читаем эзотерические тексты, мы читаем что-то другое, чем то, о чем авторы писали. Каждый симультанный образ – это символ какого-то конкретного целого в его качественной определенности. Но поскольку нам неизвестен реальный контекст, что же они обозначали этими обозначающими, то мы сочиняем свою интерпретацию их описания. Так постепенно мы многое насочиняли…
Плюсы качественного мышления: возможность оперировать целыми объектами – и в сознании, в пространстве сознания, и в пространстве реальности. В перспективе получить ответ на самый главный вопрос: что же такое человек как целое? Сейчас ученые, занимающиеся электричеством, постепенно приходят к мнению, что единственный человек в истории науки и техники, который знал, что такое электричество, – это Никола Тесла. Но он не мог этого рассказать, даже если бы захотел. Он мог какой-нибудь симультанный образ выдать, но кому это помогает? Создал свою мифологическую систему симультанных образов, а техническую документацию всю уничтожил, понимая, какое это оружие. Он в дневнике написал: «Я мог бы расколоть земной шар пополам, но никогда не сделаю этого».
В перспективе получить ответ на самый главный вопрос: что же такое человек как целое? Сейчас ученые, занимающиеся электричеством, постепенно приходят к мнению, что единственный человек в истории науки и техники, который знал, что такое электричество, – это Никола Тесла. Но он не мог этого рассказать, даже если бы захотел. Он мог какой-нибудь симультанный образ выдать, но кому это помогает? Создал свою мифологическую систему симультанных образов, а техническую документацию всю уничтожил, понимая, какое это оружие. Он в дневнике написал: «Я мог бы расколоть земной шар пополам, но никогда не сделаю этого».
Качественная сторона сознания дает возможность распоряжаться гораздо большим энергетическим ресурсом реальности, чем количественная сторона. Самое большое преимущество качественной стороны сознания, оперирования качественного – это возможность создать мечту всех кибернетиков – металогику. Логику логик.
Кто будет знать хотя бы три слова из металогики – будет владеть миром.
| Comments: | ||||||||||||||||||||||||||||||||||||||||||||||||
И что, неужели кто-то умудряется отвечать неправильно?
«Кто-то из читателей этого ЖЖ» отличается от просто «кого-то» больше, чем средний ответивший на вопрос от не ответившего. 🙂 (без темы) — (Анонимно) Развернуть
Я совсем идиот в математике, но получилось.
+1 Редко когда в блоге Аввы удается почувствовать себя дееспособным.
Интересно, каков должен быть образ мышления, чтобы дать неправильный ответ?
Например: (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть
долго искал подвох: почему простое «арифметическое» решение может оказаться неправильным. В итоге они оказались правильными в обоих случаях.
Подсказка же есть в виде количества ответивших. Если бы был подвох, то было бы гораздо меньше.
даже среди образованных людей не считается позорным совсем плохо знать математику, даже плохо на уровне ребёнка, всё что выше таблицы умножения уже не является обязательным знанием. при этом типа очень стыдно делать какие-то ошибки в грамматике или орфографии, даже когда эти ошибки не влияют на точность передаваемой идеи. но то, что у большинства людей сложности с такими тривиальными вопросами это позорище в первую очередь для образовательной системы.
Позор — он, конечно, позор. Но боюсь, что результаты завышены по обеим выборкам. (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть
По ходу городок-то пенсионерский
Ага, в нем живет 400 дедок и 600 бабок. И половина из них поёт в хоре. Потому что больше на пенсии заняться нечем. (Удалённый комментарий)
В оригинале: What is the probability that a randomly drawn man is a member of the choir? Действительно, можно найти двусмысленность при желании. Но это задача не для тех, кто знает теорему Байеса. И она без подвоха.
Задачи, вообщем-то, довольно сложные и предполагают некоторое понимание вероятности. Я удивлен, что 10-15% отвечают на обе них правильно.
а третья там про грибы вообще гроб (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть
Правильный ответ на первый вопрос: неизвестно, случайно можно выбрать очень по-разному.
Ещё неизвестно, не записался ли кто-нибудь в хор, пока случайного мужчину выбирали
1. И тут про вакцинацию!! 2. Не хватает в условии: Предполагается ли, что нужно решать в уме. 3. Мой любимый вопрос про проценты: Что больше: «13% от 17» или «17% от 13».
а что больше после первого года: вклад €13 под 17% или вклад €17 под 13% годовых? А после ста лет? (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть (без темы) — (Анонимно) Развернуть
70 бросков — это тоже спойлер.
Да, конечно, лучше бы было 42. (Удалённый комментарий)
Угадал, хотя ждал подвоха. Странный город-гадюшник, в котором женщин в 1.5 раза больше, чем мужчин. На войну что-ли ушли?
На заработки уехали. Пением в хоре много не заработаешь.
Я решил, но пришлось рисовать на бумажке схемы и круги, ждал какого-то подвоха.
Для людей, которые удивляются почему не все отвечают правильно. Вы видели топ-20 постов в ФБ? В частности, есть пост, где предлагают объяснить как сложить 28 и 47, и порядка 4 миллионов комментариев к нему. Edited at 2021-09-22 18:41 (UTC)
Там честно пишут, что эти 20 топ-постов суммарно составляют менее 1% просмотренного контента. Просто кликбейты. (без темы) — (Анонимно) Развернуть
2. | ||||||||||||||||||||||||||||||||||||||||||||||||
Количественные навыки, мышление и рассуждение
Различные ресурсы, использующие количественное мышление в классе, доступны на веб-сайтах SERC. Ресурсы включают в себя обширные коллекции страниц проектов с учебными пособиями и примерами, а также обучающими мероприятиями на различных образовательных уровнях, некоторые из которых содержат визуализации, которые могут быть полезны для лекций или лабораторных работ.
Нажмите на изображение выше, чтобы просмотреть учебные задания, связанные с количественными навыками, мышлением и рассуждениями. Коллекции предоставляются преподавателями и могут включать работу с реальными данными, моделями и т. д.
Развитие количественного мышления: в этом модуле описывается, как инструктор может намеренно включать цели и задачи количественного мышления в свои занятия.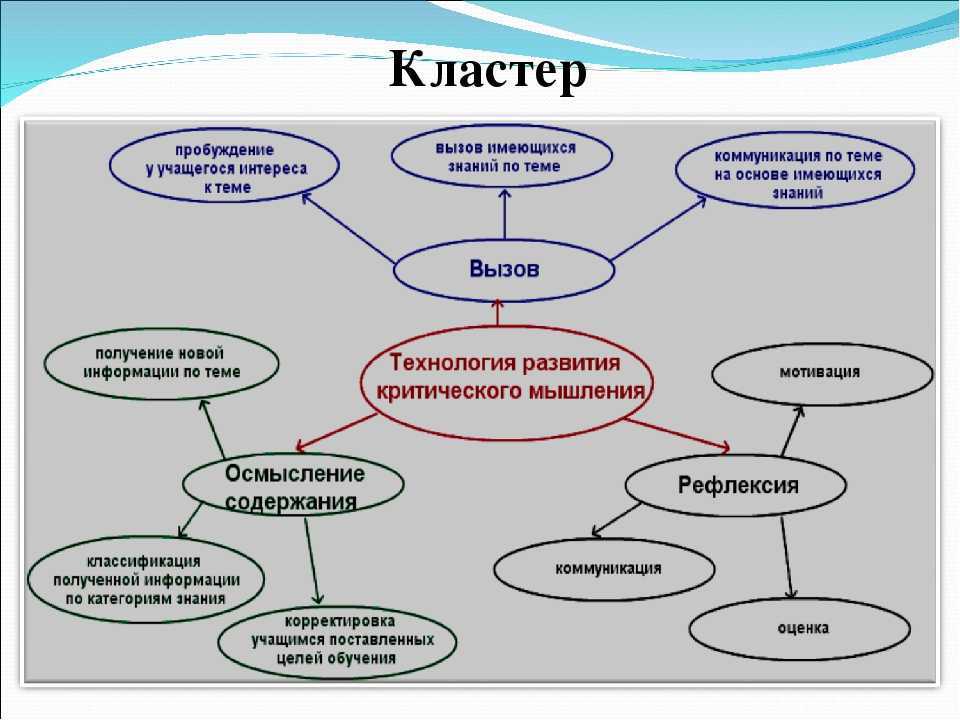 Он содержит примеры стратегий для разработки и оценки студенческой работы. В нем также представлена коллекция профилей преподавателей по учебной программе, которые уже обращаются к количественным рассуждениям в своих курсах.
Он содержит примеры стратегий для разработки и оценки студенческой работы. В нем также представлена коллекция профилей преподавателей по учебной программе, которые уже обращаются к количественным рассуждениям в своих курсах.
Преподавание количественных навыков в науках о Земле: этот веб-сайт предоставляет информацию по вопросам участвует в обучении количественным навыкам и методам и действиям для этого, а также дополнительным ресурсам и сообществу других преподавателей, которые все пытаются решить эту сложную задачу.
Инициатива Carleton’s Quantitative Inquiry, Reasoning, and Knowledge (QuIRK) — QuIRK — это мультидисциплинарная инициатива Карлтонского колледжа, направленная на решение количественных задач в рамках учебной программы . Инициатива проводит мероприятия кампуса и предоставляет ресурсы сообществу кампуса, а также широкой публике.
Преподавание с использованием электронных таблиц в рамках учебной программы. В этом проекте используются модули с короткими презентациями PowerPoint
Quantitative Writing — этот модуль является частью Starting Point и предоставляет информацию, учебные пособия и примеры , которые помогают использовать количественную запись в классе. Количественное письмо ставит перед учащимися задачу анализа и интерпретации чисел и данных посредством письма, чтобы придать смысл данным.
Видео прямых измерений — это короткие высококачественные видео реальных событий, которые учащиеся могут использовать для изучения и применения физических концепций
.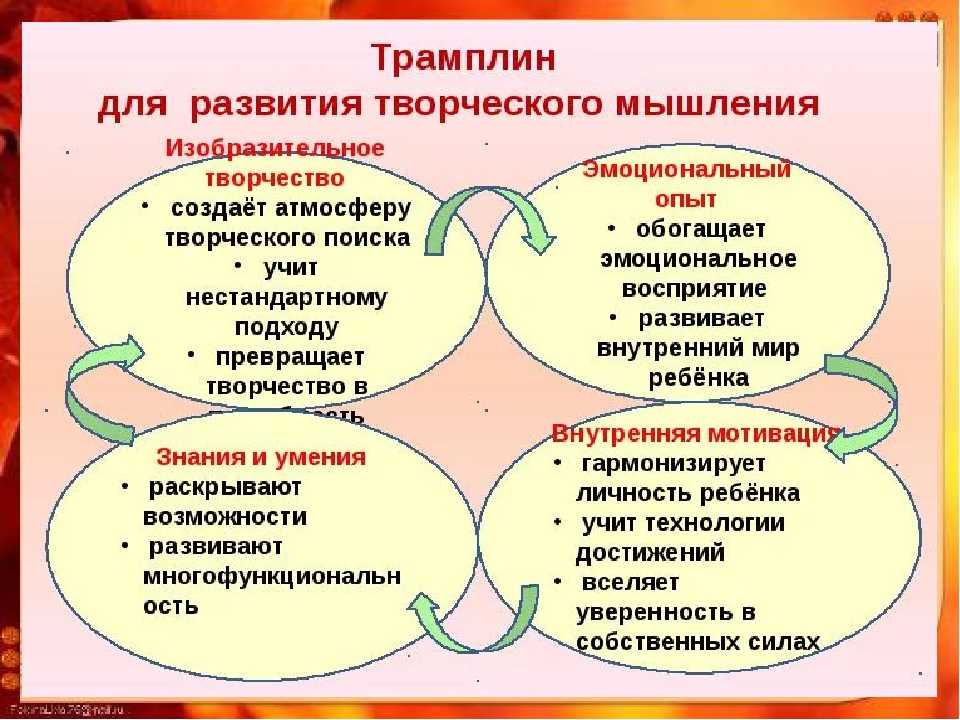 Видео можно использовать для лабораторных работ, домашних заданий, оценок или открытых задач. Несколько видео соединены с готовые занятия , которые интегрируют видео в учебную программу по вводной механике. Что отличает эти видео от других, так это то, что учащиеся могут измерять расстояния, время, углы и другие переменные прямо из видео, что позволяет проводить широкий спектр количественных и теоретических исследований.
Видео можно использовать для лабораторных работ, домашних заданий, оценок или открытых задач. Несколько видео соединены с готовые занятия , которые интегрируют видео в учебную программу по вводной механике. Что отличает эти видео от других, так это то, что учащиеся могут измерять расстояния, время, углы и другие переменные прямо из видео, что позволяет проводить широкий спектр количественных и теоретических исследований.Математика и статистические модели. Этот модуль предоставляет основную информацию о математических и статистических моделях, о том, как их можно использовать в классе, и предоставляет примеры действий , которые используют оба.
Математика, которая вам нужна. Эти модули охватывают  Они завершаются автоматически оцениваемым онлайн-тестом, который отправляется инструктору. Проект предназначен для того, чтобы дать студентам количественные знания , которые им нужны, всего до того, как им понадобится использовать их в параллельном курсе по геонаукам и включает модули предварительного и последующего тестирования, а также модули для самостоятельного изучения.
Они завершаются автоматически оцениваемым онлайн-тестом, который отправляется инструктору. Проект предназначен для того, чтобы дать студентам количественные знания , которые им нужны, всего до того, как им понадобится использовать их в параллельном курсе по геонаукам и включает модули предварительного и последующего тестирования, а также модули для самостоятельного изучения.
Преподавание количественных рассуждений с помощью новостей. Этот модуль из «Педагогики в действии» описывает, как можно использовать статьи из СМИ в качестве основного содержания курса, направленного на оттачивание способности учащихся критически обдумывать и анализировать количественную информацию .
Создание и проверка гипотез. Этот сайт, являющийся частью проекта CAUSE, предоставляет основную информацию о гипотезах и почему/как их можно использовать в классе как эффективный способ вовлечь учащихся и развить их мыслительные способности. Пример деятельности , в основном связанной со статистикой, также предоставляется.
Пример деятельности , в основном связанной со статистикой, также предоставляется.
Национальная вычислительная сеть (NNN) — эта организация предлагает своим членам сеть частных лиц, учреждений и корпораций, объединенных общей целью количественной грамотности для всех граждан. Посредством национальных встреч, семинаров преподавателей, исследовательских инициатив и обмена информацией NNN стремится укрепить потенциал нашей страны в количественных областях бизнеса, промышленности, образования и исследований во всех дисциплинах. Этот сайт включает в себя доступ к
Вводный курс по математическим вычислениям для высшего образования. Этот проект Городского университета Нью-Йорка (CUNY) Quantitative Reasoning Alliance направлен на содействие внедрению инструкций по количественному мышлению (QR) и оценке в курсы бакалавриата по учебной программе . В этом проекте также представлены передовой опыт и тематические исследования того, как QR преподается в ряде учебных заведений.
В этом проекте также представлены передовой опыт и тематические исследования того, как QR преподается в ряде учебных заведений.
Keyah Math. В рамках этого проекта была разработана серия разносторонних онлайн-мероприятий по математической науке о Земле с использованием природных и культурных ландшафтов юго-запада США в качестве контекста и обстановки. Эти упражнения на местах предназначены для улучшения любого курса бакалавриата по наукам о земле и могут представлять особый интерес для студентов и преподавателей, имеющих культурные связи с юго-западом , включая студентов и преподавателей из числа американских индейцев и латиноамериканцев.
Счетчик данных! Изучение общества в цифрах — DataCounts! это интерактивный веб-сайт , предназначенный для интеграции социальной статистики в школьную среду . Сайт предоставляет доступ к нескольким коллекциям данных и содержит набор учебных модулей, которые были созданы учителями по всей стране для интеграции данных социальных наук в свои классы.
Отправная точка: Преподавание и изучение экономики — этот сайт знакомит экономистов с инновационными стратегиями обучения развивался как в рамках экономической дисциплины, так и за ее пределами. Он предоставляет инструкторам инструменты , чтобы начать интеграцию и оценку этих стратегий обучения в своих классах , и способствует обмену инновациями в области обучения среди инструкторов.
Общий тест GRE Quantitative Reasoning Обзор
The GRE ® Общий тест
Один тест для аспирантов, школ бизнеса и права
Выберите шаг, чтобы узнать больше о вашем пути к общему тесту GRE ® .
Показатель количественного мышления общего теста GRE оценивает ваши:
- базовые математические навыки
- понимание элементарных математических понятий
- способность рассуждать количественно, а также моделировать и решать задачи количественными методами.

Покрываемые области контента
Некоторые вопросы количественного мышления задаются в реальных условиях, тогда как другие задаются в чисто математических условиях. Многие из вопросов представляют собой «словные задачи», которые необходимо перевести и смоделировать математически. Навыки, концепции и способности оцениваются в четырех областях содержания, указанных ниже.
- Темы арифметики, в том числе:
- свойства и типы целых чисел, такие как делимость, факторизация, простые числа, остатки, нечетные и четные целые числа
- арифметические операции, показатели степени и корни 90 128 таких понятий, как оценка, процент, отношение, скорость, абсолютное значение, числовая линия, десятичное представление и последовательность чисел 90 129
90 128 тем по алгебре, в том числе: 90 127 90 128 операций с показателями 90 129 - разложение на множители и упрощение алгебраических выражений
- отношения, функции, уравнения и неравенства
- решение линейных и квадратных уравнений и неравенств
- решение одновременных уравнений и неравенств
- составление уравнений для решения текстовых задач
- координатная геометрия, включая графики функций, уравнения и неравенства, точки пересечения и наклоны линий
- параллельные и перпендикулярные линии
- кругов
- треугольников, включая равнобедренные, равнобедренные и треугольники с углами 30°-60°-90°
- четырехугольники
- другие полигоны
- конгруэнтные и подобные фигуры
- Трехмерные фигуры
- район
- периметр
- объем
- теорема Пифагора
- измерение угла в градусах
Способность конструировать доказательства не проверяется.
- Темы анализа данных , включая:
- основные описательные статистические данные, такие как среднее значение, медиана, мода, диапазон, стандартное отклонение, межквартильный диапазон, квартили и процентили
- интерпретация данных в таблицах и графиках, таких как линейные графики, гистограммы, круговые диаграммы, ящичные диаграммы, диаграммы рассеяния и частотные распределения
- элементарная вероятность, такая как вероятности составных событий и независимых событий
- условная вероятность
- случайные величины и распределения вероятностей, включая нормальные распределения
- методов подсчета, таких как комбинации, перестановки и диаграммы Венна
Эти темы обычно преподаются на курсах алгебры в средней школе или на вводных курсах статистики.
Логическая статистика не проверена.
Содержание в этих областях включает математику и статистику средней школы на уровне, который обычно не выше второго курса алгебры. Он не включает тригонометрию, исчисление или другую математику более высокого уровня. В Math Review (PDF) предоставляется подробная информация о содержании меры количественного рассуждения.
Он не включает тригонометрию, исчисление или другую математику более высокого уровня. В Math Review (PDF) предоставляется подробная информация о содержании меры количественного рассуждения.
Символы, терминология, условные обозначения и допущения
Математические условные обозначения, терминология и условные обозначения, используемые в измерении количественного мышления, являются стандартными для старшей школы. Например, положительное направление числовой прямой — вправо, расстояния неотрицательны, а простые числа больше 1. Всякий раз, когда в вопросе используются нестандартные обозначения, они явно вводятся в вопросе.
Помимо условных обозначений, существуют некоторые важные предположения о числах и цифрах, которые перечислены в указаниях раздела «Количественное рассуждение»:
- Все используемые числа действительны.
- Предполагается, что все фигуры лежат в плоскости, если не указано иное.
- Геометрические фигуры, такие как линии, окружности, треугольники и четырехугольники, не обязательно изображаются в масштабе .
 Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:- линии, показанные прямыми, на самом деле являются прямыми
- точек на линии расположены в указанном порядке
- все геометрические объекты находятся в показанных относительных положениях
Ответы на вопросы с геометрическими фигурами следует основывать на геометрических рассуждениях, а не на оценке или сравнении величин визуально или путем измерения.
- Следующие нарисованы в масштабе . Вы можете считывать, оценивать или сравнивать количества и значения данных визуально или путем измерения:
- систем координат, таких как xy -плоскости и числовые линии
- графические представления данных, такие как гистограммы, круговые диаграммы и линейные графики
Чтобы узнать больше об соглашениях и допущениях, загрузите Mathematical Conventions (PDF).
Типы вопросов и наборы для интерпретации данных
Мера количественного рассуждения включает четыре типа вопросов:
- Вопросы количественного сравнения
- Вопросы с несколькими вариантами ответов — выберите один вариант ответа
- Вопросы с несколькими вариантами ответов — выберите один или несколько вариантов ответа
- Числовые вопросы ввода
Каждый вопрос появляется либо независимо как отдельный вопрос, либо как часть набора вопросов, который называется набором интерпретации данных. Все вопросы в наборе интерпретации данных основаны на одних и тех же данных, представленных в таблицах, графиках или других формах отображения данных.
В этих вопросах вам предлагается сравнить две величины — количество A и количество B — и затем определить, какое из следующих утверждений описывает сравнение.
- Количество A больше.
- Количество B больше.
- Обе величины равны.

- Отношение не может быть определено из предоставленной информации.
Советы по ответам на вопросы
- Ознакомьтесь с вариантами ответов . Вопросы количественного сравнения всегда имеют один и тот же вариант ответа, поэтому изучите их, особенно последний вариант: «Отношения не могут быть определены на основе предоставленной информации». Никогда не выбирайте этот последний вариант, если ясно, что значения двух величин могут быть определены вычислением. Кроме того, если вы определили, что одна величина больше другой, убедитесь, что вы тщательно выбрали соответствующий вариант и не меняете местами первые два варианта.
- Избегайте ненужных вычислений . Не тратьте время на ненужные вычисления для сравнения двух величин. Упростите, преобразуйте или оцените одну или обе заданные величины только по мере необходимости, чтобы сравнить их.
- Помните, что геометрические фигуры не обязательно рисуются в масштабе .
 Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены. Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?
Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены. Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов? - Вставьте числа . Если одна или обе величины являются алгебраическими выражениями, вы можете заменить переменные простыми числами и сравнить полученные величины в своем анализе. Рассмотрите все виды подходящих чисел, прежде чем давать ответ: например, ноль, положительные и отрицательные числа, маленькие и большие числа, дроби и десятичные дроби. Если вы видите, что количество A больше количества B в одном случае, а количество B больше количества A в другом случае, выберите «Отношение не может быть определено на основе предоставленной информации».
- Упростить сравнение . Если обе величины являются алгебраическими или арифметическими выражениями, и вы не можете легко увидеть взаимосвязь между ними, попробуйте упростить сравнение.
 Попробуйте выполнить пошаговое упрощение, которое аналогично шагам при решении уравнения для 90 263 x 90 264 или аналогичным шагам при определении того, что неравенство эквивалентно более простому неравенству Начните с настройки сравнения, включающего две величины:
Попробуйте выполнить пошаговое упрощение, которое аналогично шагам при решении уравнения для 90 263 x 90 264 или аналогичным шагам при определении того, что неравенство эквивалентно более простому неравенству Начните с настройки сравнения, включающего две величины:
, где это заполнитель, который может обозначать отношение больше (>), меньше (<) или равно (=), либо может обозначать тот факт, что отношение невозможно определить на основе предоставленной информации. Затем попытайтесь упростить сравнение, шаг за шагом, пока не сможете определить взаимосвязь между упрощенными величинами. Например, вы можете сделать вывод после последнего шага, который представляет собой равенство (=). Основываясь на этом выводе, вы, возможно, сможете сравнить количества A и B. Чтобы лучше понять эту стратегию, см. примеры вопросов 6–9..
В этих вопросах с несколькими вариантами ответов вам предлагается выбрать только один вариант ответа из списка из пяти вариантов.
Советы по ответу
- Используйте тот факт, что ответ есть .
 Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:
Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:- Внимательно перечитайте вопрос — возможно, вы упустили важную деталь или неверно истолковали какую-то информацию.
- Проверьте свои вычисления — возможно, вы допустили ошибку, например, неправильно набрали число на калькуляторе.
- Пересмотрите свой метод решения — у вас может быть изъян в рассуждениях.
- Просмотрите варианты ответов . В некоторых вопросах вас прямо спрашивают, какой из вариантов имеет определенное свойство. Возможно, вам придется рассмотреть каждый вариант отдельно или вы сможете увидеть взаимосвязь между вариантами, что поможет вам быстрее найти ответ. В других вопросах может быть полезно работать в обратном направлении от вариантов, например, заменяя варианты в уравнении или неравенстве, чтобы увидеть, какой из них работает. Однако будьте осторожны, так как этот метод может занять больше времени, чем использование рассуждений.

- Для вопросов, требующих приближения, просмотрите варианты ответов, чтобы увидеть, насколько близко требуется приближение . (Это может быть полезно и для других вопросов, так как поможет вам лучше понять, о чем идет речь.) Для некоторых вопросов вам, возможно, придется выполнить все вычисления точно и округлить только ваш окончательный ответ, чтобы получить необходимая степень точности. В других случаях оценки достаточно, и это поможет вам не тратить время на долгие вычисления.
В этих вопросах с несколькими вариантами ответов вам предлагается выбрать один или несколько вариантов ответа из списка вариантов. Вопрос может указывать или не указывать количество вариантов для выбора.
Советы по ответу
- Обратите внимание, просят ли вас указать определенное количество вариантов ответа или все варианты, которые применимы . В последнем случае обязательно рассмотрите все варианты, определите, какие из них правильные, и выберите все эти и только эти варианты.
 Обратите внимание, что правильный выбор может быть только один.
Обратите внимание, что правильный выбор может быть только один. - В некоторых вопросах, которые включают условия, ограничивающие возможные значения числовых вариантов ответа, может оказаться эффективным определить наименьшее и/или максимально возможное значение . Зная наименьшее и/или максимально возможное значение, вы сможете быстро определить все правильные варианты.
- Избегайте длинных вычислений, распознавая и продолжая числовые шаблоны .
Эти вопросы требуют, чтобы вы либо ввели свой ответ в виде целого числа или десятичной дроби в одно поле для ответа, либо в виде дроби в двух отдельных полях — одно для числителя и одно для знаменателя. Вы будете использовать компьютерную мышь и клавиатуру, чтобы ввести свой ответ.
Советы по ответу
- Убедитесь, что вы ответили на заданный вопрос . Поскольку нет вариантов ответов, которые могли бы вам помочь, внимательно прочитайте вопрос и убедитесь, что вы даете требуемый тип ответа.
 Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями.
Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями. - Если вас попросят округлить ответ, убедитесь, что округлили до требуемой степени точности . Например, если ответ 46,7 должен быть округлен до ближайшего целого числа, вам нужно ввести число 47. Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ.
- Изучите свой ответ, чтобы убедиться, что он разумен с учетом предоставленной информации . Вы можете использовать оценку или другой путь решения, чтобы перепроверить свой ответ.
Вопросы интерпретации данных сгруппированы вместе и относятся к одной и той же таблице, графику или другому представлению данных. Эти вопросы просят вас интерпретировать или анализировать данные. Типы вопросов могут быть с множественным выбором (оба типа) или числовым вводом.
Эти вопросы просят вас интерпретировать или анализировать данные. Типы вопросов могут быть с множественным выбором (оба типа) или числовым вводом.
Советы по ответу
- Кратко просмотрите презентацию данных, чтобы понять, о чем она, но не тратьте время на подробное изучение всей информации . Сосредоточьтесь на тех аспектах данных, которые необходимы для ответа на вопросы. Обратите внимание на:
- оси и шкалы графиков
- единицы измерения или порядки величины (например, миллиарды), указанные в заголовках, метках и легендах
- любые примечания, уточняющие данные
- Когда графические представления данных, такие как гистограммы и линейные графики, отображаются с помощью масштабов, вы должны считывать, оценивать или сравнивать количества визуально или путем измерения в соответствии с соответствующими масштабами . Например, используйте относительные размеры столбцов или секторов для сравнения величин, которые они представляют, но помните о ломаных шкалах и столбцах, которые не начинаются с 0.

- Отвечайте на вопросы только на основе представленных данных, повседневных фактов (таких как количество дней в году) и ваших знаний по математике . Не используйте специализированную информацию, которую вы можете вспомнить из других источников о конкретном контексте, на котором основаны вопросы, за исключением случаев, когда эта информация может быть получена из представленных данных.
Этапы решения проблем
В дополнение к советам по ответам в разделах типов вопросов выше, есть также некоторые общие шаги и стратегии решения проблем, которые вы можете использовать. Вопросы из измерения «Количественное мышление» требуют моделирования и решения проблем с использованием количественных или математических методов. Как правило, решение математической задачи состоит из трех основных шагов:
Внимательно прочитайте формулировку задачи, чтобы убедиться, что вы понимаете предоставленную информацию и задачу, которую вам предлагается решить.
- Некоторая информация может описывать определенные количества.
- Количественная информация может быть представлена словами или математическими выражениями, или их комбинацией.
- Вам может понадобиться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат.
- Другая информация может иметь форму формул, определений или условий, которым должны удовлетворять величины. Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Помимо понимания предоставленной вам информации, убедитесь, что вы понимаете, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные величины необходимо найти? В какой форме они должны быть выражены?
Решение математической задачи требует большего, чем понимание описания задачи (количество, данные, условия, неизвестные и все другие математические факты, связанные с задачей). Это также требует определения какие математические факты использовать и когда и как использовать эти факты для разработки решения задачи. Это требует стратегии.
Это также требует определения какие математические факты использовать и когда и как использовать эти факты для разработки решения задачи. Это требует стратегии.
Математические задачи решаются с использованием самых разных стратегий, и могут быть разные способы решения данной задачи. Разработайте репертуар стратегий решения проблем и понимание того, какие стратегии, вероятно, будут работать лучше всего при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большой работе без получения правильного решения.
После того, как вы определите стратегию, выполните ее. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибку в своем решении. Сохраняйте гибкий и открытый образ мышления. Если вы проверяете свое решение и не можете найти ошибку, или если ваша стратегия решения просто не работает, поищите другую стратегию.
Когда вы получите ответ, убедитесь, что он разумен и корректен с точки зрения вычислений.
- Вы ответили на заданный вопрос?
- Является ли ваш ответ обоснованным в контексте вопроса? Проверить правильность ответа можно так же просто, как вспомнить основной математический факт и проверить, согласуется ли ваш ответ с этим фактом. Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. Возможно, вы сможете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
- Вы допустили вычислительную ошибку при получении ответа или ошибку при вводе ключа с помощью калькулятора? Проверьте наличие ошибок на каждом этапе вашего решения. Или вы можете напрямую проверить правильность вашего решения. Например, если вы решаете уравнение относительно x, подставьте свой ответ в уравнение, чтобы убедиться, что он правильный.

Стратегии
Не существует установленных правил, применимых ко всем математическим задачам, для определения наилучшей стратегии. Способность определить стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Загрузите примеры вопросов, чтобы получить список из 14 полезных стратегий, которые вы можете использовать, а также один или два примера вопросов, которые иллюстрируют, как использовать каждую стратегию.
Скачать PDF
Использование калькулятора
Вам предоставляется базовый экранный калькулятор для меры количественного рассуждения. Иногда вычисления, которые вам нужно сделать, чтобы ответить на вопрос в показателе количественного рассуждения, требуют много времени, например, деление в длинную сторону, или они включают в себя квадратные корни. Хотя калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор дает результаты, которые дополняют, но не заменяют ваши знания математики. Вам нужно будет использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как результаты можно использовать для ответа на вопрос.
Вам нужно будет использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как результаты можно использовать для ответа на вопрос.
Вот некоторые общие рекомендации по использованию калькулятора в измерении количественного мышления:
- Большинство вопросов не требуют сложных вычислений, поэтому не используйте калькулятор только потому, что он доступен.
- Используйте его для вычислений, которые, как вы знаете, утомительны, таких как деление в длинную сторону, извлечение квадратных корней, а также сложение, вычитание или умножение чисел, состоящих из нескольких цифр.
- Не используйте его для простых вычислений, которые быстрее выполнить в уме, таких как и
- Не используйте его для введения десятичных знаков, если вас просят дать ответ в виде дроби.
- Возможно, вы сможете быстрее ответить на некоторые вопросы, рассуждая и оценивая, чем используя калькулятор.
- Если вы пользуетесь калькулятором, оцените ответ заранее, чтобы вы могли определить, является ли ответ калькулятора «приблизительным».

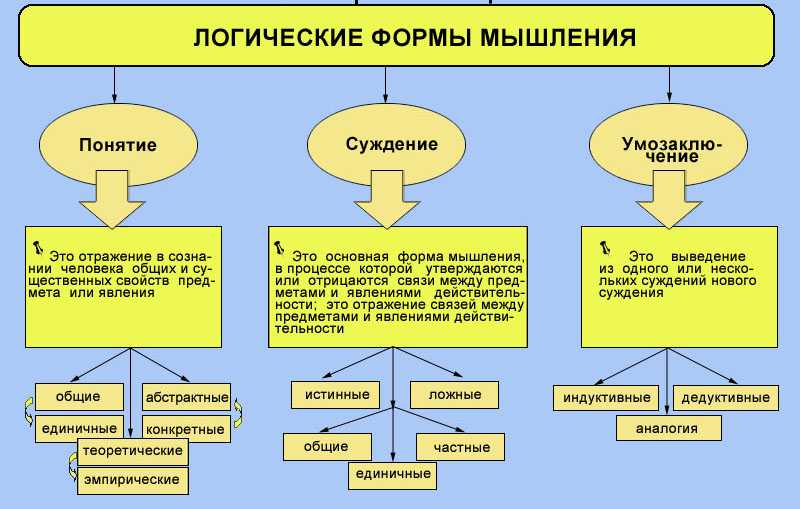 Дайте еще такого, пожалуйста, очень интересно.
Дайте еще такого, пожалуйста, очень интересно.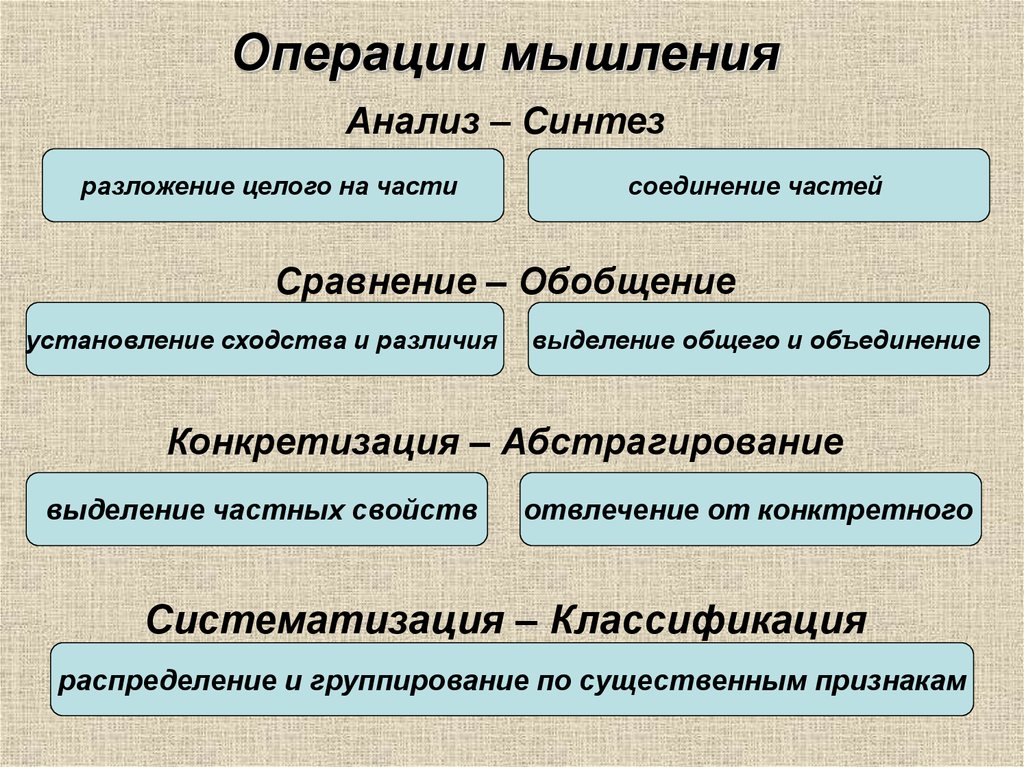

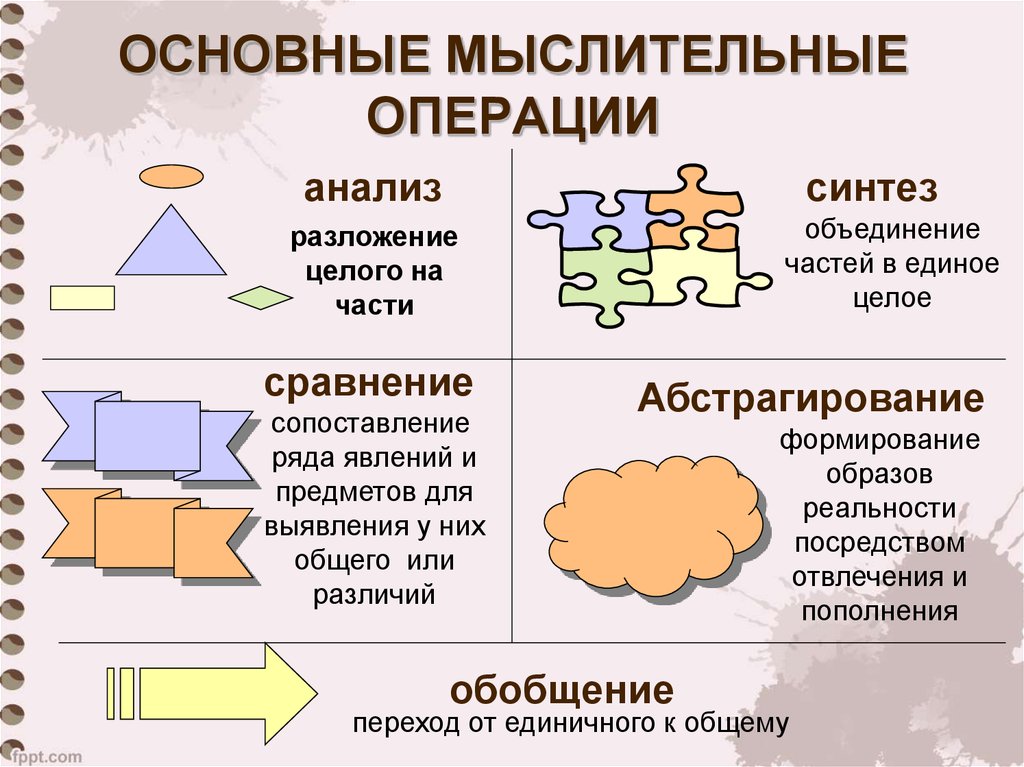 Причем сильно. Средний человек плавает даже в задачах начальной школы на одно-два действия. А средний человек с «высшим образованием» недалеко ушел от просто среднего человека.
Причем сильно. Средний человек плавает даже в задачах начальной школы на одно-два действия. А средний человек с «высшим образованием» недалеко ушел от просто среднего человека.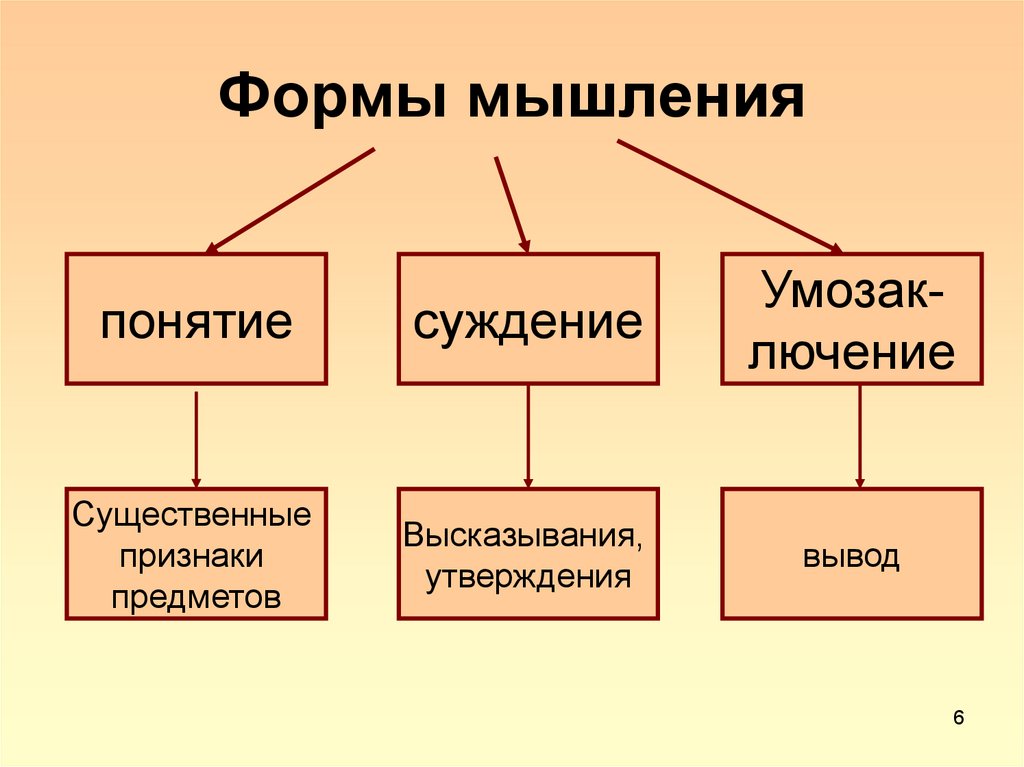

 Возможный механизм ошибки: Что-то связанное с 6+1=7, нужно умножить на два. Видим 70, резко отвечаем 14.
Возможный механизм ошибки: Что-то связанное с 6+1=7, нужно умножить на два. Видим 70, резко отвечаем 14.
 Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
 Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены. Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?
Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены. Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов? Попробуйте выполнить пошаговое упрощение, которое аналогично шагам при решении уравнения для 90 263 x 90 264 или аналогичным шагам при определении того, что неравенство эквивалентно более простому неравенству Начните с настройки сравнения, включающего две величины:
Попробуйте выполнить пошаговое упрощение, которое аналогично шагам при решении уравнения для 90 263 x 90 264 или аналогичным шагам при определении того, что неравенство эквивалентно более простому неравенству Начните с настройки сравнения, включающего две величины:  Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:
Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:
 Обратите внимание, что правильный выбор может быть только один.
Обратите внимание, что правильный выбор может быть только один. Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями.
Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями.