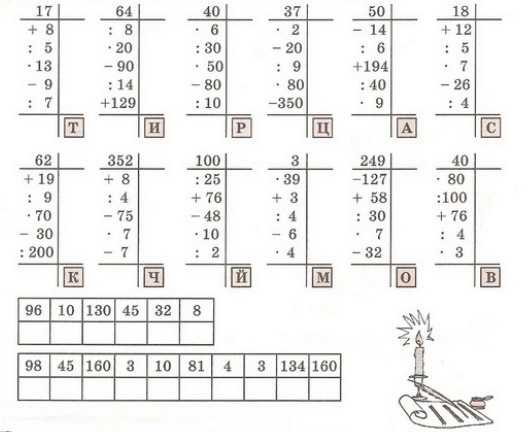
Примеры на деление. Математика 4 класс.
Примеры на деление. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 9520 : 8 = 1190 | 21000 : 210 = 100 | 5500 : 11 = 500 | 22000 : 20 = 1100 | 6860 : 7 = 980 |
| 78400 : 56 = 1400 | 228000 : 38 = 6000 | 905000 : 50 = 18100 | 844000 : 20 = 42200 | 18000 : 450 = 40 |
| 2610 : 9 = 290 | 29600 : 740 = 40 | 2400 : 48 = 50 | 80000 : 80 = 1000 | 66300 : 30 = 2210 |
| 50400 : 63 = 800 | 94500 : 35 = 2700 | 264000 : 300 = 880 | 84600 : 600 = 141 | 68000 : 680 = 100 |
| 8720 : 4 = 2180 | 32000 : 400 = 80 | 51700 : 47 = 1100 | 102000 : 600 = 170 | 10000 : 200 = 50 |
| 98800 : 260 = 380 | 9880 : 26 = 380 | 282000 : 60 = 4700 | 692000 : 40 = 17300 | 426000 : 71 = 6000 |
| 76300 : 700 = 109 | 81600 : 510 = 160 | 8400 : 70 = 120 | 60900 : 70 = 870 | 136000 : 80 = 1700 |
| 777000 : 37 = 21000 | 84800 : 800 = 106 | 450000 : 900 = 500 | 72000 : 200 = 360 | |
| 83200 : 400 = 208 | 6120 : 9 = 680 | 41800 : 380 = 110 | 68400 : 6 = 11400 | 252000 : 900 = 280 |
| 69000 : 50 = 1380 | 660000 : 550 = 1200 | 48000 : 96 = 500 | 43400 : 700 = 62 | 108000 : 300 = 360 |
| 671000 : 61 = 11000 | 8520 : 2 = 4260 | 89000 : 89 = 1000 | 79200 : 880 = 90 | 312000 : 80 = 3900 |
| 390000 : 300 = 1300 | 7700 : 77 = 100 | 188000 : 940 = 200 | 405000 : 500 = 810 | 436000 : 400 = 1090 |
| 600000 : 24 = 25000 | 7400 : 200 = 37 | 884000 : 17 = 52000 | 498000 : 30 = 16600 | 74200 : 200 = 371 |
| 7200 : 72 = 100 | 940 : 94 = 10 | 83200 : 800 = 104 | 3200 : 8 = 400 | 66300 : 17 = 3900 |
| 5820 : 6 = 970 | 630000 : 900 = 700 | 910000 : 70 = 13000 | 98000 : 50 = 1960 | 1280 : 8 = 160 |
| 83000 : 830 = 100 | 15000 : 75 = 200 | 540000 : 900 = 600 | 310000 : 500 = 620 | 120000 : 10 = 12000 |
| 80000 : 80 = 1000 | 52800 : 44 = 1200 | 636000 : 40 = 15900 | 2790 : 9 = 310 | |
| 297000 : 270 = 1100 | 969000 : 300 = 3230 | 67000 : 67 = 1000 | 86000 : 40 = 2150 | 894000 : 30 = 29800 |
| 332000 : 20 = 16600 | 583000 : 530 = 1100 | 882000 : 980 = 900 | 148000 : 20 = 7400 | 9325 : 25 = 373 |
| 7790 : 41 = 190 | 350000 : 250 = 1400 | 12600 : 60 = 210 | 48000 : 600 = 80 | 2100 : 70 = 30 |
| 432000 : 540 = 800 | 90300 : 300 = 301 | 26500 : 500 = 53 | 390 : 39 = 10 | 52600 : 200 = 263 |
| 64400 : 23 = 2800 | 19200 : 960 = 20 | 78000 : 200 = 390 | 552000 : 200 = 2760 | 65000 : 95 = 67000 |
| 61000 : 610 = 100 | 3180 : 6 = 530 | 696000 : 400 = 1740 | 7100 : 71 = 100 | 738000 : 60 = 12300 |
| 98000 : 70 = 1400 | 385000 : 11 = 35000 | 1120 : 7 = 160 | 89100 : 90 = 990 | 36400 : 91 = 400 |
| 4000 : 200 = 20 | 8900 : 89 = 100 | 98000 : 50 = 1960 | 6650 : 95 = 70 | 1500 : 2 = 750 |
| 546000 : 91 = 6000 | 55300 : 7 = 7900 | 10000 : 20 = 500 | 328000 : 40 = 8200 | 192000 : 960 = 200 |
| 33000 : 110 = 300 | 540000 : 600 = 900 | 952000 : 400 = 2380 | 39600 : 44 = 900 | 860 : 2 = 430 |
| 18000 : 150 = 120 | 18200 : 26 = 700 | 4500 : 5 = 900 | 6060 : 2 = 3030 | 408000 : 51 = 8000 |
| 53700 : 30 = 1790 | 54900 : 900 = 61 | 666000 : 370 = 1800 | 71200 : 400 = 178 | 4950 : 55 = 90 |
| 48800 : 61 = 800 | 203000 : 70 = 2900 | 450 : 9 = 50 | 170000 : 17 = 10000 | 81900 : 90 = 910 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме.
Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем.
В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.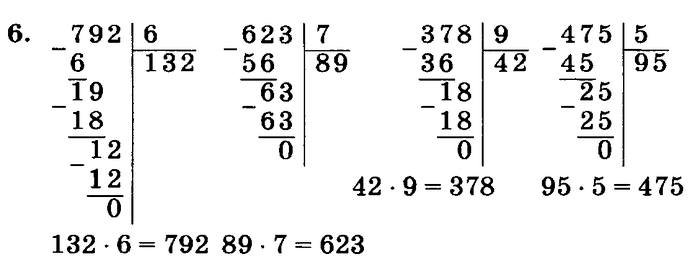
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления.
Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0. В итоге отмечаем новое рабочее число — 20.
Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:
В самой нижней строчке записываем число 0. Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбикРазделим натуральное число 7136 на натуральное число 9.
Запишем:
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбикРазделим число 7042035 на 7.
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число.
Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбикРазделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.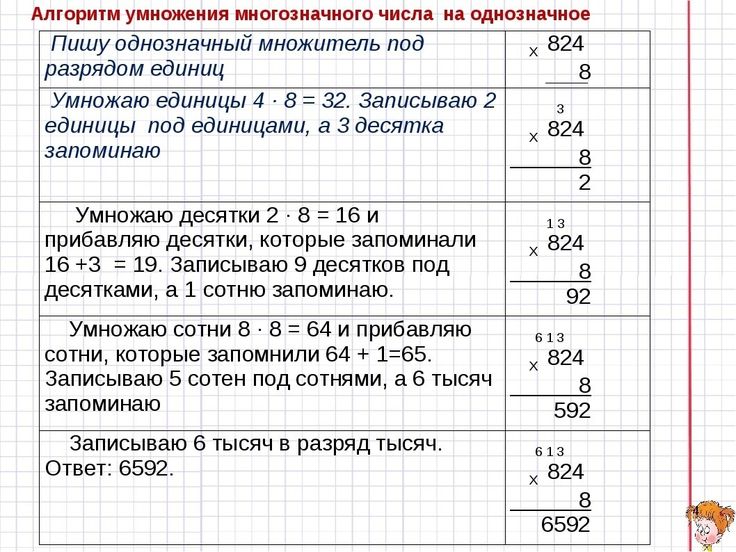
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбикРазделим натуральное число 238079 на 34.
Ответ: 7002
Стратегии разделения для 4 и 5 классов
Прослушать эту статью
Оценить эту публикацию
В этой статье обсуждаются три стратегии разделения. Кроме того, вы найдете решенные примеры с пояснениями и ссылками на рабочие листы для дополнительной практики или оценки.
Что такое подразделение?
Одной из четырех основных математических операций, наряду со сложением, вычитанием и умножением, является деление.
Деление — это процесс разделения большей группы на более мелкие таким образом, чтобы каждая группа содержала равное количество элементов.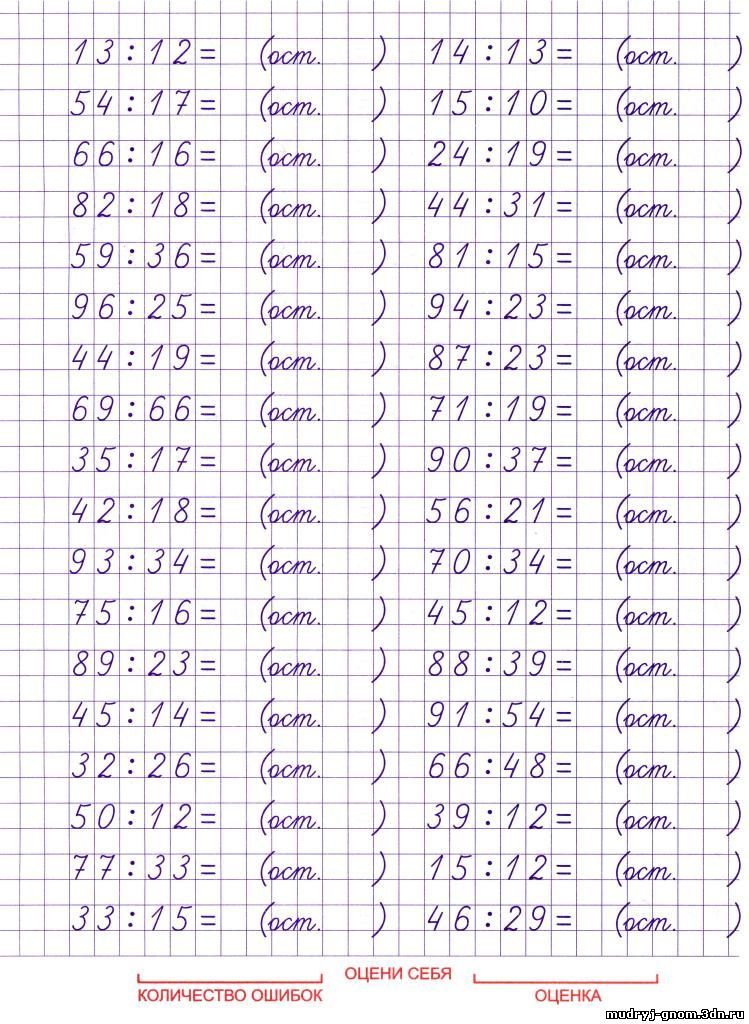
Математики используют эту операцию для группировки и равномерного распределения ресурсов.
Деление обратное умножению. При делении чисел мы разбиваем большее число на меньшее так, чтобы произведение меньшего числа было равно большему числу.
Например, 10 ÷ 2 = 5. Мы можем выразить это как факт умножения 2 x 5 = 10,
Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .
Имя *
Адрес электронной почты *
Символы деления
Мы можем представить деление двух чисел одним из двух основных символов деления ( ÷ и /).
Например, 10 ÷ 2 = 5, а 10/2 = 5.
Математический символ, который выглядит как небольшая горизонтальная линия с точками над и под ней, чаще всего используется для обозначения деления.
Части деления
Задача на деление состоит из следующих четырех компонентов: делимое, делитель, частное и остаток.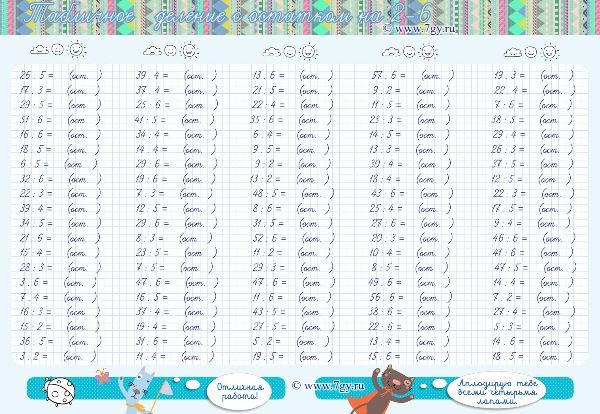
В уравнении деления 458 ÷ 3 = 152 R2 ;
- делимое (458) число, которое нужно разделить (первое число слева)
- делитель (3) это число, на которое делим делимое (второе число после знака деления)
- частное (152) — ответ, полученный после выполнения деления (число справа после знака равенства)
- остаток (2) это оставшееся значение, которое меньше делителя (числа, присоединенного к частному)
Стратегии деления
Мы можем использовать таблицу умножения для деления небольших чисел.
Например, чтобы решить 10 ÷ 2, нам нужно только определить, что мы должны умножить на 2, чтобы получить 10 в качестве ответа.
Ясно, что 2 × 5 = 10, поэтому 10 ÷ 2 = 5.
Однако при делении больших чисел практически невозможно использовать этот подход.
Поэтому мы должны придумать альтернативные стратегии для использования при делении больших чисел.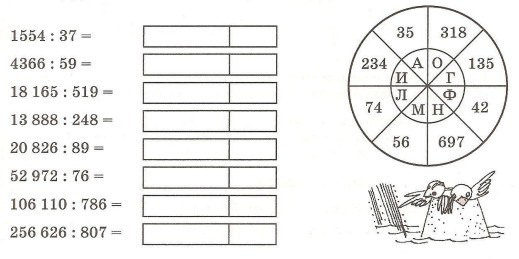
Некоторые из таких стратегий разделения включают;
- Длинная часть
- Разделение на частное
- Зона модельного подразделения
Использование длинного деления в качестве стратегии деления.
Длинное деление — это метод деления больших чисел, который разбивает задачу на несколько шагов, выполняемых в определенном порядке.
Мы сможем делить числа любой длины, как только освоим этапы деления в длинное число.
Как разделить, используя метод деления в длину?
Следуя описанным здесь шагам, вы можете легко разделить, используя деление в большую сторону.
- Разделить
- Умножить
- Вычесть
- Сбить
- Повторить процесс
Чтобы лучше понять длинное деление, давайте попробуем это на примере 458 ÷ 3 .
Шаг 1 – Разделить
Составьте уравнение.- Нарисуйте символ длинного деления ⟌
- Напишите делитель (3) слева вне символа, а делимое (458) справа под символом деления.
- Работая слева направо, определите, сколько раз делитель может входить в первую цифру делимого, не превышая ее.
- В нашем примере вам нужно знать, сколько раз 3 входит в 4, что равно 1.
- Если делитель больше первой цифры ( 138 ÷ 3) , определите, сколько раз делитель входит в первые две цифры делимого, не превышая его.
- В этом случае вам нужно знать, сколько раз 3 входит в число 13, то есть 4.
- Поместите количество раз, когда делитель входит в первую цифру (или первые две цифры) делимого сверху символа деления над соответствующей цифрой.
- Длинное деление требует, чтобы числовые столбцы оставались правильно выровненными.
- В 458 ÷ 3 вы должны поставить 1 над 4, так как мы смотрим, сколько раз 3 входит в 4.
- В 138÷3 вы должны поставить 4 над 3, так как мы смотрим, сколько раз 3 входит в 13.
Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .
Имя *
Адрес электронной почты *
Шаг 2 – Умножение
Умножение и запись произведения.- Умножьте делитель на цифру частного, которую вы только что написали над делимым. (3 х 1 = 3 и 3 х 4 = 12).
- Запишите результат умножения под делимым.
- В первом примере напишите 3 под 4 и 12 под 13 во втором примере, следя за тем, чтобы числа были выровнены.
Шаг 3 – Вычесть
Вычесть произведение.
- Нарисуйте линию под результатом умножения.
- Вычтите число (произведение умножения) из цифр делимого непосредственно над ним.
- Запишите результат под только что проведенной линией.
- В примерах вычтите 3 из 4, чтобы получить 1, и 12 из 13, чтобы получить 1.
Шаг 4 – Уменьшение
Уменьшение следующей цифры.- Поскольку делитель не может входить в результат операции вычитания, необходимо опустить следующую цифру делимого (если она есть).
- В первом примере, поскольку 3 не может войти в 1, не превысив его, вам нужно убрать 5 из 458 и поместить его после 1, получив 15, в которое может войти 3.
Шаг 5. Повторите процесс
Повторите весь процесс.- Разделите новое число на делитель и запишите результат над делимым как следующую цифру частного.
- В этом примере определите, сколько раз 3 может составить 15. Запишите это число (5) как следующую цифру частного перед делимым.
- Затем умножьте 3 на 5 и вычтите результат (15) из 15.
- Если в делимом больше цифр, повторяйте этот процесс до тех пор, пока не проработаете их все (пока не получите ноль или число меньше делителя).
Запишите это число (5) как следующую цифру частного перед делимым.- Запишите, есть ли остаток, т. е. указание того, сколько осталось после того, как вы завершили свое деление.
- В этом примере остаток будет равен 2, потому что 3 не может перейти в 2, и больше нет цифр, которые нужно записывать.
- Поместите остаток после частного с буквой «R» перед ним. В примере ответ будет выражен как «152 R2».
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
Те же шаги можно выполнить для деления на двузначные делители.
Здесь вы узнаете, сколько раз двузначный делитель входит в первые две или три цифры делимого.
Это точно так же, как найти, сколько раз однозначный делитель входит в первые одну или две цифры делимого, как обсуждалось в предыдущих шагах.
Использование неполных частных в качестве стратегии деления.
Деление с частичными частными отличается от стандартного метода.
Метод неполных частных побуждает учащихся разбивать вопросы на деление на «более понятные» части.
Для решения простых задач на деление в подходе с частичными частными используется повторное вычитание.
Как разделить с помощью метода неполных частных?
Выполняя шаги, описанные здесь, вы можете легко делить, используя метод частичных частных.
- Найдите и вычтите кратное
- Повторите процесс
- Сложить неполные частные
Чтобы лучше понять деление частичных частных, давайте попробуем это на примере 458 ÷ 3 .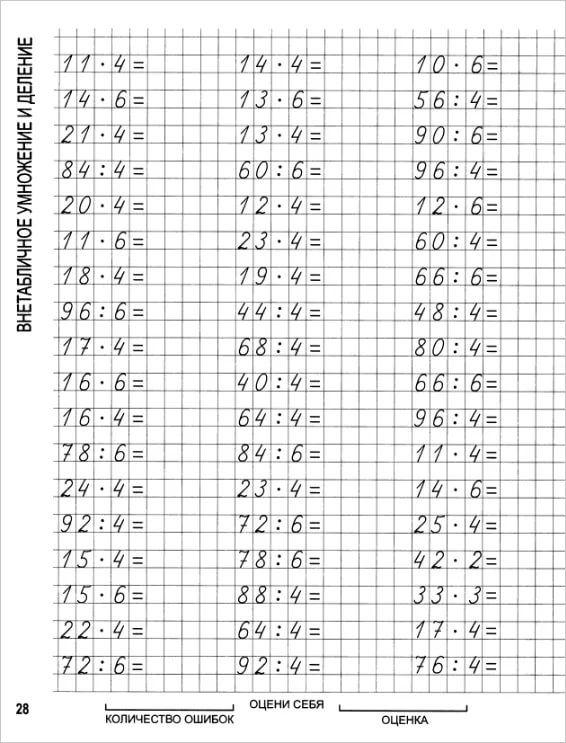
Шаг 1. Найдите и вычтите простое кратное.
- Для этого умножьте делитель на более удобное число, такое как 100, 10, 5, 2 и т. д., чтобы получить простое кратное делителя. В примере 3 х 100 = 300.
- Кратность делителя должна быть как можно ближе к делимому (меньше или равно делимому).
- Множитель или число, на которое умножается делитель, является неполным частным.
- Запишите произведение или кратное (300) под делимым (458) и частичным частным (100) справа.
- Нарисуйте линию и вычтите кратное из делимого (458 – 300 = 158)
Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .
Имя *
Адрес электронной почты *
Шаг 2.
Повторите процесс Найдите еще одно кратное делителю .- Вычтите кратное из разности (158) и запишите частичное частное.
- Продолжайте умножать и вычитать, пока разница не станет меньше делителя или равна 0.
- Если разница меньше делителя, то эта разница является остатком .
Шаг 3. Сложите неполные частные
Сложите неполные частные, чтобы найти окончательное частное.- Сложите частичные частные справа.
- Если есть остаток, присоедините его к конечному частному, чтобы получить ответ на деление. В примере 458 ÷ 3 = 152 R2
Те же шаги можно использовать для деления на две цифры. Найдите и вычтите кратное двузначного делителя из делимого так же, как вы сделали с однозначным делителем.
Длинному делению не хватает гибкости деления на частичные частные.
Длинное деление должно быть выполнено точно, но с частичными частными можно просто несколько раз вычесть из делимого кратное делителю и все равно получить правильный ответ.
Вы можете использовать метод неполных частных, чтобы усилить разрядное значение и концепцию деления как многократного вычитания.
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
Продажа Товар в продаже
9,00 $
В корзину
Добавить в список желаний
Использование модели района в качестве стратегии разделения.
Модель области — отличный способ для визуалов понять и осмыслить деление, а также улучшить их чувство числа.
Метод модели площади, как и метод частных частных, использует многократное вычитание.
Кроме того, площадная модель представляет собой способ выражения деления с помощью прямоугольников.
Длина и ширина прямоугольника определяются частичными частными и делителем.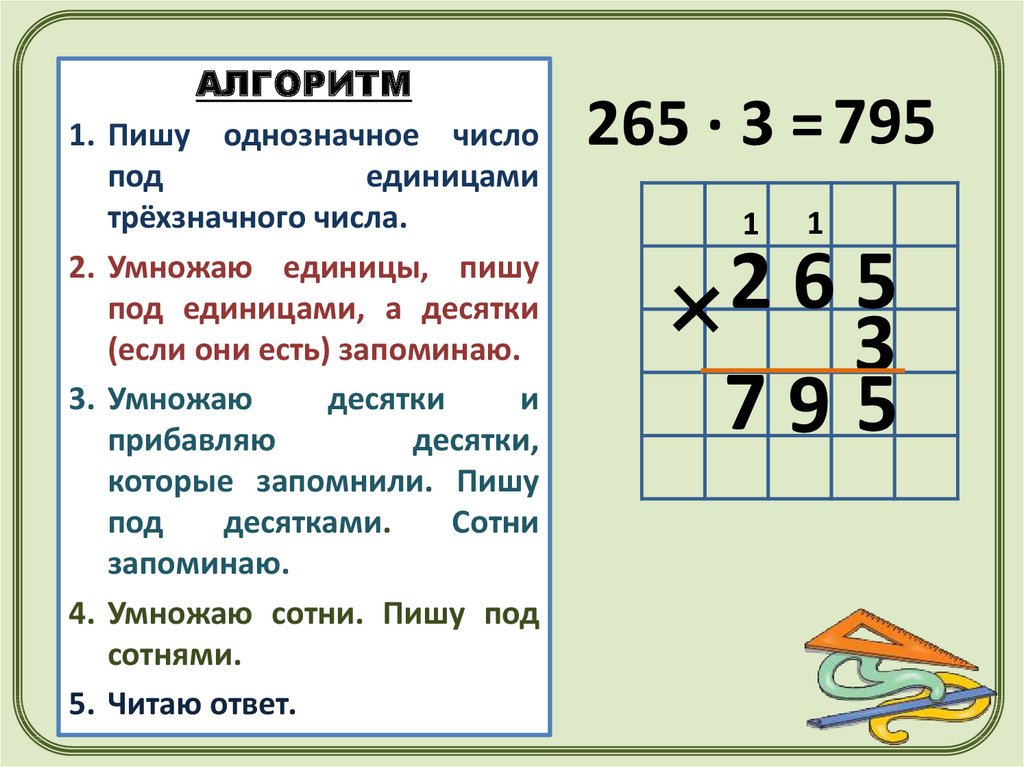
В результате в прямоугольнике будет столько же столбцов, сколько и неполных частных.
Как разделить с помощью метода модели площади?
Метод модели площади подобен методу частных частных по своим шагам, с той лишь разницей, что проблема представлена.
- Найти и вычесть простое кратное
- Повторить процесс
- Сложение частичных коэффициентов
Чтобы лучше понять деление модели области, давайте попробуем это на примере 458 ÷ 3 .
Шаг 1 – Найдите и вычтите простое кратное
Поставьте задачу (458 ÷ 3).- Нарисуйте прямоугольник и разделите его на 2, 3, … столбца (которых будет столько, сколько неполных частных).
- Запишите делитель (3) слева за пределами прямоугольника и делимое (458) внутри первого столбца, оставив достаточно места под числом.
- Для этого умножьте делитель на более удобное число, такое как 100, 10, 5, 2 и т. д., чтобы получить простое кратное делителя. В примере 3 х 100 = 300.
- Кратность делителя должна быть как можно ближе к делимому (меньше или равно делимому).
- Множитель или число, на которое умножается делитель, является неполным частным.
- Запишите частичное частное (100) сверху первого столбца и кратное (300) под делимым (458) внутри столбца.
- Нарисуйте линию и вычтите кратное из делимого (458 – 300 = 158)
д., чтобы получить простое кратное делителя. В примере 3 х 100 = 300.Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .
Имя *
Адрес электронной почты *
Шаг 2. Повторите процесс
Запишите разницу между делимым и кратным (158) во второй колонке.- Найдите еще одно кратное делителю, вычтите из разницы и запишите неполное частное сверху второго столбца.
- Продолжайте умножать и вычитать, пока разница не станет меньше делителя или не станет равной 0.
- Если разница меньше делителя, то эта разница является остатком.
Шаг 3. Сложите неполные частные
Сложите неполные частные, чтобы найти окончательное частное.- Сложите числа в верхней части столбцов (частичные частные), чтобы найти окончательное частное.
- Если есть остаток, присоедините его к конечному частному, чтобы получить ответ на деление. В примере 458 ÷ 3 = 152 R2
Те же шаги можно использовать для деления на две цифры. Найдите и вычтите кратное двузначного делителя из делимого так же, как вы сделали с однозначным делителем.
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
$ 3,75
В корзину
Добавить в список желаний
Продажа Товар в продаже
9,00 $
В корзину
Добавить в список желаний
В любом факте деления делимое всегда равно произведению делителя и частного, прибавленного к остатку.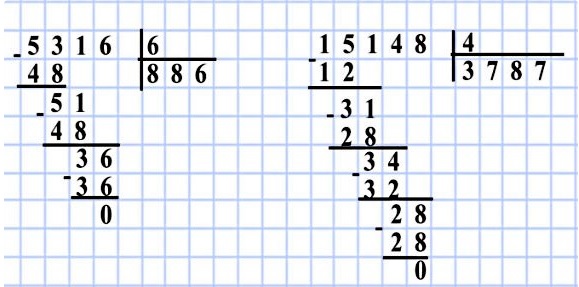
Таким образом, Дивиденд = (Делитель × Частное) + Остаток .
Приведенная выше формула помогает нам проверить значения частного и остатка, полученные после выполнения деления.
Мы можем подставить значения частного, остатка и делителя в уравнение, чтобы проверить, совпадает ли результат с делимым.
Если результат одинаковый, мы правильно выполнили шаги деления. Если нет, то в наших расчетах возникла проблема, которую необходимо исправить.
Проверим ответ нашей задачи на деление: 458 ÷ 3 = 152 R2
Дивиденд = (Делитель × Частное) + Остаток
458 = (3 × 152) + 2
458 = 456 + 2
, таким образом, 458 = 458
Результат тот же, следовательно, проверено, что мы правильно решили задачу деления.
Заключение
Как и другие математические операции, деление — это жизненный навык, которым дети или учащиеся должны овладеть в раннем возрасте, чтобы решать некоторые жизненные задачи.