Математика домики состав числа: Домики «Состав числа» от 1 до 10, от 11 до 20

Числовые домики для дошкольников

25.01.2022

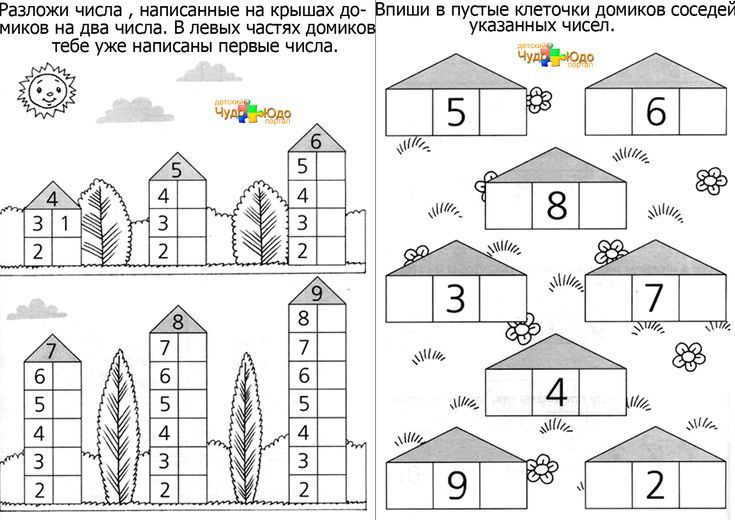
Первоклассники начинают изучать сложение и вычитание только после того, как изучат состав числа. Чтобы малыши лучше усвоили тему, специалисты рекомендуют использовать всевозможные наглядные учебные материалы – таблицы, иллюстрации, схемы. В числе самых наглядных – числовые домики.

Содержание:

• Принцип работы пособия
• Как заниматься с арифметическими домиками?

Принцип работы пособия

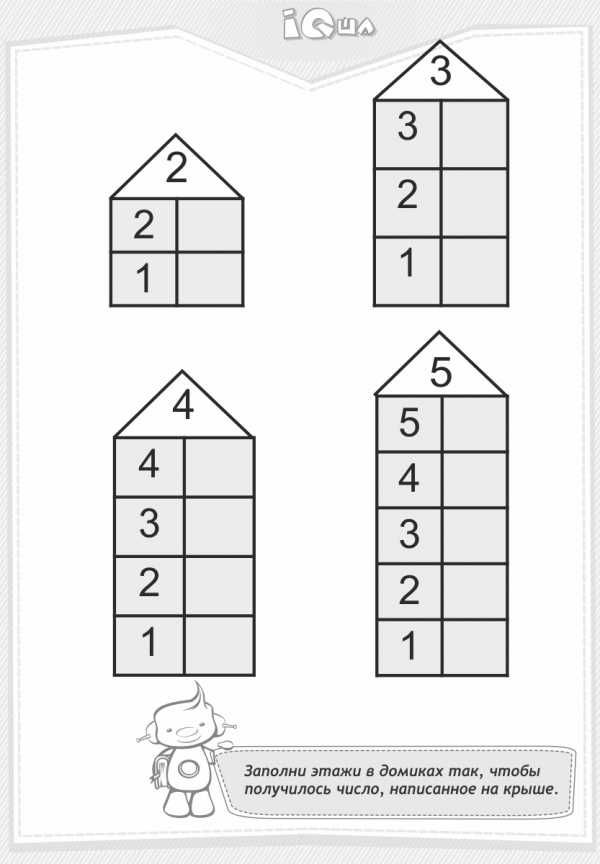
Обучаясь по картинкам-домикам, ребенок легко запоминает состав однозначных чисел. Например, в домике числа 5 два этажа. На этажах живут соседи-числа, их нужно запомнить: 4 и 1, 3 и 2. Соседей разрешается менять местами, но не этажами. Самый крупный домик, в котором много соседей, – дом числа десять. В домике пять этажей, на которых живут 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5. Запомнив все их, ребенок легко может вычитать из десяти, к примеру, семь и не ошибаться при этом.

Чтобы закрепить полученные знания, нужно заниматься по таким же карточкам, но где в домиках пустуют окошки. В них ребенку предлагается вписать нужного соседа именно этого этажа. К примеру, в домике 7 рядом с соседом 3 может жить только число 4.

С помощью арифметических домиков малыш хорошо усваивает состав любого числа. Также у него развивается навык быстрого устного счета. Пособие можно сделать из картона самостоятельно или найти в математических учебниках, в интернете.

Как заниматься с арифметическими домиками?

Берем пустой дом, на крыше которого указано число от 2 до 10 – столько людей проживает в этом здании. Стоит взять за правило, что на первом этаже в квартире №1 в любом доме живет всего один человек. Пусть ребенок догадается, что, например, для домика числа 6 в квартире №2 находятся пять жильцов.

По этому алгоритму ребенок должен «заселить» все квартиры домика, меняя начальное количество жильцов на каждом этаже.

Он должен получить на втором этаже два и четыре жильца, на третьем – три и три, на четвертом – шесть и ноль.

Можно подсказать ребенку, что любое число состоит из единицы и предыдущей по порядку цифры. Таким образом, первый этаж домика, например, семерки, всегда будет заселен одним и шестью жильцами.

Задание можно усложнить – «строить» домики для чисел больше десятки.

Читайте также:

Индивидуальные занятия ментальной арифметикой для детей

Курсы ментальной арифметики. Развиваем интеллект и математические способности! Детям от 4 лет! Индивидуально. Онлайн. В удобное время.

Как помочь ребенку выбрать будущую профессию

Не все подростки могут своевременно определиться с выбором будущей профессии.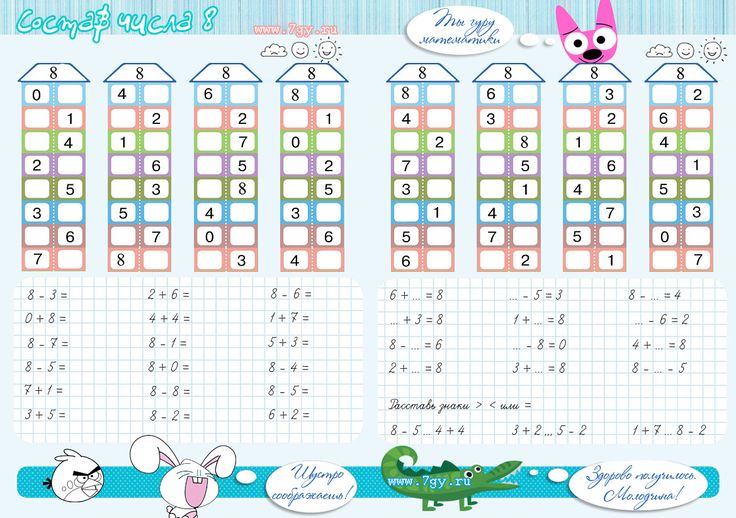 Родители в силах помочь своему ребенку. Важно делать это деликатно, ненавязчиво, отойти от распространенных стереотипов.

Игры Воскобовича для дошкольников

Вячеслав Воскобович разработал десятки увлекательных игровых пособий для дошкольников, которые способствуют всестороннему развитию ребенка. Методика Воскобовича опирается на детскую фантазию , игры сопровождаются сказочным сюжетом.

Как правильно объяснить дошкольнику состав числа

В первом классе ученик обязательно изучает состав числа до 10. Не всем ребятам эти знания даются легко, поэтому родителям приходится помогать чаду во время домашних занятий. Невозможно оставить без внимания этот пробел, так как знания о составе числа помогают быстро осваивать математику, ее основные азы.

Учим состав числа на домашних занятиях

Домашнее обучение позволяет облегчить школьные занятия по математике, которые в первом классе являются довольно сложными для маленьких учеников. Дети вынуждены полностью менять привычный распорядок дня и выполнять незнакомые обязанности, что отодвигает овладение знаниями на второй план. Домочадцы могут помочь маленькому ученику, если будут в ненавязчивой и увлекательной форме повторять школьные темы. Не надо браться за какие-то сложные задания, достаточно заняться основным, например, четко знать,как объяснить ребенку состав числа.

Важно! Современное образование упирается именно в освоение состава числа. Это помогает запомнить основные понятия математики. Арифметические операции и сравнение чисел будут проходить легко для ребенка.

Как учить быстрому счету

Еще до поступления ребенка в школу, родители могут быстро научить его считать до 10. Главное, сделать этот процесс максимально доступным, чтобы затем приступить к более сложным знаниям — ознакомлению детей с составом числа. Даже младшего дошкольника можно учить считать деревья, шаги, ступеньки и все окружающие предметы. При закреплении следует делать акцент на единице, правильно называть цифру «один», а не «раз», объяснить, что такое пустота, математический «0». После этого полезно показать графическое изображение цифр.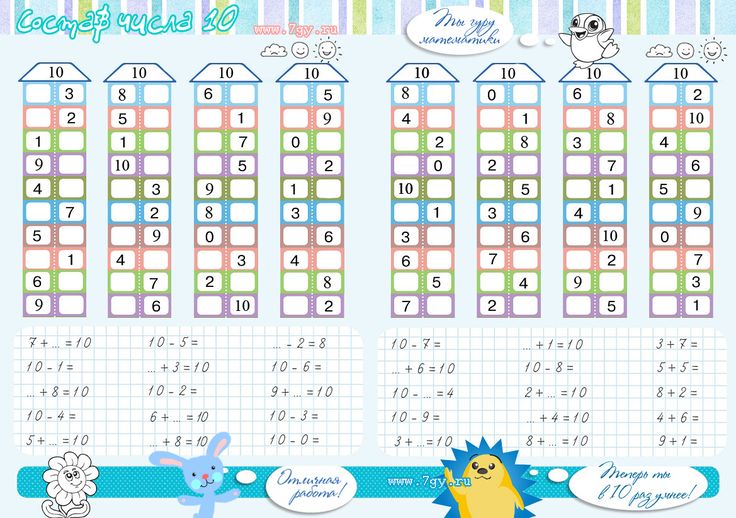

Лучше делать это в игровой форме. Следует применять наглядные примеры, пользоваться магнитными досками, цифрами, игрушками.

К сведению родителей! Нужно рассказать маленькому ученику, что цифра — это символ для записи чисел, а число — это математическое понятие. Цифр только девять, от 0 до 9, а чисел множество.

После того, как все цифры усвоены, можно приступать к счету. Следует показать, как необходимо считать на пальцах, счетных палочках, других приспособлениях. Рекомендуется сравнивать цифры, объяснять, какое число больше или меньше, насколько. Также необходимо выучить математические знаки для наглядного предоставления информации. Важно правильно объяснить, что два меньших числа могут превратиться в большее и, наоборот, большее число разделиться на два меньших.

• Чтобы запомнить состав чисел, можно поиграть с ребенком в числовые домики. Это классическое игровое упражнение. Взрослый вместе с малышом рисует несколько домиков, которые отличаются друг от друга количеством этажей. Начинать с одноэтажного, последним будет девятиэтажный. На крыше изображается определенное число. На каждом этаже по две квартиры, в которых проживают жильцы. Их количество зависит от этажности дома. Например, в трехэтажном на первом этаже живут 0 и 4, на втором — 1 и 3, на третьем — 2 и 2. Так ребенок узнает о составе числа 4.
• Можно задать число и предложить малышу назвать «соседей», какое число стоит перед ним и после него, задать два числа, спросить, что стоит между ними. Обсудить, чем отличаются числа (предыдущее — меньше на 1, последующее — больше на 1).
• На листе бумаги написать цифру и попросить найти указанное количество карандашей, горошин или стаканчиков. Поменять задание, предложить составить записанное число из разных предметов. Показать, как по-разному можно составить заданное число.
• Когда выучены цифры до 10, можно вводить понятие «единицы и десяток». Цифры могут превращаться в домики, где десятки являются этажами, а единицы квартирами. Хорошо помогают одинаковые мелкие игрушки, когда надо их выстроить по десять в два ряда. Таким образом заучивается второй десяток.

Устный счет помогает выполнять задания с максимальной скоростью. Для легкого счета нужно обязательно объяснить ребенку состав чисел, выучить в игровой форме расклад чисел до 10, причем, чем больше цифра, тем большее внимание ей уделяется. Вначале на своем примере показать, как в уме следует перебирать состав определенного числа. К примеру, нужно спросить ученика, сколько нужно еще добавить к числу 2, чтобы получить 5. Естественно, сначала возникнут сложности с усвоением, но в скором времени ребенок будет легко считать устно.

Важно! Обучая устному счету, желательно ограничить ученика в применении различных предметов, палочек и пальцев, так как это замедляет навык считать в уме.

Подходящий возраст для занятий

Оптимальный возраст для обучения счету является понятием относительным. Некоторые дети уже в 4 года пытаются считать и делают это весьма успешно, другие даже в 6 лет не готовы к этому. Однако в 5 — 6 лет следует обязательно готовить малыша к школе. Именно в этот период мозг легко воспринимает новую информацию, чадо тянется к знаниям. Воспитатели подготовительной группы основной упор делают на действия с числами в пределах 10. Дети в состоянии в этом возрасте выполнять сложение и вычитание, запомнить состав числа. Школьная программа не стоит на месте, новая тема осваивается ежедневно, поэтому без определенных навыков у ребенка могут возникнуть проблемы с математикой.

Что пригодится для домашних занятий

Сегодня для домашних занятий можно выбрать любые счетные материалы. Наиболее популярными среди них являются палочки для счета. Однако немногие задумываются над тем, что они недостаточно эффективны. Дошкольник при использовании палочек не в состоянии научиться быстро считать устно. Для ознакомления детей с составом числа предлагается использовать следующие счетные приспособления:

• Быстро выучить состав числа помогут карточки с различными предметами (домиками, цветочной полянкой, угощением для зверей), домино. Они входят в наборы для счета, как игровая форма.
  Когда малыши учатся находить составляющие чисел, к ним приходит понимание истин и основных математических понятий.
• Наборы из дерева и пластика с цифрами и математическими знаками тоже помогают ускорить учебный процесс и сделать его максимально эффективным. Различные игры с озвучиванием позволяют освоить запоминание цифр и чисел.
• Барабаны с цифрами отлично подходят для деток постарше, которые уже успели освоить математические азы. Ребенку требуется перебирать цифровые колесики, чтобы получить примеры для решения. Для малышей предусмотрены пирамидки и штыри. Перекладывание кубиков тоже способствует запоминанию чисел.
• Наиболее интересными материалами для счета станут созданные своими руками пособия. Можно вместе рисовать, клеить коробочки с цифрами, считать карандаши, лепить цифры из пластилина и теста. Все это помогает легко и прочно запомнить цифры.

Простые и доступные методики обучения

Существует множество эффективных методов, помогающих родителям понять, как научить ребенка составу числа до 10. Есть возможность выбрать для домашних занятий наиболее подходящую.

• Для облегчения подготовки к домашним занятиям можно приобрести материалы для дидактических игр, книги, обучающие предметы, мультики. Все они способствуют легкому обучению числам, составу числа, запоминанию и правильному применению. Все задания представлены в этих пособиях, родителям не надо ничего придумывать.
• Чтобы повторять школьные темы, можно воспользоваться наглядными примерами. Рекомендуется остаться с учеником в комнате вдвоем и спросить, сколько находится человек в помещении. Когда он скажет, что два, можно попросить других домочадцев по очереди входить в комнату. Пусть ребенок посчитает два плюс один и научится понимать, из чего состоит число три. Таким образом действовать дальше. Малыш должен видеть, как все происходит, почему меняются числа и как их можно складывать или вычитать.
• Для дошколят хорошо использовать игру со счетом шагов. К примеру, мама и дети отправились на прогулку. Нужно отмерять шагами расстояние и считать их по порядку. А затем возвращаться и считать шаги в обратной последовательности. Ребята быстро освоят это задание, а оно и является составом числа.
• Даже бытовые ситуации помогут выучить с ребенком состав числа. Например, попросить малыша накрыть стол к обеду, поставить 5 тарелок, столько же ложек, разложить по два куска хлеба. Если ребенок испытывает затруднения со счетом, нужно обязательно помочь ему сориентироваться, объяснить, почему нужно именно столько предметов.
• Счетные палочки помогут даже самым маленьким членам семьи научиться счету в пределах 10. Для этого следует положить на стол одну палочку, а затем попросить добавить определенное количество палочек, чтобы получилось пять. Примеры нужно постоянно усложнять, тренироваться не только увеличивать числа, но и уменьшать их.

Советы педагогов для правильного домашнего обучения

• Педагоги категорически не рекомендуют применять запись состава числа для дошкольников. Пока для них это трудно. Следует устно научить считать до 10. Желательно использовать для этого игрушки, окружающие вещи, столовые предметы, книги.
• На первом плане должны производиться действия с предметами, к примеру, был один кубик, к нему добавили еще один, стало их два, и так дальше.
• Рекомендуется как можно чаще спрашивать малыша о количестве предметов. Посчитать можно все, что находится рядом, даже ступеньки на лестнице при выходе из подъезда.

Важно! Ребенок должен четко уяснить, что каждое число меньше следующего на единицу и больше предыдущего на столько же.

Преподаватели в первом классе нередко используют классический прием для изучения цифр и чисел:

• сначала выходит один ученик и сообщает, что он первый вагон поезда;
• за ним выходит еще один и говорит, что он второй вагон;
• каждый раз проговаривается, что на один больше будет последующая цифра;
• и так дальше;
• затем вагоны называются в обратном порядке.

Основные рекомендации

1. Родители должны осознать важность изучения состава чисел, в процессе домашних занятий соблюдать некоторые рекомендации специалистов, чтобы дошкольник мог спокойно освоить информацию и правильно применить ее. Естественно, не исключены кризисы в процессе, недопонимания, но все это проходит, а остаются знания, которые необходимы при школьном обучении.
2. Нужно обязательно давать ребенку свободу. Родители часто предъявляют требования к чаду, которые не соответствуют его возможностям. Следует задуматься о запретах и наказаниях за незнание, выяснить, обоснованы ли они в действительности.
3. Необходимо учитывать мнение ребенка. Нужно понимать, что у малыша существует собственная позиция по всем вопросам. Если учить ребенка насильно, то это не принесет желаемого эффекта. Приказной тон на занятиях попросту неуместен.
4. Если малыш категорически отказывается учить цифры, то нужно поинтересоваться причинами этого. Вполне возможно, что он попросту боится расстроить родителей своим незнанием. Тогда хорошим выходом будет организация творческого процесса с привлечением всех домочадцев. Совместное изготовление пособий, рисунков из цифр, соревнования, кто быстрее назовет числа, напишет цифры, посчитает игрушки — сделает обучение легким и увлекательным.
5. Необходимо всегда позитивно оценивать достижения малыша, демонстрировать доброжелательность, показывать поддержку в сложных ситуациях, совместно устранять ошибки, обсуждать варианты возможных решений. Главное дать понять ребенку, что у него все получится, по-другому и быть не может.

Родителям важно помнить, что домашние занятия не должны вызывать неприязнь у чада. Ребятишки воспринимают подачу информации лучше всего в игре. В начале школьного учения педагоги продолжают вести занятия именно в игровой форме. Это способствует легкому и быстрому восприятию математических знаний.

Составление функций: определение, свойства, примеры

В математике композиция функции — это действие, в котором две функции, «а» и «b», объединяются для получения новой функции.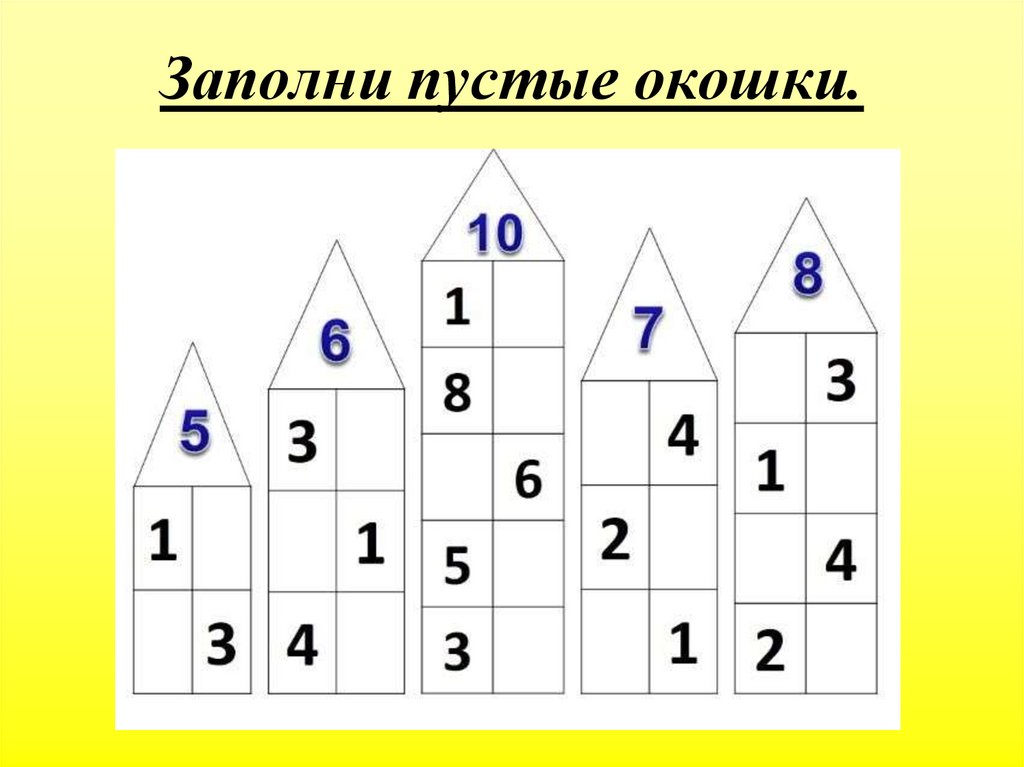 Эта новая функция ‘c’ формулируется как c(x) = b(an (x)). Это означает, что функция «b» применяется к функции x. Другими словами, когда функция применяется к выходным данным другой функции, она называется функцией составления.

Снова в школу: Прежде чем узнать о составляют функции , давайте разберемся, что такое функция. Вы можете думать о функциях как о машинах. Они принимают ввод и обрабатывают его. Выход всегда связан с входом в функцию. Функция всегда обозначается f (любая переменная или константа). Например, f(x) = x ⁴ + 21 или f(2) = 8y и т. д. Давайте посмотрим, как определяется составная функция.

Определение функции Compose

До сих пор мы учились применять значения в функции. Например, у нас есть функция f(x) = x + 7. Если мы говорим, что значение x = 2, то f(2) = 2 + 7 = 9. Просто не правда ли! Что, если мы немного поднимем планку и внутри постоянного значения поместим другую функцию внутри параметров.

Допустим, у нас есть та же функция, но вместо 2 у нас есть другая функция g(x) = 2x + 3. Поставим f (g(x)) = x + 7. Теперь значение x изменится на g(x) . Следовательно, f(g(x)) = 2x + 3 + 7 = 2x + 7.

Это основной принцип, лежащий в основе составления функций . Мы можем определить функцию композиции как приложение одной функции к другой. Возьмем две функции f(y) и g(y). Предположим, что результат f(y) отправляется через g(y). Тогда это можно записать как (g º f )(y), что указывает на то, что составляющая функция — это g(f(y)).

Аналогично, если вы хотите отправить результат g(y) через f(y), функция составления будет f(g(y)). Но помните, что g(f(y)) не равно f(g(y)). Это утверждение говорит нам, что порядок очень важен, пока мы составляем функции . Если вы не будете следовать порядку, вы можете получить другие результаты.

Представление функции Compose

Пусть две функции K и L связаны друг с другом функцией «a».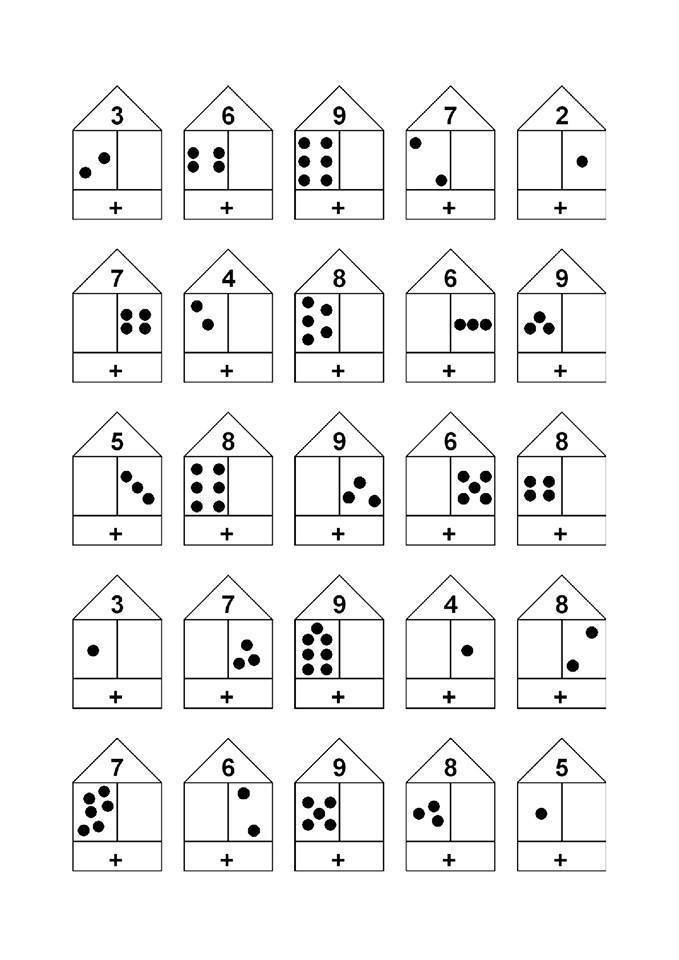 Отсюда следует, что a: K → L. Теперь предположим, что L связано с M с помощью другой функции «b». Это означает, что b: L → M. Мы видим, что K и M связаны через L. Следовательно, композиция ‘a’ и ‘b’ (a ∘ b) есть b ∘ a(x) или b(a(x )). Функция compose обеспечивает прямую связь между K и L. 

См. рисунок ниже, чтобы понять вышеупомянутые заявления:

Композиция функции является очень важной темой для классов 11, 12 и разовых партий, готовящихся к конкурсным экзаменам. Давайте изучим важные термины, связанные с функциями композиции.

Символ: Символ, используемый для определения функции составления, представляет собой маленький кружок «∘». Не поймите неправильно этот маленький кружок с точкой, используемой для умножения (скалярного произведения). Всегда пишите составляют функции как (f ∘ g)(x), а не (f.g)(x).

Домен: Домен определяется как набор всех целочисленных значений, которые входят в функцию. Числа внутри домена считаются введенными в функцию.

Как читать любые составные функции

Пусть составная функция задана как f(g(x)). Это читается как «f» из «g» из x. Мы также можем прочитать это как (f ∘ g) (x) или «туман». Здесь g(x) становится областью определения функции f.

Пример: Пусть функция f(y) равна 2x – 1, а g(y) равна 4x. Найти туман и гоф?

Решение: Дано f(y) = 2x – 1

                                  g(y) = 4x.

Следовательно, туман = ‘f’ из ‘g’ из y = f ( 4x) = 2 (4x) – 1 = 8x – 1. ) = 4 ( 2x – 1) = 8x – 4.

Этот пример также доказывает, что «туман» не равен «гоф».

Свойства составных функций

Пусть есть две функции «a», «b» и «c». Их свойства перечислены ниже→ 

1. Ассоциативность. Если есть три функции a, b и c, они называются ассоциативными тогда и только тогда, когда они удовлетворяют ассоциативному свойству композиции функций.

a ∘ (b ∘ c) = (a ∘ b) ∘ c

2. Коммутативность: свойство коммутативности утверждает, что две функции ‘a’ и ‘b’ коммутируют тогда и только тогда, когда:

a ∘ b = b ∘ a

3. Однозначная функция, производная от составной функции, всегда является взаимно однозначной.

4. Когда две функции on объединены, результатом всегда является on.

5. Обратная композиция двух функций «а» и «b» равна индивидуальной композиции обеих обратных функций.

(a ∘ b) – 1 = (a – 1 ∘ b – 1)

Составление функций

Составление двух или более функций в математике так же просто, как вишенка на торте. Однако многие ученые путают его. Посмотрите на шаги, упомянутые ниже, чтобы узнать, как создавать функции безупречно.

Шаг 1: Правильно запишите все заданные функции.

Шаг 2: Правильно прочитайте вопрос и запишите внутреннюю и внешнюю функции соответственно.

Шаг 3: Напишите внутреннюю функцию с ее фактическим значением и используйте ее для замены значения переменной.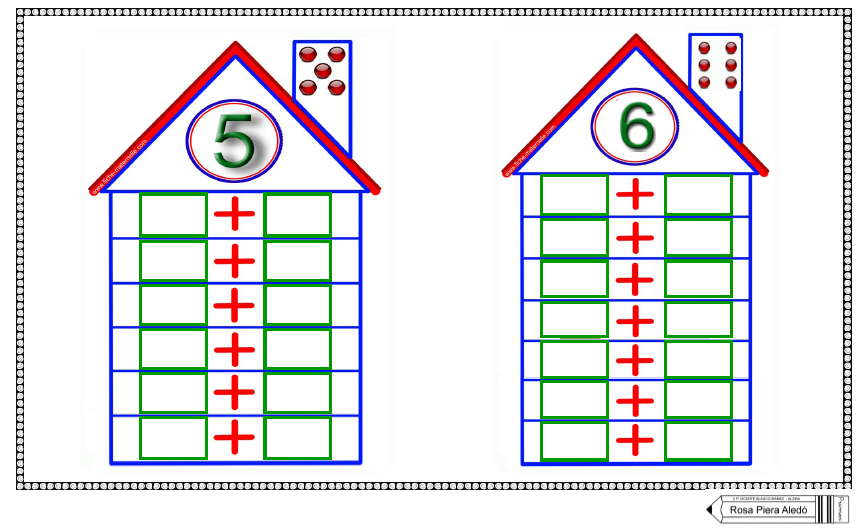

  Шаг 4: Упростите функцию, чтобы получить результирующую функцию.

Композиция функций с самой собой

Мы также можем составить функцию внутри себя. Возможно! Возьмем функцию h. Композиция h сама с собой будет следующей: 

(h ∘ h)(x) = h(h(x)), эта функция есть «h» от «h» от x.

Пример: Найдите (h ∘ h) (x) функции h(x) = 6x

Решение: Дано: h(x) = 6x

(h ∘ h)(x) = h (h (x))

= h(6x)

= 6 (6x)

= 36x

Это охватывает все темы, связанные с составлением функции. Давайте узнаем о некоторых связанных терминах и рассмотрим примеры, чтобы хорошо понять эту тему.

Домены

До сих пор это было просто, но теперь мы должны изучить домены функции. Домен — это набор всех возможных значений, существующих для функции. Функция должна работать с любым значением, которое мы ей передаем, поэтому мы обязаны убедиться, что домен точен! Например, проверьте домен на наличие √x.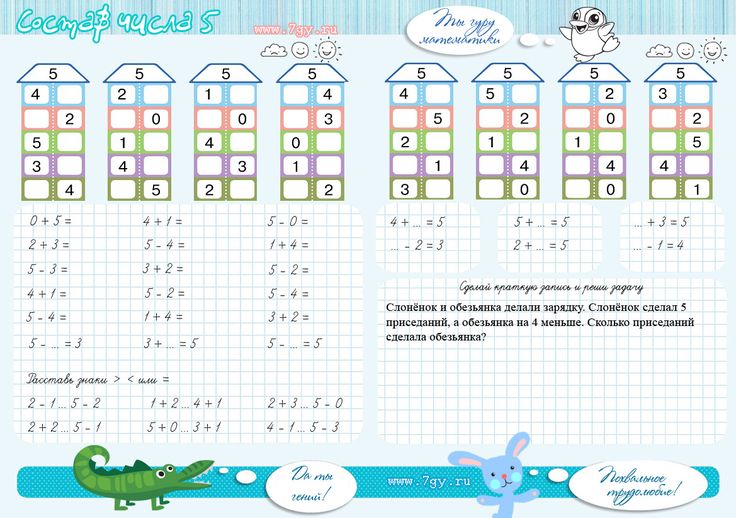

Решение: Поскольку мы знаем, что квадратный корень никогда не может быть отрицательным значением. Если да, то число мнимое. Таким образом, мы должны иметь только значения √x как положительные и действительные числа. Таким образом, область определения √x варьируется от 0 до положительной бесконечности.

Область определения сложной функции

Чтобы найти область определения сложной функции (f ∘ g) (x), мы должны сначала точно решить функцию. Область определения g(x) дает область определения составной функции. Посмотрите на пример ниже:

Пример: f(y) = √y и g(y) = y

²

Решение: Мы можем видеть, что f(y) имеет область определения, содержащую все действительные и положительные числа, а g(y) имеет все действительные числа в качестве своего домена.

Таким образом, g ∘ f (y) = g (f (y))

g(√y) = (√y) ²

         = y

-отрицательные целые числа.

Зачем нужны оба домена?

Это можно очень хорошо понять на примере.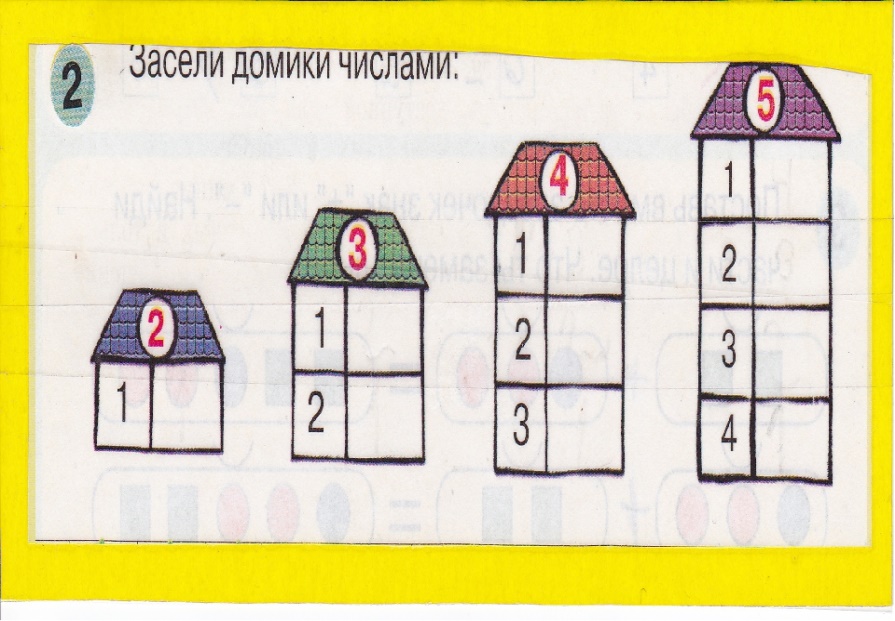 Предположим, у вас есть машина, которая использует огонь для выпекания торта, а затем покрывает его глазурью для украшения. Если мы рассмотрим их как функцию b и функцию i. Затем машина изготовит торт, используя b º i (сначала испечь, а потом украсить). Но если функции поменять местами ( i º f ), то сначала будет украшен торт, а огонь при выпечке все сожжет. Это сделает машину недостаточной.

Поэтому нам нужны оба домена.

Функция декомпозиции

Если функция слишком сложна для решения, вы всегда можете использовать метод, известный как функция декомпозиции. Это означает выполнение шагов, которые мы изучали до сих пор, в обратном порядке. Посмотрите на пример ниже:

Пример: h(y) = (y+1/y)

²

Решение: Мы можем разделить функцию следующим образом:

f(y) = y + 1/y

g(y) = y ²

Это дает нам, что

(g º f)(y) = g(y + 1/y)

= (y + 1/y) ²

Пример, связанный с составной функцией

Посмотрите на приведенный ниже пример, чтобы обобщить все концепции, связанные с составными функциями, которые мы только что изучили в предыдущей статье.

Пример:

 a(x) = x + 5 и b(x) = x ² . Найдите (а º б). Докажите также, что (a º b) ≠ (b º a).

Решение: Под «x» следует понимать входные данные функции.

Функции 

a(x) = x + 5 и b(x) = x ²

(a º b) = a (b (x))

= a (x ² )

= x ² + 5

Теперь давайте проверьте (B º A)

(B º A) = B (a (x))

= B (x + 5)

= (x + 5) ²

= x ² + 10x + 25

Мы имеем два разных следовательно, (a º b) ≠ (b º a).w

Что такое составные числа? Объяснение для начальной школы

Составные числа обратны простым числам. Здесь мы объясняем, что именно означает этот раздел теории чисел, рассказываем, как его используют и изучают в начальных школах, и приводим несколько примеров вопросов, связанных с составными числами.

Учащиеся официально знакомятся с простыми и составными числами в 5-м классе и должны работать в диапазоне от 1 до 100.

Что такое составное число?

Простое число может иметь только 2 делителя: 1 и само число. 3 будет простым числом, потому что его единственными делителями являются 1 и 3. 

Составным числом, напротив, может быть любое целое число, имеющее более двух делителей. Это может быть четное или нечетное число.

Помните, что составным числом может быть любое данное число, которое является целым положительным числом (или натуральным числом), делители которого являются меньшими целыми положительными числами, при условии, что число имеет минимум 3 делителя.

Обратите внимание, что сложное число имеет большое количество множителей, и объяснение этой концепции ученикам может помочь им вспомнить, что составное число имеет несколько множителей по сравнению с простым числом, которое имеет только два множителя.

Подробнее: Что такое факторы?

Примеры составных чисел включают:

• 4, так как оно имеет три делителя: 1,2 и 4.
• Между 10 есть 5 составных чисел: 4, 6, 8, 9, 10

1 не является ни простым, ни составным числом.

БЕСПЛАТНЫЕ рабочие листы по простым и составным числам

БЕСПЛАТНЫЙ ресурс, включающий 29 вопросов для учащихся 5 и 6 классов, чтобы помочь проверить их способность работать с простыми числами.

Составные номера в начальной школе

Термин «составные числа» официально не вводится в Великобритании до 5-го класса. множители и составные (не простые) числа, чтобы установить, является ли число до 100 простым, и вспомнить простые числа до 19».

Учащимся не будет предложено идентифицировать числа как составные вне контекста обсуждения простых чисел.

Составные числа от 1 до 100

Составные числа от 1 до 100… , 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56 , 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 , 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.

Студенты не должны заучивать этот список наизусть. Использование тестов делимости для нахождения множителей числа очень полезно при определении того, является ли число простым или составным.

Учащиеся должны знать, как находить простые числа до 100, и знать простые числа до 19. Тесты на простоту, такие как решето Эратосфена или просто пробное деление, могут быть методами, которые учащиеся используют, чтобы выяснить, какие числа являются простыми до число n, так как учащиеся будут работать в диапазоне небольших чисел.

Поэтому проще найти простые числа и знать, что числа, не являющиеся простыми, называются составными числами.

Знакомство учащихся 5-х классов с концепцией составных чисел в рамках онлайн-интервенции Third Space Learning.

Как это связано с другими областями математики?

Маловероятно, что кроме идентификации чисел как простых или составных, учащимся потребуется знать, что числа являются составными. Однако применение составных чисел используется в математике для описания формы, измерения, количественного определения количества объектов и выполнения арифметических операций.

Как это связано с реальной жизнью?

Если вы не работаете в сфере кибербезопасности (где важны простые числа) или не работаете учителем, вы вряд ли столкнетесь с термином «составные числа». Однако применение составных чисел, то есть любого целого числа, не являющегося простым, используется в математике (см. выше).

Пример работы составных чисел

В. Поместите эти числа в таблицу ниже.

2,3,4,5,6,7,8,9,10

Prime	Композит
	9039
	. 19. Они могли бы использовать это, чтобы записать простые числа в правильную часть, а затем сделать вывод, что другие числа являются составными. Prime Composite 2, 3, 5, 7 4, 6, 9, 10 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2

найдите множители каждого числа, используя их факты умножения.

2 = 2 x 1 (2 фактора)

3 = 3 x 1 (2 фактора)

4 = 4 x 1 = 2 x 2 (3 фактора)

Составные числа Примеры вопросов

1. Как определяется составное число?

(Ответ: число с более чем двумя делителями)

2. Какие из следующих чисел являются составными? 51, 97, 69, 57, 53, 90

(Ответ: 90, 69, 57, 51)

3. Энди составляет число 17 из простого числа и составного числа только сложением. Какие могут быть числа?

(Ответы: 2 + 15, 3 + 14, 5 + 12, 7 + 10, 11 + 6, 13 + 4)

4. Чему равно произведение первых 3-х составных чисел?

(ответ: 192)

5. Чен выбирает составное число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 300. Напишите все возможные составные числа, которые мог выбрать Чен.

(ответы: 25, 26, 27, 28, 30, 32, 33, 34)

Хотите знать, как объяснить своим детям другие математические слова? Ознакомьтесь с нашим словарем начальной математики или попробуйте эти:

• Что такое овладение математикой?
• Видео: как учить простые и составные числа

Вы можете найти множество рабочих листов для учеников начальных классов в Third Space Learning Math Hub.