Сочетательное и распределительное свойства умножения
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1. Вычислите удобным способом:
1) 25 * 867 * 4;
2) 329 * 75 + 329 * 246.
Решение.
1) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.
2) Имеем:
329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.
Пример 2. Упростите выражение:
1) 4a * 3b;
2) 18m − 13m.
Решение.
1) Используя переместительное и сочетательное свойства умножения, получаем:
4a * 3b = (4 * 3) * ab = 12ab.
2) Используя распределительное свойство умножения относительно вычитания, получаем:
18m − 13m = m(18 − 13) = m * 5 = 5m.
Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.
Решение.
Согласно распределительному свойству умножения относительно сложения имеем:
5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.
Такое преобразование называют раскрытием скобок.
Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.
Решение. Имеем:
125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.
Пример 5. Выполните умножение: 3 сут 18 ч * 6.
Решение. Имеем:
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
Презентация «Переместительный закон сложения» (21 слайд)
Слайд 1
Переместительный закон сложения
Кильчукова И.М.
Слайд 2
Внимательно посмотрите на выражение:
9 + 6 + 8 + 7 + 2 + 4 + 1 + 3
Слайд 3
Нам нужно найти его значение. Давайте это сделаем.
9 + 6 = 15 15 + 8 = 23 23 + 7 = 30 30 + 2 = 32 32 + 4 = 36 36 + 1 = 37 37 + 3 = 40
Слайд 4
Результат выражения 9 + 6 + 8 + 7 + 2 + 4 + 1 + 3 = 40. Скажите, удобно ли было вычислять? Вычислять было не совсем удобно. Посмотрите еще раз на числа этого выражения. Нельзя ли их поменять местами так, чтобы вычисления были более удобными?
Слайд 5
Если мы перегруппируем числа по-другому:
9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = … 9 + 1 = 10 10 + 8 = 18 18 + 2 = 20 20 + 7 = 27 27 + 3 = 30 30 + 6 = 36 36 + 4 = 40
Окончательный результат выражения 9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = 40.
Слайд 6
Мы видим, что результаты выражений получились одинаковые.
Слайд 7
Слагаемые можно менять местами, если это удобно для вычислений, и значение суммы от этого не изменится.
Слайд 8
В математике существует закон: Переместительный закон сложения. Он гласит, что от перестановки слагаемых сумма не изменяется.
Слайд 9
Дядя Федор и Шарик поспорили. Шарик находил значение выражения так, как оно записано, а дядя Федор сказал, что знает другой, более удобный способ вычисления. Видите ли вы более удобный способ вычисления?
Слайд 10
Шарик решал выражение так, как оно записано. А дядя Федор, сказал, что знает закон, который разрешает менять слагаемые местами, и поменял местами числа 25 и 3.
Слайд 11
37 + 25 + 3 = 65 37 + 25 = 62
62 + 3 = 65
37 + 3 + 25 = 65 37 + 3 = 40
40 + 25 = 65
Мы видим, что результат остался таким же, но считать стало гораздо проще.
Слайд 12
От перестановки мест слагаемых сумма не изменяется.
Слайд 13
СОЧЕТАТЕЛЬНЫЙ ЗАКОН СЛОЖЕНИЯ
Слайд 14
6 + (24 + 51) = 81 (к 6 прибавить сумму 24 и 51) Нет ли удобного способа для вычисления?
Слайд 15
Мы видим, что если прибавить 6 и 24, то мы получим круглое число. К круглому числу всегда легче что-то прибавлять. Возьмем в скобки сумму чисел 6 и 24. (6 + 24) + 51 = … (к сумме чисел 6 и 24 прибавить 51)
Вычислим значение выражения и посмотрим, изменилось ли значение выражения?
6 + 24 = 30 30 + 51 = 81
Мы видим, что значение выражения осталось прежним.
Слайд 16
Потренируемся еще на одном примере.
(27 + 19) + 1 = 47 (к сумме чисел 27 и 19 прибавить 1)
Слайд 17
Какие числа удобно сгруппировать так, чтобы получился удобный способ? Вы догадались, что это числа 19 и 1. Сумму чисел 19 и 1 возьмем в скобки. 27 + (19 + 1) = … (к 27 прибавить сумму чисел 19 и 1)
Слайд 18
Найдем значение этого выражения. Мы помним, что сначала выполняется действие в скобках.
19 + 1 = 20 27 + 20 = 47
Слайд 19
Сочетательный закон сложения: два соседних слагаемых можно заменить их суммой.
Слайд 20
Мы познакомились с переместительным и сочетательным законами сложения, а также узнали, как ими пользоваться для удобства вычисления.
Слайд 21
Мои детки 2 «В» класса МКОУ «Гимназия № 4» Вы усвоили тему ? СПАСИБО ЗА ВНИМАНИЕ!
Формула коммуникативного свойства — Что такое формула коммуникативного свойства? Примеры
Формула коммутативного свойства имеет дело с перемещением чисел. Итак, математически мы можем определить любую бинарную операцию как коммутативную, если изменение порядка операндов не меняет результат операции. Давайте узнаем о формуле коммутативного свойства с несколькими решенными примерами в конце.
Что такое формула коммутативного свойства?
Коммутативное свойство говорит о том, что порядок операндов не меняет окончательный результат. Формулы коммутативных свойств для сложения и умножения приведены ниже.
Формула коммутативного свойства
Формула коммутативного свойства для сложения: Коммутативное свойство сложения говорит о том, что изменение порядка слагаемых не изменит значения суммирования.
A + B = B + A
Формула коммутативного свойства для умножения : Коммутативное свойство умножения говорит о том, что порядок, в котором мы умножаем числа, не меняет конечный продукт.
А × В = В × А
Проверка формулы коммутативности
Попробуем обосновать, как и почему формула коммутативности верна только для операций сложения и умножения. Мы применим формулу коммутативного свойства индивидуально к четырем основным операциям.
Для сложения : Общая формула коммутативного свойства для сложения выражается как a + b = b + a. Попробуем проверить то же самое. Например, (1 + 4) = (4 + 1) = 5. Мы говорим, что сложение является коммутативным для данного набора чисел.
Для вычитания : Общая формула коммутативного свойства для вычитания выражается как (A – B) ≠ (B – A).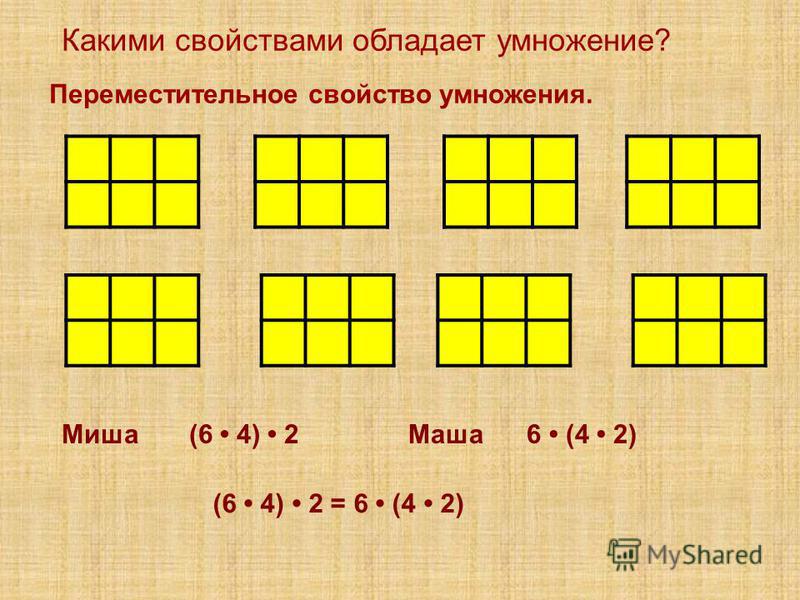
Попробуем проверить то же самое. Например, (1–4) ≠ (4–1), т. е. -3 ≠ 3. Мы говорим, что вычитание не является коммутативным для данного набора чисел.
Для умножения : для любого набора из двух чисел (A, B) коммутативность для умножения задается как A × B = B × A. Например, (2 × 4) = (4 × 2) = 8. Здесь мы находим, что умножение коммутативно для данного набора чисел.
Для подразделения : для любых двух чисел (A, B) коммутативность деления задается как A ÷ B ≠ B ÷ A. Например, (6 ÷ 3) ≠ (3 ÷ 6) = 2 ≠ 1/ 2. Вы обнаружите, что выражения с обеих сторон не равны. Таким образом, деление не является коммутативным для данных чисел.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Примеры формулы коммутативного свойства
Давайте рассмотрим несколько примеров, чтобы лучше понять формулу коммутативного свойства.
Пример 1: Если (6 × 4) = 24, то докажите, что (4 × 6) также дает 24, используя формулу коммутативности
Решение:
Поскольку умножение удовлетворяет формуле коммутативности Следовательно (6 × 4) = (4 × 6) = 24.
Пример 2: Мать Джеки спросила его, является ли x + y = y + x примером формулы коммутативного свойства. Можете ли вы помочь Джеки выяснить, является ли оно коммутативным или нет?
Решение:
Мы знаем, что формула коммутативного свойства для сложения утверждает, что изменение порядка слагаемых не изменит значение суммирования.
Итак, мы видим, что изменение порядка не изменит значение суммирования.
Следовательно, сумма остается прежней. Итак, это пример коммутативного свойства.
Ответ: x + y = y + x является примером свойства коммутативности.
Пример 3: Ринни прошла 5 миль на север, а затем 3 мили на восток.
Окажется ли она в том же месте, если бы сначала прошла 3 мили на восток, а затем 5 миль на север?
Решение:
Мы пытаемся преобразовать это в координатную плоскость. Мы предполагаем, что мили, которые он прошел на север, являются координатой y, а мили на востоке — координатой x. Используя простые правила сложения векторов, мы можем сказать, что конечное положение Ринни можно вычислить как:
Конечная позиция 1 = 5 миль на север + 3 мили на восток = (3,5)
Поэтому конечная координата = (3,5)
Теперь мы также можем сказать: конечное положение 2 = 3 мили на восток + 5 миль на север = (3,5)
.
Поэтому конечная координата = (3,5)
Ответ: Ринни окажется там же.
Часто задаваемые вопросы о формуле коммутативного свойства
Что такое формула коммутативного свойства для сложения?
Формула коммутативного свойства для сложения определяется как сумма двух или более чисел, которые остаются одинаковыми, независимо от порядка операндов.
Кроме того, формула коммутативного свойства выражается как (A + B) = (B + A)
. Что такое формула коммутативного свойства для умножения?
Формула коммутативного свойства для умножения определяется как t произведение двух или более чисел, которые остаются одинаковыми, независимо от порядка операндов. Для умножения формула коммутативного свойства выражается как (A × B) = (B × A).
Что такое формула коммутативного свойства для рациональных чисел?
Формула коммутативного свойства для рациональных чисел может быть выражена только для сложения и умножения. Общая форма задается как (P + Q) = (Q + P) или (P × Q) = (Q × P). Здесь значения P, Q представлены в виде a/b, где b ≠ 0.
Какие две операции удовлетворяют условию формулы коммутативного свойства?
Две операции, удовлетворяющие условию формулы коммутативности, – это сложение и умножение.
Объяснение коммутативных, ассоциативных и дистрибутивных свойств
Коммутативные, ассоциативные и дистрибутивные свойства или законы лежат в основе алгебры и впервые знакомятся с детьми, в очень общих чертах, в начальной школе.
В нашем руководстве для родителей мы объясняем, как ваш ребенок начнет понимать основы высшей математики.
или Зарегистрируйтесь, чтобы добавить к своим сохранённым ресурсам
Что такое коммутативное, ассоциативное и дистрибутивное свойство?
Коммутативность, ассоциативность и дистрибутивность используются в алгебре для решения задач с числами.
Свойство коммутативности, объясненное для родителей
Слово «коммутативность» происходит от «коммутировать» или «перемещаться», поэтому свойство коммутативности относится к способности перемещать числа внутри числовых предложений .
Например: 2 + 3 дает ответ 5, и если мы переставим числа так, чтобы получилось 3 + 2, мы все равно получим ответ 5. Точно так же с умножением: 6 x 4 = 24, так же как 4 x 6 = 24.
В алгебре свойство коммутативности можно записать так:
- a + b = b + a
- a × b = b × a
Свойство коммутативности применимо к сложению и умножению, но не к вычитанию или делению.
Дети младшего школьного возраста вряд ли услышат слова «переместительное свойство», но детей 2-го класса учат, что сложение чисел можно выполнять в любом порядке, а вычитание чисел нельзя .
Объяснение ассоциативного свойства для родителей
Ассоциативное свойство говорит о том, что когда мы складываем или умножаем числа, не имеет значения, как мы их группируем.
Это правило применяется к числам, сгруппированным в скобках, например: 2 + (3 + 4) или 5 х (2 х 3).
Мы заключаем расчеты в скобки, когда хотим, чтобы кто-то первым сделал эти расчеты. Однако, когда речь идет о группе чисел, которые нужно добавить, не имеет значения, куда идут скобки, ответ все равно будет тот же. Точно так же и с группой чисел, которые нужно перемножить, ответ будет одинаковым вне зависимости от того, как сгруппированы числа.
В алгебре ассоциативное свойство записывается следующим образом:
- (a + b) + c = a + (b + c)
- (a × b) × c = a × (b × c)
ассоциативное свойство относится к сложению и умножению, но не к вычитанию или делению.
Маловероятно, что дети услышат термин «ассоциативное свойство» в начальной школе, но их могут попросить решить задачу, например следующую, где применяется правило:
Три друга собрали сосновые шишки и собирают их в контейнер. Мэри и Пол собирают по 20 сосновых шишек. Джон добавляет в коллекцию еще 15. Сколько их всего?
При решении приведенной выше задачи со словами (20 + 20) + 15 = 20 + (20 + 15)
Распределительное свойство, объясненное для родителей .
Например: если мы хотим выполнить следующее умножение 2(5 +3), это означает, что мы вычисляем, сколько будет 2 лотов по 5, плюс 2 лота по 3, так что 2x можно «распределить» по 5 + 3 в 2 x 5 и 2 x 3. Это можно записать в виде следующей формулы:
- a × (b + c) = a × b + a × c
Опять же, термин «распределительное свойство» не будет использоваться в начальной школе явно, однако детей могут попросить решить аналогичную задачу на следующий:
В Березовом классе 25 детей, в Каштановом классе 28 детей.
Каждый ребенок в обоих классах должен принести пару перчаток в школу в понедельник. Сколько всего индивидуальных перчаток будет доставлено?
Здесь ребенку нужно понять, что он может решить это как:
- 25 + 28 = 53
- 2 x 53 = 106
Or they could do:
- 2 x 25 = 50
- 2 x 28 = 56
- 50 + 56 = 106
Как преподается алгебра в KS2
Дети начнут изучать алгебру в 6 классе, где они узнают, как использовать простые формулы и находить пропущенные числа в уравнениях.
В национальной учебной программе не указано, что дети KS2 должны знать об использовании скобок в расчетах. Однако возможно, что более способные дети 6-х классов познакомятся с использованием скобок; правила о порядке выполнения вычислений преподаются как BODMAS (скобки, прочее/индексы, деление, умножение, сложение и вычитание).