Переместительный закон сложения: Урок 57. законы сложения — Математика — 5 класс

Содержание

формула перемещения, сочетательное правило, решение примеров

Алгебра

12.11.21

13 мин.

Наукой, которая предшествует математике, является арифметика. Именно на ней учащиеся изучают азы вычитания и сложения. Переместительный закон является одним из основных, его нужно не только выучить теоретически, но и уметь применять на практике. Используя его сложные, громоздкие алгебраические выражения, приводят к удобному виду, что даёт возможность выполнить нужные расчёты не только безошибочно, но ещё и быстро.

Оглавление:

Общие сведения

Формулировка и применение

Сложение векторов

Примеры решения задач

Общие сведения

Арифметические действия над числами, в результате которых получается их сумма, называют сложением. В математике такую операцию принято обозначать знаком плюс (+). В общем виде формулу складывания представляют как число + число = сумма.

Числа по-другому называют слагаемыми. Ими могут быть любые числовые аргументы. Можно сказать, что при сложении происходит увеличение количества первого числа на значение аргумента второго.

Операцию возможно выполнить не всегда, а только если соблюдаются следующие условия:

Складываемые числа принадлежат единому множеству, то есть имеют одинаковый тип. Например, пусть есть одна корзина с двумя яблоками, а другая с тремя грушами и тремя яблоками. Так вот, яблоки с яблоками складывать можно, а вот с грушами — нельзя. Сложение с ними возможно, только если их объединить единым словом — фрукты.
Прибавление нельзя выполнять, если аргументы стоят под другими действиями. Например, число в квадрате нельзя складывать с другим, пока не будет выполнено действие возведения в степень.

Таким образом, после завершения операции происходит объединение чего-то в одно. Складывать можно как десятичные числа, так и цифры, записанные в любой системе исчисления.

Для десятичной, используемой в быту, характерно следующее: ноль является нейтральным числом, поэтому его прибавление не влияет на сумму. А при сложении числа с самим собой происходит удваивание.

Нужно знать, что при действии важно складывать числа начиная с меньшего разряда. При его переполнении лишние цифры переносят в следующий. Например, 126 + 37. Шесть плюс семь даст число тринадцать, согласно правилу, в единицах останется цифра три, а один добавится к десяткам. В итоге, складывая десятки, нужно будет суммировать 2 + 3 + 1. В результате будет сумма 163.

Существует два закона сложения:

Переместительный — если слагаемые поменять местами, то есть переместить относительно их знака, то результат не изменится. Математически это можно записать выражением вида: a + b = b + a.

Сочетательный — если при суммировании нескольких чисел некоторые из них заменить суммой, то ответ не изменится. То есть, a + b + c = a + k, где k = b + c.

Использование этих правил позволяет порой значительно упростить вычисления. Поэтому переместительный и сочетательный закон сложения необходимо знать. При этом подобные операции используют также при умножении и делении.

Формулировка и применение

Согласно утверждению переместительного закона, от перестановки мест слагаемых сумма остаётся неизменной. На самом деле это понятно и на интуитивном уровне. Действительно, если к двум орехам прибавить пять, то получится семь, в то же время если к пяти прибавить два, снова в ответе будет семь: 5 + 2 = 2 + 5 = 7.

Или взять другой пример с весами. Пусть на весы нужно сложить гири равные одному, трём и пяти килограммам. Не имеет значения, в какой последовательности их уложить на чашу. В итоге измерительная стрелка всё равно покажет девять килограммов. Переместительный закон можно применять к любым числам.

Из рассмотренного закона вытекает и сочетательный. Он гласит, что порядок действия со слагаемыми не имеет значения. В какой-то мере это тот же самый переместительный закон, но только расширенный. Например, нужно вычислить сумму в выражении: 1 + 6 + 19 + 34 + 10. Конечно же, совсем несложно сложить члены и последовательно, как они расставлены в задании, но легче будет всё же их сгруппировать следующим образом: (1 + 19) + (34 + 6) + 10 = 20 + 40 + 10 = 70. Результат будет тот же, что и при последовательном складывании, а вот сами вычисления проще.

Сочетательный и закон перемещения нашли своё применение не только в арифметике, но ещё и в умножении. Опираясь на них, был сформулирован переместительный закон сложения и умножения. Он гласит, что для того, чтобы найти произведение числа и суммы, необходимо каждое из слагаемых умножить на множитель, а затем полученные результаты сложить. То есть при решении нет необходимости выполнять сначала действие в скобке, а после искать произведение. Например, (15 + 42) * 2 = 15 * 2 + 42 * 2 = 30 + 84 = 114.

Этими законами прежде всего необходимо научиться пользоваться на практике. Конечно же, поставленные задания на расчёты можно решать и не прибегая к упрощениям. Но часто такие вычисления не только занимают много времени, но и повышают вероятность возникновения ошибки.

Поэтому перед тем как переходить непосредственно к расчётам, нужно упрощать задание. Например, 224 + 295 + 2 * (156 + 312) + 305 = 224 + 295 + (2*156 + 2 * 312) + 305 = 224 + 295 + 780 + 305 = (224 + 780) + (295 + 305) = 1004 + 600 = 1604. На самом деле при определённом опыте, пользуясь упрощением, даже в уме можно решать примеры, довольно сложные на первый взгляд.

Сложение векторов

Вектором называют любую прямую линию, у которой есть начало и конец. Фактически же это отрезок, имеющий направление. Обозначают его двумя большими буквами, символизирующими начало и конец, или маленькой латинской. Обязательно над символом ставится знак чёрточки или стрелочки.

Вектор используется не только в математике, но и для обозначения различных сил в физике. Если отрезок рассматривается в системе координат, то он задаётся набором своих данных. Поэтому часто любую упорядоченность чисел тоже называют вектором. Это название особенно актуально для информатики. С векторами возможны различные математические действия. Например, их можно складывать и вычитать. По отношению к ним можно также использовать переместительный и сочетательный (ассоциативный) законы.

От произвольной точки на плоскости A можно отложить прямую, ограниченную точкой B. Из первой точки также можно построить другой, непараллельный первой линии отрезок, заканчивающийся точкой D. При этом вектора AB и AD будут равны. Параллельно нарисованным линиям можно провести такие же, то есть построить параллелограмм ABCD. Опираясь на правило треугольника, верно утверждать, что сторона AC равна сумме векторов AB + AD. Аналогично отрезок AC можно найти, сложив вектор AD и DC. Отсюда следует, что сумма AB + AD = AD + DC. Другими словами, a + b = b + a. Что и следовало доказать.

Пусть имеется вектор AB = a. Из точки B можно построить вектор BC, равный b, а от точки C ограниченную прямую CD, равную c. Затем возможно соединить точку D и С, B и D, A и C. Применив правило треугольников, можно записать следующее равенство: (a + b) + c = (AB + BC) + CD = AC + CD = AD.

Верной будет и такая запись: a + (b + c) = AB + (BC + CD) = AB + BD = AD. Следовательно, от перестановки векторов результат не изменяется.

При доказательстве сочетательного закона использовалось так называемое правило параллелограмма, используемое при сложении неколлинеарных векторов. Формулируется оно следующим образом: чтобы сложить векторы a и b, нужно от общей точки отложить два вектора и построить параллелограмм. Тогда вектор, определяющийся диагональю фигуры, равен сумме векторов, совпадающих со сторонами параллелограмма.

Примеры решения задач

Важно не просто понимать законы арифметики, но и уметь их использовать на практике. Для этого необходимо получить опыт самостоятельных решений. Существуют сборники задач, по которым можно прорешать предлагающиеся примеры.

Вот некоторые из них, рассчитанные на учеников младших классов:

Вычислить выражение в уме: 43 + 28 + 52 + 37 + 2. В силу того, что человеку из-за особенностей мышления проще складывать десятки, чем, например, суммы чисел 7 + 8, 5 + 7, 8 + 3, 5 + 8, то, используя сочетательный закон числа, можно распределить в другом порядке. То есть 43 сложить с 37 и получить в ответе 80, затем к 28 прибавить 52, что даст тоже 80. Теперь останется сложить две цифры 80 и к ним добавить двойку. В ответе получится 162.
Вычислить ответ, используя правило сложения: (-1 + 3) + (-18) = -1 + (3 + (-8)) = -1 + (-5) = -6.
Не всегда попадаются задачи с целыми числами. К дробным также можно применить распределительный закон. В первую очередь нужно складывать отношения с одинаковыми знаменателями и группировать дроби так, чтобы получалось целое число.1/ 9 + ¾ + ¼ + ½ + 7/9 + ½ = (1/9 + 7/9) + (¾ + ¼) + (½ + ½) = 8/9 + 4/4 + 1 = 8/9 + 2 = 2 8/9.

Найти сумму трёх векторов со следующими координатами: a (17; 2), b (12,4), c (3; -61). Для того чтобы найти сумму, по правилу необходимо сложить соответствующие координаты. То есть необходимо выполнить следующее действие (17 + 12 + 3, 2+ 4 + (-61)). Конечно же, в первом члене проще 17 сложить с тройкой, а после добавить 12. Во второй же координате последовательность можно оставить без изменения. В итоге получится, что сумма векторов равняется (32, -55).

Придумать такие задачи можно и самостоятельно. Для дальнейшего успешного применения правил в реальных заданиях обычно достаточно самостоятельно решить около 20 примеров.

Рассмотренные базисные приёмы очень важно понять для дальнейшего успешного изучения математики.

Переместительный и сочетательный законы сложения помогают довольно сильно облегчить ту или иную задачу. Используя правила, можно из громоздкой и неудобной к восприятию записи получить простое выражение, которое, возможно, можно будет посчитать даже в уме.

Переместительный закон сложения — правило и примеры решения задач » Kupuk.net

В математике для решения задач применяются сочетательный и переместительные законы сложения. У многих учеников они могут вызвать некоторые сложности, поскольку не все понимают школьную программу 5 класса. Для этих целей специалисты разработали универсальный алгоритм обучения, который позволит не только хорошо усвоить материал, но и претендовать на высокие оценки.

Общие сведения

Сложение — математическая операция, при помощи которой происходит увеличение исходного числа на определенное значение. Ее элементами являются минимум два слагаемых и результат. Последний называется суммой. Всего существуют два закона сложения. К ним относятся следующие:

Коммутативный.

Ассоциативный.

Первый еще называется переместительным, а второй — сочетательным. Многие школьники путают правила сложения и умножения. Следует отметить, что для последнего предусмотрены три закона, т. е. распределительный, сочетательный и переместительный. У деления и умножения правила похожи, а вот для вычитания, как и для сложения, предусмотрено также два свойства.

Чтобы не путать термины, необходимо рассмотреть каждое арифметическое действие по группам.

Сложение и вычитание

Сложение и вычитание являются взаимосвязанными математическими операциями. Для примера необходимо разобрать числовое выражение «10+20+30+40=100». Оно состоит из пяти элементов: четырех слагаемых и одного результата. Это математическое выражение можно записать в обратном виде 100−40−30−20=10. Данное тождество называется вычитанием.

Иными словами, вычитание — математическая операция уменьшения заданного числа (уменьшаемого) на определенное число (вычитаемое), результатом которой является разность. Для сложения и вычитания применимо всего два закона: переместительный и сочетательный. Они используются для оптимизации вычислений.

Следует отметить, что методика ускорения расчетов используется также в программировании и информатике. Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.

Переместительное правило

Переместительный закон сложения гласит: от перемены мест слагаемых значение суммы не изменится. Для доказательства этого утверждения можно воспользоваться числовым выражением 12+32+16+40=100.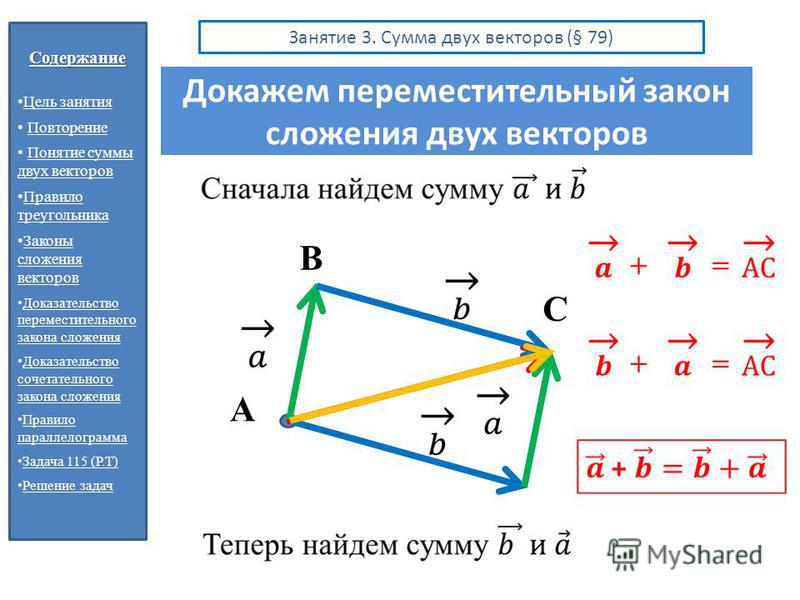 Если поменять местами элементы (слагаемые) в левой части, то должна также получиться сотня, т. е. 32+12+40+16=100. Утверждение доказано. Математическая запись или формула закона выглядит таким образом: R+T+S=T+S+R=S+T+R=M.

Специалисты рекомендуют самостоятельно придумать числовое выражение и доказать истину формулировки переместительного свойства. Для вычитания также существует переместительный закон, который может быть сформулирован следующим образом: если поменять местами вычитаемое, то разность останется прежней.

Для доказательства правила можно использовать такой же видоизмененный пример, что и для суммы «100−40−16−32=12». В нем вычитаемое эквивалентно группе элементов 40, 16 и 32. Если эти числа поменять местами, то результат не изменится, т. е. 100−32−40−16=12. Правило доказано. Для вычитания переместительный закон записывается в таком виде: М-R-T=S, М-R-S=T и М-T-S=R. Далее необходимо рассмотреть сочетательные правила.

Сочетательный закон

Сочетательное правило сложения и вычитания похожи. Их суть заключается в перегруппировке элементов. Следует отметить, что последняя не влияет на результат. Она необходима для упрощения вычислений. Сочетательный закон сложения формулируется таким образом: значение суммы не зависит от группировок слагаемых.

Например, 4+11+6+9=30. Для удобства можно записать пример в таком виде: (4+6)+(11+9)=30. Результат не изменился. Кроме того, производить вычисления стало проще. В виде формулы закон можно записать в таком виде: М+R+T=М+(R+T)=(М+T)+R=S.

Для вычитания формулировка правила звучит следующим образом: разность не изменится, если перегруппировать вычитаемые компоненты, т. е. 30−6−11−4=30-(6+4)-4=9. Формула закона имеет вид: М-R-T-P= М-R-(T+P)= N. Следует отметить, что числа можно группировать в произвольном порядке. Главное — придерживаться принципа вынесения знака за скобку (касается только вычитания).

Некоторые ученики часто приписывают к арифметическим операциям сложения и вычитания распределительное свойство. Это большая ошибка, поскольку для суммы и разности его не существует вообще. Далее необходимо рассмотреть операции, в которых оно применяется.

Произведение и деление

Для умножения и деления применимы те же правила, что и для сложения и вычитания, но к ним добавляется еще и третье — распределительное свойство. В итоге список законов имеет такой вид:

Переместительный.

Сочетательный.

Распределительный.

Следует отметить, что формулировки для переместительного закона сложения и умножения практически идентичны. Для последней математической операции он звучит таким образом: произведение не изменится, когда будет выполнено перемещения одного сомножителя на место другого. Например, 2*3*4=2*4*3=24.

В математической форме правило записывается в виде соотношения «RST=SRT=TRS=O». Для деления также используется возможность перемещения делителей, т. е. O: S: T=R или O: Т: S=R. На примере реализация правила выглядит таким образом: 60:2:15=2 или 60:15:2=2.

Для умножения сочетательный закон формулируется в таком виде: значение произведения не изменится при группировке в любом порядке сомножителей, т. е. S*T*R=S*R*T=R*T*S=N. Для деления у него немного другой вид: делители могут группироваться в любом порядке, и это не повлияет на частное. Математическая форма записи выглядит следующим образом: N: T: R: M=N:T:(R:M)=O.

Распределительное свойство для умножения и деления формулируется практически одинаково: произведение (деление) суммы или разности двух элементов на число эквивалентно умножению (делению) каждого элемента суммы или разности на искомый элемент. Законы имеют такие формы записи:

Умножение: (S+T)*M=SM+TM или (S-T)*M=SM-TM.

Деления: (S+T)/M=S/M+T/M или (S-T)/M=S/M-T/M.

Если обратить внимание на формулы, то для сложения запись невозможна, поскольку это уже будет сочетательный закон. Например, в первом пункте необходимо заменить знак «*» на сложение. Соотношение будет иметь следующий вид: (S+T)+M — сочетательное свойство операции сложения. Далее необходимо разобрать пример на применение всех законов.

Пример задачи

Для закрепления теоретического материала специалисты рекомендуют разобрать пример, в котором можно будет применить все законы арифметических операций. Числовое выражение задачи имеет такой вид: 5+6+5+4+20+(25+100)/5+(11+4)*4. Необходимо вычислить результат оптимальным методом. Решать задание нужно по такому алгоритму:

Переместительный: 5+5+4+6+20+(25+100)/5+(11+4)*4.

Сочетательный: (5+5+20)+(4+6)+(25+100)/5+(11+4)*4.

Распределительный: (5+5+20)+(4+6)+25/5+100/5+11*4+4*4.

Математические преобразования: 40+5+20+44+16

Переместительный: 40+20+44+16+5.

Сочетательный: (40+20)+(44+16)+5.

Вычисление и результат: 125.

Следует отметить, что к числовому выражению свойства арифметических операций можно применять многократно. Специалисты рекомендуют использовать алгоритм такого вида для оптимизации вычислений.

Таким образом, законы математических операций применяются для оптимизации вычислений для нахождения результатов.

Основные законы сложения и умножения

Основные законы сложения и умножения — МАТВОКС

Перейти к содержанию

ПОИСК

Страница Вконтакте открывается в новом окне

Вы здесь:

Основные законы сложения и умножения

Переместительный закон сложения.
Сочетательный закон сложения.
Переместительный закон умножения.
Сочетательный закон умножения.
Распределительный закон умножения по отношению к сложению.

1. Переместительный закон сложения.

От перестановки мест слагаемых сумма не меняется:

Пример:

Действительно:

2 Сочетательный закон сложения.

Результат сложения нескольких слагаемых не зависит от порядка действий.

Или можно сочетательный закон сложения сформулировать иначе.

Сумма нескольких слагаемых не изменится, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой.

Этот закон позволяет группировать слагаемые для удобства их вычислений.

Пример

Действительно,

Этот

пример отчетливо показывает важность сочетательного закона сложения.

Пусть нужно найти значение выражения:

Если не пользоваться сочетательным законом, то, будем складывать числа последовательно:

1 действие

2 действие

Тогда:

А теперь

воспользуемся сочетательным законом сложения.

Если внимательно посмотреть на выражение, то, очевидно, проще сначала сложить 5 и 95, а затем прибавить 37.

1 действие

2 действие

Тогда:

Очевидно, второй способ вычисления выражения удобнее использовать.

3. Переместительный закон умножения

От перемены порядка сомножителей произведение не изменится.

Пример:

Действительно:

4. Сочетательный закон умножения

Результат произведения нескольких множителей не зависит от порядка действий.

Или можно сочетательный закон умножения сформулировать иначе.

Произведение нескольких сомножителей не изменится, если какую-нибудь группу рядом стоящих сомножителей заменить их произведением.

Этот закон позволяет группировать множители для удобства их вычислений.

Пример

Действительно,

Этот пример отчетливо показывает

важность сочетательного закона умножения.

Пусть нужно найти значение выражения:

Если не пользоваться сочетательным законом, то, будем перемножать числа последовательно:

1 действие

2 действие

Тогда:

А теперь

воспользуемся сочетательным законом умножения.

Если внимательно посмотреть на выражение, то, очевидно, проще сначала перемножить 0,5 и 10, а затем результат умножить на 13.

1 действие

2 действие

Тогда:

Очевидно, второй способ вычисления выражения удобнее использовать.

5. Распределительный закон умножения по отношению к сложению

Распределительный закон умножения позволяет вместо умножения суммы на число, умножить каждое слагаемое по отдельности на число, после чего результат сложить.

Чтобы умножить сумму двух (или нескольких) чисел на какое-либо число, можно каждое слагаемое умножить на это число и полученный результат сложить.

или:

Распределительное свойство справедливо и в том случае, когда число умножается на сумму трех и более слагаемых, например,

Пример 1

Пример 2

Число 2 является общим множителем.

или:

Иногда бывает выгоднее поступить наоборот. Вместо того, чтобы умножать каждое слагаемое на одно и то же число, сначала находят сумму этих слагаемых и умножают ее на данное число. Это действие называют «внесение множителя в скобки»:

Пример 1

Пример 2

Если при умножении суммы на число

множитель вносят в скобки, умножая каждое слагаемое на этот множитель (скобки затем опускают):

то при

вынесении множителя за скобки, каждое слагаемое делят на этот множитель:

Из переместительного и сочетательного свойств сложения следует

следующее свойство:

В любой

сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.

Пример

Найти значение выражения:

Решение

Очевидно, что проще сложить 1,18 и 4,32, а также 12,1 и 1,4. Так как от перестановки мест слагаемых и от порядка действий сумма не меняется, то можем записать:

Из свойств произведения следует

следующее свойство:

В любом

произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.

Пример

Вычислить:

Очевидно, что проще перемножить 0,5 и 28, а также 0,25 и 4. Так как от перестановки мест множителей и от порядка действий произведение не меняется, то можем записать:

9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3

MATHVOX

Вверх

Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять

Privacy & Cookies Policy

Don`t copy text!

Сочетательный закон сложения — формулировка, правило и примеры

Арифметические операции изучаются на уроках математики во втором классе. Одной из них является сложение, сочетательный закон которого позволяет значительно повысить скорость решения различных заданий. Однако не все ученики могут разобраться и досконально изучить материал. Специалисты предлагают собственную методику успешного обучения и повышения успеваемости.

Содержание

Общие сведения
- Переместительное правило
- Сочетательный закон
- Методика применения
Пример решения

Общие сведения

Сложение является одной из базовых арифметических операций в математике. Оно изучается во втором классе общеобразовательной школы. Существует всего 2 правила: переместительный и сочетательный закон сложения. Однако многие ученики часто их путают. Разобраться в этом помогут специалисты. Они разработали специальную методику, позволяющую быстро запомнить различие между ними.

Однако для изучения алгоритма нужно знать базовые термины и определения. К ним относятся:

Сложение — операция, направленная на увеличение числового значения на заданную величину.

Законы — набор правил, позволяющих оптимизировать расчетные процессы, т. е. проще посчитать какое-либо значение.

Сложение состоит минимум из трех элементов: двух слагаемых (одно из них увеличивается на другое) и результата. Последний называется суммой. На примере это выглядит так: 5+9=14, где 5 — I слагаемое, 9 — второй элемент-слагаемое или число, на которое нужно увеличить первое слагаемое, а 14 — их сумма.

Переместительное правило

Переместительное (коммутативное) правило является очень простым для понимания. Оно формулируется следующим образом: если поменять местами слагаемые, их сумма не изменится. Математическая форма записи закона выглядит следующим образом: q+w=s.

На практическом примере правило реализуется в таком виде: 5+6=6+5=11. Последнее числовое выражение очень легко проверить. Для этого достаточно воспользоваться обыкновенным калькулятором. При сложении 5 и 6 он покажет величину, равную 11. Следует отметить, что таким образом и доказывается закон переместительного свойства сложения.

Прием практической реализации для доказательства правил и утверждений применяется очень часто. Это и есть оптимальная методика, позволяющая выяснить работоспособность того или иного утверждения. Далее необходимо рассмотреть сочетательный закон сложения.

Сочетательный закон

Сочетательное правило сложения возможно применить, когда числовое выражение включает в свой состав от трех и более слагаемых. Сочетательный закон сложения во 2 классе можно сформулировать следующим образом: слагаемые, входящие в состав выражения, можно для удобства складывать в любом порядке.

Очень часто правило называют ассоциативным свойством операции сложения. Ее математическая запись имеет такой вид: p+r+s=(p+s)+r=(s+r)+p=z. Чтобы доказать утверждение, нужно решить пример «2+9+8+1». Его специалисты рекомендуют решать по такому алгоритму:

Разбить на пары слагаемые: (2+8)+(9+1). Необходимо руководствоваться удобством вычислений, поскольку пару чисел «2+8» легче сложить, чем «2+9».

Выполнить вычисления в скобках (символах группировки) и записать результат: 10+10=20.

К сочетательному свойству также можно применить и переместительное (коммуникативное) правило. Этим приемом очень часто пользуются специалисты. Кроме того, по-другому ассоциативный закон называется методом группировки чисел. Далее нужно рассмотреть методику применения двух законов на практике.

Методика применения

Методика использования правил сложения зависит от конкретного примера. Однако специалисты рекомендуют придерживаться следующего алгоритма нахождения результатов числовых выражений:

Проанализировать пример и найти в нем числа, сложение которых можно произвести очень быстро.

Сгруппировать элементы при помощи круглых скобок (ассоциативный закон) или просто поменять их местами (переместительное свойство).

Вычислить значения сумм пар, находящихся в скобках.

Записать результат.

Сочетание элементов можно выполнять несколько раз, т. е. вычислить сначала одно значение, а потом опять перегруппировать выражение. Перемену мест слагаемых можно производить в несколько заходов.

Кроме того, законы сложения можно применять не только для целых чисел, но и для дробных. Для совершенствования качества усвоения теоретического материала рекомендуется придумать примеры и решить их.

Некоторые ученики часто путают принадлежность распределительного правила к суммации двух и более величин. Этого делать не нужно, а требуется запомнить, что у сложения только 2 закона, но не 3. Последний принадлежит только операциям деления и умножения.

Переместительное и сочетательное свойства можно применять и для вычитания. Далее необходимо на практическом примере разобрать использование правил сложения и методику их применения.

Пример решения

Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:

Пишется пример: 4+9+6+5+1+15+17+2+12+1.

Переместительное свойство: 4+6+9+1+5+15+17+2+12+1.

Сочетательный закон: (4+6)+(9+1)+(5+15)+(17+2+1)+12.

Вычисление значений: 10+10+20+20+12=60+12=72.

Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.

Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.

Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.

МатематикаСчётные и несчётные множества — понятие, свойства и примеры

МатематикаИррациональность дроби — как правильно избавиться от знака корня в знаменателе?

Конспект урока для 1 класса «Переместительный закон сложения»

Конспект урока для 1 класса

«Переместительный закон сложения»

Учитель начальных классов: Дёмина Татьяна Ивановна, МОБУ СОШ №21,

г. Белорецк, Республика Башкортостан.

Тип урока: изучение нового.

Вид урока: урок-сказка

Цель урока: познакомить с переместительным свойством сложения.

Задачи урока:

Образовательные: формировать умения сравнивать числа и их упорядочивать, применять переместительное свойство сложения, учить устанавливать закономерности.

Развивающие: развивать навыки устного счёта, способствовать развитию логического мышления, математической речи обучающихся.

Воспитательные: воспитывать навыки контроля и самоконтроля, аккуратность, положительную мотивацию к изучаемому предмету.

Оборудование: мультимедийная презентация.

Ход урока

Организационный момент

Начинается урок,

Он пойдет ребятам впрок.

-Постараюсь все понять.

Многое хочу узнать! (Слайд 2)

А урок математики у нас сегодня не простой, мы отправимся сегодня в гости, в гости к гномам. Гномы очень трудолюбивые, многое знают и умеют, но сегодня им понадобится ваша помощь, и мы сегодня вместе с гномами постараемся вывести новое правило сложения.

Ну что ж!

Где играют дружно,
Считают умело,
Там и сказке можно
Появиться смело.

Жили-были гномики в уютном своем домике

На лесной опушке у маленькой речушки.

Братцев этих ровно семь,

Вам они известны все.

Каждую неделю кругом,

Ходят братцы друг за другом.

— Догадались, как зовут гномов? (Слайд 3) Послушайте песню и скажите, как зовут гномов.

— Имена гномов — это названия дней недели.

— Назовите по порядку все дни недели.

Гномики предлагают вам в течении урока подумать и разгадать ребусы, а в конце урока мы к ним вернемся и проверим, кто смог разгадать. (Вывешивается на доску карточка: а+а=а к+а=к)

Устный счет

ПОНЕДЕЛЬНИК – не бездельник,

Любознательным он рос.

И для вас, ребята,

Приготовил БЛИЦ-ОПРОС! (Слайд 4)

-Назовите число, следующее за числом 6, 4, 9.

-Назовите число, предшествующее числу 5, 8, 2.

-Назовите числа, которые меньше 3.

-Назовите числа, которые больше 8.

-Какое число не является натуральным?

-Назовите натуральный ряд чисел.

-Какое число стоит между числами 5 и 7, 2 и 4, 8 и 10?

-Сравните числа 1 и 4, 7 и 5, 0 и 2, 5 и 5.

-Прочитать выражение по-разному: 5 + 1 = 6, 8 – 1 = 7 (Карточка на доске)

-Расположите числа в порядке возрастания, убывания. (Карточка на доске)

Молодцы! С заданием справились отлично.

ВТОРНИК неделю продолжает,

Всех трудиться заставляет.

Любит солнце и цветы,

Поработай с ним и ты. (Слайд 5)

ВТОРНИК очень любит выращивать цветы. И вот однажды у него вырос необычный цветок, на лепестках которого были примеры, давайте поможем

ВТОРНИКУ решить их. (Устное решение примеров.)

Чтобы у вас было хорошее зрение, ВТОРНИК приготовил для вас физпаузу для глаз. Следите глазками за цветами.

ФИМИНУТКА для глаз.(Слайды 6 – 19)

Подготовка к изучению нового.

СРЕДА — кладоискатель.

Золото из земли добывает,

А как пересчитать – не знает! (Слайд 20) (На доске 3 ученика. )

Сравните две суммы каждого столбика. Найдите значения сумм по таблице сложения.

Но мы хотим гномику сказать, что «Золото добывают из земли, а знания из книги». Кто много читает, тот многое узнает, а знания ценятся так же дорого, как и золото. И книги нам сегодня помогут вывести новое правило.

Изучение нового.

(Слайды 21 -26)

-Сколько изображено книг в синих обложках? (2 книги). Положите на парту слева столько же треугольников.

-Сколько книг в красных обложках? (3 книги). Придвиньте к треугольникам столько же квадратов.

-Сколько всего книг? (5). Сколько у вас фигур на партах? (5).

-Как получили число 5? (к 2 прибавили 3).

-Как запишем сумму? (2+3=5). /Сверяем свои записи с записями на слайде/

-Как называется число 2 при сложении? (первое слагаемое).

-Как называется число 3 при сложении? (второе слагаемое).

-Как называется число 5? (значение суммы).

-А теперь посмотрите на экран: что произошло? (синие и красные книги поменялись местами).

-Какие книги теперь стоят на первом месте? (Красные). Сколько их? (3).

-Какие книги на втором месте? (Синие). Сколько их? (2).

-Сколько всего книг? (5).

-Поменяйте местами свои фигурки на партах.

-Сколько теперь треугольников и сколько квадратов? (3 квадрата и 2 треугольника).

-Сколько всего фигур? (5).

-Составьте сумму (3+2=5). /Сверяем свои записи с записями на слайде/

-Как теперь называются числа? (3 – первое слагаемое, 2 – второе слагаемое, 5 – значение суммы).

-Что произошло со слагаемыми? ( Они поменялись местами)

-Изменилось ли значение суммы после перестановки слагаемых? (Нет)

-Какой можем сделать вывод? (От перестановки слагаемых сумма не изменилась)

(Слайд 27)

Прочитайте правило в учебнике на стр. 32.

Закрепление изученного.

ЧЕТВЕРГ очень любит птичек,

И голубок, и синичек.

Кормит птичек он всегда,

Помогает в холода.

А кто из вас помогает зимой птичкам? Как мы можем помочь?

Помогите гномику накормить птичек. Составьте выражение и найдите значение выражения. Примените переместительное свойство сложения.(Слайд 29) (Письмо с комментированием.)

ФИЗМИНУТКА (Слайд 28)

Гномы вышли по порядку –

Раз-два-три-четыре!
Дружно делают зарядку —
Раз-два-три-четыре!
Руки выше, ноги шире!
Влево, вправо, поворот,
Наклон назад,
Наклон вперёд. (Под музыку ученики выполняют физические упражнения.)

А сейчас наше тело отдохнуло, пусть поработает ум.

Решение логической задачи

ПЯТНИЦА следует за братом,
У него идей богато,
Он за все берется смело,
И работа закипела. (Слайд 30)

Однажды ПЯТНИЦА распиливал бревно, и он задумался, а сколько ему нужно сделать распилов, чтобы получить 4 части этого бревна? (Устное решение логической задачи.)

Работа в тетради . С.21, № 41 (Слайд 30) Посоветуйтесь друг с другом и найдите правильное решение. Что нужно сделать, чтобы найти самое длинное и самое короткое бревно? Практическая работа: вырезают и наклеивают.(Работа в парах.)

А сейчас снова вернемся к теме нашего урока. Какое правило мы сегодня изучили?

Самостоятельная работа.

А СУББОТА предлагает вам работу.

Делать все должны старательно,

Для Вас работа самостоятельная.

Учебник с. 32, № 69. (Слайд 31) (Самостоятельная работа) Проверка.

Работа с геометрическим материалом.

В гости ходит ВОСКРЕСЕНЬЕ,
Очень любит построенье.
Это самый младший брат,
К Вам зайти он будет рад.

Давайте построим дом, куда бы мы могли пригласить гнома.

Итог урока

Так и жили гномики

В чистом своём домике

На лесной опушке

На радость всем зверюшкам!

Сегодня на уроке мы с вами были в гостях у весёлых, трудолюбивых гномов. Мы узнали переместительное свойство сложения.

Как звучит это правило?

Все сегодня работали со старанием, показали своё трудолюбие. Я говорю вам всем сегодня:

Молодцы!

Спасибо за урок! На память о нашем уроке для вас наградки.

А какое у вас настроение после нашего урока вы покажете, прикрепив на нашу поляну показатель своего настроения.

Урок математики (2 класс) «Законы сложения»

Тема урока: Переместительный и сочетательный законы сложения.

Тип урока: урок изучения нового материала.

Цель урока: ознакомить учащихся с законами сложения.

Задачи урока:

1. Ознакомить учащихся с переместительным и сочетательным законами сложения

2.Учить применять законы сложения для рационализации вычислений

3.Продолжить работу над решением задач на нахождение периметра прямоугольника

4.Развивать вычислительные навыки, логическое мышление, интерес к математике как к учебному предмету

5.Воспитывать чувство товарищества, умение доводить начатое до конца

Оборудование: проектор, компьютер, мультимедийное приложение к учебнику «Математика», презентация к уроку.

Ход урока:

1.Организационный момент

Проверили готовность к уроку.

2.Проверка домашнего задания

-Что было задано?

-Нужно было составить задачу по краткой записи и решить ее, также найти значение выражений.

-Каким действием решили задачу? Почему?

-Решили задачу сложением, потому что было больше, чем продали и осталось.

-Прочитайте решение, ответ. Проверим выражения.

-У кого нет ошибок при выполнении домашнего задания?

-Отступаем от домашней работы 4 клеточки и записываем число, классная работа.

По-прежнему не всем удается красиво писать цифру 8. Потренируемся в написании этой цифры.

Обведите карандашом самую красивую 8. Кто считает, что цифры получились очень хорошо?

Физминутка

3.Сообщение темы и постановка цели урока

Для того, чтобы узнать тему нашего урока мы должны расшифровать ее. Вы будете работать в группах по 4 человека. Вы получаете шифровку, расшифровав которую вы получите толь часть задания. И только когда все шифры будут расшифрованы, сложив их вместе, вы сможете узнать нашу тему.

1 группа:

12-7=

9+8=

11-3=

ЗАК

2 группа

5+6=

11-4=

16-7=

ОНЫ

3 группа

18-8=

15-9=

13-2=

СЛО

4 группа

84-80=

37-7=

14-4=

ЖЕН

5 группа

42-40=

59-9=

9+6=

ИЯ.

6 группа

25-20=

9-6=

11-2=

6-5=

6+8=

10+9=

8-4=

З А К О Н Ы С Л О Ж Е Н И Я .

И З У Ч А Е М

5 17 8 11 7 9 10 6 11 4 30 7 2 50 15

5 3 9 1 14 19 4

Вы расшифровали части шифровки, а теперь давайте сложим запись целиком. Что получили?

ЗАКОНЫ СЛОЖЕНИЯ

Итак, тема нашего урока – Законы сложения

Посмотрим на доску:

1. 2.

5+3 = 3+5 (3+5)+2=3+(5+2)

9+2 = 2+9 (2+7)+3=2+(7+3)

-Чем интересны эти выражения? Что вы в них видите необычного?

-Знак равенства, одинаковые слагаемые с каждой стороны.

-Что изменяется в записях?

-Порядок слагаемых, скобки.

-Как вы думаете, что мы сегодня на уроке должны доказать, узнать? Какая задача стоит перед нами?

-Мы должны узнать почему стоит знак равенства, доказать, что складывать числа можно в любом порядке.

Давайте откроем учебник и прочитаем нашу задачу на урок. Страница 44.

Итак, что мы должны сделать на этом уроке?

-Мы должны доказать, что числа можно складывать в любом порядке.

-Мы познакомимся с законами сложения и научимся их применять при решении выражений и задач.

4.Подготовка к изучению нового материала. Актуализация знаний.

Можно ли сказать, что все записи на доске вам не знакомы, может быть, один из законов сложения вы знаете?

-Да, мы знаем 1 закон сложения.

Как он звучит?

-От перестановки слагаемых сумма не меняется.

В каких случаях и для чего его удобно применять?

-Когда первое слагаемое меньше второго. К большему числу легче прибавлять меньшее.

Давайте поупражняемся в применении этого закона. Посмотрите на выражения, запишите их рационально, т.е. удобно и вычислите.

1+17=17+1 4+10=10+4

2+9=9+2 3+16=16+3

Проверка и оценка первых 3 человек, сделавших первыми.

Проверка фронтально. Один ученик читает свой вариант, класс анализирует, получилось ли вычислить рационально. Самооценка.

У кого получилось выполнить рационально?

Посмотрите на запись выражений. Что происходит со слагаемыми?

-Они меняются местами.

То есть слагаемые перемещаются, поэтому этот закон называется ПЕРЕМЕСТИТЕЛЬНЫЙ.

5.Изучение нового материала

А теперь обратимся к выражениям второго столбика и познакомимся со вторым законом сложения.

Может быть, вы сможете объяснить, почему верны эти записи?

(3+5)+2=3+(5+2)

(2+7)+3=2+(7+3)

Посмотрите, чем отличаются эти выражения, от выражений первого столбика?

-3 слагаемых

А что происходит со слагаемыми?

-Они сгруппированы по-разному.

Может быть, кто-нибудь сможет сделать вывод?

Давайте попросим наш компьютер помочь нам сформулировать это закон.

1.Смотрим первый сюжет про шарики до конца.

4+2+3=4+2+3

Как считали мальчики?

-Петя (4+2)+3 Паша 4+(2+3).

Что они делали по-разному?

-Они по-разному группировали шарики.

Почему можно по-разному группировать шарики?

-Потому что сумма шариков остается неизменной.

Может быть, вы сможете сформулировать закон сложения?

-Слагаемые можно группировать по-разному.

Правильно слагаемые можно группировать или по-научному СОЧЕТАТЬ по-разному. Может быть,скажете как называется это закон? СОЧЕТАТЕЛЬНЫЙ.

2.Смотрим второй сюжет и попробуем закончить самостоятельно.

Зачитывается только условие, у вас на партах листочки с этим заданием, попробуйте сосчитать мячи по-разному, применив сочетательный закон.

На доске: 2+1+4=2+1+4

Ученик выходит и расставляет скобки в выражениях, в соответствии с сочетательным законом. Что мы с вами делали?

-Группировали или сочетали слагаемые по-разному.

Получали ли мы одинаковую сумму? –Да.

Кто может сформулировать сочетательный закон?

Слагаемые можно группировать по-разному.

Давайте проверим по компьютеру, правильно ли мы сосчитали мячи. Досматриваем сюжет до конца.

А теперь нам нужно разобраться, зачем нам нужен этот закон сложения.

Посмотрите на выражения, давайте их решим:

Запись в тетради.

9+7+1=(9+1)+7

8+9+2+1=(8+2)+(9+1)

7+1+2+9+3=(7+3)+(9+1)+2

Сначала решаем так, как написано, а затем с применением сочетательного закона. Выясняем, что при применении сочетательного закона, считать легче и быстрее. Делаем вывод: законы сложения нужны для того, чтобы легче было считать.

Давайте посмотрим, что скажет наш компьютер, и прочитаем вывод в учебнике на странице 44.

Физминутка.

6.Первичное закрепление знаний

Откройте Рабочую тетрадь стр.35 №21(2)

Запишем эти выражения в тетрадь и вычислим по-разному:

1. так как написано

2.с применением переместительного закона

3. с применением сочетательного закона

6+7+4+3=6+4+7+3=(6+4)+(7+3)

Выполняем столько выражений, сколько успеем.

Итог:

Что мы научились делать?

-Рационально, удобно считать.

С какими законами сложения познакомились?

-С переместительным и сочетательным.

Сформулируйте эти законы.

От перестановки слагаемых сумма не меняется.

Слагаемые можно группировать (сочетать) по-разному.

Вы будете пользоваться этими законами на протяжении всей жизни, они помогают быстро считать.

Как вы думаете, можно ли применить эти законы при решении задачи? –да.

Давайте попробуем.

7.Работа над задачей

Страница 45, №5.

Найдите периметр прямоугольника со сторонами 30 мм и 20 мм.

Что нам нужно вспомнить для решения этой задачи?

-Что такое периметр. Это сумма длин всех сторон.

Как найти периметр четырехугольника?

-Нужно сложить длины всех сторон.

Запишем решение:

30+20+30+20=

Применим законы сложения. Выберите сами, как вам удобно считать.

Проверяем, ученики читают свои решения и называют примененный закон.

Что еще нам нужно сделать?

-Выразить ответ в см. 100мм=10см

Запишем ответ: периметр равен 10 см.

8.Итог урока, домашнее задание

С какими законами познакомились?

-Переместительным и сочетательным.

Сформулируйте эти законы.

Зачем нам нужно знать законы сложения?

Где можно применять эти законы?

Дома вы выучите правила на странице 44, закончите № 21 по рабочей тетради так, как делали в классе.

9.Рефлексия.

Те ребята, кто считает, что очень хорошо поработал на уроке и все понял, поднимите красную полоску, кто считает, что еще не очень хорошо разобрался – зеленую.

Мы с вами еще будем работать с этими законами и даже если сегодня не все получилось, обязательно получится на следующих уроках.

Коммутативные, ассоциативные и дистрибутивные законы

Вау! Какой набор слов! Но идеи простые.

h2zsWdHC_V8

Коммутативные законы

«Законы коммутации» говорят, что мы можем поменять местами числа и все равно получить тот же ответ…

… когда мы добавляем :

а + б = б + а

Пример:

… или когда мы умножить :

а × б = б × а

Пример:

Проценты тоже!

Поскольку a × b = b × a, также верно, что:

а% от б = б% от

Пример: чему равно 8% от 50?

8% от 50 = 50% от 8
= 4

Почему «коммутативный » … ?

Потому что числа могут двигаться вперед и назад, как пригородный .

4591, 4599, 4615, 4639, 4647, 4592, 4600, 4616

КБфнкУГЭМВИ

Ассоциативные законы

«Ассоциативные законы» говорят, что не имеет значения, как мы группируем числа (т. е. какие мы вычисляем первыми)…

… когда мы добавляем :

(а + б) + в = а + (б + в)

… или когда мы умножаем :

(а × б) × в = а × (б × в)

Примеры:

Это:	(2 + 4) + 5 = 6 + 5 = 11
Имеет тот же ответ, что и этот:	2 + (4 + 5) = 2 + 9 = 11

Это:	(3 × 4) × 5 = 12 × 5 = 60
Имеет тот же ответ, что и этот:	3 × (4 × 5) = 3 × 20 = 60

Использование:

Иногда проще складывать или умножать в другом порядке:

Сколько будет 19+36+4?

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

Или немного переставить:

Что такое 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

4603, 4610, 4627, 4631, 4643, 4654, 4606, 4612

0v-G6OwcKmU

Распределительный закон

«Распределительный закон» — САМЫЙ ЛУЧШИЙ из всех, но требует особого внимания.

Вот что он позволяет нам делать:

3 партии (2+4) то же, что и 3 партии 2 плюс 3 партии по 4 шт.

Итак, 3× можно «распределить» по 2+4 , на 3×2 и 3×4

А пишем так:

a × (b + c) = a × b + a × c

Попробуйте посчитать сами:

3 × ( 2 + 4 ) = 3 × 6 = 18
3×2 + 3×4 = 6 + 12 = 18

В любом случае ответ один.

По-английски мы можем сказать:

Мы получим тот же ответ, если:

умножим число на группу чисел, сложенных вместе или
сделать каждый умножить отдельно, затем добавить их

Использование:

Иногда бывает проще разбить сложное умножение:

Пример: Что такое 6 × 204?

6 × 204 = 6 × 200 + 6 × 4
= 1200 + 24
= 1224

Или комбинировать:

Пример: Сколько будет 16 × 6 + 16 × 4?

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Мы можем использовать его и при вычитании:

Пример: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

Мы могли бы использовать его и для длинного списка дополнений:

Пример: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6 ×7 + 2 ×7 + 3 ×7 + 5 ×7 + 4 ×7
= (6+2+3+5+4) × 7

= 290 × 7
= 140

5656, 5657, 5658, 5659, 5660, 5661, 3172

Таковы Законы.

. .

. . . но не заходите слишком далеко!

Коммутативный закон выполняет , а не работу для вычитания или деления:

Пример:

12/3 = 4 , но
3 / 12 = =

Ассоциативный закон заставляет , а не работать для вычитания или деления:

Пример:

(9 – 4) – 3 = 5 – 3 = 2 , но
9 – (4 – 3) = 9 – 1 = 8

Распределительный закон делает , а не работой для деления:

Пример:

24 / (4 + 8) = 24 / 12 = 2 , но
24/4 + 24/8 = 6 + 3 = 9

Резюме

Коммутативные законы:	a + b = b + a a × b = b × a
Ассоциативные законы:	(a + b) + c = a + (b + c) (a × b) × c = a × (b × c)
Распределительное право:	a × (b + c) = a × b + a × c

Деятельность: Коммутативная, Ассоциативная и Распределительная

Коммутативный закон — значение, законы сложения, умножения и множества

В математике коммутативный закон имеет дело с арифметическими операциями сложения и умножения. Однако он не используется для двух других арифметических операций, вычитания и деления. Давайте определим коммутативный: «Коммутативный» происходит от слова «коммутировать», которое можно определить как передвигаться или путешествовать. Согласно коммутативному закону или коммутативному свойству. Если a и b — любые два целых числа, сложение и умножение a и b дает один и тот же результат независимо от положения a и b. Это можно представить символически как:

a + b = b + a

a × b = b × a

Например, если 5 и 10 — два числа, то;

5 + 10 = 10 + 5 = 15

5 х 10 = 10 х 5 = 50

Что такое коммутативное право?

Закон коммутации гласит, что при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Или, другими словами, последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.

Объясним коммутативный закон

Итак, математически, если изменение порядка операндов не влияет на результат арифметической операции, эта арифметическая операция является коммутативной.

Предположим, что А и В — два действительных числа, тогда согласно этому закону;

А + В = В + А

А . Б = Б . A

Коммутативный закон сложения

Согласно коммутативному закону сложения, при сложении двух чисел результат равен сумме их переставленных позиций.

A + B = B + A

Примеры:

1 + 2 = 2 + 1 = 3

4 + 5 = 5 + 4 = 9

-3 + 6 = 6 + (-3) = 6 — 3 = 3

Этот закон неприменим к вычитанию, потому что если первое число отрицательное и положение меняется, знак первого числа меняется на положительный, в результате чего:

(-A) — B = -A – B ……(1)

Когда мы меняем положение первого и второго числа, мы получаем;

B — (-A) = B + A …. (2)

В результате уравнений 1 и 2 получаем:

(-A) — B ≠ B — (-A)

Например: (-9) — 2 = -9 — 2 = -11

& 2-(-9) = 2 + 9 = 11

Следовательно, -11 ≠ 11.

Коммутативный закон умножения

Согласно коммутативному закону умножения, результат умножения двух чисел останется тем же самым, даже если числа поменять местами.

Следовательно, A . Б = Б . A

Примеры:

1 × 2 = 2 × 1 = 2

4 × 5 = 5 × 4 = 20

-3 × 6 = 6 × (-3) = -18

Почему умножение коммутативно?

Давайте посмотрим на пример, чтобы понять.

У нас есть математическая формула, которая говорит то же самое. Это выглядит следующим образом:

a * b = b * a

Разные буквы обозначают разные числа. Обратите внимание, что у нас есть a * b слева от символа равенства, в то время как b идет первым справа от знака равенства. В результате эта формула также говорит нам, что последовательность, в которой мы умножаем наши числа, не имеет значения. Тем не менее, мы получаем тот же ответ.

Несмотря на то, что эта формула показывает только два числа, переместительное свойство умножения также применяется, когда вы умножаете более двух чисел. Когда имеется более двух чисел, мы можем расположить их в любом порядке. Например, предположим, что у нас есть:

3 * 5 * 2

Мы можем изменить его на 3 * 2 * 5 или 5 * 3 * 2. Мы получим один и тот же ответ в любом случае.

Отсюда можно сказать, что умножение коммутативно.

Коммутативное право в процентах

Если мы поменяем местами или поменяем порядок значений при вычислении процентов, результат останется прежним. Математически мы можем сказать:

A% от B = B% от A

Пример:

10% от 50 = 50% от 10

Так как

10% от 50 можно записать как (10/100 ) x 50 = 5

50% от 10 можно записать как (50/100) x 10 = 5

Таким образом, ответ остается прежним.

Коммутативный закон множеств

Термин «набор» относится к группе элементов или объектов. Мы изучили многочисленные типы операций, которые можно выполнять над множествами, такие как пересечение, объединение и разность.

Согласно коммутативному закону объединения множеств и коммутативному закону пересечения множеств

последовательность множеств, в которых выполняются операции, не влияет на результат.

Если A и B два различных множества, то, согласно правилу перестановки,

A ∪ B = B ∪ A [представляет объединение множеств]

[Изображение будет загружено в ближайшее время]

A ∩ B = B ∩ A [Обозначает пересечение наборов]

[Изображение будет загружено в ближайшее время]

Рассмотрим пример, если A = {1, 2, 3} и B = {3, 4, 5, 6}, тогда;

A Union B представлен как A ∪ B {1, 2, 3, 4, 5, 6} …….. (i)

B Union A представлен как B ∪ A {1, 2, 3, 4 , 5, 6} ……… (ii)

Из (i) и (ii) получаем;

A ∪ B = B ∪ A

Теперь,

Пересечение B представлено как A ∩ B = {3} ……. .(iii)

B пересечение A представлено как B ∩ A = {3} ……..(iv)

Из (iii) и (iv) получаем;

A ∩ B = B ∩ A

В результате был установлен коммутативный закон объединения и пересечения двух множеств.

Заключение

Мы уже обсуждали закон перестановочности в математике, свойство перестановочности гласит, что «изменение порядка операндов не меняет результат. Мы видели, что свойство перестановочности применимо только к умножению и сложению. следуйте коммутативному свойству.

Коммутативное свойство сложения – формула, применение, примеры

Коммутативное свойство сложения гласит, что сумма двух или более чисел остается неизменной независимо от того, как они сгруппированы. Давайте узнаем больше о коммутативном свойстве сложения в этой статье.

1.	Что такое коммутативное свойство сложения?
2.	Коммутативное свойство формулы сложения
3.	Применение коммутативного свойства Дополнения
4.	Часто задаваемые вопросы о коммутативном свойстве сложения

Что такое коммутативное свойство сложения?

Согласно коммутативному свойству сложения, если два или более числа сложить или суммировать, мы получим один и тот же результат независимо от того, как числа сгруппированы. Здесь группировка относится к представлению, в котором скобки размещены и расположены в данной задаче сложения. Обратите внимание на следующий пример, чтобы понять концепцию коммутативного свойства сложения.

5 + 6 = 6 + 5
11 = 11

Здесь мы можем ясно видеть, что когда мы, наконец, складываем все числа с различным расположением, результирующая сумма одинакова.

Коммутативное свойство формулы сложения?

Свойство коммутативности говорит о том, что порядок операндов не меняет окончательный результат. Формула коммутативного свойства для сложения приведена ниже.

Коммутативное свойство формулы сложения

Коммутативное свойство формулы сложения : Переместительное свойство сложения говорит о том, что порядок, в котором мы складываем слагаемые, не меняет сумму.

А + В = В + А

Применение коммутативного свойства дополнения

Коммутативный закон сложения применим только тогда, когда мы можем получить желаемый результат равным в любом требуемом расположении, т. е. LHS = RHS. Попробуем обосновать, как и почему свойство коммутативности справедливо только для умножения и сложения. Мы применим общий закон коммутативной собственности индивидуально к четырем основным операциям. Далее мы обсудим реальное приложение, чтобы лучше понять коммутативное свойство умножения.

Для сложения : Коммутативное свойство для сложения выражается как a + b = b + a. Например, (17 + 4) = (4 + 17) = 21. Мы говорим, что сложение коммутативно для данного набора чисел.

Для умножения : Коммутативное свойство умножения задается как A × B = B × A. Например, (17 × 4) = (4 × 17) = 68. Здесь мы находим, что умножение является коммутативным для данного набора чисел.

Давайте посмотрим на реальное приложение, основанное на коммутативном свойстве сложения.

Иллюстрация: Есть семь гамбургеров и пять пицц. Найдите общее количество предметов, используя переместительное свойство сложения для обратных комбинаций, которые вы можете купить.

Решение: Из 7 бургеров вы можете выбрать 5 пицц, что даст вам комбинацию 7 + 5 = 12 предметов.
Также с 5 пиццами вы можете выбрать 7 бургеров, эта комбинация дает вам 5 + 7 = 12 предметов.
Обе комбинации описывают коммутативное свойство сложения между 7 гамбургерами и 5 пиццами.

Давайте рассмотрим несколько примеров, чтобы лучше понять коммутативное свойство сложения.

Примеры коммутативного свойства сложения

Пример 1: Если (6 + 4) = 10, то докажите, что (4 + 6) также дает 10, используя свойство перестановочности формулы сложения
Решение:
Поскольку сложение удовлетворяет свойству перестановочности
Отсюда (6 + 4) = (4 + 6) = 10,
.
Пример 2: Мать Эрика спросила его, является ли p + q = q + p примером коммутативного свойства сложения. Можете ли вы помочь Эрику выяснить, является ли оно коммутативным или нет?
Решение:
Мы знаем, что свойство перестановочности умножения гласит, что изменение порядка слагаемых не изменит значения суммы.
р+д = д+р
Итак, мы видим, что изменение порядка не изменит значения суммы.
Итак, это пример коммутативного свойства сложения.
Ответ: p + q = q + p — пример коммутативного свойства сложения.

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Забронировать бесплатный пробный урок

Практические вопросы

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коммутативном свойстве сложения

Что такое закон сложения мутативной собственности?

Формула коммутативного свойства для сложения определяется как t сумма двух или более чисел, которые остаются одинаковыми, независимо от порядка операндов и слагаемых. Кроме того, формула коммутативного свойства выражается как (A + B) = (B + A).

Как найти коммутативное свойство сложения?

Коммутативное свойство сложения утверждает, что если ‘a’ и ‘b’ — два числа, то a + b = b + a. Можно проверить, равны ли левые и правые члены после решения заданных числовых значений.

Что является примером коммутативного свойства сложения?

Пример коммутативности сложения: (A + B) = (B + A). Здесь A = 8 и B = 9. При решении получаем 8 + 9 = 9 + 8 = 17. Отсюда доказано, что LHS равно RHS.

Каким будет свойство коммуникативности сложения чисел 7 и 6?

Расположим данные числа согласно общему уравнению коммутативного закона, то есть (A + B) = (B + A). Здесь A = 7 и B = 6. При решении получаем 7 + 6 = 6 + 7 = 13. Отсюда доказано, что LHS равно RHS.

Что такое коммутативное свойство сложения рациональных чисел?

Коммутативное свойство сложения для рациональных чисел может быть выражено как (P + Q) = (Q + P). Здесь значения P, Q представлены в виде a/b, где b ≠ 0,

Что такое коммутативное свойство сложения дробей?

Переместительное свойство сложения дробей можно выразить как (P + Q) = (Q + P). Здесь значения P, Q представлены в виде a/b. Например, допустим, P = 7/8 и Q = 5/2. Подставляя значения в (P + Q) = (Q + P), мы получаем (7/8 + 5/2) = (5/2). + 7/8) = 27/8.

Что такое коммутативное свойство сложения целых чисел?

Переместительное свойство сложения целых чисел может быть выражено как (P + Q) = (Q + P). Например, допустим, P = -3 и Q = -9при подстановке значения в (-3 + (-9)) = (-9 + (-3)) = -12. Следовательно, левая сторона = правая сторона.

Скачать БЕСПЛАТНЫЕ учебные материалы

Коммутативное свойство сложения. Рабочие листы

Сложение, умножение, доказательство и решенные примеры

Жасмин Гровер

Старший специалист по содержанию | Обновлено 12 мая 2022 г.

Коммутативный закон касается арифметических операций сложения и умножения. Коммутативный закон не используется для двух других арифметических действий, вычитания и 9.0610 отдел . Если мы определяем коммутативный, термин «коммутативный» происходит от слова «коммутировать», которое можно определить как перемещение или путешествие. Коммутативный закон или коммутативное свойство объясняет, что если «a» и «b» — любые два целых числа, сложение и умножение «a» и «b» дают один и тот же результат независимо от их положения. Мы можем символически представить это как: (a + b = b + a) и (a × b = b × a).

Содержание

Что такое коммутативное право?
Proof of Commutative Law
Things to Remember
Sample Questions

Key Terms: Commutative Law, Arithmetic Operations, Addition, Multiplication, Associative Law, Subtraction, Division , Процент

Что такое коммутативное право?

[Нажмите здесь, чтобы просмотреть примеры вопросов]

В соответствии с законом коммутативности при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Проще говоря, последовательность, в которой мы складываем или умножаем любые два действительных чисел не влияет на результат. Следовательно, если изменение порядка операндов не влияет на результат арифметической операции, эта арифметическая операция является коммутативной.

Если принять во внимание, что А и В — два действительных числа, то по этому закону;

A + B = B + A
A x B = B x A

Например, если 50 и 100 — два целых числа, то;

50 + 100 = 100 + 50 = 150

50 x 100 = 100 x 50 = 5000

Подробнее: Умножение и разделение целых чисел

Доказательство законодательства о коммутативном законодательстве

было доказано ниже.

Переместительный закон сложения

Согласно переместительному закону сложения, если сложить два числа, то результат равен сложению их переставленных позиций.

A + B = B + A

Примеры:

1 + 2 = 2 + 1 = 3
4 + 5 = 5 + 4 = 9
-3 + 6 = 6 + (-3 ) = 6 –
3 = 3

Закон коммутации неприменим для вычитания, потому что если первое число отрицательное и если мы изменим положение, то знак первого числа изменится на положительный, следовательно;

(-А)-В=-А-В……(1)

После изменения положения первого и второго числа получаем;

В – (-А) = В + А…. (2)

Следовательно, из уравнений 1 и 2 мы можем видеть, что;

(-A) — B ≠ B — (-A)

Например: (-9) — 2 = -9 — 2 = -11 и 2 — (-9) = 2 + 9 = 11

Отсюда , -11 ≠ 11.

Коммутативный закон о добавлении

Читать Дальнейшие: Дополнение и вычитание целых чисел

Законодательство о размножении 9029

9 СПКАТИЕ СЛЕДУ. умножение двух чисел остается прежним, даже если положения чисел меняются местами.
Следовательно, A x B = B x A
Примеры:
1 × 2 = 2 × 1 = 2
4 × 5 = 5 × 4 = 20
-3 × 6 = 6 ( -3) = -18
Коммутативный закон о умножении
Читать Дальнейшие: Умножение и деление
. поменять порядок значений, затем
ответ не меняется. Математически мы можем сказать;
A% от B = B% от A
Пример:
20% от 50 = 50% от 20 50% от 20 = (50/100) х 20 = 10
Таким образом, ответ остается прежним.
Подробнее: Как рассчитать процент?
Что нужно помнить
Коммутативный закон объясняет, что последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.
Когда мы складываем или умножаем два числа, конечное значение остается одним и тем же независимо от положения двух чисел.
Возьмем A и B два действительных числа, тогда по коммутативному закону; A + B = B + A и A x B = B x A
Коммутативный закон неприменим для вычитания, потому что если первое число отрицательное и если мы изменим положение, то знак первого числа изменится на положительный .
Закон коммутативности не применим к делению, потому что замена значений даст разные результаты, a / b не равно b / a.
Примеры вопросов
Вопросы. Укажите разницу между коммутативным свойством и ассоциативным свойством? (5 баллов)
Отв. Свойство коммутативности говорит о том, что изменение порядка чисел в операции сложения или умножения не меняет сумму или произведение.
Для сложения коммутативность: A + B = B + A.
Для умножения коммутативность: A × B = B × A.
Принимая во внимание, что ассоциативное свойство утверждает, что сложение или умножение двух или более целых чисел без их группировки или объединения не изменяет сумму или результат.
Представим ассоциативное свойство сложения как: (А + В) + С = А + (В + С).
Ассоциативное свойство умножения: (A × B) × C = A × (B × C).
Вопрос. Дайте определение коммутативному закону. (3 балла)
Отв. Согласно закону коммутативности при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Проще говоря, последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.
Вопрос. Приведите пример коммутативного закона сложения? (1 балл)
Отв. Пример коммутативного закона сложения: 40 + 10 = 10 + 40 = 50
Ques. Приведите пример коммутативного закона умножения? (1 балл)
Отв. Пример коммутативного закона умножения: 2 x 5 = 5 x 2 = 10
Ques. Можем ли мы использовать переместительное свойство для вычитания и деления? (3 балла)
Ответ. Мы не можем использовать свойство коммутативности для вычитания и деления, потому что, когда мы меняем порядок чисел при выполнении вычитания и деления, мы получаем разные результаты.
Например, когда мы вычитаем (5 — 2) равно 3, тогда как вычитание (3 — 5) не равно 3. Точно так же, когда 10 делится на 2, это дает 5, тогда как, когда 2 делится на 10 не дает 5. Таким образом, мы можем сказать, что свойство коммутативности неверно для вычитания и деления.
Вопрос. Приведите пример коммутативного закона в процентах. (3 балла)
Отв. 10% от 50 = 50% от 10
Поскольку
10% от 50 можно записать как (10/100) x 50 = 5
50% от 10 можно записать как (50/100) x 10 = 5
Таким образом, мы замечаем, что результат остается прежним.
Вопросы. Приведите пример перестановочного закона множеств. (3 балла)
Отв. Даны A = {1, 2, 3} и B = {3, 4, 5, 6}
Пусть A ∪ B {1, 2, 3, 4, 5, 6} ……. . (i)
Таким образом, B ∪ A {1, 2, 3, 4, 5, 6} ……… ( ii)
Из (i) и (ii) мы получаем;
A ∪ B = B ∪ A
Теперь
Пересечение B представлено как A ∩ B = {3} ……. (iii)
B пересечение A представлено как B ∩ A = {3} ……. (iv)
Из (iii) и (iv) получаем;
A ∩ B = B ∩ A
Таким образом, закон перестановочности для объединения и пересечения двух множеств установлен.
Вопрос. Дано, A = 25 и B = 20. Объясните перестановочный закон сложения, перестановочный закон умножения и перестановочный закон в процентах с одинаковыми значениями A и B. (3 балла)
Ответ. A) Для коммутативного закона сложения: A = 25, B = 20
A + B = 25 + 20 = 45. Кроме того, B + A = 20 + 25 = 45.
Следовательно, A + B = B + A
B) Для коммутативного закона умножения: A = 25, B = 20
A x B = 25 x 20 = 500. Кроме того, B x A = 20 x 25 = 500.
Следовательно, A x B = B x A
C) Для коммутативного закона процентов: A = 25, B = 20
A % от B = 25 % от 20 = 5
B % от A = 20 % of 25 = 5
Следовательно, A % от B = B % от A.
Проверить:
Что такое коммутативное свойство сложения? Определение, примеры
Сложение — это первый арифметический оператор, о котором учащиеся узнают при изучении элементарной математики. Сложение, как следует из названия, является простой темой, а также закладывает основу для умножения и некоторых многозначных арифметических операций. Одним из очень интересных свойств сложения является коммутативность.
Возьмем пример.
Предположим, у вас есть 3 яблока и 2 апельсина.
Как найти общее количество фруктов, которые у вас есть?
Сложите 3 и 2 и получите 5.
Но как вы думаете, получился бы другой ответ, если бы мы взяли сначала апельсины, а потом яблоки?
Нет, общее количество фруктов осталось прежним. Это 5.
И это интересное свойство коммутативности для сложения.
Что такое коммутативное свойство сложения?
«Коммутировать» означает путешествовать или передвигаться. Переместительное свойство сложения гласит, что изменение порядка слагаемых чисел не влияет на сумму. Мы можем определить коммутативное свойство сложения, так как сложение чисел в любом порядке даст один и тот же ответ.
Здесь a и b могут быть целыми, целыми, десятичными и даже дробными числами.
Коммутативное свойство сложения Примеры:
15 + 16 = 16 + 15 = 31
4 + (–6) = (–6) + 4 = (–2)
0,5 + 0,6 = 0,6 + 0,5 = 1,1
$\frac{1} {5}$ $+$ $\frac{2}{5}$ $=$ $\frac{2}{5}$ $+$ $\frac{1}{2}$ $=$ $\frac{ 3}{5}$
Соблюдают ли другие операторы закон коммуникативности?
Не совсем так. Закон коммутативности можно применить только к понятиям сложения и умножения.
Допустим, мы хотим решить выражение 3 умножить на 4 или 3 ✕ 4.
Мы можем просто пропустить счет на 4 три раза, и мы получим 12.
Точно так же мы можем найти впадину 4 умножить на 3 или 4 ✕ 3, и мы снова получим 12.
Итак, изменение порядка умножения чисел на самом деле не изменило произведение.
Следовательно, умножение подчиняется закону коммутативности.
Однако, если мы говорим о вычитании, изменение порядка чисел в уравнении вычитания абсолютно изменит результат. Давайте разберемся с этим на примере.
Вычтем 3 из 4.
4 – 3 = 1
Теперь, если мы изменим порядок чисел,
3 – 4 = (-1)
Ну, числа не обязаны со всем соглашаться все время, да?
Деление, будучи самым капризным из всех наших операторов, которому нужно помнить так много, не следует закону коммутативности.
Решенные примеры
Пример 1. Проверьте, что «a + b = b + a», если a = 33 и b = 30.
Решение:
Подстановка значений в левой части уравнения,
a + b = 33 + 30 = 63
Подстановка значений в правой части уравнения,
b + a = 30 + 33 = 63
Таким образом, проверяется, что a + b = b + a.
Пример 2: Заполните заготовки:

20 + _ = _ + 20 = 55
. 0611
Поскольку результат тот же, уравнение должно обладать свойством коммутативности.
Итак, пропущенное число можно представить как «b».
Теперь у нас есть
20 + b = 55,
Следовательно, b = 55 – 20 = 35.
Пример 3. Докажите на примере, почему вычитание неприменимо к закону коммутативности?
Решение: Возьмем два числа: 3 и 5 .
Если из 5 вычесть 3, то получится 2 .
Но если мы обратим порядок и вычтем 5 из 3 , , мы получим результат как – 2 .
Следовательно, свойство коммутативности не применяется к вычитанию, так как изменение порядка меняет ответ.
Пример 4: Какая из следующих дробей демонстрирует свойство коммутативности с $\frac{1}{3}$ $+$ $\frac{1}{2}$ ?
$\frac{1}{2}$ $\times $ $\frac{1}{3}$
$\frac{1}{3}$ $\div$ $\frac{1} {2}$
$\frac{1}{2}$ $+$ $\frac{1}{3}$
$\frac{1}{3}$ $-$ $\frac{1}{2}$
Решение: (c) $\frac{1}{2}$ $+$ $\frac{1}{3}$
По закону коммутативности сложения , $\frac{1}{ 2}$ $+$ $\frac{1}{3}$ даст тот же результат, что и $\frac{1}{3}$ $+$ $\frac{1}{2}$.
Практические задачи
42
67
39
81
Правильный ответ: 67
Используя свойство перестановочности сложения,
a + b = b + a,
Следовательно, 39 + 67 = 67 + 39,
Следовательно, недостающее число равно 67.
c = a +b
a (b + c) = a ✕ b + b ✕ c
a + b = b + a
a + (b+c) = a+c
Правильный ответ: a + b = b + a
Закон кумулятивности утверждает, что в уравнении сложения изменение порядок чисел по-прежнему дает тот же результат.
Следовательно, а + b = b + а.
23
26
25
27
Правильный ответ: 25
Поскольку результат тот же, уравнение должно следовать свойству коммутативности.
Таким образом, мы можем представить пропущенное число как «b».
Теперь мы имеем
23 + B = 48,
Следовательно, B = 48 — 23 = 25.
5.009
5,990
3,789
1,22
Правильный ответ: 5,009
по закону коммутативности добавления, 1,22222222222. + 3,789 = 3,789 + 1,22 = 5,009
Часто задаваемые вопросы
Применяется ли свойство перестановочности сложения к дробям?
Да, согласно коммутативному свойству сложения, a + b = b + a для любых чисел a и b.
Существует ли коммутативное свойство для вычитания?
Нет, операции вычитания и деления не подчиняются законам коммутативности.
Каковы свойства операции сложения?
Три свойства сложения являются коммутативными: для любых двух чисел a и b, a + b = b + a.
Ассоциативное свойство: Для любых трех чисел a, b и c, a + (b + c) = (a + b) + c.
Свойство идентичности: для каждого числа a, a + 0 = a.
Узнайте о переместительном законе сложения
Переместительный закон сложения Определение
Согласно этому закону, две величины при сложении дают один и тот же результат независимо от порядка их сложения. A+B=B+A{\ rm{A + B = B + A}}A+B=B+A
Обзор коммутативного закона сложения
Коммутативный происходит от французского слова «пригородный», что означает замещать. Он удачно используется для описания тех свойств, которые дают тот же результат после перемещения по кругу. элементы. Сейчас мы сосредоточимся на коммутативном законе сложения. Проще говоря, это просто означает, что два элемента могут быть добавлены в любом порядке и давать одинаковый результат.
Например,
1+4=4+1=51 + 4 = 4 + 1 = 51+4=4+1=5
−51+40=40−51=−11 — 51 + 40 = 40 — 51 = — 11−51+40=40−51=−11
Следует отметить, что до сих пор мы воздерживались от использования слова «числа». Это потому, что коммутативный закон не применяется только к действительным числам. Он относится к сложным системы, матрицы и векторы.
Например,
a⃗+b⃗=b⃗+a⃗=c⃗\vec a + \vec b = \vec b + \vec a = \vec ca+b=b+a=c
z + w = w + zz {\ rm { }} + {\ rm { }} w {\ rm { }} = {\ rm { }} w {\ rm { }} + {\ rm { }} zz +w=w+z, где z=x1+iy1z{\rm{ }} = {\rm{ }}{x_1} + {\rm{i}}{y_1}z=x1+iy1 и w= x2+iy2w{\rm{ }} = {\rm{ }}{x_2} + {\rm{ i}}{y_2}w=x2+iy2 (Комплексные числа)
Переместительный закон сложения является основным законом, который применяется ко многим системам в математике. На первый взгляд это может показаться очевидным, но для систем, включающих векторы или матрицы, это не является естественным выводом.
В течение многих столетий свойство коммутативности неявно предполагалось правильным. Только в конце и начале века, когда наука и математика стали более формализованными, свойство коммутативности впервые стало явно формулироваться.
Есть вопрос по этой теме?
Что вы изучите:
Определение переместительного закона сложения
Обзор переместительного закона сложения
Переместительное свойство векторов
Коммутативный закон матриц
Коммутативный закон умножения
Коммутативное свойство векторов
Вектор – это величина, которая обладает как величиной, так и направлением. Обычно он изображается линией, где длина линии представляет его величину, а стрелка указывает направление вектора.
Векторы, как и числа, обладают свойством коммутативности.
Чтобы объяснить свойство коммутативности векторов, мы возьмем пример двумерного векторы.
Допустим, парк имеет форму параллелограмма OAPB, как показано ниже.
Рис.1.1 Парк в форме параллелограмма
Нам нужно попасть в точку P из точки O.
Независимо от того, выберем ли мы путь OBP или путь OAP, перемещение OP останется одним и тем же.
Рис.1.2. Путь OP, соединяющий точки O и P
В этом смысл коммутативного закона сложения векторов.
Если мы рассмотрим OB=AP=a⃗OB = AP = \vec aOB=AP=a и OA=BP=b⃗OA = BP = \vec bOA=BP=b и OP=c⃗OP = \vec cOP=c , тогда коммутативный закон дополнения гласит, что:
a⃗+b⃗=b⃗+a⃗=c⃗\vec a + \vec b = \vec b + \vec a = \vec ca+b=b+a=c
Рис. 1.3. Коммутативный закон, использующий сложение векторов
Хотя здесь мы использовали двумерные векторы, это применимо и к трехмерным векторам.
Коммутативный закон матриц
Матрица представляет собой расположение чисел в строках и столбцах прямоугольной формы. Размеры матрицы записываются в виде n x m, где n — количество строк, а m это количество столбцов.
Например, имеет две строки и три столбца, поэтому это матрица 2 X 3 .
Матрицы широко используются для построения графиков и представления данных, включая векторы, поэтому Важно знать их основные свойства, чтобы иметь возможность их использовать.
Чтобы добавить две матрицы, мы добавляем элементы, занимающие одинаковые позиции в соответствующих матрицах.
Однако можно добавлять только матрицы одинакового размера. Мы не можем добавить матрицу размерности 2 X 3 к матрице размерности 1 X 3 или 3 X 2.
Теперь, когда мы знаем, как складывать матрицы, мы можем перейти к доказательству их коммутативности.
Пусть A и B — две матрицы 3 X 2 такие, что:
Таким образом, мы показали, что матрицы коммутативны.
Коммутативный закон умножения
Коммутативный закон сложения — один из многих основных законов, распространенных в математике. Другим подобным законом является коммутативный закон умножения.
Согласно этому закону порядок умножения двух величин не влияет на конечный продукт.
То есть
A×B=B×A{\rm{A}} \times {\rm{B}} = {\rm{B}} \times {\rm{A}}A×B =B×A
Однако этот закон не так универсален, как закон сложения. Это верно для действительных чисел, но это оказывается ложным применительно к матрицам и перекрестному произведению векторов.
Это следует из того, что умножение матриц упорядочено. Мы можем умножить только два матрицы, если количество столбцов одной матрицы равно количеству строк второй матрицы.