Правила умножения и деления | Дефектология Проф
После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.
ЧТО ТАКОЕ УМНОЖЕНИЕ? ЭТО УМНОЕ СЛОЖЕНИЕ
При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:
- 5 × 3 = 15;
- 86 – 9 = 77;
- 81 : 9 = 9.
В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.
ДА КАКАЯ РАЗНИЦА?
Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?
- Рассмотрим примеры:
10 – 5 + 2 = ?
Если мы будем выполнять действия по порядку, получим:
- 10 – 5 = 5;
- 5 + 2 = 7.

Попробуем иначе:
- 5 + 2 = 7;
- 10 – 7 = 3.
Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:
25 – (18+2) = ?
Пробуем решить двумя способами:
- 25 – 18 + 2 = 9;
- 25 – 20 = 5.
Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:
- 18 + 2 = 20;
- 25 – 20 = 5.
Другого решения у ответа у примера быть не должно.
Итак:
ЧТО ВАЖНЕЕ – УМНОЖЕНИЕ ИЛИ СЛОЖЕНИЕ?
При решении примеров
Расставь порядок действий.
Умножить или разделить – на первом месте.
Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:
81 : 9 х 2 = ?
- 81 : 9 = 9;
- 9 х 2 = 18.

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?
Рассмотрим пример:
8 : 2 + 2 = ?
Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:
- 8 : 2 = 4;
- 4 + 2 = 6.
Значит, пример решен правильно. А если в нем будут скобки?
8 : (2 + 2) = ?
- 2 + 2 = 4;
- 8 : 4 = 2.
То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:
- Раскрываем скобки. Если их несколько, делаем вычисления для каждых.
- Умножение либо деление.
- Вычисляем конечный результат, выполняя действия слева направо.
Пример:
81 : 9 + (6 – 2) + 3 = ?
- 6 – 2 = 4;
- 81 : 9 = 9;
- 9 + 4 = 13;
- 13 + 3 = 16.

81 : 9 + (6 – 2) + 3 = 16.
А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.
Алгоритм решения выражения:
- Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.
- Выполняем вычисления в скобках.
- Делаем умножение и деление.
- Выполняем сложение и вычитание.
Пример:
28 : (11 – 4) + 18 – (25 – 8) = ?
Порядок вычисления:
- 11 – 4 = 7;
- 25 – 8 = 17;
- 28 : 7 = 4;
- 4 + 18 = 22;
- 22 – 17 = 5.
Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.
Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним.
МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С НУЛЕМ
Круглый нуль такой хорошенький,
Но не значит ничегошеньки.
В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:
5 × (8 : 2 – 4) = ?
- 8 : 2 = 4;
- 4 – 4 = 0;
- 5 × 0 = ?
При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:
0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;
Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:
0 : 5 = 0.
Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.
Напомним другие арифметические действия с нулем:
УМНОЖЕНИЕ И ДЕЛЕНИЕ НА ЕДИНИЦУ
Математические действия с единицей отличаются от действий с нулем. При умножении или делении числа на 1 получается само первоначальное число:
7 × 1 = 7;
7 : 1 = 7.
Конечно, если у вас есть 7 друзей, и каждый подарил вам по конфете, у вас будет 7 конфет, а если вы их съели в одиночестве, то есть поделились лишь с самим собой, то все они и оказались в вашем желудке.
ВЫЧИСЛЕНИЯ С ДРОБЯМИ, СТЕПЕНЯМИ И СЛОЖНЫМИ ФУНКЦИЯМИ
Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.
- Действия с дробями
Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:
25×38 = ?
- 2 × 3 = 6 — числитель
- 5 × 8 = 40 — знаменатель
Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:
28=25:35=?
28:35=28×53
- 2 × 5 = 10;
- 8 × 3 = 24.

28:35=1024=512
- Действия со степенями
Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:
(5² – 7) : 3 = ?
- 5² = 5 х 5 = 25;
- 25 – 7 = 18;
- 18 : 3 = 6.
(5² – 7) : 3 = 6.
Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.
- Действия с корнями, логарифмами, функциями
Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.
ГЛАВНЫЕ ПРАВИЛА ПО ТЕМЕ
Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:
2 + х = 5.
Аналогично:
8 : 2 = у × 2 = 8.
В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:
5 × 4 = 4 × 5.
При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.
Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста,
напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
Порядок действий в математике 3 класс: примеры. Что сначала
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.
Возведение степень — операция умножения числа на самого себя несколько раз.
Основание степени — число, которое повторяется сомножителем определённое количество раз. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Что сначала — умножение или сложение?
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
- 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
- 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
- 50 + 50 – это кучки малолетних работников;
- 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).
Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
- Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
- Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
- Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.

- После выполнения последнего действия ответ обязательно записывается в исходный пример.
Запомните! При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.
Запомните! Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Секрет безошибочного порядка действий
Всех людей, которые ловко решают примеры на смешанные действия, отличает одно свойство. Точнее даже — навык.
Они умеют «видеть» или воспринимать числа, стоящие по обе стороны от знака умножения или деления не как «отдельно стоящие циферки», а как «единое число» (выраженное в такой странной форме).
Говоря наглядно, в нашем примере:
2 + 6 — 8 : 2
человек «видит» не четыре числа, а только три:
- Двойка
- Шестерка и
- 8:2, которые воспринимает как единое число.
Как правило, это неосознанное, невербализованное восприятие. Мозг мгновенно производит эту операцию, и человек не замечает её.
Этот навык вырабатывается долгим «нарешиванием» огромного количества длинных примеров. К старшей школе уже у многих детей есть.
К старшей школе уже у многих детей есть.
Но можно попробовать ускорить события.
Предложу вам упражнение для отработки такого «видения».
Примеры на порядок действий 3-4 класс для тренировки
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.
 А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
Определи порядок действий в данных выражениях. Найди значение выражений.
***
Определи, в каком выражении такой порядок выполнения действий:
- умножение;
- деление;.
- сложение;
- вычитание;
- сложение.

Найди значение данного выражения.
***
Составь три выражения, в которых такой порядок выполнения действий:
- умножение; 2. сложение; 3. вычитание
- сложение; 2. вычитание; 3. сложение
- умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150
Расставь порядок действий. Найди значение выражения:
- (12 – 0 : 4) : 3 – (7 — 7)*45 + (36 : 6) : (15 : 15)
- 36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
- (3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
- (630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
- 5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
- 8040 : 6 + (109004 – 76048) : 7
- (64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
- 240400 – (5796 + 1803200 : 400) * 8
- 345 * (250 * 125) * (8 * 400)
- 56432 : 8 * 50 – (223956 + 882630 : 9)
- (62456715 + 548185) : 700 – 300 * 80450 : 5000
- 80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
- (1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
- (600000 – 538704) * 500 : 300
- 280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
- (250 * 840 – 145 * 1008) : 60
- (1000 – 832) * 715 : 30 + (104402 – 58842 : 7)
Дополнительные примеры
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Материалы по теме Адаптация ребенка 3–4 лет к детскому саду
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Вычисляем:
10 + 15 = 25
25 – 6 = 19
19 – 8 = 11
Полностью пример записываем так:
10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Вычисляем:
15 : 5 = 3
3 • 4 = 12
12 : 6 = 2
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
15 : 3 = 5
6 • 8 = 48
10 – 5 = 5
5 + 48 = 53
Полностью пример записываем так:
10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53
Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
25 – 10 = 15
15 : 3 = 5
6 • 8 = 48
5 + 48 = 53
Полностью пример записываем так:
(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
12 : 4 = 3
6 + 3 = 9
18 : 9 = 2
42 + 2 = 44
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Сложение, вычитание, умножение и деление: правила
Может быть полезно понять, как использовать различных математических операции , поскольку их можно использовать каждый день во многих различных ситуациях, точно так же, как вычисление того, как можно разделить поровну пакет со сладостями. между группой людей.
Определение сложения, вычитания, умножения и деления
Сложение, вычитание, умножение и деление — все типы операций, используемых в математике.
Сложение
Сложение — это тип операции, результатом которой является сумма двух или более чисел. Существует знак для обозначения операции сложения, называемый знаком плюс, который представляет собой .
Вычитание
Вычитание — это тип операции, результатом которой является нахождение разницы между двумя числами. Знак, обозначающий операцию вычитания, называется знаком минус и выглядит следующим образом.
Умножение
Умножение — это операция, требующая сложения равными группами, в результате умножения получается произведение. Знак, обозначающий операцию умножения, можно назвать знаком умножения и выглядит он так.
Деление
Деление — операция, обратная умножению, заключается в разбиении числа на равные части. Знак, представляющий операцию деления, называется просто знаком деления и выглядит так.
Правила сложения, вычитания, умножения и деления
Существуют различные правила и методы, которые могут быть полезны при использовании каждой из этих операций.
Сложение
При сложении двух или более чисел можно использовать метод сложения столбцов. Это включает в себя размещение чисел одно над другим в столбце, затем вы работаете справа налево, добавляя числа, которые находятся в одном столбце.
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальных числа вместе, начиная с 2 и 2:
Теперь перейдем к 2 и 5:
И, наконец, 5 и 1:
Следовательно,
Если два добавляемых вами числа больше 10, вы можете перенести это число.
Вычитание
При вычитании двух чисел можно также использовать метод столбца; метод вычитания столбцов. Это работает так же, как метод сложения столбцов, однако вы вычитаете числа, а не добавляете их.
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, от которого вы вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 8 и 4:
Теперь переходим к 3 и 1:
И, наконец, 5 и 2:
Следовательно,
Если вычитаемое число больше, чем вычитаемое, вам нужно взять цифру. из столбца влево.
из столбца влево.
Умножение
При умножении двух чисел можно использовать различные методы, включая метод сетки. Это включает в себя разбиение двух чисел и размещение их в сетке. Затем вы выполняете отдельные умножения, а затем складываете их все вместе.
Рассчитайте
Решение:
Для начала, вытяните сетку, разбивайте свои числа и поместите их в сетку, похожую на сетку:
| 20 | 3 | |
| 3 | ||
| 3 | ||
| 9000 3 | 3||
| 2 |
, чтобы заполнить сетку.0107
Следовательно,
Деление
При делении одного числа на другое вы можете использовать метод, называемый коротким делением, этот метод лучше всего работает, когда вы делите число на 10. или менее. Короткое деление предполагает мысленное деление числа на более мелкие этапы.
или менее. Короткое деление предполагает мысленное деление числа на более мелкие этапы.
Вычислить
Решение:
Для начала вы можете нарисовать свой расчет, записав число, на которое вы делите, слева, а число, которое вы делите, запишите справа, как показано ниже:
Теперь вам нужно проработать число, которое вы делите по одной единице за раз, начните с выяснения, сколько раз 9 может перейти в 3. Поскольку это невозможно, вам нужно перенести 3 на следующую единицу. :
Теперь вы можете подумать о том, сколько раз 9 может перейти в 30. 9 входит в 30 три раза с остатком три:
Затем это можно записать в ваше деление, как показано ниже, с делимым числом, записанным над вычислением. а остаток 3 переносится на 6:
Наконец, вы можете подсчитать, сколько раз 9 входит в число 36:
Следовательно,
Сложение, вычитание, умножение и деление отношений
Операции могут иметь отношения друг с другом. Существует связь между сложением и вычитанием, а также связь между умножением и делением.
Существует связь между сложением и вычитанием, а также связь между умножением и делением.
Сложение и вычитание
Сложение и вычитание можно считать обратными друг другу. Это просто означает, что операции противоположны, вы можете отменить сложение, вычитая то же число, и наоборот!
Умножение и деление
Умножение и деление также считаются обратными друг другу, если вы хотите отменить умножение, вы можете просто разделить число.
Примеры сложения, вычитания, умножения и деления
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальные числа вместе. Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:
Теперь вам нужно сложить вместе 4, 7 и 1, опять же, поскольку это больше 10, вам нужно перенести единицу:
Наконец, вы можете сложить вместе 6, 2 и 1:
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, из которого вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 2 и 6. Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:
Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:
Теперь из 2 можно вычесть 2:
Наконец, из 7 можно вычесть 4:
Рассчитать
your numbers, and place them into the grid-like so:
| 50 | 3 | |
| 30 | ||
| 5 |
To fill out the grid you simply multiply each number in the columns:
| 50 | 3 | |
| 30 | 1500 | 90 |
| 5 | 250 | 15 |
Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:
Вычислить
Решение:
Давайте начнем с записи суммы, используя метод короткого деления:
Теперь начнем с вычисления, сколько раз 7 входит в 4, это невозможно, так что вы можете перенести 4 на 3:
Затем вы можете посмотреть, сколько раз 7 может войти в число 43:
Это оставляет нам остаток от 1, который можно перенести на 4:
Наконец, посчитайте, как много раз 7 может перейти в 14:
Следовательно,
Применения сложения, вычитания, умножения и деления
Эти операции часто используются в повседневной жизни, давайте рассмотрим несколько примеров:
В коллекции Эми 326 наклеек, у Клэр 213 наклейки. Сколько наклеек у них было бы, если бы они объединили свои коллекции?
Сколько наклеек у них было бы, если бы они объединили свои коллекции?
Решение:
Начните с размещения двух чисел друг над другом:
Теперь вы можете складывать их вместе, работая справа налево, начиная с 6 и 3:
Работайте по номерам:
Следовательно, если Эми и Клэр объединит свои коллекции, у них будет 539 наклейки в коллекцию.
У Сэма 142 конфеты, он отдает своему другу 54, сколько конфет осталось у Сэма?
Решение:
Чтобы узнать, сколько конфет у Сэма, мы можем вычесть 54 из 142. Для начала поместите два числа друг над другом:
Теперь, работая справа налево, вычтите одно число из другого. Не забывайте, так как 2 меньше 4, вам нужно взять единицу из столбца слева:
Теперь вы можете двигаться дальше, опять же, поскольку 3 меньше 5, вам нужно будет взять единицу из столбца слева. столбец слева:
Следовательно, у Сэма осталось 88 конфет .
Дейв готовит на 12 человек, но по его рецепту он рассчитан только на 4. Если по рецепту требуется 72 грамма пасты, сколько пасты понадобится Дейву?
Решение:
Чтобы узнать, сколько пасты понадобится Дейву для его рецепта, мы можем использовать операцию умножения. Поскольку 4 входит в 12, 3 раза, Дейву понадобится в три раза больше, чем указано в рецепте. Для этого мы можем использовать метод сетки:
| 70 | 2 | |
| 3 | 210 | 6 |
Теперь. Теперь. , Дейву понадобится 216 грамм пасты на 12 персон.
Барбара обедает с тремя друзьями, счет составляет 188 фунтов стерлингов, и они решают разделить его поровну. Сколько платит каждый человек?
Решение:
Для начала запишите задачу, используя метод короткого деления. Счет составил 188 фунтов стерлингов, и его делят между 4 людьми, поэтому его можно записать следующим образом:
Теперь сделайте первый шаг и посмотрите, сколько раз 4 может войти в первое число слева. Поскольку 4 не может перейти в 1, 1 можно перенести:
Поскольку 4 не может перейти в 1, 1 можно перенести:
Теперь подсчитайте, сколько раз 4 может входить в число 18:
Остается 2:
Наконец, сколько раз 4 может входить в число 28:
означает, что каждому человеку нужно будет заплатить
£47 .Сложение, вычитание, умножение и деление – основные выводы
- Существует множество различных типов математических операций, в том числе:
- Сложение – операция, результатом которой является сумма двух или более чисел.
- Вычитание — операция, результатом которой является нахождение разницы между двумя числами.
- Умножение, которое представляет собой операцию, требующую сложения в равных группах, в результате умножения получается произведение.
- Деление — операция, обратная умножению, включает в себя разбиение числа на равные части.
Что такое порядок действий? — Определение, правила и примеры
Порядок действий – это набор правил, которым необходимо следовать в определенном порядке при решении уравнения.
Все мы хорошо знаем четыре основных математических действия: сложение, умножение, деление и вычитание. С детства мы постоянно репетируем задачи, связанные с этими четырьмя операциями. Эти операции используются, от добавления счета за вашу покупку в торговом центре до разделения пиццы на четыре равные части. Но до сих пор мы решали проблемы, связанные с каждой операцией в отдельности. Что, если у нас есть выражение, в котором все четыре операции работают вместе? Мы сначала умножаем или сначала вычитаем? Это может быть проблематично, если вы будете следовать неправильному подходу. Это может привести к неправильным ответам. Поэтому порядок действий вступил в силу.
Анализ любого математического утверждения с использованием арифметических операций, таких как деление, умножение, сложение и вычитание, в математике называется операциями. Давайте посмотрим на законы порядка операций и посмотрим, насколько хорошо мы можем их вспомнить, используя простые стратегии. В этой статье вы узнаете порядок операций, правила порядка операций, математический порядок операций и решите задачи на порядок операций.
Почему выполняется Порядок операций?
При вычислении уравнений в арифметике может потребоваться выполнение множества операций, и упрощение, в конце концов, дает разные результаты. Однако на каждую фразу может быть только один правильный ответ. Мы используем принципы, чтобы упростить любое данное математическое выражение, чтобы найти правильный ответ. Эти принципы основаны на всех основных математических операторах.
С единственной целью всегда получать правильные ответы на любое математическое уравнение, был реализован порядок операций.
Каков порядок действий?
В математике такие операторы, как сложение (+), вычитание (-), умножение (×) и деление (÷), имеют приоритет друг над другом. Мы не можем самостоятельно решить выражение, содержащее любой из двух операторов. Мы должны следовать правилам порядка операций, которые гласят, что в любом выражении, как арифметическом, так и алгебраическом, первыми будут оцениваться скобки. Заказ будет рассчитываться во вторую очередь. Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.
Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.
The priority of solving any expression is mentioned in the table below:
| Priority | Operation |
| First | Brackets (), {}, [ ] |
| Second | Порядки (Экспоненты, Квадратный корень, Кубический корень, Логарифмический и т. д.) |
| Третьи | Деление или умножение (Операция, расположенная слева от выражения, будет оцениваться первой) |
| Четвертая | Сложение или вычитание (в зависимости от того, какая операция находится в левой части выражения, будет оцениваться первой) |
Определение порядка операций принципы приоритета, которые мы используем при решении любого математического уравнения, включающего множество операций.
 Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.
Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.Давайте теперь разберемся с порядком операций, правило за правилом, в соответствии с установленным приоритетом: операторы, применяемые к выражению. При решении любого выражения всегда двигайтесь от левой стороны к правой. Это поможет вам облегчить упрощение этого выражения. Теперь прочитайте правила, упомянутые ниже, чтобы полностью понять концепцию порядка операций:
Правило 1: Необходимо всегда проверять наличие скобок или круглых скобок в выражении. Чаще всего в математических выражениях встречаются скобки «()», «{}» и «[]». Если терм содержит все три квадратных скобки, решите уравнение следующим образом:
- Сначала решите термины внутри круглой скобки «()» или круглых скобок.
- Решите условия внутри фигурных скобок ‘{}’ секунда.
- Наконец, решите условия в квадратных скобках «[ ]».

Кроме того, помните, что если в любой из скобок есть несколько операций, обязательно используйте порядок операций для их решения.
Правило 2: После того, как вы решите числа в скобках, найдите любые термины в следующем порядке, такие как возведенные в степень термины, корневые термины, логарифмические термины, тригонометрические термины и т. д., и решите их.
Правило 3: Осталось расставить четыре основных оператора в правильном порядке. Вы можете выполнять умножение или деление в зависимости от того, какой оператор стоит первым с левой стороны выражения.
Правило 4: Последним шагом является добавление или вычитание элементов в том же порядке слева направо.
Если вы помните эти пять правил, значит, вы усвоили порядок действий. Каким бы длинным ни было выражение, вы легко сможете решить его, не задумываясь. Если вы не уверены, что запомните эти правила, есть два простых способа их запомнить. Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.
Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.
Способы запоминания порядка операций – BODMAS и PEMDAS
Существует два очень важных способа запоминания порядка операций. Они сокращенно называются правилом PEMDAS и правилом BODMAS. Буквы в этих аббревиатурах определяют математические операции. Буква, которая присутствует первой, применяется первой к любому уравнению.
Давайте теперь узнаем, что означает каждая из букв в этих аббревиатурах:
Порядок операций BODMAS
BODMAS — наиболее распространенная аббревиатура для порядка операций. Многие из вас наверняка слышали об этом где-то в своей жизни. В развернутом виде это означает:
- B — Кроншеты (), {}, []
- O — Порядок
- D — Дивизион (÷)
- 9 M (÷)
- 9 M —Lipe (÷)
- 9 MALICKAT
- A – Сложение (+)
- S – Вычитание (-)
Порядок операций PEMDAS
Операция PEMDAS для порядка акронимов. Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.
Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.
- P – Скобки (), {}, [].
- E — ЭКСПОНЕР (A2) (например, здесь, A — это число с показателем 2 )
- M — Умножение (×)
- D –. )
- A – означает сложение (+)
- S – означает вычитание (-)
Это наиболее эффективный метод запоминания последовательности событий. Забавная фраза « Пожалуйста, извините, моя дорогая тетя Салли »- хороший способ запомнить PEMDAS.
Оба эти метода используются для упрощения нашего понимания порядка операций. Мы увидим пример порядка операций, чтобы прояснить эту тему.
Каков порядок операций в математике?
Порядок операций — это правило, определяющее правильную последовательность шагов для вычисления математического выражения. Если у вас есть выражение только с одной операцией (например, только сложение, только вычитание, только умножение или только деление), правильный способ его решения — слева направо. Однако для выражений с несколькими операциями необходимо соблюдать порядок операций.
Если у вас есть выражение только с одной операцией (например, только сложение, только вычитание, только умножение или только деление), правильный способ его решения — слева направо. Однако для выражений с несколькими операциями необходимо соблюдать порядок операций.
Как вы используете порядок операций?
Пример порядка операций
Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.
- Для вычисления арифметических операций
Выражение 1: 2 + 3 x 5 к результату. 15 + 2 = 17,
Выражение 2: 15 ÷ 3 x 2 – 6
- Правильный способ: Правильный способ решить это выражение – сначала разделить 15 и 3 = 5, потому что оно ближе к левой части выражения.
 Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4.
Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4. - Неправильный способ: Если умножить 3 x 2 = 6, то вычесть из него 6, мы получим 15 ÷ 0 = не определено . Это неправильный способ решения этого выражения.
- Правильный способ:
Выражение 1: 6 x 32
- Правильный способ: Теперь правильный способ решить это выражение = 9, то есть 3, то есть 3, сначала решить порядок 2, порядок. умножьте это на 6. 9 x 6 = 54.
- Неправильный способ: Если умножить 6 x 3 = 18, то возведите ответ в квадрат, мы получим, 182 = 324, что неверно.
Выражение 2: 2 x sin 30
- Правильный способ: Сначала оцените порядок sin 30 = ½. Теперь умножаем 2 на ответ. 2 x ½ = 1
- Неправильный способ: Если умножить 30 на 2 = 60 и решить порядок, то получим sin 60 = 3/2.
 Что является неправильным ответом
Что является неправильным ответом
- Для вычисления скобок
Выражение 1: (12 + 3) x 4
Решение: В этом выражении мы видим, что скобки; следовательно, мы сначала решим содержимое в скобках. Следовательно, 12 + 3 = 15. Теперь умножаем 15 на 4 = 60.
Выражение 2: 4 – 32 ÷ 8
4 – 32 ÷ 8 = 8 – 8 = 0 – это решение. (Это правильно. Это правильный способ.)
Рассмотрим другой подход к тому же выражению.
4 – 32 ÷ 8 = (-28) ÷ 8 = -3,5 (Неверно (это неверный метод)
Выражение 3: 8 x (6 + 6)
8 x (12) = 96 (Это правильный способ решения скобок.)
Рассмотрим другой метод для того же выражения.
8 x (6 + 6) = 48 + 6 = 54 (Это неправильный способ решения скобок.)
Примечание: Мы должны соблюдать шаблон операторов при выполнении порядка операций на любом данная фраза.





 А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.


 Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4.
Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4. 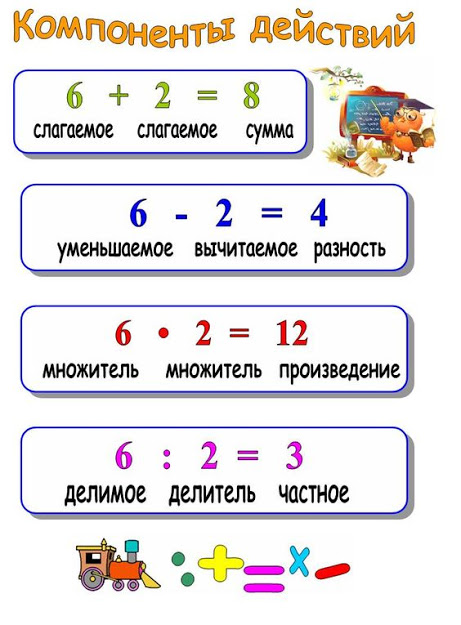 Что является неправильным ответом
Что является неправильным ответом