Тренажер по устному счету в пределах 20. Сложение и вычитание с переходом через десяток. 1 класс (Ольга Федоскина)
65 ₽
+ до 9 баллов
Бонусная программа
Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.
Купить
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Осталось мало
Нет в наличии в магазинах сети
25
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Тетрадь-тренажёр разработана для тренировки навыков устного счёта сложения и вы-1 читания в пределах 20 с переходом через десяток.
Тренажёр включает 3 темы. Для удобства учеников в теиах 1 и 2 предложены отдельно задания на сложение и отдельно на вычитание. Тема 3 включает задания для закрепления и повторения таблиц сложения и вычитания в пределах 20 с переходом через разряд десятка в заданиях смешанного типа.
Тема 3 включает задания для закрепления и повторения таблиц сложения и вычитания в пределах 20 с переходом через разряд десятка в заданиях смешанного типа.
В середине тетради размещены контрольные страницы к каждой предложенной теме и итоговый тест. Эти страницы рекомендуем заранее удалить и использовать по усмотрению. После выполнения каждой работы ученик может проверить результаты по ответам.
Для удобства организации этапа самоконтроля ребёнка в тетради есть специальная страница ответов, которую также советуем отрезать и использовать после выполнения задания.
Пособие позволит родителям и педагогам определить степень освоения материала ребёнком, выявить пробелы и организовать работу по их устранению.
Издание подходит для занятий по разным учебным программам школ и адресовано ученикам 1 и 2 классов, их родителям, педагогам.

Описание
Характеристики
Тетрадь-тренажёр разработана для тренировки навыков устного счёта сложения и вы-1 читания в пределах 20 с переходом через десяток.
Тренажёр включает 3 темы. Для удобства учеников в теиах 1 и 2 предложены отдельно задания на сложение и отдельно на вычитание. Тема 3 включает задания для закрепления и повторения таблиц сложения и вычитания в пределах 20 с переходом через разряд десятка в заданиях смешанного типа.
Многие задания включают игровой компонент, подсказки для самопроверки. К некоторым заданиям даны ответы на специальных страницах. Каждая тема завершается заданием на скорость счёта, которое выполняется с секундомером и позволяет проверить результаты.
В середине тетради размещены контрольные страницы к каждой предложенной теме и итоговый тест. Эти страницы рекомендуем заранее удалить и использовать по усмотрению. После выполнения каждой работы ученик может проверить результаты по ответам.

Пособие позволит родителям и педагогам определить степень освоения материала ребёнком, выявить пробелы и организовать работу по их устранению.
Издание подходит для занятий по разным учебным программам школ и адресовано ученикам 1 и 2 классов, их родителям, педагогам.
Принтбук
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Книга «Тренажер по устному счету в пределах 20. Сложение и вычитание с переходом через десяток. 1 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Ольга Федоскина
«Тренажер по устному счету в пределах 20. Сложение и вычитание с переходом через десяток. 1 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Примеры до 20 первый класс: Примеры математика 1 класс в пределах 20: сложение, вычитание, тренажер (распечатать)
Содержание
Примеры математика 1 класс в пределах 20: сложение, вычитание, тренажер (распечатать) | карточки
В 7 лет ребенок 1 класса должен уметь решать примеры в пределах 20 на сложение и вычитание. Математика 1 класс обучает детей:
- называть числа в прямом и обратном порядке,
- решать задачи и примеры в одно действие на сложение и вычитание;
- измерять длину линейкой;
- пользоваться арифметическими знаками — больше, меньше, равно;
- определять время на часах.
Дети 1 класса должны очень хорошо усвоить данную программу и тренажеры, чтобы потом двигаться дальше. Поэтому мы подготовили для вас много примеров по математике на сложение и вычитание для 1 класса.
Примеры по математике на сложение с переходом через разряд в пределах 20 (для 1 класса)
Предлагаем ребенку 1 класса решить примеры до 20 на сложение. Чтобы видеть результат и прогресс ребенка, записывайте, сколько ошибок сделал первоклассник и время, затраченное на примеры.
Чтобы видеть результат и прогресс ребенка, записывайте, сколько ошибок сделал первоклассник и время, затраченное на примеры.
Математика 1 класс: Реши примеры на сложение в пределах 20 (карточки)
Чтобы улучшить навыки счета у детей 1 класса, нужно выполнять примеры тренажеры каждый день по 15-20 минут в день. Так ребенок 1 класса быстро усвоит программу.
Карточки тренажеры по математике 1 класс на сложение в пределах 20
Еще один вариант карточек тренажеров счета до 20 для 1 класса. Обязательно сравнивайте результат ребенка по прошествии времени, вы увидите прогресс и рост — скоро ребенок будет без труда решать примеры в уме.
Распечатать примеры 1 класс по математике до 20 (с переходом через разряд)
Карточки: Реши примеры в пределах 20 (для 1 класса)
Примеры математика сложение и вычитание в пределах 20
Примеры математика сложение и вычитание в пределах 20
Примеры математика сложение и вычитание в пределах 20: карточки
Математические примеры и тренажеры в пределах 20: сложение и вычитание
Примеры по математике до 20 на сложение: тренажеры 1 класс
Примеры по математике до 20 на вычитание
МАТЕМАТИЧЕСКИЙ ТРЕНАЖЕР ДЛЯ ПЕРВОКЛАССНИКОВ В КЛЕТОЧКУ
Математические примеры-кроссворды для 1 класса (примеры до 10)
Реши примеры в пределах 20 и раскрась (математические раскраски)
Очень интересное задание для 1 класса. Дети очень любят разукрашивать.
Дети очень любят разукрашивать.
Математические примеры и задачи для школьников 1 класса
Веселые гусеницы-примеры до 20
Математические примеры-раскраски для мальчиков и девочек
Окно в Мир
| |||
Что должны знать все учителя
Математические советы и стратегии для развития чувства числа до 20 в детском саду и первом классе: Включен обширный список заданий и ресурсов для изучения числа: книги, материалы, математические манипуляции и БЕСПЛАТНЫЕ занятия!
Математические советы и стратегии, необходимые для развития чувства числа до 20, находятся прямо здесь. У вас будет все, что вам нужно, чтобы быстро внедрить множество заданий, игр и центров, связанных с числами, в свой класс или домой.
У вас будет все, что вам нужно, чтобы быстро внедрить множество заданий, игр и центров, связанных с числами, в свой класс или домой.
Building Number Sense до 20
Занятия, книги, предложения ресурсов (включая БЕСПЛАТНУЮ) охватывают множество концепций числового смысла и идеально подходят для детского сада и первого класса. Кроме того, вы найдете ценные материалы по численному смыслу и манипулятивные предложения, а также бесплатные подарки, которые вы можете получить уже сегодня! Предупреждение: он ДЛИННЫЙ, но в нем так много всего, что вы не захотите ничего пропустить!
Почему важен смысл номера здания?
Детям нужны возможности изучать числа и знакомиться с ними. Научиться считать, определять числа и понимать количество — это лишь некоторые из основных понятий. Повторяющийся опыт способствует пониманию и свободному обращению с числами. Этот опыт помогает расширить знания и узнать новые идеи. Сильное чувство числа жизненно важно для будущего понимания более сложных математических тем.
Приведенные ниже действия успешно использовались. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Быть гибким. Обсуждайте числа и поощряйте вопросы. Когда есть возможность заказать, посчитать, сопоставить или описать вместе с ребенком, дерзайте! Им выгодно видеть числа естественным и плавным образом.
Каждый день уделяйте время веселым и увлекательным занятиям с числами и наблюдайте за развитием беглости речи.
Концепции и действия по распознаванию чисел
Чувство числа сборки через счет
Очень важно считать с детьми каждый день. Повторяющийся устный счет помогает им услышать, как звучат числа, и запомнить их порядок. Использование математических манипуляций, таких как подсчет фишек, может помочь установить связь с вербальным счетом и счетом объектов. Этот счет один к одному является важным навыком, который необходимо часто практиковать.
Занятия
- Считайте вслух всем классом, начиная с единицы и постепенно увеличивая число.

- Сядьте с партнером или в круг и по очереди считайте по 1.
- По мере того, как счет будет развиваться, учите модели чисел и счет 2, 5 и 10.
- Используйте числовую диаграмму, чтобы посмотреть, как числа выглядят визуально. Укажите на каждое число, как оно сказано.
- Поощряйте детей практиковать прямой счет с маленькими предметами. Поставьте небольшие группы предметов в центре, чтобы их можно было сосчитать.
- Раздайте детям карточки с числами (подобные тем, что показаны ниже), чтобы они могли изображать их с помощью счетных фишек.
Развивайте чувство числа, сопоставляя числа с количествами
Предоставьте детям материалы для счета и связи с предметами и числами. Это побуждает детей видеть, что цифры — это больше, чем слова. Объясните детям, что у чисел есть много представлений, таких как точки, пальцы, счетчики, цифры, предметы, десять рамок и т. д.
Занятия
- Сопоставьте два разных типа объектов вместе, например, пять считающих медведей и домино, которое показывает пять точки.

- Используйте ссылки, чтобы создать числовую цепочку для номера.
- Доработайте до показа количества с более чем двумя типами объектов (как видно на фото).
- Имейте множество различных предметов для занятий, таких как игральные кости, домино, магниты с числами, медведи, счетные фишки, кубики и числовые карты.
- Сопоставьте числовые карты из карточной колоды или игры Уно с точками на домино. Найдите все комбинации чисел на костяшках домино.
- Соберите головоломки с числами, каждая из которых имеет свое числовое представление. Они помогают детям увидеть, что числа можно моделировать разными способами. Эти числовые головоломки до 20 доступны для БЕСПЛАТНОЙ загрузки далее.
- Поощряйте счет один к одному с помощью карточек с вырезками. Дети считают группы предметов и вырезают цифру, которая соответствует нужному количеству.
- Десять рамок отлично подходят для систематизации чисел, чтобы их можно было легко сосчитать.
 Сопоставление числовых карточек с десятью изображениями рамок является простым, но эффективным способом связи количества с числами.
Сопоставление числовых карточек с десятью изображениями рамок является простым, но эффективным способом связи количества с числами.
Развивайте чувство числа с числом дня
Когда дети видят числа разными способами одновременно и многократно, их чувство числа развивается. Выберите число дня, начинающееся с единицы, и проанализируйте его во время математического блока.
Занятия
- Узнайте о конкретном номере за каждый день, проведенный в школе. Научите и проанализируйте это число в течение календарного времени. Представьте это число на числовой прямой, сосчитайте до этого числа, покажите это число с помощью соломинок или кубиков и т. д.
- Используйте плакат с номером дня или якорную диаграмму, чтобы разбить числа. Создайте свой плакат с номером дня с помощью БЕСПЛАТНЫХ шаблонов плакатов.
- Поощряйте детей к участию и демонстрируйте свое понимание на бумаге или мини-досках. Задайте вопрос, например: «Как мы покажем 5 с подсчетом баллов?» и дайте им время попробовать самостоятельно.
 Это отличная разминка для развития беглости перед уроками математики.
Это отличная разминка для развития беглости перед уроками математики. - Прочтите дополнительные советы о том, как начать распорядок дня в классе.
Распознавание чисел путем заказа номеров
Предоставьте детям возможность упорядочивать числа. Располагая числа или объекты с числами в правильном порядке, они считают и развивают чувство числа.
Занятия
- Предоставьте возможности с помощью числовой линии и числовой диаграммы, которые упорядочивают числа для нас.
- Расставьте наборы чисел в правильном порядке, найдя их на числовой прямой.
- Заклейте разные числа на таблице с числами стикерами и попросите детей назвать недостающие числа.
- Собирайте наборы Lego, собирая детали в порядке, указанном на блоках.
- Вместе с партнером закажите карточки с числами от 0 до 20. Создайте гусеницу с числами, как показано ниже.
- Головоломки с числами — это интересный способ упорядочить числа.
 Поместите полоски в правильном порядке, чтобы открыть изображение.
Поместите полоски в правильном порядке, чтобы открыть изображение.
- Пазлы легко и просто создавать. Возьмите старую головоломку и напишите числа на обратной стороне каждой части.
- Возьмите лист бумаги и напишите числа в ряд. Вырежьте произвольно кусочки и торгуйте с партнером. Снова соберите пазл для практики.
- Пройдите лабиринт с порядковым номером, начиная с 0. Это задание можно использовать повторно, если положить его в карманный протектор.
Смысл номера сборки с действиями по разрядному значению
Обучение детей порядковому значению должно начинаться с обучения их видеть десять разными способами. Перейдите к иллюстрированию чисел с помощью десятичных блоков.
Занятия
- Потренируйтесь составлять группы из десяти предметов. Сгруппируйте соломинки, бобы, прилавки или любые мелкие предметы.
- Обучайте счет десятками для групп. Сначала перейдите к обучению групп, а затем одиночных занятий.

- Объединитесь в группы по десять человек, чтобы добраться до 100-го дня.
- Показать и изучить блок десятков и блок единиц. Обсудите, что в блоке десятков сложено десять единиц.
- Используйте блоки десятичной системы счисления для представления чисел. Сделайте много примеров, где дети должны использовать и считать кубики. Используйте диаграмму, чтобы помочь сосчитать блоки.
- Скажите: «Покажи (или нарисуй) мне 14 кубиков разряда!»
- Представляет количество десятков и единиц на матах с разрядным значением (см. ниже). Задавайте вопросы типа «Сколько их?» или «Сколько групп по десять человек?». Убедитесь, что они понимают, что означает каждое число в числе (например, 1 из 18 — это десятка, а не единица).
- Представление числа различными способами: расширенная форма, стандартная форма, словоформа, цифра и т. д. Рабочие листы, подобные приведенному ниже, могут помочь установить эту связь.
Чтение и запись цифр
Дети постоянно окружены числами в своем окружении. Они быстро учатся распознавать отдельные цифры от 0 до 9 с помощью различного опыта. Продолжайте поощрять это знакомство, размещая цифры на стене. Плакаты, числовые строки и календари являются полезными инструментами.
Они быстро учатся распознавать отдельные цифры от 0 до 9 с помощью различного опыта. Продолжайте поощрять это знакомство, размещая цифры на стене. Плакаты, числовые строки и календари являются полезными инструментами.
Занятия
- Собери числа из пластилина в математическом центре. Даже такая простая вещь, как это пластилин, показывает активность.
- Ежедневно печатайте числа от 0 до 9 разными способами – в буклетах, на досках во время уроков математики и т. д.
- Нарисуйте числа на бумаге и дайте учащимся расставить точки маркерами или бинго-дабберами, чтобы расставить точки.
- Используйте доску Boogie Board (см. ниже) или белую доску, чтобы быстро практиковать числа снова и снова.
- Часто повторяйте числа, чтобы построить координацию и правильную форму. Мини-книга ниже поощряет это, а также номера местонахождения.
- Поощряйте правильное формирование чисел, обучая этому явным образом.
Плакаты (см.  ниже) являются полезными инструментами для использования и размещения на стене.
ниже) являются полезными инструментами для использования и размещения на стене. - Запоминающиеся стихотворения о числах помогают учащимся визуализировать и запомнить формирование чисел. Используйте все свое тело, чтобы совершать действия или рисовать в воздухе.
Чтение и запись числовых слов
Научите детей читать числовые слова, пока они учатся читать. Учите каждое числовое слово по одному и произносите их фонетически (если применимо).
Мероприятия
- Имейте плакаты с номерами, на которых есть и цифра, и числовое слово.
- Включите числовые слова в списки правописания, чтобы дети научились читать и писать числовые слова.
- Используйте номер распорядка дня, чтобы учить и сосредотачиваться на одном слове каждый день.
- Сопоставьте карточки со словами с числами и карточками с числами (см. ниже).
- Играйте в память с партнером со словами-цифрами и карточками с числами. Ищите пары (двенадцать и 12).
- Развивайте распознавание и скорость с помощью флеш-карточек для ментальной арифметики.
 Карточки для детей, и они соревнуются, чтобы назвать то, что они видят (счет, цифры, числовые слова и т. д.).
Карточки для детей, и они соревнуются, чтобы назвать то, что они видят (счет, цифры, числовые слова и т. д.).
Развивайте чувство числа, считая вперед и назад
Научите детей считать от числа вперед и назад, чтобы подготовить детей к сложению и вычитанию.
Упражнения
- Дайте учащимся число и группу мелких предметов, которые они будут считать. Спросите: «Сколько у меня еще есть?» дается 7 для начала и группа из 9 жетонов, на которые можно рассчитывать.
- Играйте в игры с мелкими предметами и колодами карт, где необходим расчет.
- Сыграйте в групповую счетную игру под названием «Вокруг света». Произнесите число, и каждый человек будет считать и называть следующее число, пока вы идете по кругу.
- Используйте маленькие предметы, чтобы считать в прямом или обратном направлении от заданного числа (кубики, жетоны, игральные кости и т. д.).
- Расположите числа в обратном порядке. Возьмите описанные выше действия по упорядочиванию и измените их.

Build Number Sense by Estimating
Предоставьте детям множество возможностей угадать, сколько вещей они видят в своей повседневной жизни. Задавайте наводящие вопросы, чтобы стимулировать это мышление. Убедитесь, что дети знают, что они оценивают и что это всего лишь догадки. Подчеркните, что оценки не обязательно должны быть точными, но они должны быть продуманными. С большей практикой оценки должны стать ближе к фактическому количеству объектов.
Занятия
- Наполните прозрачные или открытые контейнеры предметами разного размера, чтобы дети могли их угадать. Держите их простыми и работайте над сложностью и размером объектов. Меньшие объекты и большие контейнеры обычно сложнее.
- Создайте оценочную станцию», где устанавливаются контейнеры с объектами внутри. Дети могут внимательно посмотреть и сделать оценки.
- В качестве группового занятия возьмите кучу предметов, чтобы быстро их показать. Накройте их и пусть дети делают предположения.

- Игра «Покажи и спрячь» с партнером. Используйте чашку и поместите внутрь несколько маленьких счетных мишек. Быстро покажите партнера, а затем спрячьте его. Они делают оценку, а затем вы вместе считаете, чтобы проверить.
Развивайте чувство числа путем сравнения чисел
По мере того, как растет знакомство с числами, растет и способность сравнивать числа друг с другом. Обеспечьте возможность сравнивать числа ежедневно. Задавайте вопросы о том, какое число больше, меньше или одинаково.
Действия
- Используйте диаграмму или числовую линейку для сравнения чисел.
- Используйте маленькие предметы, чтобы упростить сравнение. Скажите «Покажи 11 и 15 кубиками». Спросите: «Какое число меньше?».
- Научите символы и = и их значение. Используйте стратегию аллигатора (Аллигатор любит есть побольше), чтобы запомнить знаки и их значение.
- Создание числовых башен. Дети используют кубики для формирования башен для представления чисел.
 Сравните две башни, чтобы увидеть, какая из них самая высокая и, следовательно, большее число. Аллигатор съедает большую башню.
Сравните две башни, чтобы увидеть, какая из них самая высокая и, следовательно, большее число. Аллигатор съедает большую башню. - Сравните числа с помощью математических инструментов и укажите правильный символ на карточках с картинками (см. ниже). Когда дети станут свободно говорить, они должны распознавать правильный символ без посторонней помощи.
Действия, описанные в этом посте, можно найти в следующих ресурсах, которые можно найти на сайте «Учителя платят учителям».
Числа до 5 для детского сада
Числа до 10 для детского сада
Числа от 11 до 20 для детского сада
Учебная программа Mindful Math для детского сада
Числа до 10 для первого класса
Числа до 20 для первого класса
Учебная программа Mindful Math для первого класса
Бесплатные головоломки со смыслом до 20
Подготовьте этот забавный набор числовых головоломок для своих учебных центров и помогите детям построить свое число смысл!
Возьмите 20 БЕСПЛАТНЫХ числовых головоломок с разными изображениями на каждой части, щелкнув изображение ниже .
Книги Number Sense
I Spy Numbers Jean Marzollo
1,2,3 Горох от Кита Бейкера
ChickaChicka 1,2,3 от Билла Мартина-младшего
Всплеск! Автор Энн Джонас (счет)
Очень голодная гусеница Эрик Карл (счет)
Как динозавры считают до 10? Джейн Йолен
Число повсюду Эллиот Кауфман
10 черных точек Дональд Крюс
Сколько жуков в коробке? Дэвид Картер
Сколько улиток? Пол Гиганти-младший.
Десять хитрых пираний, Уильям Уайз.
Нет числа, Оливер Джефферс.0339 «Больше или меньше» Стюарта Мерфи
Tally O’Mally Стюарта Мерфи
Местное значение Дэвида Адлера
Что такое местное значение Ширли Дьюк
Шарлатанство и счет Кита Бейкера
Держу пари! Стюарт Дж. Мерфи
Материалы для распознавания чисел
Попробуйте комплексную программу Mindful Math
Прочитайте о программе Mindful Math и о том, как она может положительно повлиять на ваш математический блок! Эта всеобъемлющая учебная программа по математике доступна для детского сада, первого и второго класса.
Узнайте больше об обучении. Серия
Подпишитесь на серию электронных писем, посвященных номеру здания, наполненных эффективными стратегиями, обязательными заданиями и БЕСПЛАТНЫМИ ресурсами для создания распорядка в вашем классе. Все, что вам нужно, чтобы помочь детям развить их чувство числа и в то же время весело провести время!
Имя
Личный адрес электронной почты
Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.
Я хочу получить бесплатный курс по электронной почте.
Эта форма собирает информацию, которую я буду использовать для отправки еженедельных электронных писем со стратегиями, рекламными акциями и ресурсами. Отписаться в любое время. Работает на ConvertKit
задачи по математике для 1 класса | Воспитание детей
Помните головоломки с фигурами, с которыми играл ваш ребенок, — используя треугольники для создания квадратов и прямоугольников? Оказывается, это была хорошая практика для решения математических задач в первом классе.
К концу первого класса математики ваш ребенок должен освоить 11 ключевых навыков:
- Счет до 120 — начиная с любого места, например, с 3 или 72.
- Сложение и вычитание чисел до 20.
- Зная, что этот знак «=» означает равенство.
- Решение текстовых задач с тремя однозначными числами (например, 2 + 3 + 9), сумма которых не превышает 20.
- Понимание того, почему сложение и вычитание обратны друг другу.
- Сложение до 100, включая сложение двузначного числа и однозначного числа (например, 82 + 7).
- Знать, как складывать двузначные числа на основе разрядности.
- Сложение или вычитание 10 с помощью вычислений в уме (например, 31 плюс 10 равно 41).
- Начал измерять вещи, например, выяснять, сколько его следов может поместиться в след его отца.
- Указание и запись времени с точностью до часа и получаса (например, 13:00 и 13:30).
- Объединение двух фигур для создания новой фигуры и разделение фигур на две и четыре части.

Математика в первом классе: Счет
Счет до 100 — это для дошкольников. Первоклассники считают до 120, но загвоздка в том, что они могут начать с любого числа, например 72, и досчитать до 73, 74, 75 и т. д. Дети также учатся вычитать числа до 20, например 19 – 7 = 12. Учащиеся учатся решать текстовые задачи, используя предметы, рисунки и, да, даже уравнения. Например, если у Теда 4 карандаша, у Даниэлы 6 карандашей, а у Вики 9.карандаши, сколько карандашей у них всего вместе?
Ваша первоклассница может сначала нарисовать эту задачу и сосчитать карандаши, но к концу года она будет знать уравнение и то, как его решать.
Первоклассники также узнают взаимосвязь между счетом, сложением и вычитанием. Например, считать от 1 до 2 — это то же самое, что складывать 1 + 1. Добавление еще одного означает увеличение на один, добавление еще двух означает увеличение на два и так далее. Точно так же вычитание можно рассматривать как обратный отсчет. Сделав еще один шаг вперед, дети учатся думать о вычитании как об обратном или «отмене» сложения. Так, например, если 15+4=19, тогда 19 – 4 = 15.
Так, например, если 15+4=19, тогда 19 – 4 = 15.
Математика в первом классе: разрядность
В детском саду ваш ребенок начал изучать разрядность, используя десятки и единицы. В двузначном числе, таком как 19, 1 представляет десятки, а 9 — единицы. Теперь ваш первоклассник будет опираться на это, научившись складывать двузначное число, например 54, и однозначное число, например 5, или двузначное число, кратное 10, например 10, 20, 30, 40 и т. д.
Одна из стратегий, которую выучит ваш ребенок, состоит в том, чтобы складывать десятки и единицы по отдельности.
Например: 54 + 5 = 50 + 0 = 50 и 4 + 5 = 9 итого 59.
А иногда приходится из единиц составить десятку.
Например: 54 + 7 = 50 + 0 = 50 и 4 + 7 = 10 + 1. Переместите 10 в десятки, так что 50 + 10 = 60 и 1, всего 61.
Ожидается, что ваш ребенок также сообразит в уме — не считая — как найти на 10 больше или меньше другого числа. Если у Джеммы есть 68 леденцов на палочке, и она отдает 10, она должна знать, что это то же самое, что вычесть одну группу десятков, и у нее останется 58 леденцов на палочке.
Математика для первоклассников: измерение
Первоклассники должны уметь объяснить длину двух предметов, сравнивая их с третьим предметом. Например, первый лист бумаги короче второго, но длиннее третьего.
Дети начинают применять концепцию сложения для измерения вещей. Допустим, ваш ребенок измеряет длину одеяла по собачьему хвосту; он может обнаружить, что одеяло имеет длину 5 с половиной хвостов. Это отличная практика, когда дети начинают использовать линейки.
Первоклассники также учатся определять время (и правильно записывать его, например, 13:30) с точностью до часа и получаса, считывая как электронные часы, так и старомодные круглые часы с минутной и часовой стрелками.
Математика для первоклассников: фигуры
Первоклассники изучают свойства фигур, объединяя две фигуры в новую, например, соединяя два треугольника, чтобы получить квадрат или прямоугольник. Они будут делать это на бумаге (двухмерное) и с предметами (трехмерное).
Дети также учатся делить фигуры на две или четыре равные части и учат слова, обозначающие эти части: половинки и четверти (или четверти).
20 Моделирование | R Programming for Data Science
20.1 Генерация случайных чисел
Посмотрите видео этого раздела
Моделирование — важная (и большая) тема как для статистики, так и для множества других областей, где необходимо ввести случайность. Иногда вам нужно реализовать статистическую процедуру, которая требует генерации или выборки случайных чисел (например, цепь Маркова Монте-Карло, бутстрап, случайные леса, бэггинг), а иногда вы хотите смоделировать систему, и для моделирования случайных входных данных можно использовать генераторы случайных чисел.
R поставляется с набором генераторов псевдослучайных чисел, которые позволяют моделировать известные распределения вероятностей, такие как нормальное, пуассоновское и биномиальное. Некоторые примеры функций для вероятностных распределений в R
-
rnorm: генерировать случайные нормальные переменные с заданным средним значением и стандартным отклонением -
dnorm: оценить нормальную плотность вероятности (с заданным средним/стандартным отклонением) в точке (или векторе точек) -
пнорм: оценить кумулятивную функцию распределения для нормального распределения -
rpois: генерировать случайные вариации Пуассона с заданной скоростью
Для каждого распределения вероятностей обычно доступны четыре функции, которые начинаются с букв «r», «d», «p» и «q». Функция «r» — это та функция, которая фактически моделирует случайные числа из этого распределения. Другие функции имеют префикс
Функция «r» — это та функция, которая фактически моделирует случайные числа из этого распределения. Другие функции имеют префикс
-
dдля плотности . -
rдля генерации случайных чисел -
рдля накопительной раздачи -
qдля квантильной функции (обратное кумулятивное распределение)
Если вы заинтересованы только в моделировании случайных чисел, вам, скорее всего, понадобятся только функции «r», а не другие. Однако, если вы собираетесь моделировать произвольные распределения вероятностей, используя что-то вроде выборки отбраковки, вам понадобятся и другие функции.
Вероятно, наиболее распространенным распределением вероятностей, с которым можно работать, является нормальное распределение (также известное как гауссово). Для работы с нормальным распределением необходимо использовать следующие четыре функции:
dnorm(x, mean = 0, sd = 1, log = FALSE) pnorm(q, среднее = 0, sd = 1, нижний.хвост = ИСТИНА, log.p = ЛОЖЬ) qnorm(p, среднее = 0, sd = 1, нижний.хвост = ИСТИНА, log.p = ЛОЖЬ) rnorm(n, mean = 0, sd = 1)
Здесь мы моделируем стандартные нормальные случайные числа со средним значением 0 и стандартным отклонением 1,
> ## Имитация стандартных нормальных случайных чисел > х <- rнорм(10) > х [1] 0,01874617 -0,18425254 -1,37133055 -0,59916772 0,29454513 0,38979430 [7] -1,20807618 -0,36367602 -1,62667268 -0,25647839
Мы можем изменить параметры по умолчанию для имитации чисел со средним значением 20 и стандартным отклонением 2.
> x <- rnorm(10, 20, 2) > х [1] 22,20356 21,51156 19,52353 21,97489 21,48278 20,17869 18,09011 19,60970 [9] 21,85104 20,96596 > резюме(х) Мин. 1 кв. Медиана Среднее 3-е кв. Макс. 18.0919,75 21,22 20,74 21,77 22,20
Если вы хотите узнать, какова вероятность того, что случайная переменная Normal будет меньше, скажем, 2, вы можете использовать функцию pnorm() для выполнения этого вычисления.
> пнорм(2) [1] 0,9772499
Никогда не знаешь, когда этот расчет пригодится.
20.2 Установка начального числа случайных чисел
При моделировании любых случайных чисел необходимо установить начальное число случайных чисел . Установка начального числа случайного числа с set.seed() обеспечивает воспроизводимость последовательности случайных чисел.
Например, я могу сгенерировать 5 нормальных случайных чисел с помощью rnorm() .
> сет.сид (1) > норм(5) [1] -0,6264538 0,1836433 -0,8356286 1,5952808 0,3295078
Обратите внимание, что если я снова вызову rnorm() , я, конечно, получу другой набор из 5 случайных чисел.
> норм(5) [1] -0,8204684 0,4874291 0,7383247 0,5757814 -0,3053884
Если я хочу воспроизвести исходный набор случайных чисел, я могу просто сбросить начальное число с помощью set.seed() .
> сет.сид (1) > rnorm(5) ## То же, что и раньше [1] -0,6264538 0,1836433 -0,8356286 1,5952808 0,3295078
В общем, всегда следует устанавливать начальное число случайных чисел при проведении моделирования! В противном случае вы не сможете восстановить точные числа, полученные в результате анализа.
Можно генерировать случайные числа из других вероятностных распределений, таких как Пуассон. Распределение Пуассона обычно используется для моделирования данных, которые поступают в виде подсчетов.
> rpois(10, 1) ## Считает со средним значением 1 [1] 0 0 1 1 2 1 1 4 1 2 > rpois(10, 2) ## Считает со средним значением 2 [1] 4 1 2 0 1 1 0 1 4 1 > rpois(10, 20) ## Считает со средним значением 20 [1] 19 19 24 23 22 24 23 20 11 22
20.3 Моделирование линейной модели
Посмотрите видео этого раздела
Моделирование случайных чисел полезно, но иногда мы хотим смоделировать значения, полученные из конкретной модели . Для этого нам нужно указать модель, а затем смоделировать ее с помощью функций, описанных выше. 92)\), \(\бета_0=0,5\) и \(\бета_1=2\). Переменная x может представлять собой важный предиктор исхода y . Вот как мы могли бы сделать это в R.
> ## Всегда устанавливайте начальное число! > сет.сид(20) > > ## Моделирование переменной-предиктора > х <- rнорм(100) > > ## Имитация термина ошибки > e <- rnorm(100, 0, 2) > > ## Вычислить результат с помощью модели > у <- 0,5 + 2 * х + е > резюме (у) Мин. 1 кв. Медиана Среднее 3-е кв. Макс. -6,4084 -1,5402 0,67890,6893 2,9303 6,5052
Мы можем построить результаты моделирования модели.
> plot(x, y)
Что, если мы хотим смоделировать предикторную переменную x , которая является двоичной, а не имеет нормальное распределение. Мы можем использовать функцию rbinom() для моделирования двоичных случайных величин.
> сет.сид (10) > x <- rbinom(100, 1, 0,5) > str(x) ## 'x' теперь равно 0 и 1 int [1:100] 1 0 0 1 0 0 0 0 1 0 ...
Затем мы можем продолжить работу с остальной частью модели, как и раньше.
> е <- rнорма(100, 0, 2) > у <- 0,5 + 2 * х + е > plot(x, y)
Мы также можем смоделировать обобщенную линейную модель , где ошибки больше не из нормального распределения, а из какого-то другого распределения. Например, предположим, что мы хотим смоделировать лог-линейную модель Пуассона, где
Например, предположим, что мы хотим смоделировать лог-линейную модель Пуассона, где
\[ Y \sim Пуассон(\mu) \]
\[ \log \mu = \beta_0 + \beta_1 x \]
и \(\beta_0=0,5\) и \(\beta_1=0,3\). Нам нужно использовать rpois() функция для этого
> set.seed(1) > > ## Имитация переменной-предиктора, как и раньше > x <- rnorm(100)
Теперь нам нужно вычислить среднее логарифмическое значение модели, а затем возвести его в степень, чтобы среднее значение передавалось в rpois() .
> лог.мю <- 0,5 + 0,3 * х > y <- rpois(100, exp(log.mu)) > резюме (у) Мин. 1 кв. Медиана Среднее 3-е кв. Макс. 0,00 1,00 1,00 1,55 2,00 6,00 > график (х, у)
Подобные модели можно строить произвольной сложности, моделируя больше предикторов или выполняя преобразования этих предикторов (например, возведение в квадрат, логарифмическое преобразование и т. д.).
20.4 Случайная выборка
Посмотрите видео этого раздела
Функция sample() случайным образом выбирает из указанного набора (скалярных) объектов, что позволяет вам выбирать из произвольного распределения чисел.
> сет.сид (1) > образец (1:10, 4) [1] 9 4 7 1 > образец (1:10, 4) [1] 2 7 3 6 > > ## Не обязательно числа > образец (буквы, 5) [1] «р» «с» «а» «у» «ш» > > ## Сделать случайную перестановку > образец (1:10) [1] 10 6 92 1 5 8 4 3 7 > образец (1:10) [1] 5 10 2 8 6 1 4 3 9 7 > > ## Образец с заменой > образец (1:10, заменить = ИСТИНА) [1] 3 6 10 10 6 4 4 10 9 7
Для выборки более сложных вещей, таких как строки из фрейма данных или списка, вы можете выбирать индексы в объект, а не элементы самого объекта.
Вот как можно выбирать строки из фрейма данных.
> библиотека (наборы данных) > данные (качество воздуха) > голова (качество воздуха) Ozone Solar.R Температура ветра Месяц День 1 41 190 7,4 67 5 1 2 36 118 8,0 72 5 2 3 12 149 12,6 74 5 3 4 18 313 11,5 62 5 4 5 НП НП 14,3 56 5 5 6 28 NA 14.9 66 5 6
Теперь нам просто нужно создать индексный вектор, индексирующий строки фрейма данных, и сделать выборку непосредственно из этого индексного вектора.
> набор семян(20)
>
> ## Создать индексный вектор
> idx <- seq_len(nrow(качество воздуха))
>
> ## Выборка из индексного вектора
> образец <- образец (idx, 6)
> качество воздуха [samp, ]
Ozone Solar.R Температура ветра Месяц День
107 н/д 64 11,5 798 15
120 76 203 9,7 97 8 28
130 20 252 10,9 80 9 7
98 66 НП 4,6 87 8 6
29 45 252 14,9 81 5 29
45 NA 332 13,8 80 6 14 Таким способом можно семплировать и другие более сложные объекты, если существует способ индексации подэлементов объекта.
20.5 Резюме
- Создание выборок из конкретных вероятностных распределений может быть выполнено с помощью функций «r»
- Встроены стандартные распределения: нормальное, пуассоновское, биномиальное, экспоненциальное, гамма и т. д.
- Функцию
sample()можно использовать для получения случайных выборок из произвольных векторов - Установка начального числа генератора случайных чисел с помощью
set.seed()имеет решающее значение для воспроизводимости
11 1Б: Лаборатория 4 | Навыки работы с данными 1-го уровня
11.
 1 Предварительные занятия
1 Предварительные занятияДля вашего последнего занятия перед занятием 1-го уровня (ура!) мы собираемся представить несколько новых функций, чтобы показать вам некоторые другие вещи, которые R может делать и которые будут также укрепить ваше понимание вероятности.
11.1.1 Моделирование
Одной из самых мощных функций R является то, что вы можете использовать его для моделирования данных. Моделирование данных — это процесс генерации случайных чисел, которые следуют определенному распределению или имеют известные свойства. Это может показаться не особенно впечатляющим, но моделирование данных означает, что вы можете делать такие вещи, как планирование статистического анализа, понимание и демонстрация того, как работает вероятность, или оценивать, сколько участников вам нужно протестировать в своем эксперименте, основываясь на том, что, по вашему мнению, будут данные. выглядит как. Моделирование данных использует различные типы распределений, которые мы рассмотрели в лабораторной работе 3, для генерации данных, поэтому убедитесь, что вы довольны главой о вероятностях, прежде чем двигаться дальше.
11.1.2 Упражнение 1:
sample() Как и в лабораторной работе 3, все функции, необходимые для симуляции, содержатся в Base R, однако мы также загрузим tidyverse , чтобы иметь возможность обрабатывать наши смоделированные данные.
Давайте начнем с введения функции sample() , которая выбирает элементы (точки данных) из вектора (коллекции объектов одного типа, таких как числа или слова). Мы можем использовать sample() для имитации подбрасывания монеты и построения некоторых графиков, которые вы видели в главе о вероятностях. sample() используется, когда мы хотим имитировать дискретные данные, то есть номинальные или порядковые данные.
sample() требует, чтобы вы определили три аргумента:
x= вектор элементов, т. е. все возможные результаты. Для нашего текущего примера это будут HEADS и TAILS.размер= сколько образцов вы хотите взять, т. е. сколько раз вы хотите, чтобы R подбрасывал монету?
е. сколько раз вы хотите, чтобы R подбрасывал монету? replace= указывает, следует ли сэмплировать с заменой или нет. В последней лабе мы использовали пример вытаскивания имен из шляпы. Если вы будете возвращать имя в шапку каждый раз, когда вытаскиваете его, это будет с заменой, если вы не вернете имя в шапку, это будет выборка без замены. По сути, вы хотите иметь возможность получить один и тот же результат на разных образцах? Для подбрасывания монеты должна быть возможность получить один и тот же результат более одного раза, поэтому мы указываемИСТИНА. Если бы мы указалиFALSE, вы могли бы нарисовать столько образцов, сколько было уникальных значений, поэтому в нашем случае мы могли бы подбросить монету только дважды: один раз она упадет орлом, один раз - решкой, а затем у нас закончатся результаты. .Откройте новый документ R Markdown, назовите его «Pre-class 4» и сохраните его в папке Psych 1B.

Скопируйте, вставьте и запустите приведенный ниже код в новом фрагменте кода, чтобы имитировать подбрасывание монеты 4 раза (и загрузить
tidyverse).
# Обратите внимание, что поскольку наши метки событий представляют собой строки (текст),
# нам нужно ввести их в функцию в "кавычках"
библиотека (tidyverse)
sample(x = c("HEADS", "TAILS"), size = 4, replace = TRUE) ## [1] "HEADS" "HEADS" "TAILS" "TAILS"
Сколько орлов вы получили ? Не волнуйтесь, если это отличается от нашего примера. Запустите код еще раз. Сколько голов вы получили на этот раз? Сколько вы получите за каждый ход, если запустите код еще пять раз?
При моделировании данных вы вряд ли получите один и тот же результат каждый раз, когда берете образец, точно так же, как если бы вы подбрасывали монету 4 раза в 5 отдельных случаях, вы вряд ли каждый раз получали бы одинаковое количество орлов. . Что особенно полезно в моделировании данных, так это то, что мы можем использовать результаты множества различных попыток выборки для расчета вероятности конкретного результата, например, получения 4 орлов при 4 бросках монеты.
Чтобы нам было проще складывать количество выпавших орлов и решек, давайте снова смоделируем подбрасывание монеты, но с использованием числовых кодов: 1 = ОРЕЛ, 0 = РЕШКА.
- Теперь, когда результаты являются числовыми, нам не нужна функция объединения
c - 0:1 означает все числа от 0 до 1 с шагом 1. То есть, в основном, 0 и 1. Если вы хотите имитировать бросок игральной кости, вы должны написать
1:6, что даст вам все числа от 1. до 6.
sample(x = 0:1, size = 4, replace = TRUE)
## [1] 0 1 1 0
11.1.3 Действие 2:
sum() Теперь, когда мы используем единицы и нули, мы можем подсчитать количество голов, суммируя значения результатов. В приведенном ниже коде будут сэмплированы наши подбрасывания монеты, как указано выше, а затем подсчитаны результаты. Поскольку мы закодировали орел = 1 и решку = 0, мы можем интерпретировать сумму всех результатов как количество орлов.
- Скопируйте, вставьте и запустите приведенный ниже код в новом фрагменте кода.
# Этот код направляет вывод sample() в sum(), который подсчитывает количество голов/1. sample(x = 0:1, size = 4, replace = TRUE) %>% sum()
## [1] 2
Запустите эту функцию несколько раз (вы можете использовать зеленую стрелку воспроизведения уценки в правом верхнем углу фрагмент кода, чтобы сделать это легко). В нашей симуляции пяти сетов по четыре флипа мы получили 1, 3, 2, 2 и 3 орла. Таким образом, только в одном из пяти симуляций мы получили ровно один орел, т. е. пропорцию 0,2 или 20% времени.
11.1.4 Действие 3:
replicate() 1 Давайте повторим эксперимент еще кучу раз. Мы можем заставить R делать это снова и снова, используя функцию replicate() . replicate() требует два аргумента (хотя есть и другие необязательные аргументы, если вы хотите выполнять более сложные задачи):
-
n= количество раз, которое вы хотите повторить свой код -
expr= выражение или код, который вы хотите повторить
Скопируйте, вставьте и запустите приведенный ниже код в новый фрагмент кода, чтобы запустить пример функции и суммировать результаты 20 раз.
повторение(n = 20, выражение = образец(0:1, 4, ИСТИНА) %>% сумма())
## [1] 1 3 4 1 1 1 2 3 1 2 1 2 2 3 4 1 1 2 3 2
11.1.5 Моделирование Монте-Карло
Каждый год город Монте-Карло становится местом бесчисленных азартных игр, в которые играют в его казино люди со всего мира. Эта дурная слава отражена в использовании термина «моделирование Монте-Карло» среди статистиков для обозначения использования компьютерного моделирования для оценки статистических свойств случайного процесса. В моделировании методом Монте-Карло случайный процесс повторяется снова и снова, чтобы оценить его эффективность в очень большом количестве испытаний. Обычно он используется в ситуациях, когда математические решения неизвестны или их трудно вычислить. Теперь мы готовы использовать симуляцию Монте-Карло, чтобы продемонстрировать вероятность различных исходов.
11.1.6 Действие 4:
replicate() 2 Мы снова проведем наш эксперимент с подбрасыванием монеты, но на этот раз мы проведем эксперимент 50 раз (каждый из которых включает 4 подбрасывания монеты) и используем те же принципы, чтобы предсказать количество решек, которые мы получим.
- Скопируйте, вставьте и запустите приведенный ниже код, чтобы запустить симуляцию и сохранить результат в объекте `heads50**, используя приведенный ниже код:
головы50 <- повторить(50, выборка(0:1, 4, ИСТИНА) %>% сумма()) головы50
## [1] 3 2 3 4 2 1 2 2 2 2 4 1 3 2 1 3 3 1 3 3 1 2 2 2 2 2 1 2 4 0 2 0 2 3 3 2 1 2 ## [39] 2 0 3 2 2 2 4 1 3 3 4 3
11.1.7 Действие 5: вероятность
Мы можем оценить вероятность каждого из исходов (0, 1, 2, 3, 4 орла после 4 подбрасывания монеты), подсчитав их и разделив на количество опытов. Мы сделаем это, поместив результаты репликации в tibble(), а затем используя count().
data50 <- tibble(heads = head50) %>% # преобразовать в таблицу
group_by(heads) %>% # группировка по количеству вариантов (0,1,2,3,4)
summarise(n = n(), # подсчитать количество случаев каждой возможности,
p=n/50) # & вычислить вероятность (p) каждой | 0 | 3 | 0,06 |
| 1 | 8 | 0,16 |
| 2 | 21 | 0,42 |
| 3 | 13 | 0,26 |
| 4 | 5 | 0,10 |
Ваши числа могут немного отличаться от представленных в этой книге — помните, что по умолчанию каждый раз, когда вы запускаете симуляцию, вы получаете другую случайную выборку.
11.1.8 Действие 6: визуализация
Затем мы можем построить гистограмму результатов, используя geom_bar() .
# Примечание: stat = "identity" указывает ggplot использовать значения переменной оси Y (p) в качестве высоты столбцов в нашей гистограмме (в отличие от подсчета количества вхождений этих значений) ggplot(data50, aes(x = головы, y = p)) + geom_bar (stat = "личность", fill = "фиолетовый") + labs(x = "Количество орлов", y = "Вероятность орла при 4 бросках (p)") + тема_минимальный()
Рисунок 11.1: Число выпавших орлов из 4 вероятностных исходов бросков монеты.
Сделайте здесь паузу и интерпретируйте приведенный выше рисунок
- Какова предполагаемая вероятность выпадения орла 0/4? 1/4 головы? 2/4 головы? 3/4 головы? 4/4 головы?
К сожалению, иногда этот расчет оценивает вероятность исхода как нулевую, поскольку этот исход никогда не возникал при запуске моделирования. Если вам нужны надежные оценки, вам нужен большая выборка , чтобы свести к минимуму вероятность того, что возможный результат не произойдет.
Если вам нужны надежные оценки, вам нужен большая выборка , чтобы свести к минимуму вероятность того, что возможный результат не произойдет.
11.1.9 Задание 7: большие данные
Давайте повторим моделирование Монте-Карло, но с 10 000 испытаний вместо 50. Все, что нам нужно сделать, это изменить n с 50 на 10 000.
head10K <- replicate( n = 10000, expr = sample(0:1, 4, TRUE) %>% sum())
Опять же, мы поместим результат в таблицу, используя tibble , и рассчитаем количество и вероятность каждого результата, используя group_by() и summarise() . Не забудьте попробовать прочитать свой код полными предложениями, чтобы помочь вам понять, что делают несколько строк кода, соединенных конвейерами. Как бы вы прочитали приведенный ниже код?
data10K <- tibble(головы = головы10K) %>%
group_by(головы) %>%
summarise(n = n(), p=n/10000) Наконец, мы можем визуализировать это, как делали ранее.
ggplot(data10K, aes(heads,p)) + geom_bar (stat = "личность", fill = "фиолетовый") + labs(x = "Количество орлов", y = "Вероятность орла при 4 бросках (p)") + тема_минимальный()
Рисунок 11.2: Вероятность подбрасывания 10 000 монет.
Используя моделирование методом Монте-Карло, мы оценили, что вероятность выпадения ровно одной решки при четырех бросках составляет около 0,25. Приведенный выше результат представляет собой распределение вероятностей для всех возможных исходов наших экспериментов. Отсюда мы можем извлечь много полезной информации.
Например, какова вероятность выпадения двух или более решек за четыре броска? Это легко: исходы, удовлетворяющие критерию, — 2, 3 или 4 орла. Мы можем просто сложить эти вероятности вместе вот так:
данные10K %>% фильтр (голов >= 2) %>% summarise(p2 = sum(p))
## # Таблица: 1 x 1 ## р2 ## <дбл> ## 1 0,687
Вы можете суммировать вероятности для различных исходов, если исходы являются взаимоисключающими, то есть когда происходит один исход, другие не могут произойти. В этом примере с подбрасыванием монеты это очевидно: вы не можете одновременно получить ровно два и ровно три орла в результате одного эксперимента. Однако имейте в виду, что вы не можете просто сложить вероятности вместе, когда рассматриваемые события не являются взаимоисключающими: например, вероятность того, что монета приземлится решкой вверх, и вероятность того, что монета приземлится с изображением головы, находящейся в определенной ориентации, являются не исключают друг друга и не могут быть просто сложены вместе.
В этом примере с подбрасыванием монеты это очевидно: вы не можете одновременно получить ровно два и ровно три орла в результате одного эксперимента. Однако имейте в виду, что вы не можете просто сложить вероятности вместе, когда рассматриваемые события не являются взаимоисключающими: например, вероятность того, что монета приземлится решкой вверх, и вероятность того, что монета приземлится с изображением головы, находящейся в определенной ориентации, являются не исключают друг друга и не могут быть просто сложены вместе.
Это основа того, как мы можем рассчитать вероятность исхода, используя известное распределение — моделируя большое количество испытаний, мы можем использовать это как оценку того, как наши данные будут выглядеть в реальном мире.
11.1.10 Упражнение 8:
rnorm() Мы также можем использовать R для моделирования непрерывных данных, которые следуют нормальному распределению, используя rnorm() . На самом деле вы уже использовали rnorm() раньше, еще в лабораторной работе 2 психоанализа 1A, но мы повторим это еще раз.
-
n— это количество точек данных, которые вы хотите смоделировать. Это единственный обязательный аргумент дляrnorm() -
означает, что- это среднее значение, которое вы хотите иметь для своих данных. Если вы не укажете этот аргумент,rnorm()будет использовать значение по умолчаниюmean = 0. -
sd— это стандартное отклонение, которое вы хотите иметь для своих данных. Если вы не укажете этот аргумент,rnorm()будет использовать значение по умолчанию 9.0012 сд = 1 .
Скопируйте, вставьте и запустите приведенный ниже код в новом фрагменте кода. Это случайным образом сгенерирует 50 чисел, которые в совокупности имеют среднее значение 10 и SD 2, а затем сохранит их в объекте normal .
нормальный <- rnorm(n = 50, среднее = 10, sd = 2)
Вы можете проверить, что сгенерированные вами данные соответствуют вашим ожиданиям, рассчитав среднее значение и стандартное отклонение этой новой переменной. значения должны быть ровно 10 и 2 (помните, что они генерируются случайным образом), но они должны быть достаточно близкими.
значения должны быть ровно 10 и 2 (помните, что они генерируются случайным образом), но они должны быть достаточно близкими.
среднее (нормальное) sd(нормальный)
## [1] 10.18396 ## [1] 1.811044
Наконец, вы можете визуализировать свои данные с помощью графика плотности. Попробуйте изменить количество точек данных, сгенерированных функцией rnorm() , с 50 до 500 и затем 5000, а затем посмотрите, как изменится форма распределения.
tibble(normal = normal) %>% #преобразовать переменную normal в таблицу и затем ggplot(aes(normal)) + # создать график плотности geom_density (заполнить = "красный") + тема_минимальный ()
Рисунок 4.4: Распределение переменной, созданной rnorm
11.1.11 Упражнение 9: Моделирование набора данных
Наконец, мы можем объединить все это для моделирования полного набора данных. Давайте представим, что мы собираемся провести эксперимент, чтобы посмотреть, выпадут ли 120 человек большее число на кубике, если их IQ выше. Это явно глупый эксперимент, но психология иногда делает глупости.
Это явно глупый эксперимент, но психология иногда делает глупости.
- Во-первых, давайте создадим переменную, содержащую все идентификаторы наших субъектов. Мы просто собираемся присвоить нашим участникам цифровые коды.
subject_id <- 1:120 # создайте переменную с именем subject_id, которая содержит числа от 1 до 120
Затем мы собираемся создать столбец для пола, используя новую, но простую функцию rep , которая означает «повторить». ». Приведенный ниже код создаст переменную, которая повторяет «мужчина» 40 раз, затем «женщины» 40 раз, а затем «недвоичный» 40 раз.
пол <- rep(x = c("мужчина", "женщина", "недвоичный"), каждый = 40) Далее, давайте смоделируем их всех, бросающих кубик один раз, используя образец() .
rolls <- sample(x = 1:6, size = 120, replace = TRUE)
Затем давайте смоделируем их IQ. Показатели IQ стандартизированы, так что в целом население имеет средний IQ 100 и SD 15, поэтому мы можем использовать эту информацию для моделирования данных с помощью rnorm() .
iq <- rnorm(n = 120, mean = 100, sd = 15)
Наконец, мы можем объединить все эти переменные в таблицу.
sim_data <- tibble(subject_id, пол, рулоны, iq)
Теперь, когда у нас есть смоделированные данные, мы можем написать код для их анализа еще до того, как мы соберем какие-либо реальные данные, что не только сэкономит нам время в будущем, но и поможет нам спланировать наши анализы, и мы могли бы включить это код в документе предварительной регистрации.
Например, вы можете создать график значений IQ для каждого броска костей (помните, что это не реальные данные…)
sim_data %>% mutate(rolls = as.factor(rolls)) %>% ggplot(aes(x = рулоны, y = iq, fill = рулоны)) + geom_violin (обрезка = ЛОЖЬ, альфа = .6, show.legend = ЛОЖЬ) + geom_boxplot (ширина = .2, show.legend = ЛОЖЬ) + scale_fill_viridis_d (опция = "E") + тема_минимальный() + labs(x = "Результат броска кубиков")
Рисунок 10.1: Блочная диаграмма показателей IQ, сгруппированных по тому, что выпал каждый человек на кубике.
11.1.12 Готово!
Занятия в классе для лабораторной работы 4 заключаются в анализе данных вашего группового проекта, что означает, что с точки зрения изучения нового материала мы закончили! В Psych 1A и 1B мы попытались дать вам исчерпывающее представление об общих навыках работы с данными, которые вам понадобятся для проведения собственных исследований. Даже если вы не собираетесь в будущем заниматься психологией или количественными исследованиями, мы надеемся, что вы гордитесь полученными навыками. Для некоторых из вас R, возможно, не был вашей любимой частью курса, но вы должны очень гордиться тем, чего вы достигли, и с таким разнообразным классом, мы надеемся, вы сможете увидеть, что программирование не является врожденным навыком, который только некоторые люди могут учиться. Нужно немного потрудиться, несколько (надеюсь) полезных учебных материалов и много ругательств на сообщения об ошибках.
11.2 Занятия в классе
Последние 6 месяцев мы потратили на то, чтобы дать вам навыки, необходимые для работы с вашими собственными данными. Пришло время показать нам, чему вы научились. В этой главе мы собираемся описать шаги, которые вам нужно будет выполнить при анализе ваших данных, но, кроме нескольких строк, которые помогут вам разобраться с данными анкеты, которые выдает платформа Experimentum, мы не собираемся дать вам любые кодовые решения.
Все, что вам нужно сделать, вы сделали раньше, так что используйте эту книгу, чтобы помочь вам. Помните, вам не нужно писать код по памяти, вам просто нужно найти соответствующие примеры, а затем скопировать, вставить и изменить то, что нужно изменить, чтобы он работал на вас.
Пришло время показать нам, чему вы научились. В этой главе мы собираемся описать шаги, которые вам нужно будет выполнить при анализе ваших данных, но, кроме нескольких строк, которые помогут вам разобраться с данными анкеты, которые выдает платформа Experimentum, мы не собираемся дать вам любые кодовые решения.
Все, что вам нужно сделать, вы сделали раньше, так что используйте эту книгу, чтобы помочь вам. Помните, вам не нужно писать код по памяти, вам просто нужно найти соответствующие примеры, а затем скопировать, вставить и изменить то, что нужно изменить, чтобы он работал на вас.
Мы предлагаем вам решить проблемы с кодом в группе, однако убедитесь, что у вас у всех есть отдельная копия окончательного рабочего кода.
11.2.1 Шаг 1: Загрузка пакетов и данных
Файлы данных находятся в Moodle. Помните, не делитесь ими в Messenger и т. д. из-за законов о защите данных.
Не изменяйте НИКАКОЙ код из шагов 1 и 2. Просто скопируйте и вставьте его в ТОЧНО, как показано ниже.
библиотека (tidyverse)
демо <- read_csv("demographics.csv")
mslq <- read_csv("mslq.csv")
команды <- read_csv("имя-команды.csv") 11.2.2 Шаг 2. Очистите данные
Запустите приведенный ниже код — ничего не меняйте. Этот код немного очистит данные Experimentum, чтобы помочь вам в пути. Вы получите сообщение о том, что NA введены путем принуждения . Не обращайте внимания на это сообщение, это результат преобразования часов работы в числовую переменную.
demo_final <- demo %>%
group_by(user_id, q_id) %>%
filter(session_id == min(session_id), endtime == min(endtime)) %>%
фильтр(номер_строки() == 1) %>%
разгруппировать() %>%
filter(user_status %in% c("гость", "зарегистрированный")) %>%
выберите (user_id, user_sex, user_age, q_name, dv) %>%
pivot_wider(names_from = q_name, values_from = dv)%>%
мутировать (занятость = as.numeric (занятость))
team_final <- команды %>%
group_by(user_id, q_id) %>%
filter(session_id == min(session_id), endtime == min(endtime)) %>%
фильтр(номер_строки() == 1) %>%
разгруппировать() %>%
filter(user_status %in% c("гость", "зарегистрированный")) %>%
выберите (user_id, user_sex, user_age, dv) %>%
переименовать("команда" = "дв")
mslq_final <- mslq %>%
group_by(user_id, q_id) %>%
filter(session_id == min(session_id), endtime == min(endtime)) %>%
фильтр(номер_строки() == 1) %>%
разгруппировать() %>%
filter(user_status %in% c("гость", "зарегистрированный")) %>%
выберите (user_id, user_sex, user_age, q_name, dv) %>%
упорядочить (q_name) %>%
pivot_wider(names_from = q_name, values_from = dv) Правильно. Твой ход. Помните, кодирование — это не запоминание кода, а знание того, где искать примеры, которые вы можете изменить с помощью ваших новых переменных. Возможно, вам будет полезно использовать функцию поиска в этой книге.
Твой ход. Помните, кодирование — это не запоминание кода, а знание того, где искать примеры, которые вы можете изменить с помощью ваших новых переменных. Возможно, вам будет полезно использовать функцию поиска в этой книге.
Рисунок 11.3: Поиск функций
11.2.3 Шаг 3: Объединить
Объединить файлы данных по их общим столбцам. В результирующем наборе данных будет 91 столбец, что означает, что R не покажет вам их все, если вы просто щелкнете по объекту, вам нужно будет запустить сводка() . Подсказка: Вы можете соединить только два объекта одновременно, поэтому вам нужно будет сделать несколько соединений (в конвейере, если вы чувствуете себя шикарно).
11.2.4 Шаг 4. Выберите свои переменные
Используйте select, чтобы сохранить только те переменные, которые вам нужны для выбранного плана исследования и анализа, т. е. ответы на интересующую вас подшкалу, а также идентификатор пользователя, пол, возраст, название команды и любые переменные, которые вы собираетесь использовать в качестве критериев для включения. Возможно, вам будет полезно обратиться к обзорному документу MSLQ из предварительного класса Lab 1, чтобы получить имена переменных.
Возможно, вам будет полезно обратиться к обзорному документу MSLQ из предварительного класса Lab 1, чтобы получить имена переменных.
11.2.5 Шаг 5: Коэффициенты
Используйте сводку или стр , чтобы проверить тип переменной в каждом столбце. Перекодируйте все необходимые переменные как факторы, а затем снова запустите сводку, чтобы увидеть, сколько у вас есть в каждой группе. Книга кодов, которую вы загрузили вместе с файлами данных из Moodle, поможет вам в этой задаче. Вы можете найти раздел Psych 1A о факторах, полезных для этого.
11.2.6 Шаг 6: Фильтрация
При необходимости используйте фильтр, чтобы сохранить только те наблюдения, которые вам нужны, например, вам может потребоваться удалить участников старше определенного возраста или использовать только зрелых учащихся и т. д. (и убедитесь, что вы сохранил все эти столбцы на шаге 4). Пока не фильтруйте данные для своей команды. Книга кодов, которую вы загрузили вместе с файлами данных из Moodle, поможет вам в этой задаче.
Если вашей группирующей переменной является наличие у студентов оплачиваемой работы, вам потребуется создать новую переменную с помощью mutate, которая распределяет участников по категориям работающих (> 0 часов в неделю) и неработающих (0 часов в неделю).
Дополнительный фрагмент синтаксиса, который может оказаться полезным для этого, — это нотация %in% , которая позволяет фильтровать по нескольким значениям. Например, следующий код сохранит все строки, где user_sex равно мужчинам ИЛИ женщинам и ничему другому (т. е. он избавится от небинарных участников, предпочитающих не говорить, и отсутствующих значений).
дата %>%
filter(user_sex %in% c("мужчина", "женщина")) Вы также можете сделать это путем исключения с помощью ! . Приведенный ниже код сохранит все, где user_sex не равно мужчине или женщине.
дат %>%
filter(!user_sex %in% c("мужчина", "женщина")) Если вам действительно хочется, вы можете выполнить шаги 3-6 в одном конвейере кода.
11.2.7 Шаг 7: Баллы по подшкалам
Подсчитайте средний балл для каждого участника по выбранной вами подшкале. Есть несколько способов сделать это, но полезно, чтобы документация Experimentum предоставила пример кода, чтобы сделать это проще, вам просто нужно адаптировать его для нужных вам переменных. Вы также можете изменить na.rm = TRUE для расчета средств в зависимости от того, хотите ли вы включить только участников, ответивших на все вопросы.
dat_means <- data %>% # изменить данные на имя объекта данных, с которым вы хотите работать pivot_longer(names_to = "var", values_to = "val", question_1:question_5) %>% # измените question_1:question_5 на соответствующие переменные для вашей подшкалы, больше ничего не меняйте group_by_at(vars(-val, -var)) %>% # вообще ничего не меняйте summarise(scale_mean = mean(val, na.rm = TRUE)) %>% # измените scale_mean на название вашей подшкалы, например, alarm_mean ungroup() # вообще ничего не меняйте
11.
 2.8 Шаг 8. Разделите набор данных
2.8 Шаг 8. Разделите набор данных Затем снова используйте фильтр, чтобы создать новый набор данных, содержащий только данные участников, внесших свой вклад в вашу команду, и назовите его dat_means_team . Как только это будет завершено, у вас будет окончательный большой набор данных, содержащий баллы по шкале для всех участников, и меньший набор данных, содержащий только данные от участников, которых вы наняли. Используйте кодовую книгу, чтобы найти, какой номер соответствует вашей команде.
11.2.11 Шаг 11: визуализация
Теперь вам нужно создать столбчатую диаграмму с планками погрешностей, диаграммой «скрипка-коробка» и сгруппированным графиком плотности как для полного набора данных, так и для набора данных вашей команды. Вы делали все это раньше, просто найдите предыдущий пример кода и измените переменные и метки осей.
Вам решать, как представить их в презентации. Возможно, вы захотите поместить все графики команды на один слайд, а затем все графики общего набора данных на другой.
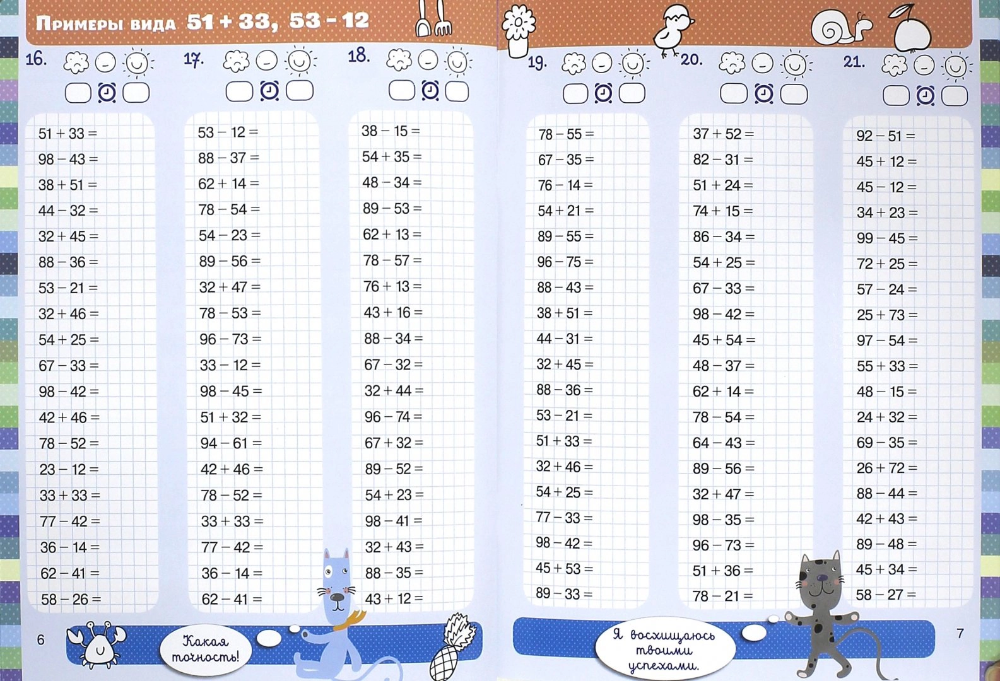
 50 примеров на лист. 8 листов.
50 примеров на лист. 8 листов.

 Сопоставление числовых карточек с десятью изображениями рамок является простым, но эффективным способом связи количества с числами.
Сопоставление числовых карточек с десятью изображениями рамок является простым, но эффективным способом связи количества с числами. Это отличная разминка для развития беглости перед уроками математики.
Это отличная разминка для развития беглости перед уроками математики. Поместите полоски в правильном порядке, чтобы открыть изображение.
Поместите полоски в правильном порядке, чтобы открыть изображение.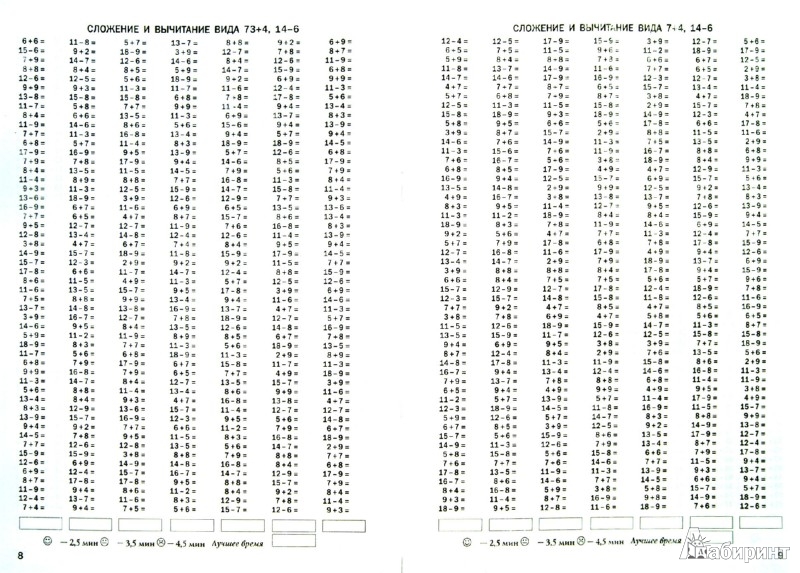
 ниже) являются полезными инструментами для использования и размещения на стене.
ниже) являются полезными инструментами для использования и размещения на стене.