Примеры для 3 класса по математике на умножение и деление столбиком: умножение многозначных чисел в столбик. Примеры с ответами. Скачать pdf или jpg.

Содержание

3 класс. Моро. Учебник №2. Ответы к стр. 106

Что узнали. Чему научились в 3 классе?

Умножение и деление

Ответы к стр. 106

1. Проверь, хорошо ли ты знаешь таблицы умножения и деления:

1) Вспомни, какие числа получаются при умножении 2, 3, 4 и т. д. на числа от 1 до 9, и продолжи ряды чисел.

5, 10, 15, 20, 25, 30, 35, 40, 45.
3, 6, 9, 12, 15, 18, 21, 24, 27.
6, 12, 18, 24, 30, 36, 42, 48, 54.
2, 4, 6, 8, 10, 12, 14, 16, 18.
7, 14, 21, 28, 35, 42, 56, 63.
9, 18, 27, 36, 45, 54, 63, 72, 81.
8, 16, 24, 32, 40, 48, 56, 64, 72.
4, 8, 12, 16, 20, 24, 28, 32, 36.

2) Объясни, как можно, используя таблицу умножения, найти частное.

54 : 9 = 6 32 : 8 = 4 56 : 7 = 8 18 : 2 = 9

3) Произведением каких двух однозначных множителей можно заменить числа: 64, 32, 63, 48, 27, 18, 24, 36, 56, 81?

8 • 8 = 64
4 • 8 = 32
7 • 9 = 63
6 • 8 = 48
3 • 9 = 27
2 • 9 = 18   3 • 6 = 18
4 • 6 = 24   3 • 8 = 24
6 • 6 = 36   4 • 9 = 36
7 • 8 = 56
9 • 9 = 81

4) Проверь, можешь ли ты правильно решить примеры каждого столбика за 2 мин (записывай только ответы).

4 • 3 = 12 6 : 2 = 3 7 • 8 = 56 27 : 3 = 9
6 • 5 = 30 12 : 4 = 3 3 • 6 = 18 56 : 8 = 7
9 • 7 = 63 36 : 9 = 4 7 • 7 = 49 15 : 5 = 3
6 • 8 = 48 42 : 6 = 7 8 • 9 = 72 64 : 8 = 8
2 • 9 = 18 25 : 5 = 5 4 • 5 = 20 36 : 6 = 6
8 • 4 = 32 24 : 3 = 8 9 • 3 = 27 81 : 9 = 9
9 • 5 = 45 32 : 4 = 8 5 • 8 = 40 12 : 3 = 4

7. Вспомни, как можно умножить сумму на число, и реши с устным объяснением.

27 • 4 = 20 • 4 + 7 • 4 = 108 32 • 3 = 30 • 3 + 2 • 3 = 96
18 • 5 = 10 • 5 + 8 • 5 = 90 17 • 4 = 10 • 4 + 7 • 4 = 68

8. Вспомни, как можно разделить сумму на число, и реши с устным объяснением.

46 : 2 = 40 : 2 + 6 : 2 = 23 84 : 7 = 70 : 7 + 14 : 7 = 12
96 : 3 = 90 : 3 + 6 : 3 = 32 96 : 4 = 80 : 4 + 16 : 4 = 24

ЗАДАНИЕ НА ПОЛЯХ:
Головоломка:

36 = 6 • 6
36 = 2 • 3 • 6
48 = 6 • 2 • 2 • 2

ГДЗ по математике. Учебник. 3 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 3 класс

Калькулятор дробей онлайн

Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».

Вид дроби: простые дроби смешанные дроби

Дробь 1		Дробь 2		Результат
	+−×÷		=


+/−		+/−

Вычислить

Решение:

Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.

Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной.

Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).

Пример:

= 2 +

Похожие калькуляторы

Сравнения дробей Сокращения дробей Возведение дроби в степень

Матрицы – умножение, деление, сложение и вычитание

Перейти к содержимому

Умножение

Деление

Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.

Умножить матрицу на одно число очень просто –

Вычисления выполняются по следующей формуле –

Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.

Умножение матрицы на другую матрицу

Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 ^st и столбца 1 ^st.

Скалярный продукт — это умножение совпадающих членов и их суммирование —

(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 ^и членов, таких как 2 и 9, и 3 ^и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.

Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —

(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74

Теперь мы можем сделать то же самое для 2 ^-й-й ряд и 1-й столбец –

(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12

И тогда для 2 ^-й строки и 2-го столбца –

(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11

Тогда мы окончательно получим результат.

Надеюсь, теперь вы разобрались с методом и решениями?

Дивизия

А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.

X / Y = X * (1/Y) = X * B ^-1

Где B обратная означает обратную матрицу B. Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.

Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.

После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.

Сложение и вычитание

Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры.

Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.

Давайте решим несколько примеров и разберемся в них глубже –

Пример – 1

[1 2] + [2 -3]

Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.

[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]

Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.

Пример – 2

[4 5] – [2 1]

Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –

[4 5] – [2 1]
= [4-2 5-1]
= [2 4]

Сложение матрицы очень простое и выполняется с каждой записью.

Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:

Добавьте следующие матрицы

Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.

Итак, окончательный ответ —

До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.

Оцените приведенную ниже задачу или, если это невозможно, укажите причину.

Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –

Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.

Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.

Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.

Найдите значения x и y для следующих уравнений –

Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –

, Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях

X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1

And

2y – 3 = -5
Y = -5 + 3 / 2

Y = -2 / 2
Д = -1

Перейти к началу

Как преподавать дивизион — простое пошаговое руководство

Дом
>
Блог
>
Как преподавать деление — простое пошаговое руководство

Джессика Камински

8 минут чтения

27 апреля 2022 г.

Деление является четвертым среди первых четырех основных математических операций, которые должен освоить ребенок. Эти математические операции сложения, вычитания, умножения и деления. Они составляют основу всех математических задач. Изучение первых трех операций не является обязательным для ребенка, чтобы понять деление, но, как мы увидим, они необходимы. Однако научить ребенка делению не так сложно, как может показаться.

Концепция деления

Как было сказано выше, деление может показаться сложным, но это проще, чем вы думаете. Как правило, разделение влечет за собой разделение поровну в соответствии с количеством необходимых групп. По этой причине вы можете связать разделение с идеей разделения поровну.

Например, несколько элементов могут поровну распределяться между группами. Практический пример: разделить 9 яблок (количество предметов) между 3 друзьями (3 группы), при этом у каждого друга будет 3 яблока.

Основная концепция деления лучше понимается с помощью методов группировки и совместного использования. Деление также называют обратным умножению или процессом многократного вычитания.

Как научить ребенка делению

Научиться делению или научить делению не так сложно, как кажется. Родитель или учитель может освоить простой подход к эффективному объяснению деления. Следовательно, ребенок может быстро понять концепцию довольно легко.

Ниже приведен пошаговый процесс обучения делению от базовой концепции деления до полного деления. Этот подход предполагает постепенный процесс, облегчающий оценку того, как ребенок справляется с проблемами деления.

Примечание. Крайне важно, чтобы ваше обучение было интересным и увлекательным, чтобы повысить его эффективность.

Шаг 1: Знакомство с основами деления

Чтобы ребенок понял деление, ему необходимо понять основы деления.

Во-первых, познакомьте ребенка с концепцией разделения как способом поделиться. Естественно, при таком подходе ребенку легче понять деление. Поэтому вводите для практики такие предметы, как конфеты.

Во-вторых, физически попросите ребенка разделить количество конфет на более мелкие группы. Например, если у вас есть 8 конфет, попросите ребенка разделить их на 4 небольшие равные группы. Это значит, что в каждой группе должно быть равное количество предметов (конфет). В этом случае 8 — это делимое (оно представляет общее количество элементов/объектов), а 4 — делитель. по 2 конфеты в каждой группе; следовательно, 8 разделить на 4 группы равно 2.

Когда-то ребенок научился группировать, теперь вы можете вводить символы деления. Для обозначения деления потребуется записать знак деления (÷) и косую черту (/). Кроме того, вы должны произнести это вслух, записывая на листе. Это делает процесс видимым для ребенка и улучшает понимание. Из приведенного выше сценария 8 разделить на 4 можно записать как 8÷4 или 8/4.

Теперь, если ребенок знает принцип умножения, ему будет еще проще объяснить деление. Вы поможете им понять, что деление противоположно умножению. Поэтому используйте таблицы умножения, чтобы проиллюстрировать этот процесс. Например, проверьте по таблице умножения 2×4 = 8, а затем проиллюстрируйте, что 8÷4= 2. Затем сделайте 2×3=6 и 6÷3=2. Вы должны делать это несколько раз, пока ребенок не поймет связь между умножением и делением.

Наконец, оцените способности вашего ребенка к обучению, дав ему несколько простых задач на деление. Однако убедитесь, что вы используете числа, которые делятся без остатка. Например, 12÷4, 6÷3, 8÷2, 15÷5 и т. д. Вы можете помочь им повторить этот шаг от разделения конфет на группы до использования таблицы умножения.

Шаг 2: Выработка деления с остатками

Если ребенок уже понимает основные деления, в том числе как делить числа нацело, вы можете перейти к следующему шагу. Этот шаг влечет за собой работу с остатками, где числа не могут быть разделены поровну.

Чтобы разработать концепцию остатков в делении, используйте такие предметы, как конфеты и кубики. Начните с подсчета определенного количества конфет, которые нельзя разделить на равные группы или разделить поровну.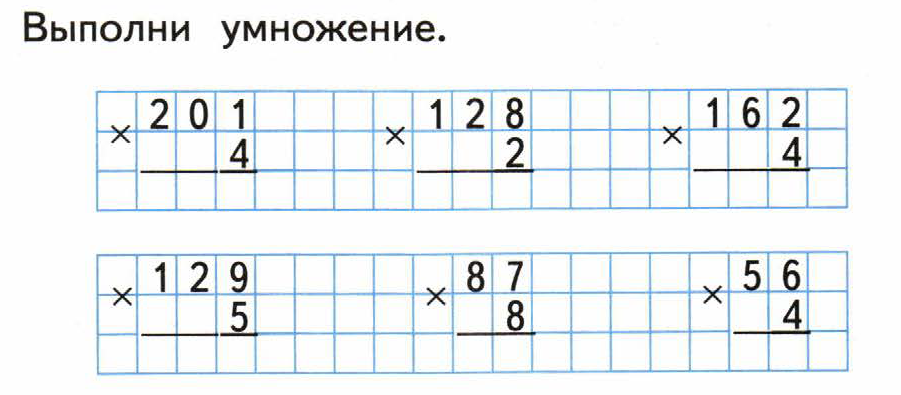 Например, попросите ребенка разделить 9 конфет на группы по 4 или разделить 15 конфет на группы по 6.

В первом сценарии остаток будет равен 1, потому что в каждой из 4 групп будет по две конфеты. Во втором примере останется 3 конфеты, потому что в каждой из 6 групп будет по 2 конфеты. Это понятие помогает ребенку понять, что некоторые числа остаются при делении и называются остатками.

Затем вы должны записать задачу на деление на листе. Например, 9÷4=2 остатка 1 и 15÷6=2 остатка 3.

Чтобы сделать обучение делению с остатком более эффективным, предложите ребенку больше задач на деление, таких как 7÷2, 10÷3, 15÷4, 20÷7, 25÷10 и т. д. Конечная цель состоит в том, чтобы ребенок/ученик тренировался до тех пор, пока он не сможет объяснить, почему у него есть остатки в каждой группе без вашей помощи. Вы можете разрешить им использовать конфеты или другие предметы, если им нужно сгруппироваться.

Шаг 3. Обучение делению на длинное деление

Как указывалось ранее, обучение детей делению — это постепенный процесс. Поэтому, если ребенок успешно справился с двумя предыдущими шагами, пора переходить на другой уровень, т. е. на деление в длину. Изучение длинного деления немного технично. Тем не менее, ребенок, который уже понимает основные операции, обратные таблице умножения и остаткам, может легко решить деление в столбик.

Обычно длинное деление повторяет основные шаги деления, умножения, вычитания и опускания до следующей цифры.

Чтобы научить детей делению на четные, начните знакомить их с понятием четного деления. Каждая сотня, десяток и единица без остатка делятся на делитель. Ребенок привыкает знать и упражняться, сколько раз делитель входит в различные цифры делимого.

Следующий шаг в делении в длинное число включает остаток и использует понятия умножения и вычитания. Вы применяете умножение и вычитание в самом простом месте в самом конце деления, то есть в той колонке, где у вас есть остаток. Однако, если у вас есть остаток в десятках в алгоритме длинного деления, вы делите, умножаете, вычитаете, а затем переходите к следующей цифре.

Разделить:

следовательно, мы получили 1 (размещено над длинным знаком деления). Мы также можем сказать, что 2 разделить на 2 равно 1.

Умножить и вычесть:

Теперь давайте вычислим оставшиеся 54.

2×2=4, запишем 4 под 5 и вычтем, чтобы найти остаток . Остаток 1 из 10.

Опустите следующую цифру

Затем опустите 4 цифры рядом с 1 из десяти оставшихся. Теперь у вас есть 14.

Теперь разделите два на 14. Повторится та же самая концепция умножения, где 2×7= 14. Запишите 7 над знаком деления и 14 под 14. Снова произойдет вычитание, в результате чего 14-14 =0

Следовательно, частное 254 на 2 равно 127.

Последняя мысль

Деление может быть трудным для изучения, особенно для детей, которые взаимодействуют с ним впервые. Тем не менее, описанный выше подход касается того, как шаг за шагом перейти от основ к полному делению. Самое главное, стоит отметить, что обучение детей делению — это постепенный процесс.