Примеры на деление 4 класс столбиком без остатка: примеры на умножение и деление 4 класс в столбик карточки: 16 тыс изображений найдено в Яндекс.Карти…

Деление трёхзначного числа на однозначное | Методическая разработка по математике (3 класс) по теме:

Опубликовано 18.03.2012 — 16:48 — Сикорская Валентина Аристафовна

Дидактический раздаточный материал для самостоятельной работы по математике

Скачать:

Предварительный просмотр:

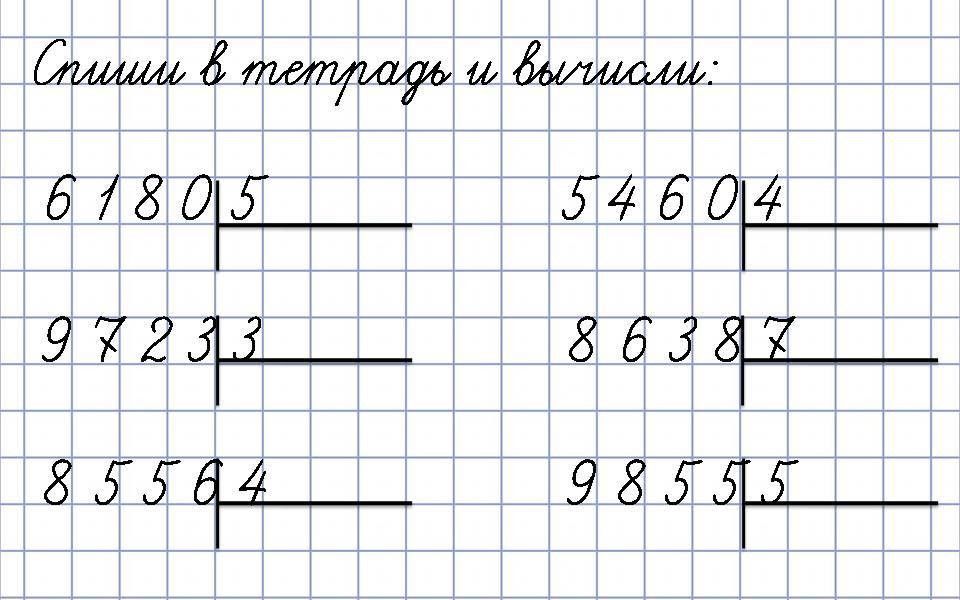
486 : 2

642 :2

693 : 3

848 : 4

 936 : 3

 264 : 2

 996 : 3

555 : 5

966 : 3

 484 : 4

488 : 2

963 : 3

 448 : 4

639 : 3

684 : 2

777 : 7

674 : 2

896 : 2

678 : 3

 892 : 4

 676 : 2

 954 : 3

490 : 2

 860 : 4

 580 : 5

 678 : 6

 896 : 8

798 : 7

 476 : 4

 687 : 3

 585 : 5

654 : 2

 876 : 4

298 : 2

 675 : 3

 468 : 4

595 : 5

 684 : 6

872 : 4

146 : 2

219 : 3

196 : 2

332 : 4

335 : 5

 288 : 4

 370 : 5

291 : 3

 408 : 8

 426 : 6

 330 : 6

 455 : 7

 567 : 7

 549 : 9

 684 : 9

504 : 8

 486 : 6

728 : 8

595 : 7

 531 : 9

168 : 4

189 : 3

 405 : 5

260 : 4

 232 : 4

504 : 6

592 : 8

 252 : 3

432 : 9

539 : 7

516 : 6

376 : 8

570 : 2

  672 : 4

 792 : 3

 828 : 6

 840 : 5

 936 : 6

 920 : 8

 912 : 4

 882 : 7

 965 : 5

 738 : 6

 801 : 3

708 : 4

 903 : 7

822 : 6

895 : 5

984 : 8

 852 : 6

 973 : 7

 936 : 4

875 : 5

572 : 4

855 : 3

 976 : 2

 918 : 6

 966 : 7

 992 : 8

792 : 3

 996 : 4

 894 : 6

889 : 7

952 : 8

612 : 2

927 : 3

540 : 5

828 : 4

648 : 6

921 : 3

742 : 7

963 : 9

864 : 8

745 : 5

 872 : 8

954 : 9

 536 : 8

 861 : 7

576 : 6

436 : 4

530 : 5

856 :  8

 648 : 6

836 : 4

972 : 9

 675 : 5

 954 : 6

896 : 7

Предварительный просмотр:

 

592 : 8

 252 : 3

432 : 9

539 : 7

516 : 6

376: 8

 672 : 4

 828 : 6

840 : 5

912 : 4

882 :7

570 : 2

 936 : 6

 920 : 8

828 : 6

 840 : 5

 936 : 6

 920 : 8

 

 278 х 3

 157 х 6

186 х5

124 х 8

 128 х 7

182 х 4

293 х 3

171 х5

 238 х 4

147 х 7

136 х 6 

374 х 2

204 х 3

103 х 8

107 х 6

 269 х 3

253 х 3

151 х 5

204 х 3

103 х 8

107 х 6

 269 х 3

374 х 2

128 х 7

По теме: методические разработки, презентации и конспекты

Математика.

Деление трёхзначного числа на двузначное

Дорогие ребята! В этой презентации вашему вниманию представлены тренировочные примеры на деление трёхзначных чисел на двузначные. Удачи!   Для скачивания нажмите «скачать»!…

3-4 класс, Интерактивная игра-тренажёр «Африка» (деление трёхзначного числа на однозначное)

Цель: отработка умения делить трёхзначное число на однозначное число.[[{«type»:»media»,»view_mode»:»media_large»,»fid»:»3188798″,»attributes»:{«alt»:»»,»class»:»media-image»,»height»:»351″,»width»:»46…

Карточка «Деление трёхзначного числа на однозначное»

Письменные приёмы деления…

Интерактивная игра «Деление трёхзначного числа на однозначное»

Интерактивная игра «Деление трёхзначного числа на однозначное» по математике создана для учащихся 3-4 класса, УМК любой. Игру можно использовать на этапе изучения или повторения в ходе …

Технологическая карта урока математики » Деление трёхзначного числа на однозначное » 3 класс

Технологическая карта разработана для урока математики по теме «Деление трёхзначного числа на однозначное » в 3 классе УМК «Школа 2100». …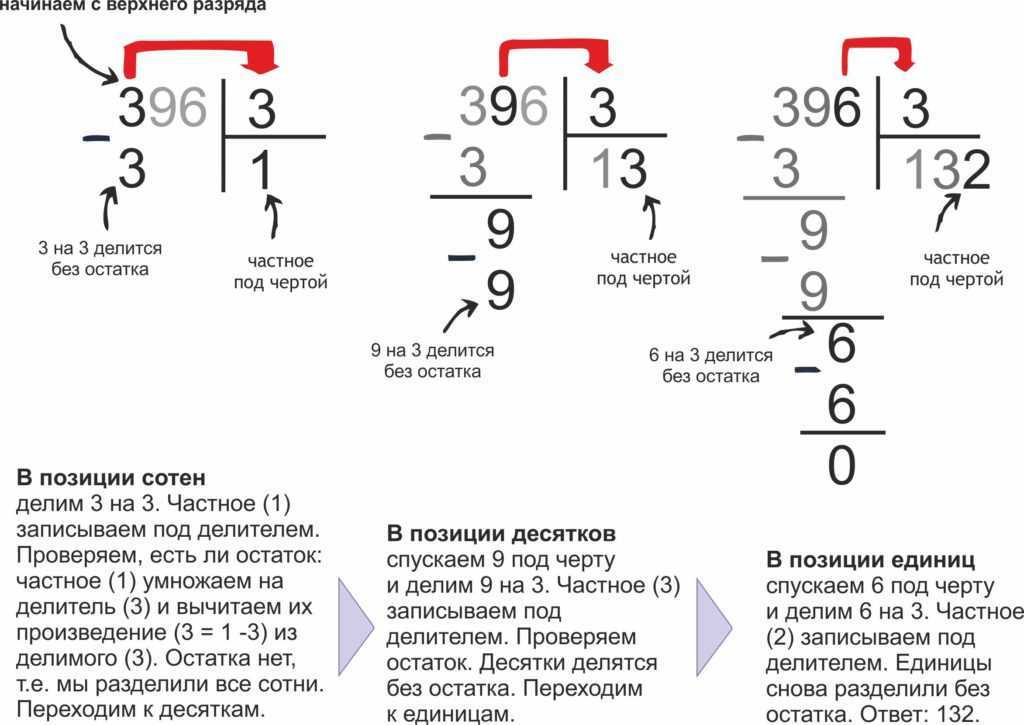

Интерактивная игра — Деление трёхзначного числа на однозначное

Интерактивная игра — Деление трёхзначного числа на однозначное…

Алгоритм письменного деления трёхзначного числа на однозначное.

Алгоритм письменного деления трёхзначного числа на однозначное. Математика 3 класс….

Поделиться:

 

Как объяснить ребенку деление столбиком: легко и доступно

Суть и принцип деления можно объяснить двумя способами: дошкольникам рассказать простыми словами, а младшим школьникам — математически. Обычно ребёнку сложно разобраться в операции деления, если он не понимает, как умножать числа, и путается в понятиях состава примера: «множитель», «сумма», произведение». В статье рассказываем, как родитель может объяснить деление доступно в зависимости от возраста ребёнка.

Как объяснить деление дошкольнику

Дети впервые сталкиваются с делением в раннем детстве, когда ещё не понимают, что значит «число». Малыш в песочнице слышит: «Поделись игрушкой», и он понимает, что ведёрко нужно отдать другу, а лопатку оставить себе. 

Основное правило для объяснения любого понятия малышам — показывать на жизненных примерах, при этом они должны соответствовать возрасту ребёнка. Поэтому дошкольникам лучше рассказывать, как делить игрушки и бананы, а не деньги и почтовые конверты.

Шаг 1. Делить без остатка

Есть десять конфет для мамы, папы, ребёнка, бабушки и дедушки. Нужно поделить конфеты так, чтобы у всех было одинаковое количество. Ребёнок будет раздавать всем по одной, пока они не закончатся. Становясь старше, он будет учиться раздавать сразу по две, три и более.

Шаг 2. Делить с остатком

Есть десять конфет для мамы, папы, ребёнка и бабушки. Дедушка отказался от сладкого. Ребёнок может раздать каждому по две конфеты, и  две останутся.

Шаг 3. Делить с остатком, который делится

Ребёнок может раздать всем членам семьи, кроме дедушки, по половинке конфеты, разделив две конфеты, от которых дедушка отказался. Тогда у каждого будет по две с половиной конфеты.

Шаг 4. Делить с остатком, который не делится

На двоих детей нужно разделить три мяча. Один невозможно разделить, и он просто останется.

Последние два шага помогут ребёнку разобраться с дробями в будущем.

<<Форма демодоступа>>

Как объяснить деление школьнику

Чтобы ребёнок освоил деление, ему нужно знать несколько понятий:

• «числа» и «разряды»;
• «делимое», «делитель», «частное»;
• «множитель», «произведение»;
• «обратное действие».

Шаг 1. Повторить, как делить поровну и с остатком

Если ребёнок не освоил простое деление, стоит повторить его.

Шаг 2. Объяснить обратное действие

До знакомства с делением дети осваивают операции сложения, вычитания и умножения. Младшие школьники уже понимают, что вычитание — это действие, обратное сложению: если к двум прибавить два, получим четыре; и наоборот, если из четырёх вычесть два, получим два.   Объясните ребёнку, что деление — это действие, обратное умножению. Произведение чисел можно разделить на один из множителей и получить второй множитель: например, если два умножить на два, получится четыре, и наоборот, при делении четырёх на два получится два. Чтобы умножать и делить числа, нужно знать таблицу умножения.

Шаг 3. Делить двузначное число на однозначное без остатка

Стоит брать числа бо́льшие, чем в таблице умножения. Например, последнее число, на которое умножается пять в таблице умножения, — это десять, и их произведение — 50. Значит, можно начинать с 55 и выше.

Если взять 55, то легко разделить каждый разряд числа на пять. Если взять, например, 60, то ситуация становится сложнее. Здесь на помощь могут прийти деление в столбик или строчку.

Как разделить 60 на 5:

1. Сначала делим число из разряда десятков, то есть шесть делим на пять. Важно, чтобы число в этом разряде было больше числа, на которое делим. То есть если нам необходимо 30 разделить на пять, не нужно делить десятки отдельно от единиц. Так как шесть не делится на пять без остатка, нужно найти ближайшее к шестёрке меньшее число, которое делится на пять без остатка, — это пять. При делении пятёрки на пять получаем единицу. Результат этого деления записываем после знака равенства: 60 : 5 = 1_.
2. Шестёрку раскладываем по составу на пятёрку, которую взяли для деления, и единицу. Эту единицу записываем над шестёркой или просто держим в уме.
3. Соединяем единицу, которую держали в уме, и цифру из разряда единиц в числе 60, то есть единицу и ноль. Получаем десять. При делении десяти на пятёрку получаем двойку, результат этого деления записываем после знака равенства за разрядом десятков.
4. Получаем: 60 : 5 = 12.

Шаг 4. Делить двузначное число на однозначное с остатком

Здесь принцип такой же, как и в предыдущем шаге: число делим в столбик или в строчку.

Как разделить 88 на 5:

1. Сначала делим число из разряда десятков, то есть восемь делим на пять. Важно, чтобы число в этом разряде было больше числа, на которое делим. Так как восемь не делится на пять без остатка, нужно найти ближайшее к восьмёрке меньшее число, которое делится на пять без остатка, — это пять. При делении пятёрки на пять получаем единицу. Результат этого деления записываем после знака равенства: 88 : 5 = 1_.
2. Восемь раскладываем по составу на пятёрку, которую взяли для деления, и тройку. Эту тройку записываем над восьмёркой или просто держим в уме.
3. Соединяем тройку, которую держали в уме, и цифру из разряда единиц в числе 88, то есть три и восемь. 38 на пять не делится, ищем меньшее ближайшее число, делимое на пять без остатка, — это число 35. 35 : 5 = 7, результат записываем после знака равенства после разряда десятков: 88 : 5 = 17.
4. 38 раскладываем по составу, то есть на 35 и три. Так как три не делится на пять, берём взаймы ноль и ставим запятую в частном: 17,_. Соединяем три и ноль, получаем 30. При делении тридцати на пятёрку получаем шесть. Результат этого деления записываем после знака равенства после запятой.
5. Получаем: 88 : 5 = 17,6.

Как только ребёнок освоит навык, можно усложнять задания: делить трёх-, четырёхзначные числа на однозначное с остатком и без него.

Шаг 5. Делить трёхзначное число на двузначное с остатком и без него

Принцип деления такой же, как и выше, но нужно делить уже на двузначное число.

Как разделить 100 на 20:

Число в разряде сотен меньше делителя. Смотрим на число, составляющее разряды сотен и десятков, оно тоже меньше делителя, поэтому берём всё число сразу. Подбором находим частное: 100 : 20 = 5.

Как разделить 104 на 32:

1. В этом примере нам нужно взять всё число целиком. Оно делится с остатком, поэтому подбираем ближайшее к 104 меньшее число. 96 : 32 = 3, результат записываем после знака равенства: 104 : 32 = 3_.
2. 104 раскладываем по составу, то есть на 96, которую взяли для деления, и восемь. Восемь на 32 не делится, поэтому берём взаймы ноль и ставим запятую в частном: 3,_. Соединяем восемь и ноль, получаем: 80 : 32. Число 80 не делится на 32 без остатка, поэтому подбираем ближайшее к 80 меньшее число, делимое на 32 без остатка, — это 64. 64 : 32 = 2, результат записываем после знака равенства после запятой: 104 : 32 = 3,2_.
3. 80 раскладываем по составу, то есть на 64, которую взяли для деления, и 16. 16 на 32 не делится, и оно меньше делителя, поэтому берём взаймы к 16 ноль. Получаем: 160 : 32 = 5,  результат записываем после знака равенства после запятой в разряде сотых.
4. Получаем: 104 : 32 = 3,25.

Альтернативные варианты

Группировка

Чтобы разделить 30 на три, можно представить 30 мистеров Фоксов и считать тройками, то есть тем числом, на которое будем делить. В группе из 30 мистеров Фоксов получится десять групп по три мистера Фокса. Значит, 30 : 3 = 10.

30 мистеров Фоксов, где обведено по три мистера.

<<Форма аттестации>>

Разложение

Чтобы разделить 90 на три, можно представить 90 в виде суммы чисел, каждое из которых точно делится на три.

Подбор

Чтобы разделить 96 на 12, нужно подбирать числа, пока не получим восемь: 96 : 12 = 8.

Иллюстрация: justyna stasik / Dribbble

Определение, Как найти множители числа? Примеры

Коэффициент числа в математике представляет собой делитель данного числа, который делит его полностью, не оставляя остатка. Чтобы найти делителя числа , мы можем использовать различные методы, такие как метод деления и метод умножения. Факторы используются в реальных жизненных ситуациях, когда нам нужно что-то разделить на равные строки и столбцы, сравнить цены, обменять деньги и так далее. Давайте узнаем больше о факторах и как найти делители числа в этой статье.

1.	Что такое факторы?
2.	Свойства факторов
3.	Как найти делители числа?
4.	Нахождение числа факторов
5.	Часто задаваемые вопросы о дробях

Что такое факторы?

В математике множитель — это число, которое полностью делится на другое число без остатка. Факторы и множители являются частью нашей повседневной жизни. Например, они используются при раскладывании предметов в коробке, работе с деньгами, поиске закономерностей в числах, решении соотношений и работе с дробями.

Коэффициент Определение

Множитель числа — это число, на которое данное число полностью делится без остатка. Факторы числа могут быть положительными или отрицательными. Например, давайте найдем делители числа 8. Поскольку 8 делится на 1, 2, 4 и 8, мы можем перечислить положительные делители числа 8 как 1, 2, 4 и 8. Помимо этого, число 8 имеет также отрицательные факторы, которые могут быть перечислены как -1, -2, -4, -8, потому что произведение двух отрицательных чисел является положительным числом, что означает (-1) × (-8) = 8, и ( -2) × (-4) = 8.

Однако мы обычно используем только положительные множители числа. Давайте прочитаем о некоторых свойствах факторов.

Свойства факторов

Делители числа обладают следующими свойствами:

• Число делителей числа конечно.
• Множитель числа всегда меньше или равен заданному числу.
• Каждое число, кроме 0 и 1, имеет как минимум два делителя: 1 и само число.
• Деление и умножение — это операции, которые используются для нахождения делителей числа.

Как найти делители числа?

Чтобы найти делители числа, мы можем использовать метод деления и метод умножения. Давайте прочитаем об этих методах в следующих разделах.

Нахождение множителей с помощью метода деления

Найдем множители числа с помощью метода деления.

Пример: Найдите множители числа 12, используя метод деления.

Решение: Давайте найдем множители числа 12, используя следующие шаги.

• Шаг 1: Чтобы найти множители 12 методом деления, нам нужно проверить, какие числа полностью делят 12. Начнем проверку с 1 и дойдем до 9. Нам нужно сделать пометку из тех чисел, которые делят 12 полностью.
• Шаг 2: Числа, которые полностью делят 12, называются его делителями. Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Как мы проверяем и перечисляем все числа до 9, вместе с ним мы автоматически получаем другой парный множитель. Например, начиная с 1, мы пишем 12 ÷ 1 = 12, а 12 ÷ 2 = 6 и так далее. Здесь делитель и частное являются делителями числа. Это означает, что (1, 12) образует первую пару, (2, 6) образует вторую пару, и список продолжается, как показано. Итак, когда мы пишем 1 как множитель 12, мы получаем другой множитель как 12; и поскольку мы пишем 2 как множитель 12, мы получаем 6 как другой множитель. Таким образом, мы получаем все факторы.
• Шаг 3 : После того, как список отмечен, мы получаем все множители 12, начиная с 1, затем уменьшаемся, а затем снова поднимаемся вверх до 12. Это дает нам полный список всех множителей 12, как показано на приведенном выше рисунке.

Следовательно, делители числа 12 могут быть перечислены как 1, 2, 3, 4, 6, 12.

Теперь давайте научимся находить делители числа методом умножения. Это почти то же самое, что и метод деления, с той лишь разницей, что множители пишутся в разных местах.

Нахождение множителей с помощью метода умножения

Чтобы найти множители числа с помощью метода умножения, нам нужно использовать процедуру, аналогичную описанной выше, за исключением нескольких изменений. Давайте изучим этот метод с помощью примера.

Пример: Найдите множители числа 24, используя метод умножения.

Решение: Давайте найдем множители 24 методом умножения, используя следующие шаги.

• Шаг 1: Чтобы найти множители 24 с помощью умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 24, поэтому нам нужно разделить 24 на натуральные числа, начиная с 1, и продолжать до 9.
• Шаг 2: Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Когда мы проверяем и перечисляем все числа до 9, мы автоматически получаем вместе с ним другой парный коэффициент. Например, начиная с 1, мы пишем 1 × 24 = 24 и 2 × 12 = 24 и так далее. Здесь (1, 24) образует первую пару, (2, 12) образует вторую пару, и список продолжается, как показано. Итак, когда мы записываем 1 как множитель 24, мы получаем другой множитель как 24; и поскольку мы пишем 2 как множитель 24, мы получаем 12 как другой множитель. Таким образом, мы получаем все факторы.
• Шаг 3 : После того, как список записан, мы получаем все делители числа 24, начиная с 1 вверх, вниз, а затем снова поднимаемся вверх до 24. Это дает нам полный список всех делителей числа 24 в виде показано на рисунке, приведенном выше.

Следовательно, множители 24 могут быть перечислены как 1, 2, 3, 4, 6, 8, 12 и 24.

Нахождение числа факторов

Мы можем найти количество множителей заданного числа, используя следующие шаги.

• Шаг 1: Произведите разложение заданного числа на простые множители, т. е. представите его как произведение простых чисел.
• Шаг 3: Запишите простую факторизацию в форме экспоненты.
• Шаг 3: Добавьте 1 к каждому показателю степени.
• Шаг 4: Перемножьте все полученные числа. Это произведение дает количество факторов заданного числа.

Пример: Найдите количество делителей числа 108.

Решение: Давайте найдем количество множителей 108, используя шаги, указанные ниже.

• Шаг 1: Разложение числа 108 на простые множители дает нам 108 = 2 × 2 × 3 × 3 × 3
• Шаг 2: После записи простой факторизации в экспоненциальной форме мы получаем 108 = 2 ² × 3 ³
• Шаг 3: После добавления 1 к каждому из показателей степени, 2 и 3, мы получаем (2 + 1) = 3, (3 + 1) = 4.
• Шаг 4: Теперь давайте умножим эти числа: 3 × 4 = 12. Следовательно, число множителей 108 равно 12,9.
  0062

Мы можем проверить это число, записав действительные делители 108, которые равны 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54 и 108. Здесь 108 имеет 12 делителей, следовательно, мы проверили, что 108 имеет 12 делителей.

Факторы чисел

Вот список страниц, объясняющих множители различных чисел.

 

Факторы Примеры

1. Пример 1: Найдите положительные множители числа 64.

   Решение:

   Найдем множители числа 64, используя метод умножения.

   • Чтобы найти множители 64 с помощью умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 64, поэтому нам нужно разделить 64 на натуральные числа, начиная с 1 и продолжая до 9, так что мы получим 1 × 64 = 64 и 2 × 32 = 64, 4 × 16 = 64, 8 × 8 = 64.
   • После того, как список записан, мы получаем все делители числа 64, начиная с 1 вверх, вниз и снова поднимаясь вверх до 64. Это дает нам полный список всех делителей числа 64.
   • Следовательно, положительные множители числа 64 = 1, 2, 4, 8, 16, 32, 64.

2. Пример 2: Какое из следующих утверждений верно?

   а.) Множитель числа может быть больше числа.

   б.) Некоторые числа могут иметь бесконечное число множителей.

   Решение:

   а.) Утверждение «Множитель числа может быть больше числа» ЛОЖЬ. Мы знаем, что множители — это делители числа, при которых в остатке остается 0. Следовательно, они всегда меньше числа. Следовательно, ответ: Ложь

   б.) Утверждение «Некоторые числа могут иметь бесконечное число множителей» ЛОЖЬ. Количество множителей числа конечно. Следовательно, ответ: Ложь.

3. Пример 3: Найдите количество делителей числа 1620.

   Решение:

   • Чтобы найти количество делителей числа 1620, мы сначала проведем его разложение на простые множители. дерево факторов показано ниже
   • Разложение числа 1620 на простые множители = 2 × 2 × 3 × 3 × 3 × 3 × 5. В форме экспоненты это можно выразить как 2 ² × 3 ⁴ × 5 ¹ .
   • Прибавляя 1 к каждому из показателей степени, получаем: 2 + 1 = 3, 4 + 1 = 5, 1 + 1 = 2.
   • Произведение всех этих чисел: 3 × 5 × 2 = 30. Следовательно, число делителей числа 1620 равно 30.
   • Проверим это число, найдя множители 1620. Множители 1620 = 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 81, 90, 108, 135, 162, 180, 270, 324, 405, 540, 810 и 1620. Итак, мы можно увидеть, что 1620 имеет всего 30 множителей.

перейти к слайдуперейти к слайдуперейти к слайду

Воспитайте логических мыслителей и укрепите их уверенность!

Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!

Забронировать бесплатное пробное занятие

Практические вопросы по факторам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о факторах

Что такое факторы в математике?

Коэффициент — это число, на которое данное число делится без остатка. Делители числа могут быть как положительными, так и отрицательными. Факторы любого числа конечны. Например, делители числа 7 равны 1 и 7. Делители числа 8 равны 1, 2, 4 и 8.

Как найти количество делителей числа?

Мы можем найти количество множителей заданного числа, используя следующие шаги. Разберемся в этом на примере и найдем количество множителей 48

• Шаг 1: Разложите заданное число на простые множители. Это будет 48 = 2 × 2 × 2 × 2 × 3
.
• Шаг 3: Запишите простую факторизацию в форме экспоненты. Это можно записать как 2 ⁴ × 3 ¹
• Шаг 3: Добавьте 1 к каждому показателю степени. Показатели степени в данном случае равны 4 и 1. Таким образом, прибавив 1 к каждому показателю степени, мы получим 5 и 2.
• Шаг 4: Перемножьте полученные числа. Это произведение дает количество факторов заданного числа. После умножения 5 × 2 = 10. Это означает, что 48 имеет 10 делителей. Проверим это, перечислив множители числа 48. Множители числа 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48,9.0062

Что такое простая факторизация?

Разложение числа на простые множители — это способ представления числа как произведения его простых множителей. Например, разложение числа 60 на простые множители = 2 × 2 × 3 × 5. Разложение числа на простые множители всегда показывает его простые множители. В данном случае 2, 2, 3 и 5 — это простые множители числа 60. Мы знаем, что простые множители — это те множители, которые являются простыми числами.

Что такое формула факторов?

Формула множителей числа дает общее количество множителей числа. Для числа N, простая факторизация которого равна X ^a × Y ^b , мы получаем общее количество факторов, добавляя 1 к каждому показателю степени, а затем перемножая их вместе. Это выражает формулу числа факторов как (a + 1) × (b + 1), где a и b — показатели степени, полученные после простой факторизации данного числа. Например, давайте найдем общее количество делителей числа 12. Разложение числа 12 на простые множители = 2 × 2 × 3. Это можно записать в виде экспоненты как 2 ² × 3 ¹ . Воспользуемся формулой (a + 1) × (b + 1), где a и b равны 2 и 1 соответственно. После подстановки значений мы получаем (a + 1) × (b + 1) = (2 + 1) × (1 + 1) = 3 × 2 = 6. Это означает, что 12 имеет всего 6 делителей. Это можно проверить, перечислив множители числа 12: 1, 2, 3, 4, 6, 12.

Каковы общие делители чисел 4 и 12?

Делители числа 4 равны 1, 2 и 4. Делители числа 12 равны 1, 2, 3, 4, 6 и 12. Таким образом, можно видеть, что общие делители числа 4 и 12 равны 1, 2 и 4.

Какое число является делителем каждого числа?

1 является делителем каждого числа, потому что 1 полностью делит каждое число.

Что такое простые делители числа?

Простым множителем числа называется множитель, являющийся простым числом. Например, простые множители числа 12 равны 2, 2 и 3, потому что 2 × 2 × 3 = 12. Эти простые множители при умножении вместе дают произведение в виде числа. Простые множители числа можно вычислить с помощью метода факторного дерева или метода деления.

Могут ли коэффициенты быть отрицательными?

Да, делители числа могут быть отрицательными, потому что мы знаем, что произведение двух отрицательных чисел является положительным числом. Например, если мы умножим (-2) × (-3), мы получим 6. Точно так же (-1) × (-6) = 6. Это означает, что -1, -2, -3 и -6 являются отрицательные множители 6. Это показывает, что число может иметь положительные и отрицательные множители. В этом случае положительные факторы 6 могут быть перечислены как 1, 2, 3 и 6; а отрицательные факторы 6 могут быть перечислены как -1, -2, -3 и -6.

Как делить большие числа с помощью длинного деления

Авторы: Марк Зегарелли и

Обновлено: 07-08-2021

Рабочая тетрадь по основам математики и алгебры для чайников с онлайн-практикой

Книга для изучения Купить на Amazon

Чтобы разделить большие числа, используйте длинное деление . В отличие от других операций «Большой четверки», длинное деление движется слева направо. Для каждой цифры в делимое (число, которое вы делите), вы завершаете цикл деления, умножения и вычитания.

В некоторых задачах число в самом низу задачи не равно 0. В этих случаях ответ имеет остаток , , который является остатком, который необходимо учитывать. В этих случаях вы пишете r , а затем любое оставшееся число.

Примеры вопросов

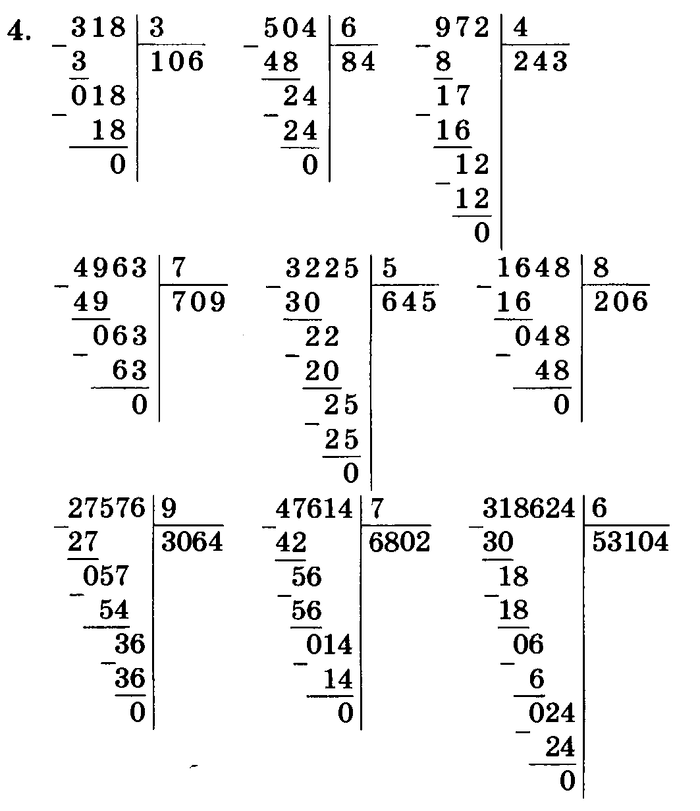
1. Разделить 956/4.

   239. Начните с написания задачи следующим образом:

   Для начала спросите, сколько раз 4 входит в 9, то есть что такое 9/4? Ответ: 2 (с небольшим остатком), поэтому напишите 2 прямо над 9. Теперь умножьте 2 x 4, чтобы получить 8, поместите произведение прямо под 9 и нарисуйте линию под ним:

   Вычтите 9–8, чтобы получить 1. ( Примечание: После вычитания результат должен быть меньше делителя (в этой задаче делитель равен 4). Затем опустите следующее число (5), чтобы получилось новый номер 15.

   Эти шаги составляют один полный цикл. Чтобы выполнить задачу, нужно просто повторить их. Теперь спросите, сколько раз 4 входит в 15, то есть что такое 15/4? Ответ 3 (с небольшим остатком). Поэтому запишите 3 над 5, а затем умножьте 3 x 4, чтобы получить 12. Запишите произведение под 15.

   Вычтите 15–12, чтобы получить 3. Затем запишите следующее число (6), чтобы получить новое число 36.

   Еще один цикл завершен, так что начните следующий цикл, спросив, сколько раз 4 входит в 36, то есть сколько будет 36/4? На этот раз ответ 9. Запишите 9 над 6, умножьте 9 на 4 и поместите это под 36.

   Теперь вычтите 36 – 36 = 0. Поскольку у вас больше нет чисел, которые нужно записывать, вы закончили, и ответ (то есть частное ) является самым верхним числом задачи:

2. Разделить 3042 / 5.

   608 r 2. Начните с написания задачи следующим образом:

   Для начала спросите, сколько раз 5 входит в 3. Ответ 0, потому что 5 не входит в 3, поэтому напишите 0 над 3. Теперь вам нужно задать тот же вопрос, используя первые два разряда делителя: Сколько раз 5 входит в число 30 — то есть чему равно 30/5? Ответ 6, поэтому поместите 6 над 0. Вот как завершить первый цикл:

   Затем спросите, сколько раз 5 переходит в 4. Ответ 0, потому что 5 не входит в 4, поэтому напишите 0 над 4. Теперь запишите следующее число (2), чтобы получилось число 42:

   Спросите, сколько раз 5 входит в число 42, то есть что такое 42/5? Ответ 8 (с небольшим остатком), поэтому завершите цикл следующим образом:

   Поскольку у вас больше нет номеров для ввода, с вами покончено. Ответ (частное) находится в верхней части задачи (можно опустить начальный 0), а остаток — в нижней части задачи. Таким образом, 3 042 / 5 = 608 с остатком 2. Для экономии места запишите этот ответ как 608 r 2.

Практические вопросы

1. Разделить 741/3.

2. Оценка 3245/5.

3. Вычисление 91 390 / 8.