Сложение десятичных дробей: правила и примеры
- Сложение путём перевода в обыкновенные дроби
- Сложение десятичных дробей столбиком
- Сложение десятичной дроби с натуральным числом
- Сложение десятичной дроби с обыкновенной дробью
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.

Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.

- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Пример. Выполнить сложение десятичной дроби 0,28 и обыкновенной дроби .
Решение. Переводим десятичную дробь 0,28 в обыкновенную: . И далее выполняем уже сложение обыкновенных дробей и :
Сложение и вычитание десятичных дробей
Тема: Сложение и вычитание десятичных дробей
Чтобы научиться правильно выполнять сложение десятичных дробей, достаточно выучить правило, состоящее всего из трех слов.
Три слова такие: запятая под запитой. Это самое важное, что следует помнить при сложении десятичных дробей. Складывая десятичные дроби, мы записываем их так, чтобы запятые в слагаемых находились строго одна под другой. Если после запятой в одном слагаемом цифр меньше, чем в другом, можно недостающие цифры дополнить нулями (а можно и не делать этого). В остальном сложение десятичных дробей практически ничем не отличается от сложения натуральных чисел — темы, которую проходили еще в начальной школе.
Запомните!
Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Итак, ещё раз коротко основные правила сложения:
- уравниваем количество знаков после запятой;
- записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом;
- выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
- ставим в ответ запятую под запятыми.

Рассмотрим на примерах, как происходит сложение десятичных дробей.
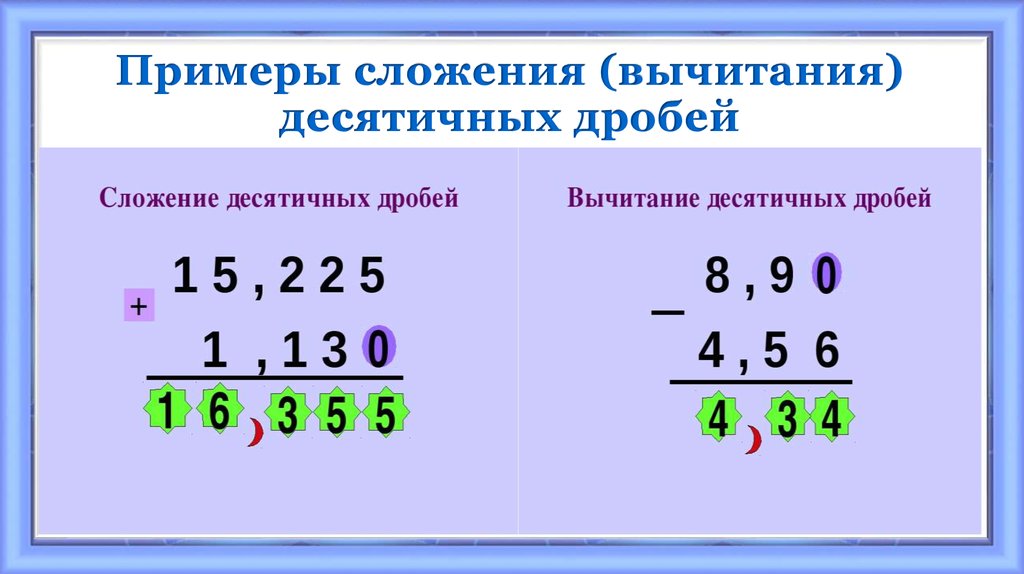
Чтобы сложить 5,7 и 6,8, записываем их запятая под запятой. Затем складываем цифры по разрядам и в полученном ответе сносим запятую все по тому же правилу — запятая под запятой.
При сложении 2,256 и 0,74 числа записываем так, чтобы запятая находилась под запятой. Поскольку во втором числе после запятой два знака, а в первом — три, недостающий один знак в конце второго числа дополняем нулем (но его можно и не писать). После этого складываем числа, не обращая внимания на запятую (то есть к 2256 прибавляем 740). В результате сносим запятую (ровно под запятой слагаемых).
Как обычно, сложение десятичных дробей начинаем с их записи таким образом, чтобы запятая стояла точно под запятой. Первым удобнее записать число, у которого количество цифр после запятой больше. Чтобы уравнять количество знаков после запятой в обоих слагаемых, во втором третьей цифрой после запятой записываем нуль. Складываем 52462 и 4980, не обращая внимания на запятую. В ответе сносим запятую под запятой.
Складываем 52462 и 4980, не обращая внимания на запятую. В ответе сносим запятую под запятой.
Чтобы сложить десятичные дроби, записываем их «запятая под запятой». Складываем 4821 и 3179, не обращая внимания на запятую. После этого сносим запятую под запятой. Поскольку в десятичной дроби после запятой нули на конце не пишут, окончательный ответ 8.
Чтобы к натуральному числу прибавить десятичную дробь, можно в записи натурального числа в конце приписать запятую и столько нулей, сколько нужно (в данном примере — три). Затем складываем 35000 и 3146 и сносим запятую.
Сложение начинаем с записи десятичных дробей по правилу «запятая под запятой». Затем недостающий знак после запятой у числа 8,3 дополняем нулем. Складываем 374 и 830. В ответ сносим запятую под запятой.
Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.
Правило вычитания десятичных дробей
1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!
Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.
При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.
2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.
3) Вычитаем числа, не обращая внимания на запятую.
4) Сносим запятую под запятыми.
Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:
9,7-3,5=6,2.
Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой. Так как у 23,45 после запятой две цифры, а у 1,5 — только одна, дописываем в 1,5 нуль. После этого ведем вычитания, не обращая внимания на запятую. В результат сносим запятую под запятыми:
23,45 — 1,5=21,95.
Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:
63,5-8,921=54,579.
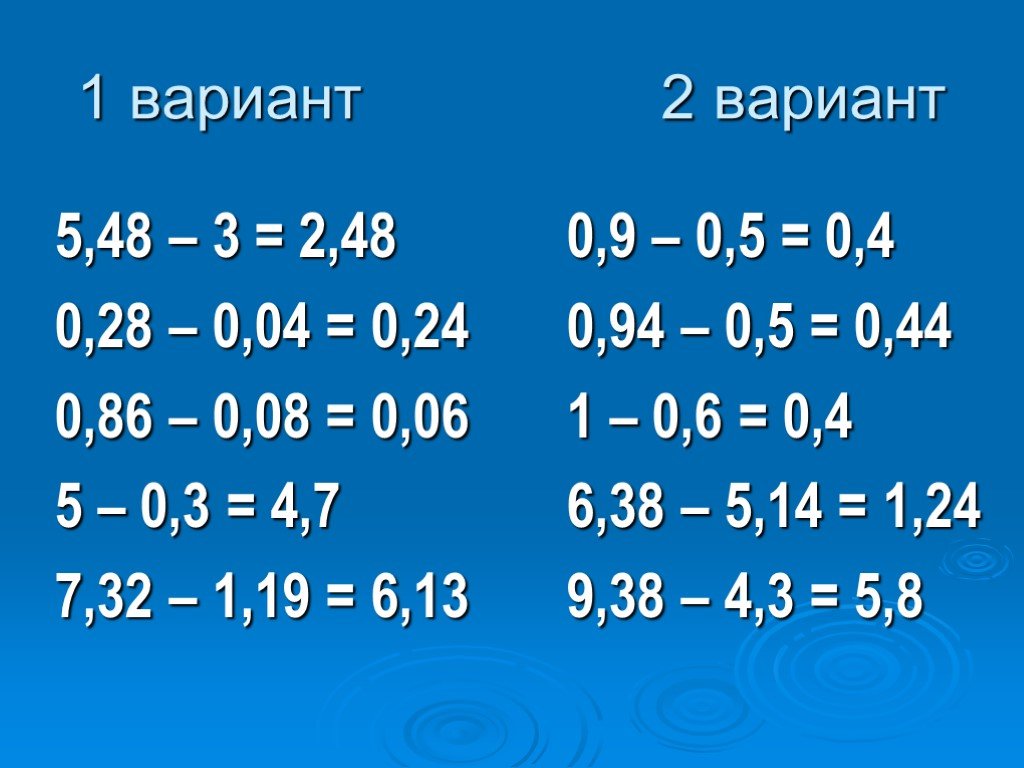
Задания для самостоятельного решения:
1. Вычислите:
а) 10,3 – 8,17; б) 9,432 – 8,32; в) 7,3 + 0,865;
г) 4,1 – 2,74; д) 2,031 – 1,05; е) 3,6 + 0,55
2. Выполните сложение:
1,08 + 5,1 + 0,988 =
3. Решите уравнение:
х +3,72 = 8
4. Вычислите выражение:
12,36 + ((11,31 + 0,03) — 1,38) — 3, 04 =
5. Решите задачу:
В первый день магазин продал 87,5 кг сахара, а во второй – на 9,85 кг больше. Сколько килограммов сахара продал магазин за два дня?
Сложение и вычитание десятичных дробей – методы, примеры
Сложение и вычитание десятичных дробей выполняется так же, как сложение и вычитание целых чисел с учетом того, что десятичная точка должна быть на месте. Длину десятичных чисел можно регулировать, добавляя или удаляя нули из десятичной части. Давайте узнаем больше о сложении и вычитании десятичных дробей в этой статье.
Длину десятичных чисел можно регулировать, добавляя или удаляя нули из десятичной части. Давайте узнаем больше о сложении и вычитании десятичных дробей в этой статье.
| 1. | Что такое сложение и вычитание десятичных дробей? |
| 2. | Как складывать и вычитать десятичные дроби с целыми числами? |
| 3. | Часто задаваемые вопросы о десятичном сложении и вычитании |
Что такое сложение и вычитание десятичных дробей?
Сложение и вычитание десятичных дробей включает обычные правила сложения и вычитания. Единственные моменты, о которых следует позаботиться, — это десятичные знаки после запятой. Числа должны быть записаны в столбцах в соответствии с их разрядами до и после запятой. Таблица десятичных разрядов показывает, что разряды до десятичной точки начинаются с десятков, сотен и т.
Сложение десятичных знаков
Сложение десятичных знаков выполняется, начиная с правой стороны, а затем мы двигаемся влево, добавляя каждый столбец. Например, добавим 12,5 + 14,9, выполнив следующие действия.
- Шаг 1: Напишите числа одно под другим так, чтобы они были выровнены в соответствии со своими разрядными значениями, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь сложите десятичные числа, чтобы получить сумму. В данном случае 12,5 + 14,9= 27,4
Теперь давайте разберемся с вычитанием десятичных знаков в следующем разделе.
Вычитание десятичных дробей
Вычитание десятичных дробей выполняется так же, как вычитание целых чисел. Нам просто нужно правильно записать числа в соответствии с их разрядными значениями. Давайте разберемся в этом с помощью примера, приведенного ниже.
Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: Вычесть указанные десятичные дроби: 15,8 — 2,7
Решение: Вычтем эти десятичные дроби, используя следующие шаги.
- Шаг 1: Напишите числа одно под другим так, чтобы большее число было сверху, а меньшее число было написано под ним.
- Шаг 2: Теперь вычтите десятичные числа, начиная со столбца десятых, переходя к столбцу единиц, а затем к столбцу десятков. Скопируйте десятичную дробь, как она есть. В этом случае 15,8 — 2,7 = 13,1
Сложение и вычитание в отличие от десятичных дробей
‘В отличие от десятичных дробей’ — это те десятичные числа, которые имеют разное количество цифр после запятой. Например, 3,45 и 7,831 «не похожи на десятичные числа», потому что 3,45 имеет два числа после запятой, а 7,831 — три числа после запятой. Другими словами, в отличие от десятичных дробей говорят, что они имеют разную длину.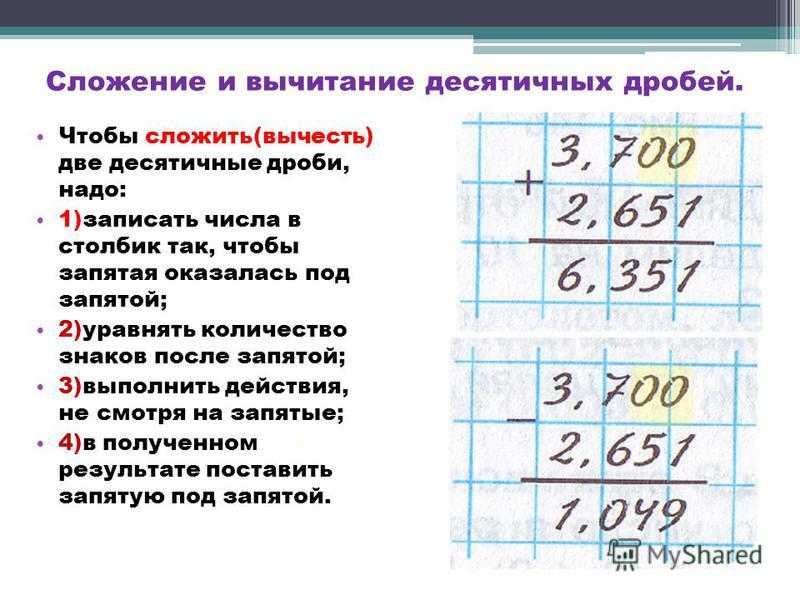 Операции сложения и вычитания удобно выполнять даже с такими непохожими десятичными дробями. Нам просто нужно преобразовать «непохожие десятичные числа» в «подобные десятичные числа», написав нули в тех местах, где длина десятичных чисел не одинакова. Таким образом, десятичные цифры в каждом из чисел становятся равными, и числа легче складывать или вычитать. Давайте разберемся в этом с помощью следующего примера.
Операции сложения и вычитания удобно выполнять даже с такими непохожими десятичными дробями. Нам просто нужно преобразовать «непохожие десятичные числа» в «подобные десятичные числа», написав нули в тех местах, где длина десятичных чисел не одинакова. Таким образом, десятичные цифры в каждом из чисел становятся равными, и числа легче складывать или вычитать. Давайте разберемся в этом с помощью следующего примера.
Пример: Сложите десятичные числа 24, 32,1, 0,08, 0,5 и 4,003
Решение: Сложим эти числа, выполнив следующие действия.
- Шаг 1: Здесь каждое из чисел должно иметь одинаковое количество десятичных цифр.
- Шаг 2: Для этого перепишем числа следующим образом: 24.000, 32.100, 0.080, 0.500 и 4.003. Следовательно, сумма данных десятичных чисел равна 60,683 .
Как складывать и вычитать десятичные дроби с целыми числами?
При сложении или вычитании десятичного и целого числа целое число преобразуется в десятичное число. Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, целое число 5 записывается в десятичной форме как 5,0. Давайте разберемся в этом с помощью следующих примеров.
Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, целое число 5 записывается в десятичной форме как 5,0. Давайте разберемся в этом с помощью следующих примеров.
Пример: Добавьте 15 + 12,56
- Шаг 1: Обратитесь к цифре, приведенной выше, и поставьте десятичную запятую после 15 и напишите два нуля после нее, чтобы оба числа стали как десятичные дроби.
- Шаг 2: Теперь сложите десятичные числа и найдите сумму, используя обычные правила сложения. Следовательно, 15 + 12,56 = 27,56
Давайте поймем это с помощью вычитания.
Пример: Вычесть 6 — 2,25
- Шаг 1: Обратитесь к цифре, приведенной выше, и поставьте десятичную запятую после 6 и напишите два нуля после нее, чтобы оба числа стали как десятичные дроби.
- Шаг 2: Теперь вычтите десятичные числа и найдите разницу, используя обычные правила вычитания.
 Следовательно, 6 — 2,25 = 3,75
Следовательно, 6 — 2,25 = 3,75
Важные моменты при сложении и вычитании десятичных знаков
- Значение десятичного числа не меняется при размещении нуля после десятичных цифр. Например, 5 можно записать как 5,00 9.0046
- Несмотря на то, что мера времени и угла представлена в десятичном формате, их нельзя складывать или вычитать как десятичные числа.
☛ Похожие темы
- Сложение и вычитание десятичных дробей
- Сложение и вычитание десятичных дробей 6 класс
- Сложение и вычитание десятичных дробей 5 класс
- Деление десятичных дробей
- Умножение десятичных дробей
Примеры десятичного сложения и вычитания
Пример 1: Добавьте 0,2 + 0,22 + 0,222 + 0,2222, используя правила десятичного сложения и вычитания.
Решение:
Заданные десятичные числа будут преобразованы в одинаковые десятичные числа путем размещения необходимого количества нулей после десятичных знаков, так что каждое число имеет одинаковое количество десятичных знаков.
 Их можно записать следующим образом.
Их можно записать следующим образом.∴ Сумма данных десятичных знаков равна 0,8642
Пример 2: Найдите разницу между 7847 и 78,47, используя концепцию сложения и вычитания десятичных знаков.
Решение:
Число 7847 записывается в десятичной форме как 7847,00. Теперь вычитание можно выполнить следующим образом.
Следовательно, 7847 — 78,47 = 7768,53
Пример 3: Запишите истину или ложь относительно десятичного сложения и вычитания.
а.) 20 + 12,17 = 32,17
а.) 10 + 69,32 = 69,42
Решение:
а.)
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по сложению и вычитанию десятичных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о десятичном сложении и вычитании
Как складывать и вычитать десятичные дроби?
Сложение и вычитание десятичных дробей выполняется с использованием обычных правил сложения и вычитания. Единственное, что нужно иметь в виду, это количество цифр после запятой и то, что десятичная точка должна быть правильно размещена в сумме или разнице. Числа должны быть записаны в столбцы в соответствии с их разрядами до и после запятой, а затем они сложены или вычтены.
Единственное, что нужно иметь в виду, это количество цифр после запятой и то, что десятичная точка должна быть правильно размещена в сумме или разнице. Числа должны быть записаны в столбцы в соответствии с их разрядами до и после запятой, а затем они сложены или вычтены.
Каково правило сложения и вычитания десятичных дробей?
Правило сложения и вычитания десятичных знаков связано с десятичной точкой. Например, чтобы сложить 56,12 + 10,14, нам нужно выровнять эти числа одно под другим так, чтобы десятичная точка встала на место и все числа были записаны в соответствии со значениями разряда. В результате получится 66,26. В случае, если они не похожи на десятичные числа, нам нужно преобразовать их в одинаковые десятичные числа, написав соответствующее количество нулей после запятой, чтобы десятичные разряды стали равными. Например, 34,25 + 12,986 можно записать как 34,250 + 12,986 и сумма будет 34,250 + 12,986 = 47,236
Как складывать и вычитать десятичные дроби с целыми числами?
Чтобы складывать и вычитать десятичные дроби с целыми числами, нам нужно преобразовать целое число в десятичное число. Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, если нам нужно сложить 8 + 4,321, то мы можем записать целое число 8 в десятичной форме как 8,000, а затем прибавить его к 4,321. После этого числа можно сложить и записать как 8.000 + 4.321 = 12.321
Это делается путем размещения десятичной дроби после целого числа, а затем записи необходимого количества нулей после запятой. Например, если нам нужно сложить 8 + 4,321, то мы можем записать целое число 8 в десятичной форме как 8,000, а затем прибавить его к 4,321. После этого числа можно сложить и записать как 8.000 + 4.321 = 12.321
Как складывать десятичные числа?
Для сложения любых двух десятичных чисел мы используем следующие шаги. Давайте разберемся в этом на примере. Например, добавим 23,12 + 4,23
- Шаг 1: Напишите числа одно под другим так, чтобы они были выровнены в соответствии со своими разрядными значениями, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь сложите десятичные числа, чтобы получить сумму. В этом случае будет 23,12 + 4,23 = 27,35
Как вычитать десятичные числа?
Чтобы вычесть любые два десятичных числа, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте вычтем 44,32 — 3,6
Например, давайте вычтем 44,32 — 3,6
- Шаг 1: Запишите числа одно под другим так, чтобы они были выровнены в соответствии со своими разрядными значениями, а десятичная точка располагалась одна под другой.
- Шаг 2: Теперь вычтите десятичные числа, чтобы получить разницу. В этом случае будет 44,32 — 03,60 = 40,72
Как сложить десятичное число и целое число?
Чтобы прибавить десятичное число к целому числу, нужно преобразовать целое число в десятичное. Например, добавим 5 и 3,236. Здесь мы меняем 5 на 5.000 и получаем 5.000 + 3.326 = 8.326
Как умножить два десятичных знака?
Умножение десятичных дробей на целые числа аналогично умножению целых чисел. Разница только в расположении десятичной точки. Для умножения десятичных дробей на целые числа можно выполнить следующие шаги:
- Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.

- Шаг 2: После умножения подсчитайте количество знаков после запятой в данных десятичных числах. Предположим, что множимое имеет 2 числа после запятой, а множитель имеет 1 число после запятой, тогда мы сложим эти 2 + 1 = 3. Итак, мы поместим десятичную дробь в произведении через 3 знака справа. Например, 0,04 × 0,2 = 0,008
Как разделить десятичную дробь на другую десятичную?
Чтобы разделить десятичное число на десятичное число, нам нужно преобразовать делитель в целое число, а затем продолжить деление. Например, если нам нужно разделить 13,8 ÷ 0,6, мы будем использовать следующие шаги.
- Шаг 1: Делимое равно 13,8, а делитель 0,6. Нам нужно изменить делитель на целое число, и поэтому мы умножим его на 10, чтобы десятичная точка сместилась вправо, и оно стало целым числом. Это означает, что 0,6 × 10 = 6
- Шаг 2: Нам нужно обращаться с делимым так же, как мы обращались с делителем.
 Значит, делимое тоже умножим на 10. Это означает, что будет 13,8 × 10 = 138. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом. Следовательно, 138 ÷ 6 = 23, .
Значит, делимое тоже умножим на 10. Это означает, что будет 13,8 × 10 = 138. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом. Следовательно, 138 ÷ 6 = 23, .
Скачать БЕСПЛАТНЫЕ учебные материалы
Сложение и вычитание десятичных дробей Рабочий лист
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробейСложение и вычитание десятичных дробей
|



 Следовательно, 6 — 2,25 = 3,75
Следовательно, 6 — 2,25 = 3,75 Их можно записать следующим образом.
Их можно записать следующим образом.
 Значит, делимое тоже умножим на 10. Это означает, что будет 13,8 × 10 = 138. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом. Следовательно, 138 ÷ 6 = 23,
Значит, делимое тоже умножим на 10. Это означает, что будет 13,8 × 10 = 138. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом. Следовательно, 138 ÷ 6 = 23,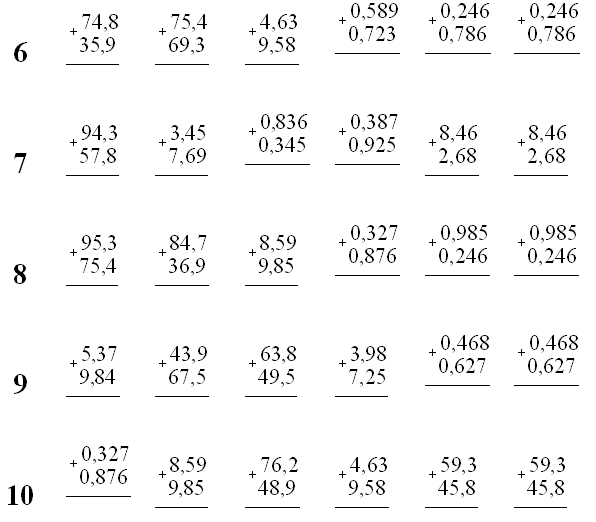 Для десятичных дробей мы выстраиваем
десятичных знаков так, чтобы целые части числа совпадали, а десятичные части
расстановка. Затем добавьте каждый.
Для десятичных дробей мы выстраиваем
десятичных знаков так, чтобы целые части числа совпадали, а десятичные части
расстановка. Затем добавьте каждый. 29
29 В частности, выполните следующие действия:
В частности, выполните следующие действия:  00942 — 12.0087
00942 — 12.0087