Контрольная работа № 8 «Умножение многозначных чисел» 3 класс. ОС «Перспектива». Математика Л.Г. Петерсон
Главная / Начальные классы / Математика
Скачать
14.59 КБ, 595532.docx Автор: Никулина Ирина Витальевна, 30 Мар 2015
Контрольная работа включает в себя примеры на умножение многозначных чисел, задачи на нахождение цены и геометрическую, решение примера на много действий и перевод именованных единиц. Контрольной работы в сборнике на эту тему нет.
Автор: Никулина Ирина Витальевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Контрольная работа № 8 «Умножение многозначных чисел» 3 класс. ОС «Перспектива». Математика Л.Г. Петерсон | Никулина Ирина Витальевна | 30 Мар 2015 |
| документ | Контрольная работа по математике за первое полугодие. 4 класс. Программа «Перспектива» Л.Г. Петерсон. | Афанасьева Наталья Владимировна | 30 Мар 2015 |
| документ | Рабочая программа по математике 3 класс УМК «Перспектива» Петерсон Л.Г. | Попова Елена Васильевна | 11 Апр 2015 |
| документ | Контрольная работа по математике,4 класс по теме «Умножение и деление многозначных чисел на однозначное» | Ершова Татьяна Антоновна | 21 Дек 2015 |
| документ | Урок математики по учебнику Л. Г. Петерсон «Математика», 1-й класс (программа «Перспектива»). | Кукушкина Виктория Александровна | 25 Авг 2015 |
| документ | Урок математики 1 класс по теме «Число и цифра 7» УМК «Перспектива» автор учебника Л.Г. Петерсон | Макарова Елена Владимировна | 30 Мар 2015 |
| документ | Контрольная работа за 3 четверть 3 класс Программа «Школа 2100″Петерсон | Кучина Ирина Васильевна | 5 Апр 2015 |
| документ | Контрольная работа по математике . 3 класс. 1 четверть. Программа «Школа -2100» Петерсон Л. Г. | Кучина Ирина Васильевна | 30 Мар 2015 |
| разное | Урок по математике «Деление круглых чисел». 2 класс. «Школа 2000…» (автор учебника Л.Г. Петерсон) | Калаева Светлана Сосланбековна | 30 Мар 2015 |
| разное | Программа по математике Петерсон Л.Г. 1 класс » Перспектива» | Андрева Татьяна Петровна | 30 Мар 2015 |
| разное | Программа по математике Петерсон Л.Г. 1 класс » Перспектива» | Андрева Татьяна Петровна | 30 Мар 2015 |
| разное | Календарно-тематическое планирование по математике Петерсон Л. Г. 1 класс » Перспектива» | Андрева Татьяна Петровна | 30 Мар 2015 |
| документ | Мохова Ольга Игорьевна | 30 Мар 2015 | |
| документ | Контрольная работа «Сложение и вычитание многозначных чисел» | Третьякова Лариса Фёдоровна | 30 Мар 2015 |
| документ | Итоговая контрольная работа по математике за 2 класс по УМК «Перспектива», учебник Л. Г. Петерсон | Передрий Ольга Геннадьевна | 30 Мар 2015 |
| разное | Урок математики по теме:»Площадь прямоугольного треугольника» (4 класс, Петерсон Л. Г.) | Комракова Ирина Фёдоровна | 30 Мар 2015 |
| документ | «Прямой угол» 2 класс (Петерсон Л.Г) | Гришенкова Лариса Николаевна | 30 Июн 2015 |
| документ | Контрольная работа за вторую четверть. 2 класс. Петерсон Л.Г. | Афанасьева Наталья Владимировна | 27 Фев 2016 |
| документ | 1. РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ УМК «ПЕРСПЕКТИВА Л.Г. Петерсон 4 класс. | КРАВЧЕНКО ЕЛЕНА БОРИСОВНА | 30 Мар 2015 |
| документ | контрольная работа по математике,2 класс 4 четверть,Л. Г. Петерсон | Иванова Юлия Сергеевна | 8 Апр 2015 |
| презентация, документ | математика 3 класс «Умножение и деление многозначных чисел на однозначное» | Подолинская Ольга Николаевна | 7 Апр 2015 |
| документ | Контрольная работа № 3 УМК «Перспектива» 2 класс | Пашкова Галина Васильевна | 16 Дек 2015 |
| презентация | Презентация к уроку математики по теме «Умножение многозначных чисел на однозначное.» 3 класс. | Долгова Нина Николаевна | 30 Мар 2015 |
| разное | Презентация к уроку, дистанционному занятию по математике 3-4 класс «Письменное умножение многозначных чисел на однозначное» | Марабаева Лариса Атагулыевна | 31 Мар 2015 |
| документ | Контрольная работа по теме «Умножение» (3 класс) | Колегаева Ольга Владимировна | 4 Июл 2015 |
| документ | Итоговая контрольная работа по математике 3 класс ОС «Школа 2100» | Пешехонова Ольга Павловна | 30 Мар 2015 |
| документ | Контрольная работа по математике за 1 четверть. 3 класс ОС «Школа 2100» | Шимон Светлана Владимировна | 19 Окт 2015 |
| разное | Презентация к уроку «Умножение многозначных чисел с нулями» 4 класс | Кокоулина Виолетта Викторовна | 30 Мар 2015 |
| документ | Тематические контрольные работы по математике № 3, № 4, № 5, № 6 ( программа Л.Г. Петерсон, 2 класс). Итоговая контрольная работа по математике за II четверть. | Калиниченко Ольга Викторовна | 5 Апр 2015 |
| документ | Контрольная работа по математике по теме «Сложение и вычитание многозначных чисел». 4 класс 2 четверть УМК «Школа России» | Серова Екатерина Юрьевна | 6 Дек 2015 |
| разное | Белокопытова Марина Николаевна | 30 Мар 2015 | |
| разное | Рабочая программа по математике для 3 класса УМК «Школа 2000» Л.Г. Петерсон | Калаева Светлана Сосланбековна | 30 Мар 2015 |
| презентация, документ | Конспект урока математики в 3 классе по учебнику Л.Г. Петерсон «Свойства объединения множеств» | Черкасова Ольга Александровна | 31 Мар 2015 |
| разное | Рабочая программа и календарно-тематическое планирование уроков математики в 3 классе по программе «Школа 2000. ..» автора Петерсон Л.Г. | Елисеева Наталья Павловна | 15 Окт 2015 |
| презентация, документ | Открытый урок по математике в 1 классе «Сравнение выражений» по учебнику Л.Г. Петерсон «Математика. 1 класс» | Аверьянова Галина Юрьевна | 31 Мар 2015 |
| документ | Контрольная работа по математике за 3 четверть во 2 классе автор учебника Л.Г. Петерсон | Бронникова Ольга Геннадьевна | 30 Мар 2015 |
| документ | РАБОЧАЯ ПРОГРАММА по математике для 4 класса. УМК «Перспектива» (Петерсон Л.Г.) | Бородинова Татьяна Владимировна | 22 Дек 2015 |
| документ | контрольная работа по математике по теме «Табличное умножение и деление» 2 класс программа «Перспектива» | Прелова Елена Анатольевна | 6 Дек 2015 |
| презентация | Презентация к уроку математики. Л.Г. Петерсон «Умножение и деление на 10, 100» (продолжение) | Усатова Татьяна Фёдоровна | 30 Мар 2015 |
| документ | Урок математики. Л.Г. Петерсон «Умножение и деление на 10,100» (продолжение) | Усатова Татьяна Фёдоровна | 30 Мар 2015 |
Конспект урока по математике в 6 классе «Умножение многозначных чисел на однозначное число»
ГКСОУ «Специальная (коррекционная) общеобразовательная школа-интернат VIII вида г. Камешково»
Урок математики в 6 классе
«Умножение многозначных чисел на однозначное число».
Учитель математики
Каревская Лариса Александровна
2014 год
Тема урока: «Умножение многозначных чисел на однозначное число».
Цель урока: закрепление навыков умножения многозначных чисел, содержащих в некоторых разрядах 0, на однозначное число в ходе решения примеров и задач.
Задачи урока:
1)образовательная: повторить разряды числа; отрабатывать навык увеличения числа в несколько раз; закрепить умение решать составные задачи; повторить разностное сравнение чисел.
2)коррекционно-развивающая: развивать произвольное внимание учащихся при выполнении упражнения на отбор нужных чисел; развивать умение сравнивать числа в ходе записи их в порядке возрастания;
3) воспитательная: воспитывать у учащихся трудолюбие, самостоятельность при выполнении заданий.
Оборудование: учебники «Математика» для 6 класса специальных (коррекционных) образовательных учреждений VIII вида (авторы Г.М. Капустина и М.Н.Перова).
Ход урока.
I.Организационный момент.
Приветствие класса, доклад дежурного.
II.Устные упражнения.
1).На сколько 15>10? 21300? 120
Каким действием отвечают на этот вопрос?
2).Как называются разряды числа класса единиц, например, числа 348? На каком месте справа пишутся единицы? Десятки? Сотни?
Сообщение темы урока и задач урока.
III.Закрепление учебного материала.
-Откройте учебник на стр. 149.
№ 566 (1,2,3) – коллективная работа (задание 1 выполняет у доски 1 ученик задания 2,3 выполняет у доски 2 ученик).
Множители: 1290, 1030, 3004, 1620, 1090, 2005, 1540, 1070. 1)Выпишите множители, в которых разряды единиц обозначены 0, и увеличьте их в 6 раз.
2) Выпишите множители, в которых разряды единиц и сотен обозначены 0, и увеличьте их в 7 раз.
3) Выпишите множители, в которых разряды десятков и сотен обозначены 0, и увеличьте их в 3 раза.
Задача № 559 – коллективное решение (ученик у доски).
В садовом питомнике 1300 саженцев вишен, а саженцев яблонь в 4 раза больше. На сколько больше в питомнике саженцев яблонь, чем саженцев вишен?
Физкультпауза.
Упражнения для плечевого пояса.
Упражнения для пальцев рук.
Упражнения для глаз.
IV.Самостоятельная работа учащихся.
I вариант.
(для сильной группы)
1.Общее задание для обеих групп
№ 565
Увеличьте в 5 раз числа 1600, 1490, 1800, 1200, 1090, 1730, 1583. Запишите полученные ответы по порядку, начиная с наименьшего.
2.Задача № 561.
В заповеднике живут 630 лосей, кабанов в 3 раза больше, чем лосей, а косуль 415.
Сколько всего лосей, кабанов и косуль живёт в заповеднике?
3.Примеры № 571 (1 ст.)
1428∙4 -4843
1264∙7-959
1217∙8-8827
1016∙9-25
II вариант
1.Общее задание для обеих групп
№ 565
Увеличьте в 5 раз числа 1600, 1490, 1800, 1200, 1090, 1730, 1583. Запишите полученные ответы по порядку, начиная с наименьшего.
2.Задача № 556.
В лесопитомнике вырастили 1400 саженцев сосны, саженцев ели в 6 раз больше. Сколько саженцев вырастили в лесопитомнике?
3.Примеры № 563 (4 ст.)
1200 ∙ 8 2306 ∙ 4
3087 ∙ 3 1450 ∙ 5
Тетради сдать на проверку.
V.Задание на дом: с.149 примеры № 563 (1,2 ст.)
VI. Итог урока.
Самоанализ урока математики в 6 классе.
(учитель Каревская Л.А.)
В 6 классе обучается 11 учащихся. Они делятся на 2 группы по возможностям обучения. Учащиеся 1-й группы быстро решают, умеют мыслить, хорошо и с удовольствием работают самостоятельно, умеют решать разные виды задач (5 чел.
). Учащиеся 2-й группы решают медленнее, чаще делают ошибки в вычислениях. Эти ученики могут затрудняться в записи условия и в решении задач. Им требуется иногда помощь учителя. (6 чел.).
3-й группы в этом классе нет. Класс в целом хорошего уровня подготовленности, но есть большие проблемы в межличностных отношениях детей. Часты конфликты между учащимися во внеурочное время. Класс не очень дружный.
Данный урок в изучаемой теме «Умножение многозначных чисел на 1-значное число и круглые десятки» девятый по счету (из 14 уроков). Тип урока – урок закрепления умений и навыков.
Методы ведения урока: словесный (беседа) и практический.
Все учащиеся 6 класса уже научились выполнять письменное умножение чисел, содержащих нули в отдельных разрядах, хотя ещё не все делают это безошибочно. Поэтому целью урока было закрепление навыка умножения многозначных чисел, содержащих нули, на 1-значное число в ходе решения примеров и задач.
В течение урока решались 3 вида задач: 1)образовательные: повторить разряда чисел, умение выполнять увеличение числа в несколько раз и разностное сравнение чисел, умение решать составные задачи; 2) коррекционно-развивающие: развитие произвольного внимания уч-ся при выполнении задания на отбор нужных множителей; умения сравнивать числа в ходе расположения их в порядке возрастания; 3) воспитательные – воспитание трудолюбия и самостоятельности.
Урок содержал следующие этапы:
I Организационный момент.
II Устные упражнения.
III Закрепление учебного материала.
IV Самостоятельная работа уч-ся.
V Домашнее задание.
VI Подведение итогов урока.
Устные упражнения были направлены на актуализацию знаний и умений учащихся и содержали задания на разностное сравнение чисел и повторение разрядов числа.
На этапе закрепления учебного материала проводилась коллективная работа по решению примеров на увеличение чисел в несколько раз, сопровождающаяся отбором нужных множителей, имеющих 0 в нужном разряде, и решение составной задачи на разностное сравнение чисел с использованием учебника.
На уроке использовались методы:
-словесные – беседа для актуализации знаний и при установлении контакта учителя с учащимися;
—практические: упражнения (примеры и задачи).
Формы обучения: коллективная и самостоятельная работы.
Каждый этап урока был направлен на достижение цели урока и решение поставленных задач. В ходе коллективной работы к доске выходили ученики, у которых встречались трудности в решении примеров на умножение чисел с нулями в некоторых разрядах. С помощью учителя и других уч-ся класса они преодолевали эти трудности. Учащиеся школ VIII вида часто забывают, каким действием следует выполнять разностное сравнение чисел.
Поэтому устные упражнения и разбор задачи помогли им это вспомнить. Физкультпауза, проведенная перед самостоятельной работой, помогла учащимся расслабиться и снять напряжение в руках, напряжение глаз, немного отдохнуть.
Организованная на уроке самостоятельная работа позволяет учителю увидеть, как учащиеся 6 класса усваивают данную тему, умеют ли самостоятельно решать задачи. Дифференцированные задания I и II вариантов позволили ученикам работать на доступном им уровне, создают ситуацию успеха и тем самым повышают мотивацию учения, что чрезвычайно важно для детей с ОВЗ. Если 1-е задание (решение примеров на увеличение чисел в несколько раз с последующей записью ответов в порядке возрастания) было общим для обоих вариантов, то два следующих задания были дифференцированы для группы сильных учащихся и более слабой группы. В I варианте (для сильной группы) долее шла задача на нахождение суммы 3-х слагаемых, а во II варианте (слабее группа) была задача стандартная – на вычисление суммы 2-х слагаемых.
В задание № 3 сильным ученикам были предложены примеры в 2 действия, а II варианту – примеры в 1 действие.
Так что объемы выполняемых заданий в этих вариантах тоже были различны. Т.к. уч-ся 2-й группы решали медленнее. Задание на дом тоже полностью соответствует теме урока – это 2 столбика примеров на умножение чисел с нулями в отдельных разрядах.
В течение всего урока царила атмосфера доброжелательности и спокойствия. Учено-познавательная работа была организована через фронтальную индивидуальную, дифференцированную работу. Такая организация позволила включить каждого учащегося в активную деятельность по достижению цели. При выполнении самостоятельной работы осуществлялся самоконтроль.
Учащиеся были организованы и активны во время урока, заинтересованы учебной работой.
Общие результаты урока: план урока выполнен, на уроке реализовывались образовательные, коррекционно-развивающие и воспитательные задачи.
Урок был эффективный. Цель урока достигнута.
Стратегии обучения многозначному умножению
3,8 К акции
Common Core требует, чтобы мы обучали студентов стратегиям, прежде чем знакомить их с традиционными алгоритмами. Когда дело доходит до обучения многозначному умножению, учителя обычно сосредотачиваются исключительно на методе частичных произведений и забывают обо всем остальном. Вместо этого я предпочитаю сначала строить обучение своих студентов, чтобы они были готовы как к частичным продуктам, так и к традиционному алгоритму с более конкретными методами.
Важно, чтобы мы обучали студентов так, как они учатся лучше всего. Один из методов построения лесов состоит в том, чтобы начинать все понятия с конкретного, а затем переходить к более абстрактному. Я рассказываю об этом в своем посте «Преподавание математики, чтобы ученики поняли». В этом случае, когда я обучаю своих студентов умножению многозначных чисел, я сначала начинаю с модели площади, затем работаю над блочной моделью, ввожу свойство дистрибутивности и затем перехожу к методу частичных произведений.
В зависимости от вашего уровня подготовки и стандартов вы можете преподавать традиционный алгоритм позже. Это позволяет использовать строительные леса, а не спасать студентов позже.
Модель площади как стратегия многозначного умножения
Когда я знакомлю своих учащихся с моделью области, я сначала напоминаю им, как эта модель выглядит с помощью основных чисел умножения, таких как 7 x 8. Я даю учащимся основу -десять блоков и пусть они создают массив. Затем я прошу их «просто попробовать» создать модель с большим числом, например 27 x 4. Затем, в зависимости от того, как получится, мы создадим модель. Я либо смоделирую это, либо направлю их. Я напоминаю ученикам о разрядности, и вместе мы сначала создаем стороны нашего массива. Например, в задаче 27 x 4 мы создаем два десятка и семь единиц, используя наши базовые десять блоков с одной стороны, и четыре единицы с другой.
Далее нам нужно заполнить пробел, чтобы создать массив. Я утверждаю, что мы могли бы сделать это с реальным блоком с основанием 10, но это заняло бы у нас много времени.
Вместо этого было бы лучше использовать большие, которые подходят. Это важный шаг, потому что позже он понадобится им, когда они доберутся до двузначных чисел и с пониманием деления. После того, как все заполнено, мы подсчитываем общее количество блоков для этого раздела и суммируем их, чтобы получить окончательный ответ. Вы можете увидеть это в приведенных ниже якорных диаграммах, найденных в моем уроке по математике многозначного умножения в четвертом классе (или найденном на TpT здесь).
Использование площадной модели с двузначными числами для двузначных чисел по сути то же самое, за исключением того, что площадная модель немного больше. (Я не рекомендую переходить к модели 2 на 2 цифры до тех пор, пока вы не попрактикуетесь со всеми многозначными числами по 1 цифре. Этот пост предназначен для того, чтобы помочь всем нуждам в многозначном умножении.) Эта модель области обычно включает в себя более десятков и сотен.
Блочная модель как стратегия умножения нескольких цифр
Блочная модель идеально соответствует модели площади!
Как видно на изображении ниже, я обычно сначала создаю модель области, а затем рисую прямоугольники вокруг нее, чтобы показать своим ученикам взаимосвязь между ними.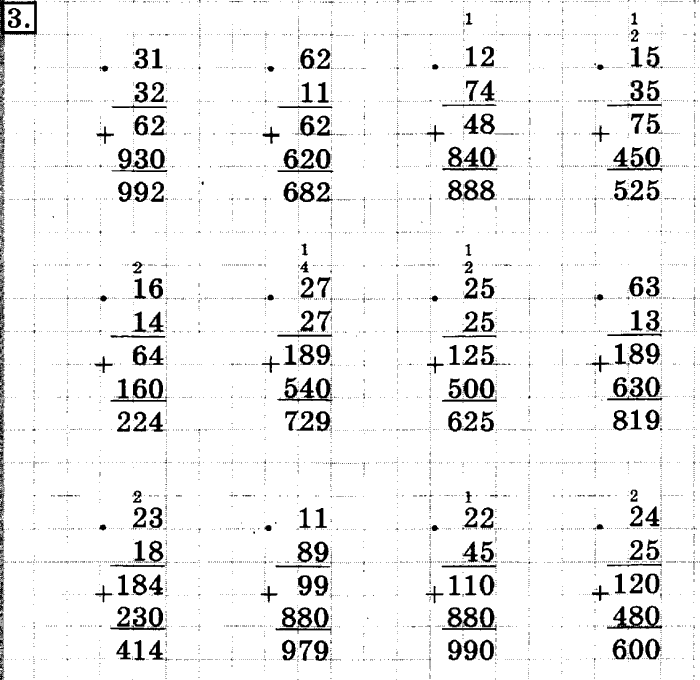
Вместо обычных манипуляций (конкретных) мы теперь переходим к рисованию наших моделей. На самом деле, на моем математическом семинаре и в моем классе я часто заставляю своих учеников рисовать символы блоков с основанием десять после того, как они создали модель области, поэтому переход еще более приятный.
Сейчас студенты находятся на полуконкретном или репрезентативном этапе. Они рисуют квадраты и помещают числа за пределы прямоугольника, чтобы определить ответы для каждого квадрата путем умножения.
Блочная модель ничем не отличается, за исключением того, что теперь они физически не манипулируют блоками с основанием десять. Это прекрасное время, чтобы упомянуть о декомпозиции, потому что это то, что вы будете часто упоминать как в дистрибутивном свойстве, так и позже в других понятиях, таких как площадь.
Когда я говорю о разложении, я люблю напоминать своим ученикам, что на самом деле это ничем не отличается от того, что они делали, когда разбивали числа в развернутую форму.
Когда учащиеся работают над двузначными числами с помощью двузначных чисел, теперь они работают с 4-квадратом. Как и прежде, они только умножают блоки в виде сетки, а затем складывают их. См. диаграммы ниже для более подробного объяснения.
Распределительная модель как стратегия многозначного умножения
По какой-то причине учителя не любят заниматься распределительным свойством, и/или ученики боятся его. Но, если вы проделали свой путь, используя предыдущие методы, эта стратегия не так страшна, как кажется.
Поскольку мы только что говорили о разложении чисел в предыдущей стратегии, учащиеся теперь должны знать, что они могут взять большее число и разбить его на меньшие числа. Я даю им свободу выбора, как они разбивают это. Затем я даю им коробки, чтобы разбить его и размножить!
В нижней части этой диаграммы свойств распределения (выше) вы можете видеть, что я перевернул коробку боком и использовал цветные ручки. Я сделал это намеренно, прежде чем перейти к частичным продуктам.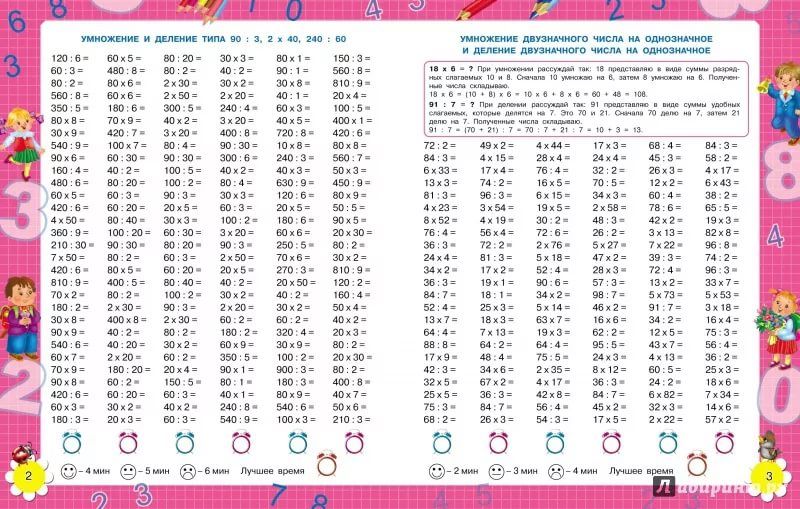
Я хотел убедиться, что ученики видят, из чего состоит каждая коробка. Например, первая ячейка (красная) 100 х 6, вторая ячейка (желто-оранжевая) 20 х 6, а третья ячейка 3 х 6. Затем я показал им, как это пишется и складывается. Я сделал это по двум причинам. Во-первых, потому что они увидят это снова, когда мы перейдем к частичным произведениям (далее), а во-вторых, потому что они увидят это позже, когда научатся использовать свойство дистрибутивности в алгебре (FOIL).
Частичные произведения как стратегия многозначного умножения
Большинство учителей, вероятно, знакомы с методом частичных произведений. В случае, если это не так, на самом деле нужно просто взять большее число и разбить его на расширенную форму, а затем умножить другой коэффициент на каждый из расширенных форм-факторов. Затем их суммируют, чтобы получить конечный продукт. (См. таблицу ниже.)
Вы заметите, что мои цвета вернулись. Когда это возможно, я использую цвета, чтобы различать каждый шаг.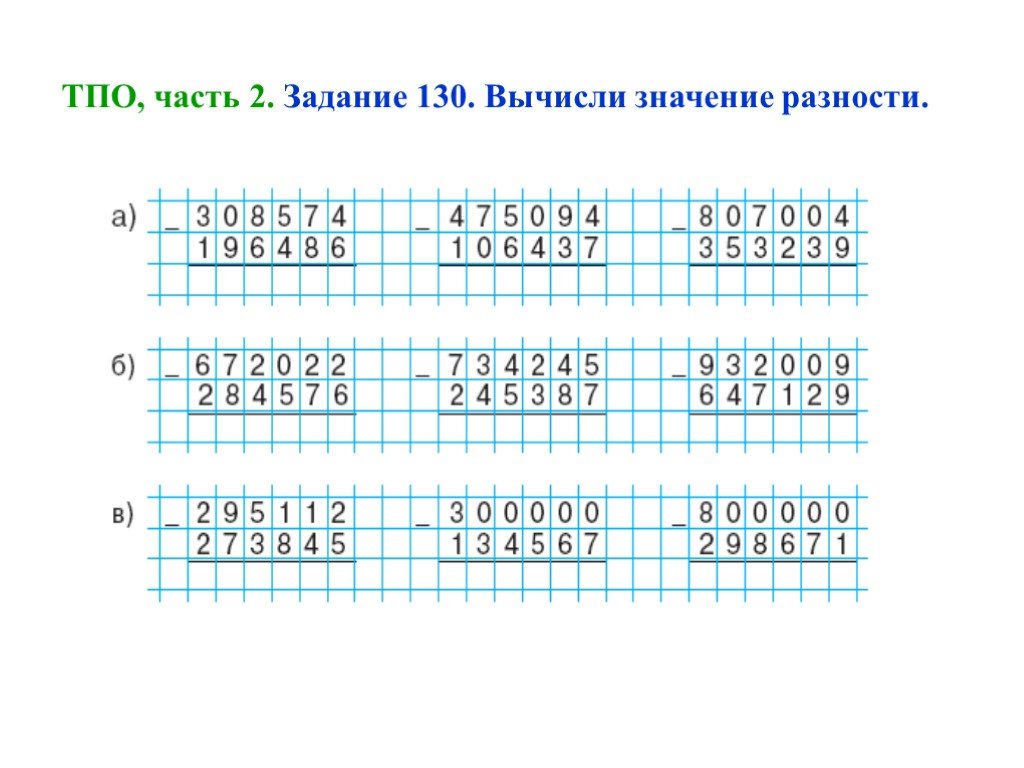
Напоминаю учащимся, что мы используем свойство дистрибутивности (что теперь не страшно!) и раскладываем наше большее число в развернутую форму. Затем мы умножаем каждый новый фактор по одному. Я всегда пишу каждый новый продукт рядом с задачей на умножение, чтобы ученики могли видеть, откуда я это взял. Затем, после того как мы нашли все продукты для каждого из них, мы суммируем их, чтобы найти наш конечный продукт. Эта стратегия также помогает позже при введении «заполнителя» в традиционный алгоритм.
Когда мы доходим до двузначных чисел, это то же самое, но я хотел бы ввести метод, называемый «метод галстука-бабочки». Как и прежде, учащиеся раскладывали оба фактора в развернутом виде. Затем они размножаются методом галстука-бабочки. Если вы посмотрите на иллюстрацию ниже, вы можете увидеть этот метод через использование цветов. На самом деле я заставляю своих учеников рисовать это на своих бумажных работах, чтобы помочь им не упустить ни одного множителя при умножении. Работая по методу галстука-бабочки, они записывают продукты для каждого из них.
После завершения они добавляют продукты вместе, чтобы получить конечный продукт.
Понятно, что если вы предпочитаете, чтобы ваши ученики начали подготовку к традиционному алгоритму, вы можете предложить им выполнить метод «галстук-бабочка» в движениях традиционного алгоритма, как показано в таблице ниже. В целом, смысл метода «галстук-бабочка» заключается в том, чтобы убедиться, что ни один фактор не упущен и не использован дважды.
Чтобы учащиеся действительно были готовы к умножению больших чисел с помощью традиционного алгоритма, они должны сначала пройти стратегии, требуемые Common Core. Это требует, чтобы мы также преподавали так, чтобы ученики учатся лучше всего. Если вы хотите, чтобы ваши учащиеся хорошо справлялись с многозначным умножением, вам нужно будет сформулировать концепции, сначала начав с конкретного метода использования площадной модели, работая с полуконкретной репрезентативной моделью блочного метода, а затем как в распределительном свойстве, так и в методе частичных произведений.
Использование только одного метода не поможет. Учащимся необходимо постепенное освобождение, прежде чем они будут готовы, иначе они просто не полностью поймут концепцию и не добьются успеха.
Получите БЕСПЛАТНО!
Чтобы помочь вашим учащимся практиковать эти стратегии, у меня есть для вас подарок! Нажмите здесь, чтобы скачать бесплатно!
Тогда ознакомьтесь с моими подробными планами уроков, играми и занятиями, которые сопровождаются этими якорными таблицами, чтобы вы могли сэкономить время на планировании уроков уже сегодня. Приобретите математическую мастерскую по умножению больших чисел для 4-го класса здесь, на моем веб-сайте, или найдите ее на TpT, нажав здесь.
Ознакомьтесь с этими разделами по математике для 4-го класса!
3,8 К акции
Развитие понимания многозначного умножения
Донна работала учителем, тренером по математике, интервенционистом и координатором учебной программы.
Часто выступая на государственных и национальных конференциях, она делится своей любовью к математике с мировой аудиторией через свой веб-сайт Math Coach’s Corner. Донна также является соавтором Guided Math Workshop.
По мере того, как мы начинаем вводить многозначное умножение, возникает тенденция сразу же погружаться в стандартный алгоритм. Хотя стандартный алгоритм является эффективной стратегией, он очень процедурный, и многие дети повторяют шаги, не понимая процесса. Отличный подход к построению концептуального понимания состоит в том, чтобы пройти через конкретные, репрезентативные и абстрактные этапы обучения. Давайте посмотрим, как это выглядит.
Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. С вас не взимается дополнительная плата, и я ссылаюсь только на книги и продукты, которые лично использую и рекомендую.
Конкретное (практическое) обучение
Первый конкретный шаг – создание равных групп с манипуляторами.
Поскольку мы используем большие числа, а многозначное умножение зависит от разрядности, имеет смысл использовать блоки с основанием десять. Чтобы решить 6 x 24, учащиеся просто составляют 6 групп по 24. Чтобы найти произведение, скорее всего, они начнут со счета десятков. Они могут сосчитать их десятками (10, 20, 30…120) или признать, что в каждой группе по 20 и считать по двадцать (20, 40, 60…120). Поощряйте несколько стратегий! Далее они будут считать единицы. Опять же, некоторые учащиеся могут считать все единицы один за другим, другие могут считать по 2, а третьи могут составлять группы по десять из единиц. Убедитесь, что учащиеся поделились своими стратегиями, и попросите их подумать о том, какие стратегии были более эффективными.
После того, как учащиеся попрактикуются в использовании метода равных групп, сообщите им, что у вас есть более эффективный способ организации материалов, позволяющий более эффективно считать десятки и единицы. Представьте модель области, используя блоки с основанием десять.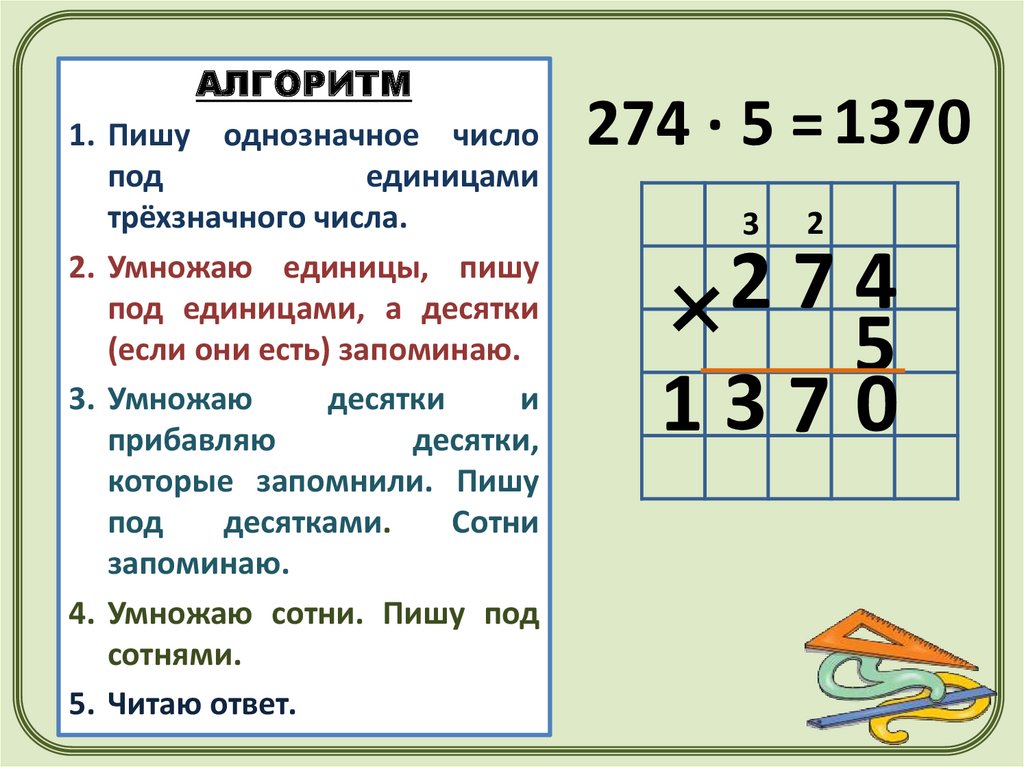
Обратите внимание, что 24 вверху и 6 внизу показывают нашу длину и ширину, и мы подсчитываем блоки внутри области. Делаем соединение, что у нас по-прежнему 6 групп по 24, но теперь группы равные ряды. На втором рисунке обратите внимание, что мы показали 24 в расширенной форме, 20 + 4, и мы сгруппировали десятки и единицы в группы по десять, чтобы сделать счет более эффективным.
Переход от конкретной модели к репрезентативной (графической)
Наш следующий шаг — перевести учащихся с модели конкретной области на иллюстрированную карандашно-бумажную версию. Я бы, наверное, добавил немного решения проблем в процесс. После того, как студенты построили модель площади, используя блоки с основанием 10 для 6 x 24, я показывал им разделенный прямоугольник без чисел. Проведите групповое обсуждение, спросив, что учащиеся замечают и интересуются новой моделью карандаша и бумаги. Спросите учащихся, как, по их мнению, эти два разделенных раздела связаны с нашей моделью конкретной области.
Когда они свяжут, что это похоже на десятки и единицы в модели площади, спросите Хммм, а как, по-твоему, тогда нам следует обозначить верхнюю и левую сторону? Оттуда вы можете попросить их предложить, как заполнить числа в двух разделах площадной модели.
Когда я буду готов использовать эту модель для умножения двух цифр на две цифры, я снова буду использовать решение задач. Представляя им задачу 24 x 16, я бы сказал, Хммм, интересно, как будет выглядеть наша модель области для этой задачи? Это немного другое. Тогда я позволил бы им работать в партнерстве, чтобы попытаться понять это. На самом деле это не так уж и много! Если оба фактора двузначные, мне нужна еще одна строка.
Использование модели области требует, чтобы учащиеся работали с числами, кратными 10 и 100. Вы можете проверить этот пост в блоге , чтобы узнать об упражнении, которое развивает беглость с числами, кратными 10 и 100. Еще одно замечательное занятие — заставить детей пропускать: считать кратно, так что вместо 3, 6, 9 и т.
д. они считают 30, 60, 90 и т. д. Это отлично работает со всей этой группой Искорка игра .
Переход от графического к абстрактному
Модель области представляет собой графическое представление, тесно связанное с алгоритмом, называемым частичными произведениями. Учащиеся, освоившие площадную модель, сделают этот переход плавным. Здесь вы видите две стратегии рядом, и легко увидеть сходство. Помогите учащимся организовать свое мышление, смоделировав, как показать умножение для каждого из частичных произведений, написав 6 x 4 рядом с произведением 24 и 6 x 20 рядом с произведением 120. Позвольте учащимся попрактиковаться в демонстрации модели площади и алгоритма частичных произведений. бок о бок, чтобы решать проблемы, пока вы не почувствуете, что они больше не нуждаются в иллюстрированной поддержке.
Наконец-то стандартный алгоритм!
Стратегии, ведущие к стандартному алгоритму, не предназначены для замены стандартного алгоритма. Они предназначены для понимания стандартного алгоритма.
Как только учащиеся будут уверенно использовать частичные произведения, мы можем поместить его рядом со стандартным алгоритмом и показать учащимся, что стандартный алгоритм — это просто короткий путь. Хотя в этом примере показано умножение 2 цифр на 1 цифру, он работает так же хорошо для 2 цифр на 2 цифры или 3 цифр на 1 цифру.
Вот она, дорога к стандартному алгоритму многозначного умножения с пониманием ! Помните, что этот процесс требует времени и практики с каждой новой моделью/стратегией. Иногда это вводит в заблуждение, потому что я описал все модели и стратегии в одном коротком посте. Но прежде чем переходить к следующей, вы должны убедиться, что учащиеся освоились с каждой моделью или стратегией. Это потребует дифференциации, поскольку мы знаем, что учащиеся не успевают с одинаковой скоростью.
Практика делает совершенным!
Конечно, вашим ученикам потребуется содержательная практика, и для этого у меня есть простая игра. Существуют версии для 2-значного на 1-значное, 3-значного на 1-значное и 2-значного на 2-значное.