Приемы письменного умножения трехзначных чисел на однозначные | Математика | 5 класс
Главная > Приемы письменного умножения трехзначных чисел на однозначные | Математика | 5 класс
Приемы письменного умножения трехзначных чисел на однозначные
Проиграть видео
На этом уроке вы вспомните распределительное и переместительное свойства умножения. Повторите, как умножают трехзначные числа на однозначные числа устно. Научитесь выполнять письменно умножение таких чисел. Сможете решить много интересных, развивающих заданий. Решите большое количество примеров для закрепления полученных навыков. Все желающие смогут научиться на практике применять приемы письменного умножения.
Распределительное свойство умножения
При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
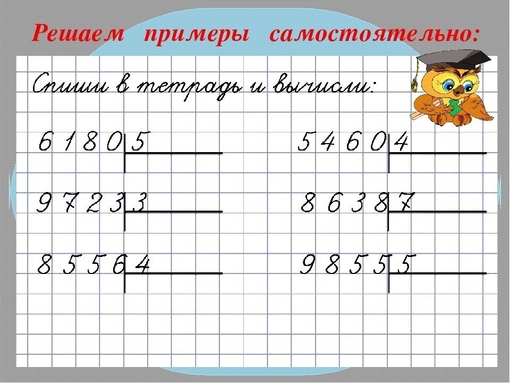
Задание № 1
Вычислите значения выражений.
1. 2.
Решение:
1. Заменим первый множитель суммой разрядных слагаемых. Умножим каждое слагаемое, а полученные результаты сложим.
2. Воспользуемся распределительным свойством умножения.
3. Решим первый пример столбиком. Для этого запишем второй множитель под единицами. Черта означает знак «равно».
4. Решим второй пример в столбик. При таком умножении начинать надо с единиц.
Вывод: при умножении трехзначного числа на однозначное число столбиком второй множитель надо записывать под единицами первого множителя. Черта заменяет знак «равно». Начинать умножение надо с единиц, потом умножать десятки и в конце – сотни.
Задание № 2
Вычислите значения произведений.
1. 2. 3.
Решение:
1. Воспользуемся переместительным свойством умножения – от перестановки множителей произведение не меняется, поэтому поменяем множители местами. Умножение выполним столбиком.
Умножение выполним столбиком.
2. Решим второй пример. Запишем четыре под единицами первого множителя. Вспомним о том, что при письменном умножении необходимо начинать с единиц, потом умножать десятки, и в конце – сотни. Также необходимо учесть, что черта под числами означает знак «равно».
3. При решении третьего примера поступим аналогичным образом и тоже поменяем местами множители.
Итог
Если умножать трехзначные числа на однозначные числа устно трудно, то можно умножить их столбиком.
- Помните о том, что, выполняя умножение столбиком, нужно начинать умножение с единиц. Затем умножают единицы разряда десятков. После – единицы разряда сотен.
- Если нужно умножить однозначное число на трехзначное число, то можно воспользоваться переместительным свойством умножения: поменять множители местами и выполнить умножение столбиком.
Список литературы
- Математика.
 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России).
4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России). - Истомина Н. Б. Математика. 4 класс. – М.: Ассоциация ХХІ век.
- Петерсон Л. Г. Математика, 4 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «kids.to-var.com» (Источник)
- Интернет-портал «igraemsami.ru» (Источник)
- Интернет-портал «math-prosto.ru» (Источник)
Домашнее задание
- ст. 6 № 11, ст. 10 № 34. Математика. 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011.
- Повторите распределительное и переместительное свойства умножения.
- Умножьте числа устно и письменно.
а) б) - * Вычислите произведение.

а) б) в) г) .
Оцените урок:
5/5
Онлайн-школа с индивидуальным уклоном С 1 по 11 класс
Подробнее
Умножение в столбик. Умножение и деление столбиком
В третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
Что является основой умножения
Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное.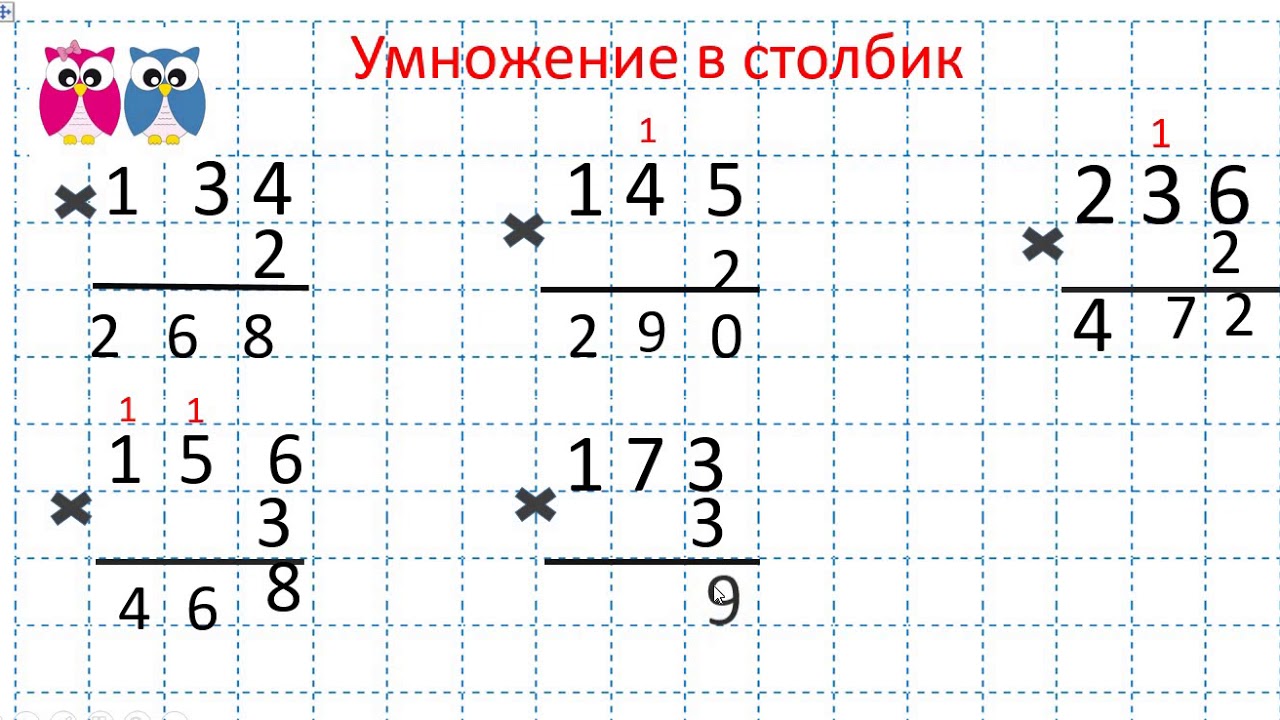 Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.
Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.
Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.
В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)
Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
Исследовательская работа детей
Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Этапы изучения умножения на многозначное число.
В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:
- самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
- для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
- отработка навыка умножения на круглые числа;
- использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
- операции с многозначными числами и умножение в столбик.

Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Задачи изучения умножения в курсе начальной школы
Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.
Какие же задачи ранее были решены учениками и их преподавателем?
- Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.

- Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
- Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2. Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Использование свойств умножения
Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.
Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.
Распределительное свойство умножения в этом случае выступает как универсальное.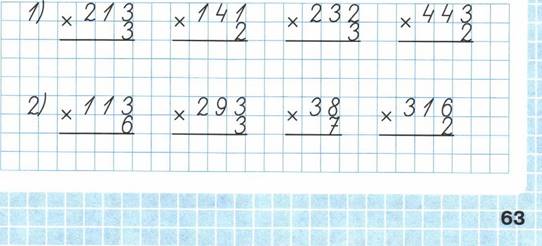 Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Алгоритм записи действия умножения в столбик
Запись умножения столбиком является самой компактной из всех существующих. Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».
Упражнения для формирования навыка
Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.
Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.
Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»
Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.
Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».
Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.
с примерами из жизни
Что такое массив умножения ? Разве это не более быстрый метод сложения? Таким образом, когда вы умножаете число на другое число, вы добавляете число столько же раз, сколько звонит другой номер. Умножение можно сделать проще, чем когда-либо, если вы выучите массив умножения. Они являются полезным представлением концепций умножения. Равномерно расставленные стулья в зрительном зале или марширующем строю изображают массивы.
Вы можете легко вычислить участвующих членов, если вы визуализируете их в строках и столбцах. Итак, что такое массив в умножении? Как массивы могут помочь быстрее решать задачи на умножение? Узнайте все о массиве умножения в статье ниже.
Вот что мы рассмотрим:
- Что такое массив при умножении?
- Как написать уравнения массива умножения?
- Как выполнить умножение массива с пропуском счета?
- Каковы преимущества массива умножения модели?
- Реальные примеры массива умножения
Визуальное видение вещей может помочь развить конкретное понимание важных математических концепций. Массив использует визуализацию элементов умножения в строках и столбцах. Массив — это расположение чисел, объектов или изображений в виде строк и столбцов. Строка располагается горизонтально (слева направо), а столбец (вверху и внизу) — вертикально.
Массив использует визуализацию элементов умножения в строках и столбцах. Массив — это расположение чисел, объектов или изображений в виде строк и столбцов. Строка располагается горизонтально (слева направо), а столбец (вверху и внизу) — вертикально.
Каждый столбец должен содержать одинаковое количество объектов в массиве, и то же самое относится к каждой строке. В них должно быть такое же количество объектов, как и в других рядах.
Как написать уравнения массива умножения?
Чтобы написать уравнение умножения массива, вы сначала считаете количество строк, а затем количество столбцов. Давайте рассмотрим несколько примеров ниже, чтобы понять массив умножения.
На следующем рисунке массив состоит из 2 строк и 4 столбцов смайликов. Его также можно описать как массив 2 на 4. Слово «по» можно представить крестом умножения.
Следовательно, математически вы записываете массив в виде 2 × 4. Дважды четыре равняется восьми, поэтому уравнение будет таким: 2 × 4 = 8
Этот массив состоит из 3 строк и 4 столбцов. Это массив 3 на 4, и вы можете записать его как 3 × 4. Уравнение умножения будет: 3 × 4 = 12
Это массив 3 на 4, и вы можете записать его как 3 × 4. Уравнение умножения будет: 3 × 4 = 12
Итак, из приведенных выше примеров вы можете видеть, что первое число представляет количество строк, а второе число представляет количество столбцов. Итак, второй массив — это 3 × 4, а не 4 × 3, хотя вычисленное произведение, т. е. 12, в любом случае будет одинаковым.
Как выполнить массив умножения с пропуском счета?
Что такое подсчет пропусков? Счет с пропуском — это метод прямого счета по числам, отличным от 1. Таким образом, если вам нужно считать с пропуском по номеру, вы будете продолжать прибавлять одно и то же число на каждом шагу к ранее полученному числу. Это похоже на многократное добавление. Предположим, вам нужно пропустить счет на 2, поэтому ваши ответы будут 4, 6, 8, 10, 12, 14 и так далее. Итак, каждый раз, когда вы прибавляете 2 к предыдущему числу, то есть прибавляете 2 к 4, чтобы получить 6, прибавляете 2 к 6, чтобы получить 8, и так далее.
Давайте возьмем следующий пример массива пончиков, чтобы понять, как пропустить счет для умножение массива на .
Приведенный выше массив состоит из трех строк, и в каждой строке пять пончиков. Итак, есть пять столбцов пончиков. Чтобы рассчитать общее количество пончиков, вы можете просто посчитать их. Но использование подсчета пропусков ускоряет процесс и делает его намного проще.
Здесь вы можете пропустить счет на 5 для каждой строки, чтобы подсчитать количество пончиков. В первом ряду пять пончиков, поэтому, если вы пропустите счет на 5, конец второго ряда составит десять, а конец третьего ряда даст пятнадцать, что и является вашим ответом. Это то же самое, что 3 × 5 = 15
На приведенном выше изображении вы также можете пропустить счет по столбцам. Вам придется пропустить счет на три, так как в каждом столбце есть три пончика. Таким образом, для пяти столбцов пропуск трехкратного счета будет выглядеть как 3, 6, 9, 12 и 15.
Интересно, что один массив может иметь два уравнения: одно для столбцов, а другое для строк. В приведенном выше примере уравнения умножения таковы:
Для строк: 3 × 5 = 15
Для столбцов: 5 × 3 = 15
Каковы преимущества массива умножения модели?
Умножение массивов имеет несколько преимуществ в понимании и решении математических задач. Не только математика, компьютерные языки, такие как Python, используют умножение массива NumPy для умножения массива. Вот некоторые из ключевых преимуществ умножения модели массива в математике:
Не только математика, компьютерные языки, такие как Python, используют умножение массива NumPy для умножения массива. Вот некоторые из ключевых преимуществ умножения модели массива в математике:
1. Умножение массива упрощает визуализацию задач
Это может быть отличным способом ввести умножение с практическими объектами, но это может быть утомительно, когда работа с большими числами или решение нескольких задач. Вы можете использовать массив бумажных точек, чтобы надеть L-образную крышку на верхнюю часть массива. Таким образом, вы можете показать любой факт умножения, который вы хотите. На следующем изображении показан массив точек и L-образная крышка.
Вы можете использовать массив точек и L-образную крышку следующим образом. Предположим, вы хотите объяснить, как выглядит 6 × 8, то есть 6 групп по 8. Наденьте L-образную крышку на массив точек, как показано ниже.
Теперь есть шесть рядов, и в каждом ряду восемь точек. Вы можете легко подсчитать общее количество точек в массиве как 6 × 8 = 48.
2. Умножение массива позволяет использовать стратегии вместо механического запоминания
Давайте рассмотрим пример 6 × 7, чтобы понять это. Ученикам становится трудно запоминать ответы на подобные умножения, но им становится легче, когда они используют 5 × 7 в качестве трамплина. Учащиеся в основном знакомы с числами, кратными пяти, с раннего возраста. Таким образом, становится намного проще, когда они видят 6 × 7 как еще одну группу из 7, чем 5 × 7. Им просто нужно сложить 35 + 7, чтобы найти ответ: 6 × 7 = 42.
3. Умножение массивов позволяет учащимся увидеть свойство коммутативности в действии
В соответствии со свойством коммутативности вы получите одинаковый ответ при умножении одних и тех же чисел в любом порядке. Например, если вы умножаете 4 × 7 или 7 × 4, оба дают один и тот же ответ: 28.
Используя умножение массива точек , вы можете объяснить факты умножения. Чтобы объяснить свойство коммутативности, поверните массив на 90 градусов. Массив точек покажет факт умножения, а общее количество точек не изменится.
Массив точек покажет факт умножения, а общее количество точек не изменится.
В предложении умножения есть несколько чисел, каждое из которых имеет особое имя. Числа, которые вы умножаете, называются множителями. Ответ, полученный путем умножения множителей, называется произведением.
6 × 7 = 42
Здесь 6 — это множитель, который представляет количество строк, множитель 7 представляет объекты в каждой строке, а произведение 42 представляет общее количество объектов.
Когда массив переворачивается на бок, все меняется следующим образом.
7 × 6 = 42
Здесь множитель 7 представляет количество строк, множитель 6 представляет объекты в каждой строке, а произведение 42 представляет собой общее количество объектов.
Порядок множителей меняется, но произведение остается прежним, демонстрируя математическое свойство, известное как коммутативное свойство умножения.
4. Использование массивов для больших чисел
Используя массивы, учащиеся могут легко изучить вычисления с большими числами, такими как 12 x 5. Массив можно разделить на полезные фрагменты. Например, 12 x 5 можно разбить для выполнения вычислений.
Массив можно разделить на полезные фрагменты. Например, 12 x 5 можно разбить для выполнения вычислений.
12 х 5 = (10 х 5) + (2 х 5).
Хотя рисование точек — хорошая техника для начинающих, она может быть утомительной. Метод пустого массива помогает решить сложные умножения, приняв неформальный способ. Они учат студентов, как использовать другие стратегии, такие как компенсация, для процесса умножения.
В следующем примере показан метод пустого массива для умножения. Здесь для вычисления 34 х 9 студент решил сделать 34 х 10. Далее он снимает 34 х 1, упрощая процесс.
Итак, 34 x 10 = 340
340 – 34 = 306
Вы также можете разбить 34 на 30 и 4. Затем вы вычтете 30 из 340, а затем 4 из 310.
5. Умножение Рабочие листы с массивами позволяют учащимся практиковать уравнения
Рабочие листы с массивами умножения — отличный способ попрактиковаться в уравнениях. Обычно учащимся предлагается заполнить уравнение для описания массива, как показано на рисунке ниже.
Реальные примеры массива умножения
Вы можете практиковаться в умножении массивов всякий раз, когда и где бы вы ни сталкивались с массивами. Они присутствуют повсюду вокруг вас.
Ниже приведены некоторые распространенные примеры массивов для умножения из реальной жизни:
- Лоток с яйцами
- Форма для выпечки маффинов
- Забор
- Коробка шоколада
- Блистерные упаковки лекарств
- Бутылки для воды в картонных коробках
- шахматная доска
- Матрицы также являются массивами
- Контакты на сотовом телефоне
- Меню ресторана
- Бланк вопросов представляет собой набор пронумерованных вопросов, где каждому вопросу присваивается определенное количество баллов.
Часто задаваемые вопросы
1. Как перемножить все значения в массиве?
Самый простой способ перемножить все значения в массиве — сначала преобразовать массив в список.
Затем вы можете использовать функцию карты, чтобы умножить каждое значение в списке.
Приведенный ниже код будет умножать каждое значение в массиве:
а = [1,2,3]
л = список(а)
л * 2
[2, 4, 6]
2. Что означает массив в математике?
Массив — это способ организации чисел, чтобы их можно было легко сортировать и искать. Это как электронная таблица Excel, но гораздо более продвинутая.
3. Какое предложение числа умножения представляет массив?
Массив представляет предложение на умножение 5 × 3 = 15
4. Как вы решаете задачи на умножение?
Чтобы решить задачу на умножение, вам нужно умножить числа в первом наборе скобок на числа во втором наборе скобок. Например, если вы хотите узнать, сколько будет 8 x 7, вы должны записать 8 и умножить на 7. В результате вы получите 56.
5. Что такое массив по математике 4 класс?
Массив – это набор чисел, организованных определенным образом. В 4-м классе по математике для решения задач используются массивы. В массиве все числа перечислены по порядку. Первое число называется номером индекса и говорит вам, сколько чисел в массиве. Вы используете порядковый номер, когда хотите сообщить своему учителю, какой номер идет где в задаче. 9
В 4-м классе по математике для решения задач используются массивы. В массиве все числа перечислены по порядку. Первое число называется номером индекса и говорит вам, сколько чисел в массиве. Вы используете порядковый номер, когда хотите сообщить своему учителю, какой номер идет где в задаче. 9
Я показываю быстрый способ решения задач на умножение двузначных чисел, когда один из множителей кратен десяти, например 78 × 50. В таких случаях ответ такой же, как 78 × 5 с нулем в конце. Мы можем сначала написать этот ноль, а затем умножить, как если бы мы умножали 5 × 78. (Конечно, тот же самый быстрый способ работает, если один из множителей кратен 100 или 1000 и т. д.)
Урок также включает одно слово проблема, связанная с площадью и расчетом, где нам нужно учитывать порядок операций.
См. также
Стандартный алгоритм: двузначное умножение
Математический мамонт Учебная программа 4 класса
Вернуться к списку видео 4 класса
Вернуться к оглавлению всех видео
ПОДОЖДИТЕ!
Получайте мою ежемесячную коллекцию математических советов и ресурсов прямо на свой почтовый ящик — и БЕСПЛАТНО получите книгу Math Mammoth! Электронная почта: Мы уважаем конфиденциальность вашей электронной почты.
Вы можете отказаться от подписки в любое время.
Математический мамонтовый турЗапутались в различных вариантах? Совершите виртуальный электронный тур по Math Mammoth! Вы получите: Первоначальное электронное письмо для загрузки вашего ПОДАРКА из более чем 400 бесплатных рабочих листов и образцов страниц из моих книг. Шесть других электронных писем «TOURSTOP» , которые объясняют важные вещи и часто задаваемые вопросы, касающиеся учебного плана Math Mammoth. (Узнай отличия между всеми этими разноцветными сериями!)Таким образом, у вас будет время переварить информацию в течение одной-двух недель, а также возможность лично спросить меня об учебной программе. Ежемесячный сборник советов по обучению математике и обновлений Math Mammoth (отказаться от подписки в любое время) Мы уважаем конфиденциальность вашей электронной почты. Примечание : СНАЧАЛА вы получите электронное письмо с просьбой подтвердить свой адрес электронной почты. | «Мини» курс обучения математикеЭто небольшой «виртуальный» двухнедельный курс, где вы будете получать электронные письма по важным темам преподавания математики, в том числе: — Как помочь учащемуся, отстающему от — Стоит ли использовать временные тесты — И многое другое! Вы также получите: ПОДАРОК из более чем 400 бесплатных рабочих листов и образцов страниц из моих книг в самом начале. Ежемесячный сборник советов по обучению математике и обновлений Math Mammoth (отказаться от подписки в любое время)Мы уважаем конфиденциальность вашей электронной почты. Примечание : СНАЧАЛА вы получите электронное письмо с просьбой подтвердить свой адрес электронной почты.  |
 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России).
4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России).
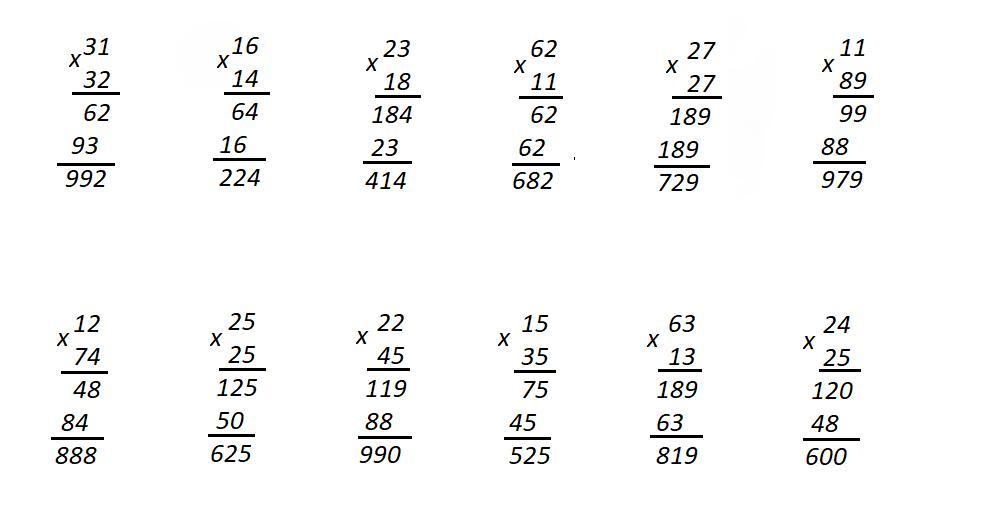
 Если вы не можете найти это электронное письмо с подтверждением, проверьте папку СПАМ/НЕПЛАХ.
Если вы не можете найти это электронное письмо с подтверждением, проверьте папку СПАМ/НЕПЛАХ.