Презентация к уроку математики «Деление столбиком», 3 класс
Урок математики
в 3 классе
Здравствуй, дорогой друг!
Эта презентация поможет тебе разобраться с новой темой. А какой ты узнаешь проходя каждое задание!
Желаю удачи!
Реши примеры в тетради:
7 * (14 + 27) =
(36 – 12) * 22 =
(120 : 20) * 52 =
2 : (104 – 52) =
— Какой пример оказался для тебя трудным?
— Почему именно в этом примере у тебя возникло затруднение при решении?
Тема урока:
«Деление в столбик»
— Для начала давай вспомним компоненты деления!
Запомни!
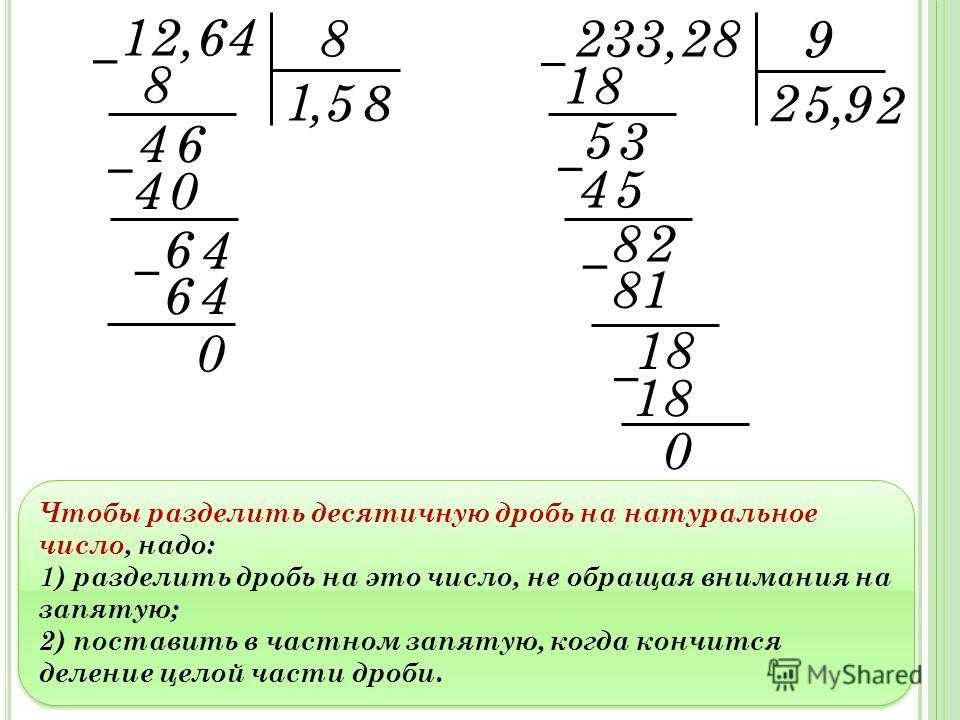
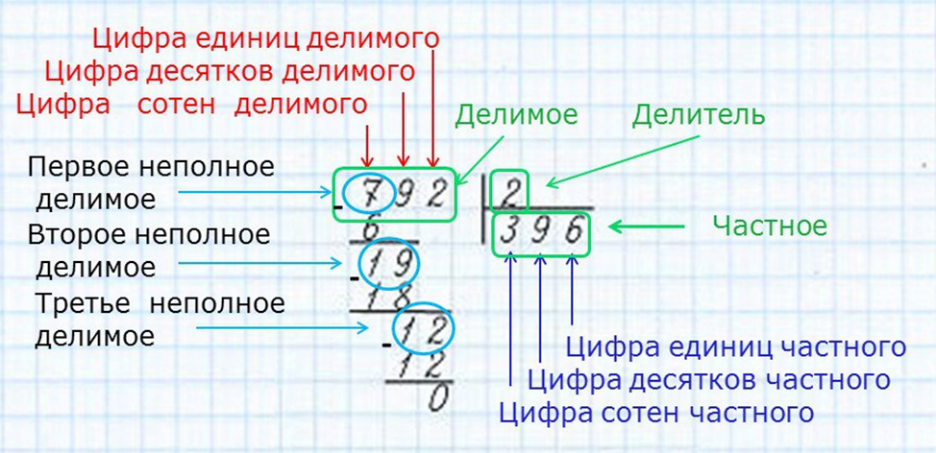
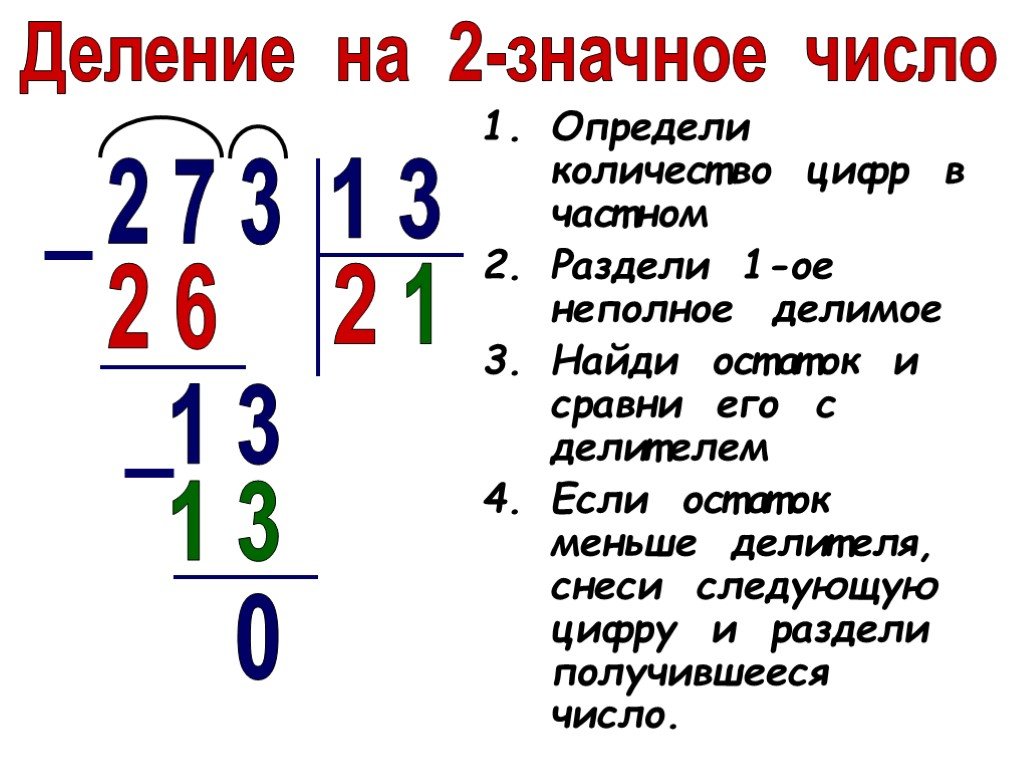
Алгоритм деления в столбик.
1. Записываем пример столбиком.
2. Ищем первое неполное делимое.
3. Считаем, сколько цифр будет в частном.
4. Делим неполное делимое.
5. Проверяем умножением.
6. Ищем остаток (он должен быть меньше делителя)
7. Сносим следующую цифру. Делим, проверяем умножением, ищем остаток и так, пока не разделим делимое.
8. Читаем ответ.
Потренируемся!
Реши задачи в тетради.
Задача 1. В 9 почтовых ящиков разложили 18 газет поровну. Сколько газет положили в каждый почтовый ящик?
Решение: 18 : 9 = 2 (г)
Ответ: По 2 газеты положили в почтовые ящики.
Задача 2. 24 апельсина раздали детям по 3 штуки каждому. Сколько детей получили апельсины?
Решение: 24 : 3 = 8 (д)
Ответ: 8 детей получили апельсины.
Возникли ли у тебя трудности при решении задач?
В этих задач мы использовали табличные случаи деления!
А теперь давай решим в тетради еще одну задачу.
Задача 3. В одной книге 65 страниц, а во второй в 5 раз меньше. Сколько страниц во второй книге?
— Сможем ли мы так же быстро решить эту задачу, как и прежние? Почему?
- Верно! Так как в таблицы умножения нет такого примера.
- Значит, нам нужно будет делить эти числа столбиком!
1. Сначала мы запишем пример: 65 : 5 =
2. Ниже мы будем записывать его решение в столбик:
- 5
5 1 3
15
15
0
3. Записываем ответ в пример выше.
4. Записываем ответ к задаче: 13 Страниц во второй книге.
Теперь попробуй решить задачи самостоятельно в тетради:
Задача 4. На овощебазу привезли 69 мешков моркови, а мешков с картошкой в 3 раза меньше. Сколько мешков картошки привезли на овощебазу?
Решение:
69 : 3 =
- 3
6
9
9
0
23
2 3
Ответ: 23 мешка картошки привезли на овощебазу.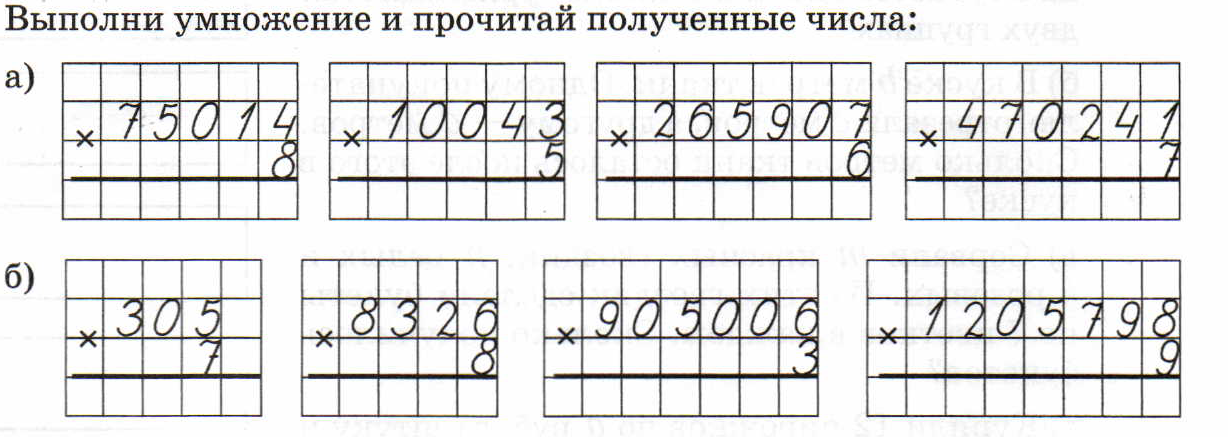
Домашняя работа.
Реши задачи в тетради используя деление в столбик.
Задача 1. Одна машина проехала 84 км, а вторая в 4 раза меньше. Сколько километром проехала вторая машина?
Задача 2. За неделю Петя прочитал 93 страницы, а Вася в 3 раза меньше. Сколько страниц прочитал Вася?
Спасибо за урок!
Математика 3 класс – какие темы нужно и важно выучить ребенку?
Третий класс – ответственное время для каждого ученика. Ведь скоро он перейдет в среднюю школу, и на его плечи ляжет значительно большая нагрузка. Если первоклассник практически повторял то, что проходил в подготовительном классе, то во втором классе малыш уже подготавливался к более серьезной программе по письму, математике, чтению.
Математика 3 класса предполагает значительное усложнение предыдущего материала, в частности, дети учатся применять таблицу умножения, внетабличные деление и умножение, изучают дроби и доли, решают более сложные примеры и задачи. Нагрузка на третьеклассника довольно большая, учитывая обширный материал и, как следствие, насыщенные уроки и сложные домашние задания.
Нагрузка на третьеклассника довольно большая, учитывая обширный материал и, как следствие, насыщенные уроки и сложные домашние задания.
Что проходят по математике в третьем классе
В третьем классе проходят довольно разнообразные темы. Хотя в основу их часто закладывают таблицу умножения, которую, чаще всего, малышу было задано выучить за лето. Кроме этого, ребята учатся решать примеры с использованием внетабличного деления и умножения, знакомятся с числами и действиями с ними. Для этого им нужно запомнить разряды и состав чисел.
В арсенале третьеклассника должно быть отработанное умение решать уравнения и выражения, арифметические, геометрические задачи повышенной сложности, где необходимо совершить более трех действий. Ему важно научиться хорошо решать не только простые задачи, но и составные.
Конечно же, учителя не обходят стороной и общематематическое развитие, уделяют внимание улучшению памяти, логического мышления, внимания и другим интеллектуальным способностям ребенка.
Умножение и деление
После того, как была закреплена таблица умножения, ученики переходят к изучению внетабличного деления и умножения. В частности, им объясняют, как выполнять эти действия в столбик, что такое деление с остатком.
Для этого происходит подробное изучение разрядов чисел, натуральных чисел, усвоение понятий «однозначное», «двузначное» и «трехзначное» число. А также ученик должен выучить, что такое множители и произведение, могут ли они меняться местами, и какими они могут быть.
Закрепив этот материал, третьеклассники переходят к умножению в столбик, где самое важное запомнить алгоритм. При делении также сначала важно выучить и закрепить на примерах понятия «делимое», «делитель», «частное», а также «неполное частное», которое появляется при делении с остатком.
Кроме того, детей постепенно начинают знакомить с единицами измерения, объяснять, что такое площадь и как ее найти.
Задачи и задания по математике для эффективного обучения
Как в школе, так и дома стоит уделять внимание не только подробному изучению тем школьной программы.
Натренировать интеллектуальные способности малыша помогут определенные задания, применение интересных приемов обучения, прохождение обучающих программ, познавательные игры. К ним можно отнести:
- головоломки;
- ребусы;
- кроссворды;
- математические загадки;
- задачки на сообразительность;
- настольные игры;
- игры на бумаге.
Для ученика 3 класса можно составить интересные примеры, предложить ему игры. Например, его заинтересует игра, в которой нужно проходить лабиринт, собирая числа на своем пути. Затем с собранными числами необходимо провести ряд арифметических действий.
Тренажер по математике в 3 классе
Кроме указанных способов развить у ребенка математическое мышление, можно использовать тренажер по математике за третий класс. Академия развития интеллекта AMAKids предлагает ученикам воспользоваться авторской методикой обучения математике «Амаматика», где предложено более 20 игр разной сложности. Каждый ученик может начать решать простые задачи, постепенно повышая уровень.
Академия развития интеллекта AMAKids предлагает ученикам воспользоваться авторской методикой обучения математике «Амаматика», где предложено более 20 игр разной сложности. Каждый ученик может начать решать простые задачи, постепенно повышая уровень.
Программа также отлично подходит для обучения в летнее время, когда ребенок не загружен школьными заданиями, но ему нужно повторить пройденный в прошлом году материал. Играя, малыш может освоить программу третьего класса, а также приобрести дополнительные знания.
«Амаматика» – это методика, которая позволяет изучить арифметику, геометрию, финансовую грамотность, основы программирования. Игровой формат обучения поможет детям эффективно улучшать свои интеллектуальные способности и заниматься с интересом.
Умножение и деление: Введение в деление
Урок 4: Введение в деление
/en/multiplicationdivision/video-multiplication/content/
Что такое деление?
Подразделение делит что-то поровну. Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Вы делите билетов между друзьями. Каждый друг получает равное количество билетов.
Видите, у каждого из них по 2 билета? Когда вы делите 10 билетов между пятью друзьями, вы создаете 5 равных групп по 2 билета.
В реальной жизни часто случаются деления. Например, рассмотрим ситуацию ниже.
Представьте, что у нас есть 6 кексов…
Представьте, что у нас есть 6 кексов… и 2 пустых лотка.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы будем делить кексы между двумя лотками.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим одинаковое количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
Шесть кексов были разделены на 2 равные группы.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
На каждом подносе по 3 кекса. Если вы начнете с шести кексов и разделите их на две равные группы, то в каждой группе будет по три кекса.
Написание выражений деления
В слайд-шоу вы видели, что мы разделили шесть кексов на две равные группы. Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления следующим образом:
6 / 2
Вы также можете написать выражение следующим образом:
6 ÷ 2
Любое выражение можно прочитать как шесть разделить на два . Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставили после первого числа — было 6 кексов, и мы разделили их на 2 группы.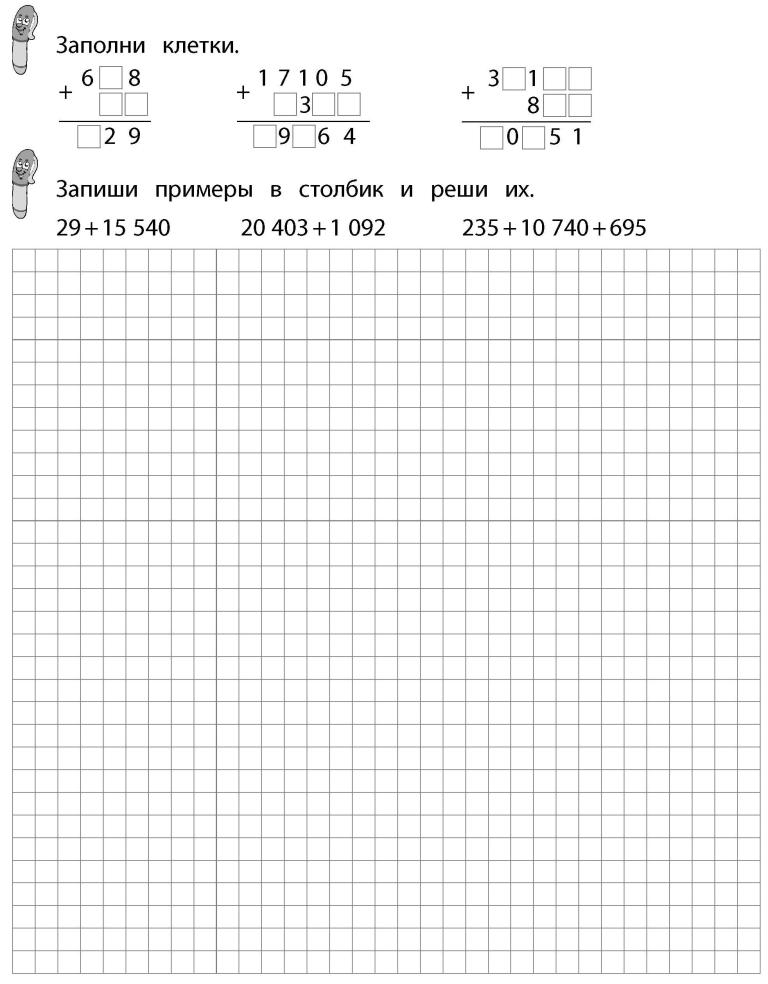
Многие жизненные ситуации можно выразить с помощью деления. Например, представьте, что вы расставляете 15 банок на 3 полках. Вы можете разделить, чтобы убедиться, что вы поставили одинаковое количество банок на каждой полке. Другими словами, 15 банок, разделенных тремя полками, или 15/3.
Попробуйте это!
Попробуйте настроить эти ситуации как выражения деления. Пока не пытайтесь их решить.
У учительницы есть 16 карандашей, которые она распределяет поровну между 4 учениками.
У флориста есть 18 роз, и он делит их поровну между 3 вазами.
У вас есть 6 угощений, которыми вы поровну делитесь с 3 собаками.
Решение задач на деление
Вы можете использовать , считая , для решения простых задач на деление. Например, допустим, у нас есть 12 саженцев. Решаем посадить их в два ровных ряда. Сколько растений в каждом ряду? Мы могли бы написать этот вопрос так:
12 / 2
Помните, что это выражение означает 12 разделить на два , или 12 саженцев разделить на 2 ряда.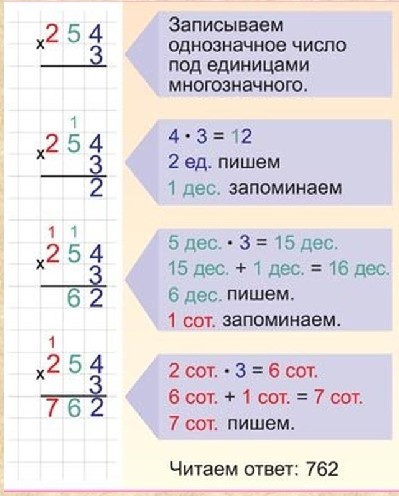 Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.
Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.
В то время как подсчет работает для задач, которые начинаются с маленьких чисел, задача, которая начинается с большого числа , может занять много времени, чтобы решить ее с помощью подсчета. По этой причине большинство людей запомнить простых задач на деление, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. С некоторой практикой вы сможете быстро запомнить ответы.
В разделе «Введение в умножение» вы познакомились с таблицей умножения на . На этом уроке вы использовали его для решения задач на умножение. Вы также можете использовать таблицу умножения для решения задач на деление.
Давайте начнем с проблемы, с которой мы уже знакомы. Как бы мы решили задачу о ростке с таблицей умножения?
Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.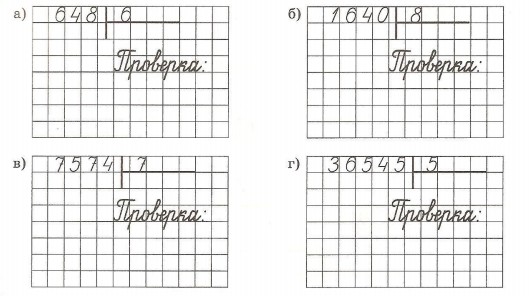
Помните, что каждое число в верхней части таблицы умножения находится в начале столбца .
Например, это столбец, который идет с 7.
Каждое число в левой части таблицы умножения является началом строки . Этот ряд идет с 9.
Давайте попробуем решить задачу о ростке: 12 / 2.
Сначала найдите число, на которое вы делите, справа от знака деления. В 12/2 мы делим на 2.
Найдите столбец 2.
Затем найдите число, которое вы делите, слева от знака деления. В 12/2 это 12.
Найдите 12 в колонке 2.
Найдите число в начале ряда, которое перекрывает 12. В данном случае это 6-й ряд.
Итак, ответ или частное для 12/2 равно 6.
Попробуем еще раз. На этот раз мы решим 15 / 5.
Сначала мы найдем 5-й столбец, так как мы делим на 5.

Затем мы найдем 15 в 5-м столбце, так как это число, которое мы делим.
Наконец, мы найдем число в начале строки, которое перекрывает 15. Это 3. Итак, 15/5 = 3.
Попробуйте!
Решите эти задачи на деление. Если вам нужна помощь, вы можете использовать таблицу умножения.
42 ÷ 7 =
5 ÷ 1 =
33 ÷ 3 =
Остатки
На предыдущих страницах мы делили числа поровну. Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что происходит, когда число нельзя разделить поровну?
Например, рассмотрим ситуацию ниже.
Допустим, у нас есть 10 билетов…
Допустим, у нас есть 10 билетов… которые мы делим между 3 друзьями.
Попробуем решить задачу 10 / 3.
Посмотрим, сколько билетов мы сможем дать каждому из наших друзей…
Посмотрим, сколько билетов мы сможем дать каждому из наши друзья.
 ..
..Посмотрим, сколько билетов мы можем подарить каждому из наших друзей… Один…
Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей… Один …
Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей… Один…
Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один… Два…
Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один. .. Два…
Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один… Два…
Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзья… Раз… Два… Три.
Что теперь? У нас 3 друга и остался только 1 билет.
Это означает, что 1 — это остаток или оставшаяся сумма.
Мы готовы написать наше частное.
У каждого друга по три билета, поэтому запишем 3.

Затем запишем остаток. Это 1. Видите, как мы написали это рядом со строчной буквой r ?
Итак, 10/3 = 3 r1. Мы можем прочитать это частное как три остатка один . 10 билетов, разделенных на 3 друзей, означает, что каждый друг получает 3 билета, а 1 билет остается.
Из слайд-шоу видно, что остаток (1) меньше, чем число, на которое мы делим (3). Так будет всегда, когда у проблемы есть остаток. Например, взгляните на каждую из этих задач ниже:
21/5 = 4 r1
Остаток от 1 меньше 5.
76/6 = 12 r4
Остаток от 4 меньше 6.
Если остаток больше, это означает, что остаток слишком велик. Вам нужно будет попробовать разделить еще раз. Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.
Практика!
Практика разделения с этими проблемами. Если хотите, можете воспользоваться таблицей умножить на .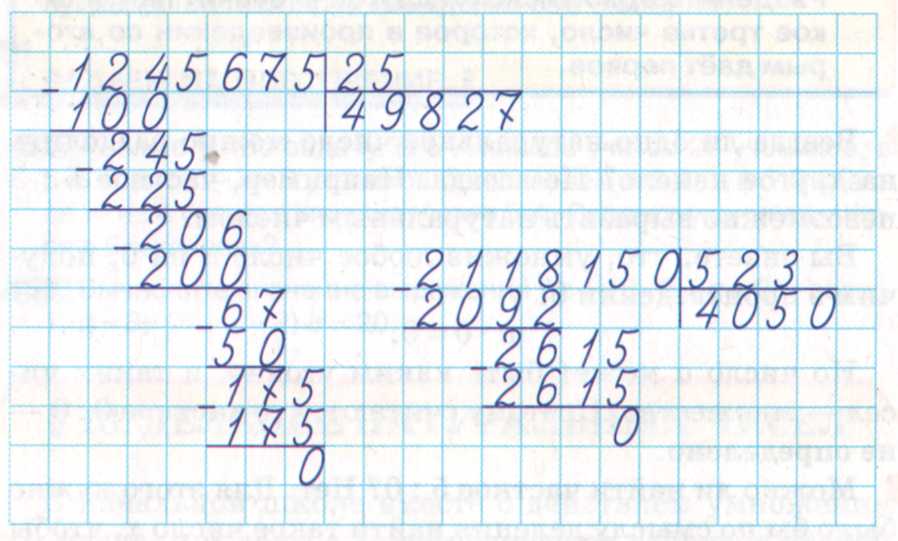 Есть 3 наборов задач по 5 задач в каждом.
Есть 3 наборов задач по 5 задач в каждом.
Установите 1
72 ÷ 9 =
64 ÷ 8 =
70 ÷ 10 =
55 ÷ 11 =
21 ÷ 3 =
Установка 2
35 ÷ 5 =
322. 322. 322. 322. 322. 322. =
72 ÷ 6 =
12 ÷ 2 =
28 ÷ 7 =
Набор 3
6 ÷ 1 =
81 ÷ 9 =
24 ÷ 3 =
49 ÷ 7 =
144 ÷ 12 =
ПродолжатьПредыдущий: Видео: Умножение
Далее:Длинная дивизия
/en/multiplicationdivision/long-division/content/
Математика / 3-й класс Common Core Math
Я ищу…
- Обзор
- Общий основной разговор
- Общая основная математика в детском саду
- Общая базовая математика 1-го класса
- Общая базовая математика 2-го класса
- Общая базовая математика 3-го класса
- Общая основная математика 4-го класса
- Общая базовая математика 5-го класса
- Важность числовых связей
- Числовая линия от Pre-K до 6 класса
- Вычислительная беглость
- Решение проблем в общем ядре
- K-5 Математика Часто задаваемые вопросы
- Общая базовая математика 6-го класса
- Общая базовая математика 7-го класса
- Общая базовая математика 8-го класса
- STEM-сайты для студентов
- Общая базовая математика средней школы
- Сайты для тестирования в старших классах
- Иллинойсская оценка информации и практики готовности
- Веселые математические задачи
- Математика дома К-5
- Математические развлечения и игры
- Учебные материалы средней школы
План третьего класса.
 учитель вашего ребенка в NWEA RIT.)
учитель вашего ребенка в NWEA RIT.)3-й класс Eureka Math/Engage New York Homework Help
Ваш 3-классник умножает и делит в пределах 100?
Математические навыки
Ваш 3-классник понимает, что означает деление?
Математические понятия
Может ли ваш 3-классник решать текстовые задачи на умножение и деление?
Реальные проблемы
0005
Third Grade Number and Operations База десяти
Чему научится ваш ребенок
Стандарт Что это значит?
Как это выглядит?Округление целых чисел до ближайших 10 или 100 (3.  NBT.1)
NBT.1)Набор уроков Сложение и вычитание в пределах 1000 (3.NBT.2) Набор уроков Умножение однозначных чисел на кратные 10. (3.NBT.3) Набор уроков - Разрядное значение: Расположение цифры в числе
- Значение : Значение цифры на основе ее разряда
- Продукт: результат умножения
- Фактор: число, которое умножается на другое число для получения произведения
- Кратность: произведение двух целых чисел
- Дополнение: Чтобы присоединиться к двум или более группам.
 2 + 3 = 5
2 + 3 = 5
- Addend: Число, добавляемое к другому в задаче на сложение.
В 2 + 3 = 5 2 и 3 являются слагаемыми.
- Сумма: Ответ на задачу на сложение. В 2 + 3 = 5, 5 это сумма.
- Вычитание: Чтобы найти разницу при сравнении двух групп или узнать, сколько предметов осталось, если убрать из группы предметы.
- Разница: Ответ на задачу на вычитание. В 8 – 3 = 5, 5 – это разница.
- Бросьте 2 числовых кубика. Найдите произведения сомножителей.
- Найдите числа в каталогах или газетах, а затем потренируйтесь округлять их до ближайших десятков и сотен.
- Бросьте числовой куб и потренируйтесь умножать это число на десять. После мастерства попробуйте с двумя числовыми кубиками.

- Потренируйтесь складывать и вычитать трехзначные числа.
- Покажите ребенку разное количество десятицентовых монет и попросите его попрактиковаться в подсчете суммы денег (4 десятицентовых монеты x 10 центов = 40 центов).
Изготовление чисел Расширенная форма (Нажмите на инструменты учителя) Игра Такума Грега Танга для сложения Целевой номер Интерактивная номерная линия Целевая сумма Сложение и вычитание Кратность 10 Игра Грега Танга «Разрыв на части» для сложения/вычитания/умножения/деления Операции третьего класса и алгебраическое мышление
Стандарт ХХХХХХХХХХХХ Как это выглядит?
Что это значит?
ХХХХХХХХХХХХХХХХХХХХПонять значение умножения (3.  OA.1)
OA.1)Набор уроков Понимание значения деления (3.OA.2) Набор уроков Решение текстовых задач с использованием умножения и деления (3.OA.3) Набор уроков Определение неизвестного целого числа в задаче на умножение или деление
(? X 8 = 24) (3.OA.4)Набор уроков Понимание свойств умножения (3.OA.5) Набор уроков Понимание деления как проблемы неизвестного фактора (3.OA.6) Набор уроков Свободно умножать и делить в пределах 100 (3.OA.7) Набор уроков Решение текстовых задач на сложение, вычитание, умножение и/или деление (3.  OA.8)
OA.8)Набор уроков Определение и объяснение арифметических шаблонов (3.OA.9) Набор уроков Разделение: на равные группы Делимое: число, которое делится на другое число Массив: расположение объектов в столбцах и строках Уравнение: математическое выражение, содержащее знак равенства, показывающее равенство двух выражений неизвестно Продукт: результат умножения Группировка: деление вещей на равные группы (комплекты) Частное: число без остатка, которое получается в результате деления Перегородка: для разделения на части Умножение: операция над двумя числами для нахождения их произведения.  Это можно рассматривать как повторное добавление.
Это можно рассматривать как повторное добавление.Несколько: произведение двух целых чисел Остаток: сумма, оставшаяся, когда целое число нельзя разделить на равные целые числа Фактор: число, которое умножается на другое число, чтобы получить произведение Вычитание: Чтобы найти разницу при сравнении двух групп или узнать, сколько предметов осталось, если убрать из группы предметы. Дополнение : Чтобы присоединиться к двум или более группам. 2 + 3 = 5 Addend: Число, добавляемое к другому в задаче на сложение.
В 2 + 3 = 5 2 и 3 являются слагаемыми.Сумма: Ответ на задачу на сложение. В 2 + 3 = 5, 5 это сумма. Разница: Ответ на задачу на вычитание. В 8 – 3 = 5, 5 – это разница. Оценка: число, близкое к точной сумме Вычисление в уме: вычисление чего-либо в уме - Изготовление массивов из предметов домашнего обихода (например, монет, бобов, кубиков)
- Выберите факты умножения или деления, чтобы проиллюстрировать или написать задачу.

- Охота на несколько наборов предметов в доме. Используйте многократное сложение и умножение, чтобы найти итоги.
- Отсортируйте монеты по типу, подсчитайте количество монет, а затем умножьте их, чтобы найти общую стоимость пенни (x 1), пятаков (x 5), десятицентовиков (x 10) и четвертаков (x 25).
- Бросьте 2 числовых кубика. Найдите произведения сомножителей.
- Подсчитайте количество предметов по 2, 3, 5 и 10.
- Бросьте 2 числовых кубика, чтобы определить коэффициенты. Создайте массив, чтобы найти продукт.
- Используйте калькулятор для решения текстовых задач на умножение и деление. Например, Кэлли хочет купить 20 яблок по 0,19 доллара каждое. Какова общая стоимость ее покупки? У Михаила 332 четверти. Он хочет разделить их на группы по 4 человека. Сколько групп он составит?
- Разыграйте задачи деления с помощью счетчиков. Например, у Брэда 12 кроликов. В каждую из 4 клеток он посадил одинаковое количество кроликов.
 Сколько кроликов посадил Брэд в каждую клетку?
Сколько кроликов посадил Брэд в каждую клетку? - Бросьте 2 числовых кубика и запишите семьи фактов. Например, для бросков 4 и 6 запишите: 4 X 6 = 24, 6 X 4 = 24, 24 ¸ 6 = 4, 24 ¸ 4 = 6.
- Попросите вашего ученика найти недостающий множитель. Например, 5 X какое число? = 75?
Подразделение Быстрая математика Уравнения баланса Словесные задачи на умножение и деление Значение умножения Семейные факты Алгебраическое рассуждение Неизвестный фактор Игра Какума Грега Танга на умножение Игра Грега Танга «Разрыв на части» для умножения Вокруг света Умножение пекарни Солнечный зайчик Рыбный магазин Хоумран Дерби Умножение метеоров Концентрация Математика Спейси Гран-при Кубок мира по футболу Раздел Факты Отдел сноса Унесенные бананы Тренировка Уэйда Отдел мытья посуды Муравьи идут маршем Группа авиакомпаний Автодром для водных видов спорта Отдел фруктовых побегов Маг-математик Измерения и данные третьего класса
ХХХХХХХХХХХХХХХХХ Как это выглядит?
Что это значит?
ХХХХХХХХХХХХХХХХХХХХГоворить и записывать время с точностью до минуты и понимать прошедшее время (3.  MD.1)
MD.1)Набор уроков 1
Набор уроков 2Измерение и оценка объемов жидкости (3.MD.2) Набор уроков 1
Набор уроков 2Создание графических изображений и гистограмм для представления данных (3.MD.3) Набор уроков 1
Набор уроков 2Измерьте линейкой с точностью до ¼ дюйма (3.MD.4) Набор уроков Область понимания. (3.МД.5) Набор уроков Измерьте площадь, считая квадраты. (3.МД.6) Используйте умножение, чтобы найти площадь прямоугольников. (3.МД.7) Набор уроков Решение задач, использующих периметр.  (3.МД.8)
(3.МД.8)Набор уроков - Аналоговые часы: Часы, которые показывают время, двигая стрелки по кругу в течение часов, минут и иногда секунд
- Площадь: Количество квадратных единиц, необходимых для покрытия плоской поверхности.
- Цифровые часы: Часы, которые показывают время с точностью до минуты с помощью цифр
- Расстояние: Расстояние между двумя заданными точками
- Истекшее время: Измерение количества времени от одного события до другого
- Оценка: Предположение или грубый расчет стоимости, количества или размера
- Масса: Мера количества материи в объекте.

- Мера: Использование стандартных единиц для определения размера или количества в отношении длины, высоты, площади, массы, объема, времени, периметра
- Периметр : Расстояние вокруг фигуры
- Масштабированная гистограмма: График, в котором для отображения данных используются столбцы
- Пиктограмма в масштабе: График, который использует изображения для отображения данных
- Стандартная единица: Традиционная единица измерения из метрической или общепринятой системы. Примеры включают дюймы, метры, фунты и т. д.
- Время: Секунды, минуты, часы, дни, месяцы, годы и т. д. Время отображается на часах или календаре.
- Объем: Количество места, занимаемое объектом
- Делитесь и обсуждайте таблицы и графики из газет и журналов.

- Проведите опрос среди членов семьи или друзей и постройте гистограмму или пиктограмму.
- Создайте физическую пиктограмму, используя реальные предметы (например, фрукты, овощи, крупы, кухонные принадлежности). Запишите график на бумаге. Измените масштаб, чтобы создать новую пиктограмму.
- Записывайте важные периоды дня (подъем, ужин, поход в школу, возвращение из школы и т. д.) и тренируйтесь определять, сколько времени прошло между занятиями.
- Рассчитайте прошедшее время, узнав, сколько времени требуется для выполнения повседневных действий (тренировка в футболе, выполнение домашних заданий, принятие душа и т. д.)
- Измерьте периметр и площадь комнат в вашем доме, чтобы определить, какие комнаты самые маленькие, а какие самые большие.
- Используйте бумагу с сеткой, чтобы сделать прямоугольники с одинаковыми периметрами. Определить площадь каждого прямоугольника.
- Заполните небольшую коробку кубиками (например, кубиками сахара), чтобы определить ее объем.
 Обдумайте несколько стратегий, чтобы определить объем.
Обдумайте несколько стратегий, чтобы определить объем.
Периметр и площадь С точностью до минуты Стандартный и метрический вес Размер в дюймах Периметр и площадь Эквивалентные измерения Множественные измерения Истекшее время Создать график Вероятность со спиннером Чтение графика Медиана и мода на линейном графике Найти медиану Меры для жидкостей Сосуд для сбора Можешь заполнить? Номер и эксплуатацию третьего класса
Фракции
Что ваш ребенок узнает
.
Как это выглядит?
Что это значит?Понять значение дроби. (3.NF.1) Поместите дробь в числовую прямую (3.NF.2) Набор уроков Понимание эквивалентных дробей (3.NF.3) Урок 1
Урок 2
Урок 3- Знаменатель: нижнее число в дроби. Он показывает, на сколько равных частей было разделено множество или целое
- Эквивалентные дроби: две или более дроби, обозначающие одну и ту же сумму
- Дробь: число, обозначающее часть целого или часть группы
- Самый большой: самый большой в группе
- Наименьший : самый маленький в группе
- Номер Строка: строка с равноотстоящими делениями, обозначенная цифрами
- Числитель: первое число в дроби.
 Он сообщает, сколько равных частей целого или группы учитываются
Он сообщает, сколько равных частей целого или группы учитываются
- Заказ: расположение по размеру, количеству или стоимости
- Отправляйтесь на охоту за фракциями! Ищите предметы быта, разделенные на равные части (доли целого и доли набора). Запишите дроби.
- Бросьте числовые кубики, чтобы составить дроби. Нарисуй получившиеся дроби. Расположите полученные дроби по порядку на числовой прямой.
- Определение дробей во время еды. Например, вы съели 1/2 яблока, 3/4 стебля сельдерея, 1 бутерброд с тунцом и 2/3 стакана молока.
- Потренируйтесь составлять эквивалентные дроби.
- Постройте дроби на числовой прямой.
фракционная модель иллюминаций.png Geicko_Fractions.  png
pngидентифицироватьфракции.png Эквивалентные дроби Основные фракции Соответствующие дроби — части набора Основные фракции Геометрия третьего класса
Стандарт Как это выглядит?
Что это значит?Понимать атрибуты четырехугольников. (3.G.1) Набор уроков Разделите фигуры на равные части.  (3.G.2)
(3.G.2)Набор уроков - Конгруэнтные: Фигуры одинакового размера и формы
- Параллелограмм: Четырехугольник с двумя парами параллельных сторон и двумя парами равных сторон
- Многоугольник: Замкнутая двухмерная фигура с прямыми линиями
- Четырехугольник: Многоугольник с четырьмя сторонами
- Прямоугольник: Двухмерная фигура с 4 сторонами и 4 прямыми углами, противоположные стороны параллельны
- Ромб: Двумерная фигура с 4 равными сторонами и 4 углами (не обязательно равными), противоположные стороны параллельны
- Квадрат: Двумерная фигура с 4 равными сторонами и 4 прямыми углами
- Дробь: Число, обозначающее часть целого
- Трапеция: Двухмерная фигура, имеющая 4 стороны и 4 угла, одна пара сторон параллельна
- Прямой угол: Угол, образующий прямой угол
- Используйте сетку для создания конгруэнтных фигур.

- Определите, опишите и классифицируйте различные предметы домашнего обихода в виде объемных фигур.
- Определите углы, которые меньше, равны и больше прямого угла.
- Используйте танграммы для изготовления фигурок самолетов.
- Нарежьте кусочки пряжи, чтобы сделать отрезки. Измерьте каждый сегмент в дюймах (с точностью до четверти дюйма) и сантиметрах.
- Наблюдайте за звездами и создавайте воображаемые отрезки, соединяя звезды (точки). Создание геометрических фигур.
- Отправляйся на поиски формы! Ищите геометрические фигуры в вашем доме и обществе. Создайте диаграмму, чтобы показать свои выводы.
Объем Четырехсторонние свойства Сортировщик форм Угадай твердую фигуру Формы изображений Соответствие форме Геометрия Бинго Степени ошибки <h3>Необходим Javascript</h3> <p>Для редактирования страниц необходимо включить Javascript в браузере.


 ..
..
 учитель вашего ребенка в NWEA RIT.)
учитель вашего ребенка в NWEA RIT.) NBT.1)
NBT.1)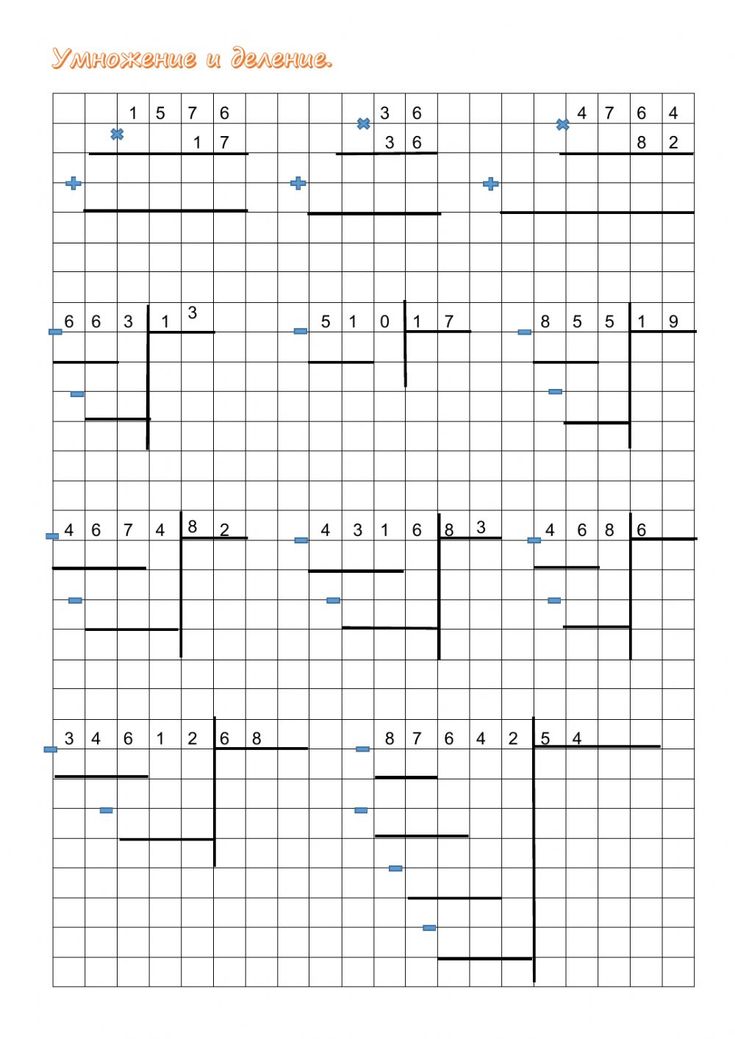 2 + 3 = 5
2 + 3 = 5
 OA.1)
OA.1) OA.8)
OA.8)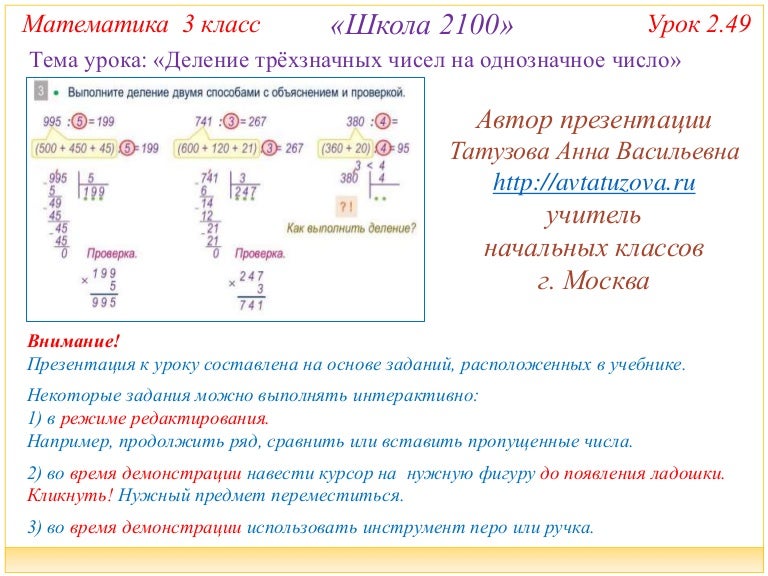 Это можно рассматривать как повторное добавление.
Это можно рассматривать как повторное добавление.
 Сколько кроликов посадил Брэд в каждую клетку?
Сколько кроликов посадил Брэд в каждую клетку? MD.1)
MD.1) (3.МД.8)
(3.МД.8)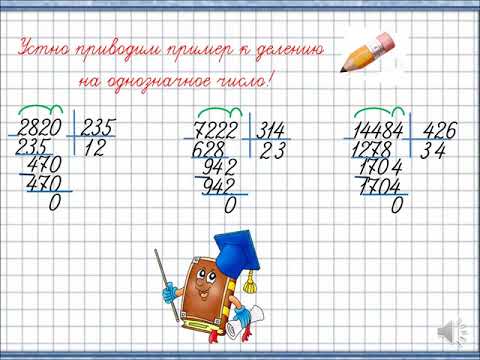

 Обдумайте несколько стратегий, чтобы определить объем.
Обдумайте несколько стратегий, чтобы определить объем.
 Он сообщает, сколько равных частей целого или группы учитываются
Он сообщает, сколько равных частей целого или группы учитываются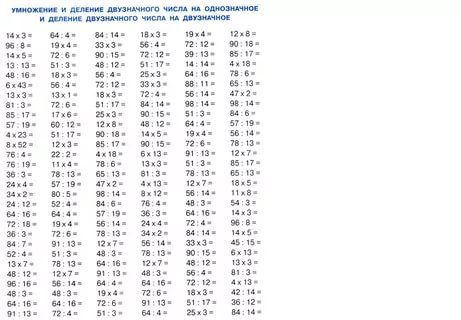 png
png (3.G.2)
(3.G.2)
