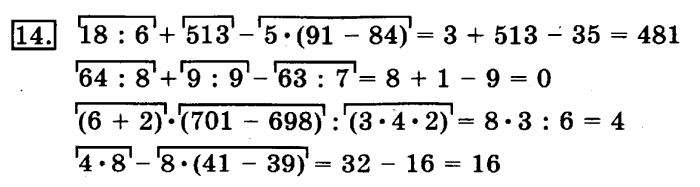Примеры по математике 4 класс на порядок действий со скобками сложные с умножением и делением: Примеры на порядок действий с ответами для 4 класса (часть 2). | Тренажёр по математике (4 класс) по теме:

Примеры на порядок действий с ответами для 4 класса (часть 2). | Тренажёр по математике (4 класс) по теме:

Примеры на порядок действий для 4 класса с ответами (продолжение)

43. (982-709)х852-9608=

     

44. (738+906)х375-287453=

     

45. (1867-298)х304-92888=

46. (228+757)х74+581618=

       

47. 221х384:(52014-51975)=

48. 1508х214: (48000-47884)=

49. 1269х406: (2109-1968)=

50. 7007х428: (81405-81191)=

     

51. 444х209: (10105-9957)=

     

52. 344х627: (9107-8978)=

     

53. 276х775: (30026-29796)=

     

54. 648х475: (1458-1306)=

55. 816х502: (8511784913)=

     

56. 288х703: (405060-404916)=

     

57. (912:114+6440:23):16=

58. (7294:14+12960:27):91=

     

59. (131364:41-19000:25):52=

     

60. 16728:204х (328-4267:17):11-419=

     

61. (7327:17+17х35+150):8=

     

62.  (814х107-452х145+32568):93=

     

63. (457+824) х7+1003=

64. (1125+875)х18+4328=

     

65. (331540:605+369000:450) :36х1008:171-129=

66. (953+627)х12+12040=

Ответы

43. (982-709)х852-9608=222988

      1) 273         2) 232596

44. (738+906)х375-287453=329047

      1) 1644        2) 616500

45. (1867-298)х304-92888=384088

      1) 1569        2) 476976

46. (228+757)х74+581618=654508

       1) 985         2) 72890

47. 221х384:(52014-51975)=2176

      1) 39           2) 84864

48. 1508х214: (48000-47884)=2782

      1) 116         2) 322712

49. 1269х406: (2109-1968)=3654

      1)141          2)515214

50. 7007х428: (81405-81191)=14014

      1) 214         2)2998996

51. 444х209: (10105-9957)=627

      1) 148        2) 92796

52. 344х627: (9107-8978)=1672

      1) 129        2) 215688

53. 276х775: (30026-29796)=930

      1) 230        2) 213900

54.  648х475: (1458-1306)= 2025

      1) 152        2) 307800

55. 816х502: (8511784913)=2008

      1) 204        2) 409632

56. 288х703: (405060-404916)=1408

      1) 144        2) 202464

57. (912:114+6440:23):16=18

1) 8        2) 280        3) 288

58. (7294:14+12960:27):91=11

      1) 521        2) 480        3) 1001

59. (131364:41-19000:25):52=47

      1) 3204      2) 760         3) 2444

60. 16728:204х (328-4267:17):11-419=155

      1) 251        2) 77       3) 82        4) 6314        5) 574

61. (7327:17+17х35+150):8=147

      1) 431       2) 595       3) 1026        1176

62. (814х107-452х145+32568):93=582

      1) 87098       2) 65540       3) 21558       4) 54126

63. (457+824) х7+1003=9970

      1) 1281         2) 8967

64. (1125+875)х18+4328=40328

      1) 2000        20 36000

65. (331540:605+369000:450) :36х1008:171-129=95

1) 548       2) 820       3) 1368       4) 38        5) 38304        6)224

66.  (953+627)х12+12040=31000

1)1580       2) 18960

Раскрытие скобок и порядок действий до 1000 (сложные примеры)

130,00 ₽

Примеры на порядок действий в пределах 1000: содержат 2 пары скобок и 5 математических действий: сложение, вычитание, умножение и деление. С ответами. Для печати А4.

Количество товара Раскрытие скобок и порядок действий до 1000 (сложные примеры)

Артикул: i-2363 Категория: Для учебы Метки: Порядок действий, 3 класс, 4 класс

• Описание
• Детали
• Отзывы (0)

Описание

Программа «Сложные примеры на порядок действий до 1000» представляет собой тренажер счета, где нужно выполнить вычисления в правильной последовательности действий.

Эти задания выделятся отдельным этапом, так как они способствуют развитию логического мышления ребенка. Именно поэтому нужна практика, чтобы закрепить понимание очередности вычислений.

Формируются примеры на порядок действий в пределах 1000, которые включают скобки (2 ед.), а также от пяти и более математических операций (сложение, вычитание, умножение, деление).

Программа написана в Excel с помощью макросов. Формируются карточки на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. В конце карточки формируются ответы на примеры, которые можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Генератор примеров по математике будет очень

удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл, сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Другие программы, которые помогут закрепить навыки счета в пределах 1000:

• • Порядок действий в пределах 1000 (все действия)
  • Цепочки примеров в пределах 1000 (все действия)
  • Умножение и деление по типам (табличное, внетабличное, круглых чисел)
  • Сложение и вычитание в столбик
  • Умножение и деление в столбик
  • Выражения с именованными числами

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Задание на неделю 4 класс

  140,00 ₽В корзину

• Сложение и вычитание в столбик

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Выражения с именованными числами (разные единицы измерения)

  90,00 ₽В корзину

• Умножение и деление в столбик

  Оценка 4.67 из 5

  100,00 ₽В корзину

• Задачи на движение (разные виды)

  100,00 ₽В корзину

• Продолжить ряд чисел

  125,00 ₽В корзину

• Умножение и деление по типам (табличное, внетабличное, круглых чисел)

  120,00 ₽В корзину

• Задание на неделю 3 класс

  130,00 ₽В корзину

• Деление с остатком на число (с выбором делимого и делителя)

  Оценка 4. 00 из 5

  80,00 ₽В корзину

Простая причина, по которой вирусное математическое уравнение поставило Интернет в тупик

Были ли разные способы обучения порядку операций причиной путаницы? 1 кредит

Вот уже около десяти лет математики и преподаватели математики обсуждают конкретную дискуссию, уходящую корнями в школьную математику, которая не собирается стихать.

Дебаты, освещаемые Slate, Popular Mechanics , The New York Times и многие другие издания сфокусированы на уравнении, которое стало настолько «вирусным», что, в конечном счете, его смешали с другими явлениями, которые «сломали» или «разделили» Интернет.

На случай, если вы еще не взвесились, сейчас самое время посмотреть, на каком вы месте. Пожалуйста, ответьте на следующие вопросы:

8÷2(2+2)=?

Если вы похожи на большинство, ваш ответ был 16 и вы ошеломлены, кто-то может найти другой ответ. Если, конечно, вы не похожи на большинство других, и ваш ответ был 1, и вы в равной степени сбиты с толку, видя это по-другому. Не бойтесь, в дальнейшем мы объясним окончательный ответ на этот вопрос и почему следует запретить способ написания уравнения.

Наш интерес был вызван тем, что мы провели исследование соглашений о следовании порядку операций — последовательности шагов, выполняемых при столкновении с математическим уравнением — и были немного сбиты с толку тем, о чем идет речь.

Очевидно, что ответ…

Два реальных ответа на одну математическую задачу? Ну, если есть что-то, что мы все помним из уроков математики: это не может быть правдой!

Многие темы возникли из множества статей, объясняющих, как и почему это «уравнение» сломало Интернет. Много обсуждался ввод выражения на калькуляторах, некоторые из которых запрограммированы на соблюдение определенного порядка операций.

Другие, немного уклоняясь, предполагают, что оба ответа верны (что смешно).

Самая доминирующая тема просто сосредоточена на реализации порядка операций в соответствии с различными аббревиатурами. Некоторые комментаторы заявили, что непонимание людей было связано с неправильной интерпретацией заученной аббревиатуры, которой учили в разных странах, чтобы запомнить порядок операций, таких как PEMDAS, иногда используемый в Соединенных Штатах: PEMDAS относится к применению круглых скобок, возведению в степень, умножению, делению, сложению и вычитанию.

У человека, который следует этому порядку, 8÷2(2+2) станет 8÷2(4) благодаря тому, что он начинает со скобок. Тогда 8÷2(4) становится 8÷8, потому что нет степеней, а «M» означает умножение, поэтому они умножают 2 на 4. Наконец, согласно «D» для деления, они получают 8÷8= 1.

Канадцев, напротив, можно научить запоминать BEDMAS, что означает применение скобок, возведения в степень, деления, умножения, сложения и вычитания. У кого-то, кто следует этому порядку, 8÷2(2+2) станет 8÷2(4) благодаря началу со скобок (так же, как скобки). Тогда 8÷2(4) становится 4(4), потому что (нет степеней), а «D» означает деление. Наконец, согласно «М» для умножения, 4(4)=16.

Если бы проблема была правильно представлена ​​как 8 ÷ 2 × (2 + 2) = ?, не было бы горячих споров. Предоставлено: Иган Дж. Чернофф, предоставлен автором.

Не пропускать знак умножения

Для нас выражение 8÷2(2+2) синтаксически неверно.

Мы утверждаем, что ключом к спору является то, что символ умножения перед скобками опущен.

Такое упущение является соглашением в алгебре. Например, в алгебре мы пишем 2x или 3a, что означает 2 × x или 3 × a. Когда буквы используются для переменных или констант, знак умножения опускается. Рассмотрим знаменитое уравнение e=mc ^2, , что предполагает вычисление энергии как e=m×c ^2.

Таким образом, настоящая причина того, что 8÷2(2+2) сломала Интернет, связана с практикой опускания символа умножения, которая была неуместно перенесена в арифметику из алгебры.

Несоответствующий приоритет

Другими словами, если бы выражение было правильно «расшифровано», то есть представлено как «8 ÷ 2 × (2 + 2) = ?», не было бы распространения вируса, двойственности, ни сломанного интернета, ни жарких споров. Не весело!

В конечном счете, пропуск символа умножения приводит к неправильному приоритету умножения. Все комментаторы согласились с тем, что добавление терминов в скобки или круглые скобки было подходящим первым шагом. Но возникла путаница из-за близости 2 к (4) по отношению к 8 в 8÷2(4).

Мы хотим, чтобы было известно, что писать 2(4) для обозначения умножения неуместно, но мы видим, что это делается всегда и везде.

Красивый символ умножения

Есть очень хороший символ для умножения, так что давайте использовать его: 2 × 4. Если вы не фанат, есть и другие символы, например 2•4. Используйте любой из них по своему усмотрению, но не пропускайте.

Таким образом, к сведению, дебаты по поводу одного против 16 окончены! Ответ 16. Дело закрыто. Кроме того, в первую очередь не должно было быть никаких дебатов.

Предоставлено Разговор

Эта статья переиздана из The Conversation под лицензией Creative Commons. Прочитайте оригинальную статью.

Цитата : Простая причина, по которой вирусное математическое уравнение поставило Интернет в тупик (2022, 29 августа) получено 24 апреля 2023 г. с https://phys.org/news/2022-08-simple-viral-math-equation-stumped.html

Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.

Базовый порядок операций (DMAS)

Введение

При упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.

Давайте разберемся с этим на примере.

Предположим, мы хотим найти значение 2 + 3 x 5

Есть два способа найти значение приведенного выше выражения.

В первом методе будем двигаться слева направо, решая выражение в указанном порядке. Это означает, что сначала мы найдем сумму 2 и 3. Мы получим, 2 + 3 = 5.

Теперь у нас есть 2 + 3 x 5 = 5 x 5

Теперь мы найдем произведение 5 на 5 чтобы получить ответ как 25. Следовательно, мы имеем

2 + 3 x 5 = 25 ……………………………….. ( 1 )

Теперь найдем значение этого выражения другим способом.

Сначала мы найдем значение 3 x 5 и добавим это произведение к 2. Таким образом, мы получим

3 x 5 = 15 и 15 + 2 = 17

Следовательно, теперь у нас есть

2 + 3 x 5 = 17 ………………………… ( 2 )

Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.

Каков основной порядок операций?

Порядок операций можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. Без последовательного порядка операций можно допустить большие ошибки во время вычислений. Существует ряд правил, определяющих порядок операций в зависимости от задействования операторов, скобок, показателей степени и других математических символов для операций. Это правило известно как DMAS, где

D означает деление (÷)

M означает умножение (x)

A означает сложение (+)

S означает вычитание (–)

Давайте разберемся с правилом более подробно.

Что такое DMAS?

MDAS, как определено выше, является основным порядком операций. Другими словами, он определяет порядок, в котором должны выполняться операции над числами, когда возникают ситуации, когда в выражении имеется на две операции больше, чем две. Итак, у нас порядок операций такой – 

Рассмотрим пример. Предположим, мы хотим найти значение 3 + 5 x 2.

Здесь у нас есть два оператора, а именно ( x ) и ( + ). Мы знаем, что в математике мы можем выполнять операции между двумя числами только за один раз. Если у нас есть более 2 чисел, результат первой операции используется для выполнения следующей операции. Итак, в приведенном выше примере необходимо выполнить две операции: (3 + 5) и (5 x 2). Нам нужно решить, с какой из них начать. Здесь вступает в действие правило MDAS.

Из этого правила видно, что умножение предшествует сложению. Поэтому сначала выполним операцию умножения. Полученный таким образом результат будет добавлен к 3. Шаги, связанные с этим процессом, будут — 

3 + 5 x 2

 = 3 + 10

 = 13

Следовательно, 3 + 5 x 2 = 13

Рассмотрим другой пример.

Пример

Упростите следующее выражение, используя порядок операций –

6 + 5 – 4 x 2

Решение

Нам дано выражение 6 + 5 – 4 x 2

Важно отметить, что здесь задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо.

Следовательно, мы имеем

6 + 5 – 4 x 2

 = 6 + 5 – 8 (Здесь мы решили 4 x 2, что дало нам результат 8)

= Затем мы сложим 6 и 3, чтобы получить 9. Итак, мы имеем

6 + 5 – 8 = 11 – 8  = 3

Следовательно, 6 + 5 – 4 x 2 = 3

Использование скобок в порядке операций

Мы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.

Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении. Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –

24 ÷ 3 x 4

= 8 x 4 = 32

Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как

24 ÷ ( 3 x 4 )

Теперь в соответствии с порядком действий сначала разгадаем скобки, чтобы получить,

 24 ÷ ( 3 x 4 )

= 24 ÷ 12

 = 2

В сложных выражениях иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, потому что чаще всего используются разные типы скобок)

Скобки Имя

( ) Круглые скобки

{ } Скобки или фигурные скобки

[ ] Скобки или квадратные скобки

Здесь важно отметить, что левая часть каждого символа скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.

Удаление скобок

Для упрощения выражений, содержащих более одной скобки, мы будем использовать шаги, описанные ниже –

1. Посмотреть, содержит ли данное выражение винкулум или нет. Если винкулум присутствует, выполните операции с красным цветом, в противном случае перейдите к следующему шагу. Винкулум — это горизонтальная линия, расположенная над выражением, чтобы показать, что все, что ниже линии, является одной группой, например, $\overline{2\: x\: 3}$.
2. Теперь найдите самую внутреннюю скобку и выполните в ней операции.
3. Удалите самую внутреннюю скобку, выполнив следующие действия: 
   1. Если скобке предшествует знак плюс, удалите ее, записав ее термины как есть.
   2. Если скобке предшествует знак минус, измените положительный знак внутри нее на отрицательный и наоборот.
   3. Если между числом и символом группировки нет знака, то это означает умножение.
   4. Если перед некоторыми скобками стоит число, то мы умножаем число внутри скобок на число вне скобок.
4. Найдите ближайшую внутреннюю скобку и выполните в ней операции. Удалите второй в направлении, используя правила, указанные в предыдущих шагах. Продолжайте этот процесс, пока не будут удалены все скобки.

Давайте разберем приведенные выше шаги на примере.

Пример

Упростим: 37 – [ 5 + { 28 – ( 19 – 7 ) } ]

Решение

Нам дано выражение, 37 – [ 1 9 – 28 – ( 1 ) } ]

Мы будем использовать порядок операций для решения данного выражения.

Сначала мы удалим самую внутреннюю скобку, чтобы получить

37 – [ 5 + { 28 – 12 } ] …………………… [ Удаление самой внутренней скобки ( ) ]

Далее мы удалим фигурные скобки, чтобы получить

37 — [ 5 + 16 ] …………………………. [ Удаление фигурных скобок ]

Теперь мы удалим квадратные скобки, чтобы получить,

37 – 21 …………………………… [удаление квадратных скобок ]

Наконец, мы найдем разницу между 37 и 21, чтобы получить 16.

Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] приведет к 16.

Как решать выражения, используя порядок операций?

Теперь, когда мы поняли, что мы подразумеваем под порядком операций, давайте узнаем о шагах, связанных с решением математических выражений с использованием порядка операций. Необходимые шаги: 

1. Всегда начинайте с вычисления всех выражений в круглых скобках

Прежде всего, мы должны искать удаление любых группирующих символов в алгебраическом выражении. Это означает, что в верхней части списка не забывайте всегда   упрощать все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.

2. Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни

После удаления скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении. Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.

3. Выполните умножение и деление, начиная слева направо

Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.

4. Наконец, аналогично выполните сложение и вычитание, начиная слева направо.

Давайте разберемся на примере.

Пример Найдите значение выражения 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )

Решение Нам дано выражение 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 ). Нам нужно решить ее с помощью MDAS.

Так как данное выражение содержит скобки; мы сначала решим скобки. Мы получим 

4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )

Теперь в скобках сначала решим раздел деления

4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 )

Далее в самой скобке решим умножение, чтобы получить

4 ( 10 + 3 × 4 – 2 × 2 )

Теперь внутри скобки решим сложение, чтобы получить

4 ( 10 + 12 – 4 ) 

Далее в скобках мы сложим числа 10 и 12, а затем вычтем из результата 4, чтобы получить

4 ( 22 – 4 )

После того, как скобка решена, возьмите число из снаружи и решить часть «Из» умножением:

= 4 × 18

= 72

Таким образом, 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )= 72

Используемые шаги можно представить в виде таблицы: 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 ) Отдел 4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 ) 90663 4 5 Умножение 4 ( 10 + 3 × 4 – 2 × 2 ) Сложение 4 (10 + 12–4) Вычитание 4 (22–07 4) 3 3 908 4 Ответ = 4 x 18 72

Применение порядка операций в реальной жизни

Мы узнали, что в математике порядок операций помогает найти правильное значение выражения. Однако это не ограничивается задачами по математике. Порядок операций имеет значение и в повседневной жизни. Например, вы используете фиксированный порядок действий для приготовления блюда. Точно так же в химических реакциях необходимо соблюдать определенный порядок, чтобы получить желаемые результаты. Возвращаясь к математике, есть много повседневных дел, в которых используется порядок операций MDAS.

Давайте разберемся на примере.

Пример

Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Сколько всего он платит?

Решение

Нам известно, что Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Нам нужно узнать, сколько Джон платит за рубашки и джинсы. Чтобы найти это, мы должны сначала разместить все значения в виде выражения. Мы получим,

Цена 2 рубашек + Цена пары джинсов – Скидка = Общая стоимость, уплаченная Джоном

Следовательно, 

Общая стоимость, уплаченная Джоном = 2 x 8 + 20- – 3

Здесь мы видим, что есть задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо. Следовательно, мы получаем,

Общая стоимость, уплаченная Джоном = 16 + 20 – 3 = 36 – 3 = 33 £

Следовательно, общая стоимость, уплаченная Джоном за 2 рубашки и пару джинсов, = 33 фунта стерлингов

Теперь мы научились решать выражения, включающие более одного математического оператора. Но что, если в выражении используются скобки. Поступим ли мы так же или внесем некоторые дополнения в правило? Давайте узнаем.

Ключевые факты и сводка

1. Порядок работы можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.
2. MDAS — это основной порядок операций, где MDAS, где M означает умножение (x), D означает деление (÷), A означает сложение (+), S означает вычитание (–).
3. Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении.
4. Правила порядка операций: – 
   • Всегда начинайте с вычисления всех выражений в скобках
   • Упростите все показатели степени, такие как квадратные корни, квадраты, куб и кубические корни.
   • Выполните умножение и деление, начиная слева направо.
   • Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
5. Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении.
6. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.