Этапы урока | Деятельность учителя | Характеристика деятельности учащихся УУД | |||||||||||||||||||||
1 этап. Мотивационно-организационный момент.
| Проверка готовности учащихся к уроку. На доске запись: «С малой удачи начинается успех» — Какое ключевое слово в этом высказывании? (УСПЕХ) — Что необходимо для успешной работы на уроке? (быть внимательным, заинтересованным…) -Я желаю Вам успешно поработать на уроке. Посмотрите друг на друга, улыбнитесь и пожелайте успеха. — В конце урока каждый из вас оценит свою работу. | Личностные УУД: | |||||||||||||||||||||
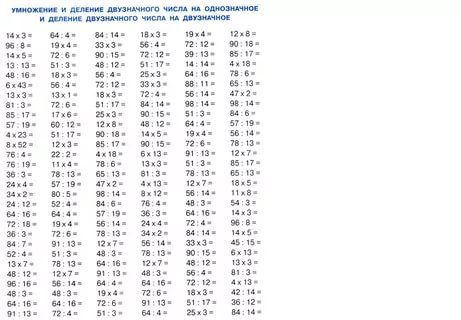
2 этап. Актуализация и фиксирование индивидуального затруднения в пробном действии. Цель: находить значение выражений, проговаривая каждый этап мыслительных действий. | Устный счет. Наш урок начнем с устного счета. Выбирайте выражение и объясняйте ход выполнения действия. 1000 ⋅ 275 = 68 ⋅ 100 = 35 ⋅ 7= 34 ⋅ 29 = 2 ⋅ 19 ⋅ 5 = 250 ⋅ 40 = 240 ⋅ 30= (Возникает проблема при решении последнего примера 34 ⋅ 29=) | Познавательные УУД Регулятивные УУД Коммуникативные УУД Личностные УУД | |||||||||||||||||||||
3 этап. Выявление места и причины затруднения. Постановка учебной задачи, темы урока.
| — В чем трудность, почему не решили последний пример? (Не решали такие примеры, не получается решить тем способом, который нам знаком.) -Чем отличается новый пример от тех, что мы решали раньше? (Здесь двузначные множители, а раньше были однозначные или двузначные с нулями на конце.) — Итак, какую цель поставим перед собой? (Познакомиться с новыми видами примеров. Научиться умножать на двузначное число.) -Сформулируйте тему урока? (Умножение на двузначное число) — Откройте учебник на с. 44 и сравните формулировку темы урока, сказанную вами и обозначенную в учебнике. | Познавательные УУД Регулятивные УУД Коммуникативные УУД | |||||||||||||||||||||
4 этап. Построение проекта выхода из затруднения. Цель: осуществлять выход из затруднительной ситуации на основе ранее полученных знаний. | — Возвращаемся к нашему примеру. Какие у вас есть предложения по решению проблемы? 34 ⋅ 29= (Нужно представить одно из чисел в виде суммы разрядных слагаемых, а потом умножать. Например: 34⋅ (20 + 9) = — Какое свойство умножения мы при этом будем использовать? (Умножение числа на сумму.) — Хорошо! Повторите последовательность операций при умножении числа на сумму) (Ученики проговаривают алгоритм действий: Множитель 29 представим в виде суммы разрядных слагаемых Умножим число 34 на 20. Умножим число 34 на 9. Полученные результаты сложим. 34 ⋅ 29 = 34 ⋅ (20 +9) = 34⋅ 20 + 34⋅ 9 = 680 + 306 = 986 (Пример записывается на доске) | Познавательные УУД Регулятивные УУД Коммуникативные УУД Личностные УУД | |||||||||||||||||||||
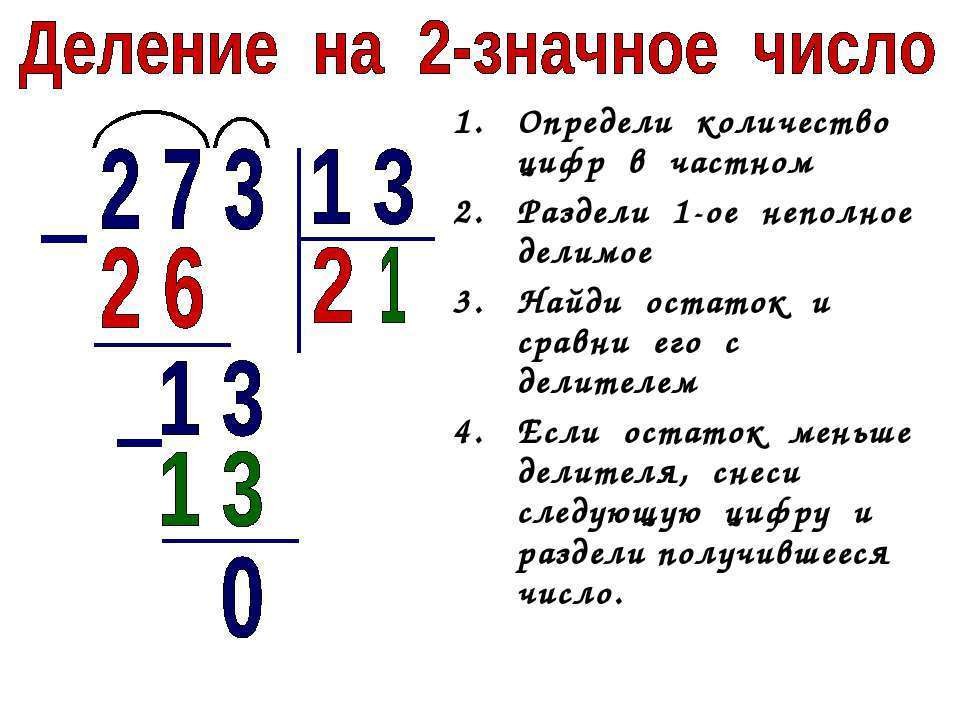
5 этап. Цель: выполнять столбиком умножение двузначного числа на двузначное, соблюдая алгоритм действий. | — С сегодняшнего дня мы будем пользоваться записью умножения на двузначное число в столбик. — Давайте подведем первые итоги: как же умножать в столбик на двузначное число, используя прием умножения числа на сумму. (Ученики должны сами вывести правило: Чтобы умножить двузначное число на двузначное, можно умножить это число сначала на единицы, а затем на десятки и полученные произведения сложить) × 3 4 2 9_ 3 0 6 Первое неполное произведение + 6 8__ Второе неполное произведение 9 8 6 — Зная алгоритм письменного умножения на однозначное число, составьте алгоритм умножения на двузначное число. 1. Второе неполное произведение 68 дес. (или 680) начнем подписывать под десятками, оставив свободное место для указания нуля единиц. При этом ноль приписывать не будем. (Ученикам раздаются алгоритмы умножения двузначного числа на двузначное)
| Предметные УУД Регулятивные УУД Коммуникативные УУД | |||||||||||||||||||||
Физминутка Цель: релаксация, снятие напряжения, смена вида деятельности. | Видеоролик. | ||||||||||||||||||||||
6 этап. Первичное закрепление с проговариванием во внешней речи. Цель: выполнять по образцу алгоритм письменного умножения на двузначное число; контролировать выполнение каждого действия (шага) алгоритма; | — А теперь выполните задание №157 на стр. 44. 1-ый и 2-ой примеры с комментированием у доски, остальные самостоятельно. 19⋅ 46 27 ⋅ 35 42 ⋅ 23 25 ⋅ 25 — Проверьте правильность выполнения примеров по образцу. (Взаимопроверка по эталону на доске). | Предметные УУД Регулятивные УУД Коммуникативные УУД | |||||||||||||||||||||
7 этап. Работа в парах. | Работа в парах (Предлагается выполнить задание № 1 первому ученику, а задание №2 второму ученику. Затем обменяться тетрадями и провести взаимопроверку с последующим объяснением всему классу) Задание №1. Рабочий ежедневно изготавливает 28 деталей. Сколько деталей изготовит этот рабочий за 24 дня? Задание № 2. В школе 32 класса, по 25 учащихся в каждом. Сколько всего учащихся в этой школе? | Предметные УУД Познавательные УУД Регулятивные УУД Коммуникативные УУД Личностные УУД | |||||||||||||||||||||
8 этап. Включение в урок задание на повторение. | Самостоятельная работа.
| Познавательные УУД Регулятивные УУД Коммуникативные УУД Личностные УУД | |||||||||||||||||||||
9 этап. Подведение итогов урока. Рефлексия. Цель: обобщить полученные на уроке сведения. | — Что нового узнали? — Какую цель ставили перед собой? (Познакомиться с новыми видами примеров. — Достигли мы цели? Как умножают на двузначное число? (Рассказывают алгоритм) Оцените свою деятельность. -Прочитайте данные высказывания. 1) Я всё понял(а), но у меня остались вопросы. 2) Я всё понял(а), могу работать по алгоритму. 3) Я всё понял(а), могу работать по алгоритму, могу объяснить другому. -Если вы согласны с первым утверждением, нарисуйте красный кружок, если согласны со вторым- желтый, а если с третьим — зеленый. | Регулятивные УУД Личностные УУД | |||||||||||||||||||||
10 этап. Домашнее задание. Цель: выполнять вариативные задания | Вариативность домашнего задания. Выучить алгоритм. Тем, кто выбрал 1 и 2 утверждение: составить 5 примеров, где требуется выполнить умножение на двузначное число. Тем, кто выбрал 3 утверждение: составить задачу, чтобы в её решении были действия с умножением на двузначное число. |
Умножение двузначного числа на двузначное
Урок математики.
Тема: «Умножение двузначного числа на двузначное»
4 класс
Тип урока: закрепление новых знаний.
Цель: знакомство с приемом письменного умножения на двузначное число.
Задачи:
сформировать понятие об умножении многозначного числа на двузначное;
усвоить алгоритм письменного умножения данного вида;
совершенствовать навыки решения текстовых задач;
продолжить отрабатывать навыки устных и письменных вычислений;
обеспечить устойчивую мотивационную среду, интерес к изучаемой теме;
воспитывать уважение к историческому наследию русского народа.
Планируемые результаты:
Познавательные: на уроке дети развивают навыки умножения на двузначное число используя запись в столбик; применяют эти знания, работая с примерами.
личностные: воспитывать умение работать в коллективе, продолжится формирование интереса к предмету, к учебной деятельности.
регулятивные: формулировать тему и цель урока, научится принимать и сохранять учебную задачу; самостоятельно формулировать задание; оценивать результат своих действий; получит возможность научиться: адекватно воспринимать оценку своей работы учителем, товарищами.
коммуникативные: оформлять свои мысли в устной и письменной форме; высказывать свою точку зрения; научится использовать в общении правила вежливости; получит возможность строить понятные для партнера высказывания; работать в паре.
Формы познавательной деятельности:
фронтальная
самостоятельная
в группах
Оборудование: карточки, листки самооценки, учебник и его задания.
ХОД УРОКА
1. Организационный момент:
Дети стоят полукругом.
— Собрались ребята в круг,
Слева друг и справа друг.
Вместе за руки возьмёмся
И друг другу улыбнёмся.
— Я передаю улыбку …, …, и т.д.
— А теперь передадим улыбку нашим гостям.
— Мы рады приветствовать Вас на нашем уроке математики.
— А теперь ребята, давайте с хорошим настроением возьмёмся за работу.
Соберитесь в группы те дети, у кого на листочках одинаковые числа.
1 группа – 1, 2 группа – 2, 3 группа – 3, 4 группа – 4.
Я желаю всем сегодня сделать много хороших дел. А урок наш проходит под девизом: «Математику учить – ум точить.»
Мы отправляемся в путешествие по стране Математике.
— Математика – это одна из самых важных и древних наук. Слово «математика» пришло из древнегреческого языка. Мантейн – это значит учиться, приобретать знания. Математика призвана развивать логическое мышление, внимание, память. Недаром её называют гимнастикой ума.
-Ребята, а что от вас требуется, чтобы урок прошел успешно?
внимание, трудолюбие, усидчивость, хорошие знания, сообразительность, память
— Желаю Вам успешно поработать на уроке. Пожмите друг другу руки и пожелайте успеха. Я уверена, что сегодня на уроке вы отлично потренируете логику, мышление, память, смекалку и другие качества.
Пожмите друг другу руки и пожелайте успеха. Я уверена, что сегодня на уроке вы отлично потренируете логику, мышление, память, смекалку и другие качества.
Смело иди вперёд, не стой на месте.
Что не сделаешь один, сделаем вместе.
На партах у каждого из вас лежит листок самооценки, вы помните, как с ним работать.
(если уверен в знаниях по данному вопросу ставит +;
сомневается ставит + -;
не уверен ставит -).
№ | Вид задания | Выполнение задания |
1 | Устный счёт. | |
2 | Решение задачи на движение. |
|
3 | Решение геометрических задач. | |
4 | Знание алгоритма умножения двузначного числа на двузначное. |
|
5 | Решение выражений с применением алгоритма. |
|
6 | Решение математических выражений самостоятельно. | |
7 | Решение логических задач. |
|
-Не забывайте определить для себя, как вы усвоили материал, выявить свои собственные затруднения, чтобы затем их устранить.
— Давайте вспомним о чём мы говорили на прошлом уроке. (о взаимосвязи скорости, расстояния и времени)
— Объясните, что обозначают выражения стр. 63 учебника №7
— Молодцы откройте тетради запишите число и классная работа.
— Продолжим урок тренировкой мышления и логики.
ЗАДАЧИ-ШУТКИ
1. Пассажир такси ехал в село. По дороге ему навстречу проехали 5 грузовиков и 3 автомашины. Сколько машин ехало в село?
Сколько машин ехало в село?
2. Автобус едет от города до аула 2 часа, а обратно 120 минут. Как объяснить такую разницу?
Какие задачи мы сейчас решили? (Логические)
Логика нужна нам в жизни?
Сравни устный счёт выбери удобный способ вычисления №4 стр. 63
На уроке математике надо уметь не только рассуждать, но и быть очень внимательным.
Заполни пропуски в таблице №9 стр. 63 распечатать
Перед нами ДОЛИНА НОВЫХ ЗНАНИЙ.
2. Актуализация знаний
Устный счёт с доски выберите удобный для вас способ решения:
1000 • 275 = 35 • 7= 46 • 73=
2 • 19 • 5 = 240 • 30=
(Возникает проблема при решении последнего примера 46 • 73 =)
— В чем трудность, почему не решили последний пример?
— Этот пример надо решать письменно.
— Какая же сегодня у нас тема урока? Сформулируйте её.
«Умножение двузначного числа на двузначное»
— Какие цели мы поставим перед собой?
— Давайте повторим алгоритм умножения двузначного числа на однозначное.
Памятка.
Умножу первый множитель на число единиц.
Подписываю под единицами.
Получу первое неполное произведение.
Умножу первый множитель на число десятков.
Подписываю под десятками.
Получу второе неполное произведение.
Сложу неполные произведения
Читаю ответ.
А перед нами ГОРА ИСПРАВЛЕНИЯ ОШИБОК.
Решение учебной задачи
Работа в парах (на листочках)
Аня и Ваня решали примеры столбиком. Посмотрите, что у них получилось:
1 | 6 | 3 | 1 | 6 | 3 | |||||||||
х | 4 | 5 | х | 4 | 5 | |||||||||
8 | 1 | 5 | 8 | 1 | 5 | |||||||||
+ | 6 | 5 | 2 | + | 6 | 5 | 2 | |||||||
7 | 3 | 3 | 5 | 1 | 4 | 6 | 7 | |||||||
— Почему получили разные результаты?
-Какой результат должны получить? Почему?
Немного истории…Умножение чисел сейчас начинают изучают во втором классе школы. А вот в XVIII-XIX веках совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения.
А вот в XVIII-XIX веках совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения.
Однако в России среди крестьян некоторых губерний был распространен способ, который не требовал знания всей таблицы умножения. Он получил название “русский, крестьянский способ умножения”. Здесь необходимо было лишь умение умножать и делить числа на 2.
Русский, крестьянский способ умножения (алгоритм).
ВИДЕО ИЗ ИНТЕРНЕТА
Мы видим перед собой НИЗМЕННОСТЬ ПРИМЕНЕНИЯ ЗНАНИЙ
Первичное закрепление с комментированием
РАБОТА ПО УЧЕБНИКУ С. 62, №1
Физкультурная минутка из интернета
А сейчас выполним задание из учебника на стр. 62 №2, №3
Физминутка для глаз
Отдыхаем мы с умом Петуха мы соберём. (танграм)
Самостоятельная работа
№6 1 вариант — верхние
2 вариант — нижние
Мы пришли к ОВРАГУ ДОМАШНИХ ЗАДАНИЙ.
Я всё понял, но у меня остались вопросы. МЕСЯЦ
МЕСЯЦ
Я всё понял, могу работать по алгоритму. ЗВЕЗДОЧКУ
Я всё понял, могу работать по алгоритму, могу объяснить другому. СОЛНЫШКО.
-Если вы согласны с первым утверждением, нарисуйте…
Тем, кто нарисовал месяц: предлагаю выполнить №1 в р/т, выучить алгоритм умножения столбиком на стр. 62 учебника
Тем, кто нарисовал звездочку: предлагаю выполнить задания в р/т стр. 56
Тем, кто нарисовал солнышко: предлагаю выполнить задания в р/т стр. 56 — 57
Пришла пора подвести итог урока, тем более, что мы с вами на последнем участке нашего путешествия
НИЗИНЕ ИТОГА УРОКА.
Да, пришла пора подвести итоги.
Какой приём умножения мы повторяли на уроке?
Расскажите алгоритм письменного умножения на двузначное число.
— Какие факты из истории математики вам понравились?
— Как вы думаете, ваши родители умеют умножать числа “русским, крестьянским способом умножения”?
Посмотрите на свои листы самооценки и оцените свою работу на уроке.
Я довольна вашей работой на уроке. Поставить оценки.
А оценка всему классу: МОЛОДЦЫ!
— Где вам пригодятся знания, полученные на уроке?
Рефлексия учебной деятельности
— Ну, а сейчас прошу вас высказаться по уроку по привычной для нас схеме:
1. На уроке я узнал…
2. Я научился…
3. На уроке я работал …
4. Своей работой на уроке я …
5. Урок для меня показался …
6. Мое настроение …
7. Материал урока мне был…
Я надеюсь, что вы не утратите интереса, а напротив, будете стремиться к знаниям более глубоким, и не только на уроках математики, но и на других уроках, чтобы войти во взрослую жизнь грамотными и активными.
Спасибо за урок!
Частичные продукты: определение, методы и примеры
Что такое частичный продукт? Частичные произведения — отличный способ научиться умножать многозначные числа. Этот пошаговый продукт позволяет учащимся использовать концепцию разрядов и умножать числа. Эта эффективная стратегия умножения улучшает чувство числа. Таким образом, мы учимся выполнять расчеты стратегически, а не запоминать последовательность шагов.
Эта эффективная стратегия умножения улучшает чувство числа. Таким образом, мы учимся выполнять расчеты стратегически, а не запоминать последовательность шагов.
Следующая статья представляет собой частичную математику произведений, шаги для умножения двух- или трехзначных чисел в столбцах. Вы также встретите решенные примеры с пояснениями и практическими задачами, чтобы улучшить свою подготовку.
Частичное произведение — это произведение, полученное при умножении множимого на одну цифру множителя, имеющего более одной цифры.
Разбиваем число на части для умножения. Затем мы умножаем части по отдельности, а затем складываем их вместе.
Умножение частичных произведений
Следующий пример поможет вам понять концепцию умножения частичных произведений.
| 4 8 × 6 Чтобы умножить 6 × 48, используя понятия частичных произведений, мы будем умножать его по частям. Итак, сначала напишем числа друг под другом.  | 4 8 × 6 4 8 We will begin by multiplying 6 and 8, and we will write down the answer completely, i.e., 48. | 4 8 × 6 4 8 2 4 0 Затем умножим 6 × 40 и запишем произведение под 48. Здесь надо отметить, что «4» в числе 48, это десятки место. Итак, 4 означает 40. | 4 8 × 64 8+ 2 4 02 8 8 Наконец, мы сложим два произведения. |
Итак, шаги для умножения частичного произведения с однозначными числами следующие:
- Сначала запишем два числа под другим.
- Мы начнем с умножения одной цифры второго числа на одну цифру первого числа. Мы запишем товар.
- Далее мы умножим одну цифру второго числа на цифру десятков первого числа и запишем произведение под первым произведением.

- Здесь мы должны иметь в виду, что в разряде десятков помимо написанного числа будет стоять ноль. Например, если число 36 и 3 стоят в разряде десятков, то мы должны отметить, что 3 означает 30. Расширенная форма 36 = 30 + 6.
- Наконец, мы сложим два частичных произведения, чтобы получить окончательный ответ.
Умножение частичных произведений с трехзначными числами
В предыдущем примере мы узнали, как умножать двузначные числа, используя концепцию частичных произведений. Вот как умножать трехзначные числа с помощью умножения частичных произведений.
| 2 8 4 × 2 Чтобы умножить 284 × 2, используя концепцию частичного произведения, мы будем умножать его по частям. Итак, сначала напишем числа друг под другом. | 2 8 4 × 2 8 We will begin by multiplying 2 × 4, and we will write down the answer, i.  e., 8. e., 8. | 2 8 4 × 2 8 1 6 0 Тогда умножим 2 × 80 и запишем произведение под цифрой 8. Здесь надо учесть, что «8» в числе 284 стоит в разряде десятков. Итак, 8 означает 80. | 2 8 4 × 2 81 6 0+4 0 05 6 8Далее мы умножим 2 × 200 и запишем произведение под 160. Здесь разрядное значение 2 в числе 284 будет 200. Наконец, мы сложим три частичных произведения. |
Частичные произведения двузначных множителей
До сих пор мы видели примеры частичных произведений для одноразрядных множителей. Что происходит, когда у нас есть числа, в которых множитель имеет более одной цифры. Рассмотрим следующий пример, чтобы понять концепцию умножения частичных произведений для многоразрядных множителей и множителей.
| 8 4 × 2 1 Чтобы умножить 84 × 21, используя концепцию частичного произведения, мы будем умножать его по частям.  Итак, сначала напишем числа друг под другом. Итак, сначала напишем числа друг под другом. | 8 4 × 2 1 4 Мы начнем с умножения 1 × 4, и мы запишем ответ, т.е. 4. | 8 20202020202020202020 4 4 4 4 4 4 4 4 | 8 20202020202020202 × 2 1 4 8 0 Затем мы умножим 1 × 80 и запишем произведение под цифрой 4. Здесь мы должны отметить, что «8» в числе 84 стоит в разряде десятков. Итак, 8 означает 80. | 8 4 × 2 1 48 08 0 8 4 × 2 1 48 08 0+1 6 0 01 7 6 4Далее умножим 20 × 4 и запишем произведение под 80.  Здесь разрядное значение 2 в числе 21 будет 20. Наконец, мы умножим 20 на 80 и запишем произведение меньше 80. Сложите четыре частичных произведения, чтобы получить ответ. Здесь разрядное значение 2 в числе 21 будет 20. Наконец, мы умножим 20 на 80 и запишем произведение меньше 80. Сложите четыре частичных произведения, чтобы получить ответ. |
Итак, шаги для умножения частичных произведений с двузначными числами следующие:
- Сначала запишем два числа, одно под другим.
- Мы начнем с умножения одной цифры второго числа на одну цифру первого числа. Мы запишем товар.
- Далее мы умножим одну цифру второго числа на цифру десятков первого числа и запишем произведение под первым произведением.
- Мы должны принять во внимание, что разряд десятков будет иметь ноль в дополнение к числу, записанному с учетом его разрядности. Например, если число 26 и 2 стоят в разряде десятков, то мы должны отметить, что 2 означает 20. Расширенная форма 26 = 20 + 6.
- Далее мы умножаем разряд десятков множителя на разряд единиц множимого. Мы напишем частичное произведение ниже двух частичных произведений.

- Наконец, мы умножим разряд десятков множителя на разряд десятков множимого и запишем его под предыдущими тремя частичными произведениями.
- Мы сложим четыре частичных произведения, чтобы получить окончательный ответ.
Образец словесной задачи
Пример: Длина прямоугольника 23 метра. Ширина прямоугольника 12 метров. Чему равна площадь прямоугольника?
Решение: Площадь прямоугольника = длина прямоугольника × ширина прямоугольника
Итак, мы должны умножить 23 × 12.
| 2 3 × 1 26 | 2 1 26 | 2 1 26 | 2 1 26 | 2 1 26 | 1 26 | 1 26 | 3 × 1 2 6 4 0 | 2 3× 1 2 44 03 00023 | 2 3 × 1 2 44 03 0+2 0 0 2 7 4 |
Разделение частичных произведений
Деление частичных произведений аналогично умножению частичных произведений.
Этот метод также называется методом деления на частные, так как мы получаем частное по частям. Складываем части, чтобы получить окончательный ответ.
Следующий пример частичного разделения продуктов поможет вам понять принцип разделения.
Пример: Разделить 960 на 6
Шаги для частичного деления продуктов :
- Мы начнем с вычисления чисел, с которыми легко работать, например, кратных 10, 100 и т. д. Итак, умножим 6 на 100 и запишем произведение под делимым.
- Вычесть произведение из делимого. Итак, из 960 отнимем 600, и останется 360.
- Теперь найдем другой номер и повторим шаги. На этот раз мы умножим 6 на 20.
- Снова вычтем 120 из 360, и у нас останется 240.

- Теперь, когда у нас есть 240, мы можем умножить 6 на 40. Получится 240.
- Вычтите два, и останется ноль.
- Наконец, мы сложим все частные, т. е. 100 + 20 + 40 = 160.
- Ответом будет сумма частных.
Практические задачи
Вопрос 1 : Умножьте следующие двузначные числа:
- 23 × 3
- 45 × 9
Вопрос 2 : Умножьте следующие трехзначные числа:
- 123 × 4
- 897 × 8
Вопрос 3 : Умножьте следующие четырехзначные числа:
- 5798 × 6
- 2378 × 9
Вопрос 4 : Умножьте следующие числа:
- 56 × 78
- 12 × 44
- 567 × 12
- 45 × 121
Вопрос 5 : Эмма купила младшему брату 25 ручек. Стоимость каждой ручки составляла 5 долларов. Найдите общую стоимость ручек, используя метод умножения частичных произведений.
Вопрос 6 : В классе 40 учеников, и Лили нужно раздать 560 конфет. Сколько шоколадок получит каждый ученик? Используйте метод частичного деления продуктов.
Умножение чисел с использованием разрядного значения (определение, типы и примеры)
Содержание
- Что такое разрядное значение?
- Использование значения места при умножении
- Использование значения места для умножения на 10, 100, или 1000
- Правила для умножения с 10, 100 или 1000
- Факты о умножении
- Решенные примеры
- Часто задаваемые вопросы
Что такое разрядное значение?
Разрядное значение — это значение позиции каждой цифры в числе.
Рассмотрим, например, число 242.
Разрядное значение цифры 2 на месте единиц равно 2 × 1 = 2 или 2 единицы.
Разрядное значение цифры 4 в разряде десятков равно 4 × 10 = 40 или 4 десятка.
Точно так же разрядное значение цифры 2 в сотых долях равно 2 × 100 = 200 или 2 сотых.
Использование разрядного значения при умножении
При умножении двух чисел учитывается разрядное значение каждой цифры в числах и выполняется индивидуальное умножение.
Позже результаты отдельных умножений складываются, чтобы получить окончательный результат.
Давайте воспользуемся разрядным значением для вычисления 15 × 5. Мы нарисуем диаграмму разрядного значения для выполнения умножения.
\(\Стрелка вправо\)( 5 × 5) + (5 × 10)
= 25 + 50
= 75
Это можно представить в виде столбца следующим образом:
(i) Цифра в разряде единиц во втором числе умножается на цифру в разряде единиц в первом числе.
(5 × 5) = 25 (Умножьте 5 и 5)
(ii) Цифра, стоящая на месте единиц во втором числе, умножается на цифру на месте десятков в первом числе.
5 × 10 = 50 (Умножьте 5 на 10)
10 × 10
(iii) Затем результаты обоих шагов складываются для получения окончательного результата.
25 + 50 = 75 (Добавить)
Аналогичные шаги будут предприняты для умножения чисел, имеющих цифры в разряде сотен или тысяч.
Использование разрядного числа для умножения на 10, 100 или 1000
Это простое применение умножения с разрядным значением, в котором мы упрощаем умножение, выражая числа, которые нужно умножить, через десятки, сотни или тысячи и позже выполните стандартное умножение.
Рассмотрим следующее умножение:
7 × 10 (здесь 10 можно записать как 1 десяток)
= 7 × 1 десяток
= 7 десятков
= 70
Рассмотрим другой пример:
9 × 200 (здесь 200 можно записать как 2 сотни)
9 × 2 сотни
= 18 сотен
= 1800
2
Правила для умножения, 100002
Ниже приведены основные правила, которым необходимо следовать при умножении любых ненулевых чисел на 10, 100 или 1000.
- При умножении любого ненулевого числа на 10 просто добавьте ноль в конце этого числа.

Например:
5 × 10 = 50 - При умножении любого ненулевого числа на 100 просто добавьте два нуля в конце этого числа. Например:
5 × 100 = 500 - При умножении любого ненулевого числа на 1000 просто добавьте три нуля в конце этого числа. конец этого числа.
Например:
2 × 1000 = 2000
Факты о умножении
- Если число умножается на 0, результат равен 0.
10 × 0 = 0 0003
0 × 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0.
112 × 0 = 0
- Если ненулевое число умножить на 10, 100 или 1000 соответственно, произведением будет само число с 1, 2 или 3 нулями в конце соответственно.
- При умножении умножаемое число называется множимым, а число, на которое оно умножается, называется множителем.
Результат умножения называется произведением.
10 × 7 = 70
10 → множимое
7 → множитель
70 → Продукт
- Если число умножить на 1, произведением будет само число.

Решенные примеры
Пример 1:
Найдите произведение для каждого из следующих умножений.
(i) 7 × 3 ________
(ii) 7 × 30 _________
(iii) 7 × 300 _________
(iv) 7 × 3000 __________
Решение:
(I) 70002 . × 3 = 21
(II) 7 × 3 TENS
= 21 TENS
= 210
(III) 7 × 3 Сотни
= 21 Сотни
= 2100
(IV) 7 × 3
= 2100
(IV) 7000
= 2100
(IV) 7 тысяч
= 21 тысяча
= 21000
Пример 2:
Найдите недостающий множитель.
(i) ______× 100 = 600
(ii) 5 ×______ = 50
(iii) 9 × 20 = ______
Решение:
(i) Мы знаем, что
(Множное) × (Множитель) = Произведение
(ii) Мы знаем, что
(Множитель) × (Множитель) = Произведение
5 × _____= 50
Используя правило умножения числа с 10, мы видим, что множитель равен 10.
(III) 9 × 20
= 9 × 2 десяти,
= 18 TENS
= 180
Пример 3:
Управляющий имеет две разновидности глитера. 10 упаковок одного сорта по 5 ручек в каждой и 20 упаковок второго сорта по 7 ручек в каждой. Итак, сколько всего блестящих ручек у продавца?
Решение:
Первая разновидность → 10 × 5 = 50 (Умножить)
Второе разнообразие → 20 × 7 = 140 (умножение)
50 + 140
= 190 [Добавить]
Следовательно, владелец магазин имеет 190 ручек блеска.
Пример 4:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой. У него также есть 5 коробок по 30 шоколадных конфет в каждой.
Сколько всего конфет у Лиама?
Решение:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой.
Общее количество карамельных конфет,
= 2 × 20
= 40 [Умножить]
Всего у Лиама 40 карамельных конфет.
У Лиама также есть 5 коробок по 30 кофейных конфет в каждой.
Общее количество шоколадных конфет,
= 5 × 30
= 150 [Умножить]
Всего у него 150 шоколадных конфет.
Итак, общее количество конфет у Лиама
= 40 + 150
= 190 [Добавить]
Следовательно, всего у Лиама 190 конфет.
Часто задаваемые вопросы
Какое свойство можно использовать для определения произведения числа на 0?
Согласно нулевому свойству умножения, если число умножается на ноль, произведение будет 0.
Что означает разрядное значение цифры в числе?
В математике каждая цифра в числе имеет определенное разрядное значение. Его можно определить как значение цифры в числе на основе ее позиции в числе. Каждое место имеет значение, в 10 раз превышающее значение места справа от него.
Объясните закономерность, наблюдаемую в произведениях числа, умноженного на 10, 100 и 1000 соответственно?
Если любое ненулевое число умножить на 10, 100 или 1000, произведением будет само число, заканчивающееся 1, 2 или 3 нулями соответственно.


 осуществлять выход из затруднительной ситуации
осуществлять выход из затруднительной ситуации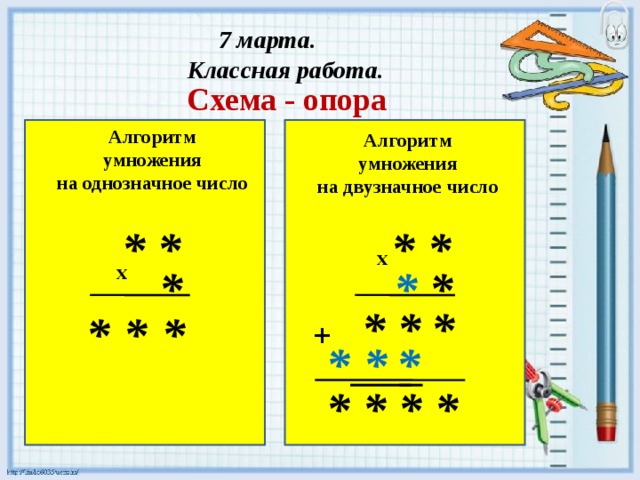
 Реализация построенного проекта в решении примеров, записанных столбиком.
Реализация построенного проекта в решении примеров, записанных столбиком. Умножу первый множитель на число единиц: 34 × 9.
Умножу первый множитель на число единиц: 34 × 9.
 Самостоятельная работа с самопроверкой по эталону.
Самостоятельная работа с самопроверкой по эталону.
 Научиться умножать на двузначное число.)
Научиться умножать на двузначное число.)