Произведение это деление или умножение: Произведение (математика) | это… Что такое Произведение (математика)?

Правила умножения числа на ноль

Всем нам в школе учителя прочно вбили в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!». И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда. Как это сделать? Какие слова подобрать? Будем разбираться.

Содержание:

Правила умножения любого числа на ноль

Что такое ноль

Из истории

Какие действия в математике можно выполнять с нулём

Умножение на ноль, правило математики

Деление на ноль, правило математики

Подведём итоги

Всем нам в школе учителя прочно вбили в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!». И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда.

Как это сделать? Какие слова подобрать? Будем разбираться.

Что такое ноль

Вокруг этой цифры всегда велось много споров. Число 0 занимает особое место в математике, даже несмотря на то, что оно буквально означает «ничто», «пустота». Ноль — это целое число, одна из цифр в десятичной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех цифр, стоящих левее, на разряд — десяток, сотню и так далее. Например, если рядом с 5 ставим 0, получаем 50, если рядом с 50 ставим 0, получаем 500. А ещё ноль — это число, отделяющее положительные цифры от отрицательных на числовой прямой. Сам ноль при этом знака + / — не имеет.  

Какие действия в математике можно выполнять с нулём

С нулём выполняются все арифметические действия: сложение, вычитание, умножение, деление, возведение в степень. При выполнении сложения и вычитания с нулём обычно проблем и сложностей не возникает. Здесь всё просто. 

Если к любому числу добавить 0, это означает, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй.

‍

 

‍

То же самое будет, если отнять ноль. 

Если ноль разделить на любое ненулевое число, то в результате тоже получится ноль. 

А вот операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на 0 получается 0. Именно умножение на ноль мы сейчас рассмотрим подробнее, так как в нём содержатся некоторые нюансы. А заодно поговорим немного и о делении на ноль.

Умножение на ноль, правило математики

Чтобы разобраться, чем отличается умножение числа на ноль от умножения других чисел друг на друга, нужно для начала понять определение умножения в целом. Умножение — одно из основных действий в математике. Умножение — это арифметическое действие, когда сложение одинаковых чисел происходит искомое количество раз. В этом действии участвуют два составляющих компонента — множимое и множитель. Результат их умножения называют произведением. То есть для натуральных чисел умножением, по сути, является многократное сложение. Таким образом, чтобы умножить число a на число b, необходимо b раз сложить a.        

                            a ⋅ b = a + a + … + a} b

Так, пример 4 х 3 = 12 можно заменить следующим выражением: 4 + 4 + 4 = 12. То есть число 4 было взято 3 раза. 

А можно ли умножать на ноль? Можно, только это бессмысленно и бесполезно. Ведь ноль — это ничто, пустота. А какой смысл умножать на пустоту? Тут, как ни крути, всё равно будет получаться ноль. 

Как на примере объяснить это правило детям? Попробуем вот так:

‍

• если съесть пять раз по два яблока, получится 2 * 5 = 2 + 2 + 2 + 2 + 2 = 10, то есть в итоге будет съедено 10 яблок;
• если съесть по два яблока трижды, получится 2 * 3 = 2 + 2 + 2 = 6, в итоге будет съедено 6 яблок;
• если съесть по два яблока ноль раз, то 2 * 0 = 0 * 2 = 0 + 0 = 0, в итоге не съедено ни одного яблока.

Ведь съесть ноль раз — это означает не съесть ни одного. Ноль — это ничего, а когда у вас нет ничего, то на сколько его ни умножай, всё равно будет ноль.

Правда, иногда выдвигаются следующие возражения: предположим, у человека в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся у него в руке. Почему же тогда результат равен нулю? Да, яблоки действительно из руки никуда не денутся. Но ведь в примере мы считаем именно съеденные яблоки, то есть те из них, которые были съедены, проще говоря, оказались в желудке человека. А в последнем случае они туда не попали. Поэтому человек съел ноль яблок. 

Итак, основное правило гласит: при умножении числа на ноль и при умножении нуля на число в ответе всегда будет получаться ноль.

a ⋅ 0 = 0

0 ⋅ a = 0

Это правило умножения на ноль в математике действительно для любых чисел: положительных, отрицательных, целых, дробей, разрядных, рациональных, иррациональных. В любом случае произведение будет нулевым.

Для лучшего запоминания правила приведём примеры умножения на ноль:

0 ⋅ 3 = 0 + 0 + 0 = 0

0 ⋅ 4 = 0 + 0 + 0 + 0 = 0

756 ⋅ 0 = 0

293 ⋅ 0 = 0

Деление на ноль, правило математики

А что же с делением на 0? Мы со школы помним правило: на ноль делить нельзя. Все это заучивают, не требуя лишних доказательств. Нельзя так нельзя. Большинство людей действительно не делит на ноль только исходя из этого правила, не пытаясь найти ответ, по которому станет понятен этот запрет. А почему, собственно, нельзя? 

Деление в математике — действие, обратное умножению, также состоящее из двух компонентов — делимого и делителя. Результат деления называют частным. Также иногда результат деления называют отношением. Если умножение для натуральных чисел заменяет многократное сложение, то, соответственно, деление будет заменять многократное вычитание.

Чтобы было понятнее, рассмотрим на примерах.

• Разделим число 8 на число 2 (8 : 2). Из действия вычитания мы находим, что число 2 содержится в 8 четыре раза. В данном случае 8 — делимое, 2 — делитель, 4 — частное.
• Теперь разделим 0 на 2 (0 : 2). Чтобы 0 разделить на 2, надо найти число, при умножении которого на 2 получится 0. Это ноль, так как 0 ⋅ 2 = 0. Значит, 0 ⋅ 2 = 0. При делении нуля на любое число, не равное нулю, частное равно нулю. 
• А теперь попробуем разделить 4 на 0 (4 : 0). Данное выражение можно представить и в виде уравнения: 0 ⋅ x = 4. Следовательно, чтобы разделить 4 на ноль, необходимо найти такое число, при умножении на которое получится 4, а это невозможно исходя из того, что мы выяснили ранее.

Следовательно, делить на 0 нельзя, так как такого числа, при умножении которого на ноль получится 4, не существует. И всё-таки лучше всего это правило просто запомнить и никогда не нарушать. Для лучшего запоминания предложите своему ребёнку выучить небольшое стихотворение:

Расскажу тебе, позволь, 

Чтобы не делил на 0! 

Режь 1, как хочешь, вдоль, 

Только не дели на 0!

Таким образом, с нулём возможно совершать любые арифметические действия: прибавлять и вычитать любые числа, умножать на значения, не равные нулю, возводить в степень, не равную нулю. Единственное ограничение — ноль не может быть делителем для любого действительного числа. В арифметике подобные действия считаются невозможными и бессмысленными.

Подведём итоги

Итак, сегодня мы выяснили, что за цифра такая — ноль. Мы узнали историю её возникновения. А также разобрались, чем отличается умножение числа на 0 от умножения других чисел друг на друга, а также почему на ноль нельзя делить. Чтобы закрепить полученные новые знания, важно отработать их на практике. Поэтому для закрепления и лучшего запоминания предложите своему ребёнку решить примеры:

7 * 0 

15 * 0

0 * 9

0 * 346

72 : 9 * 0

Конечно же, во всех этих примерах ответ будет 0:

7 * 0 = 0

15 * 0 = 0

0 * 9 = 0

0 * 346 = 0

72 : 9 * 0 = 0

Закрепляем тему «Умножение на ноль»

Закрепить эту и многие другие изученные темы по математике можно на образовательной платформе iSmart. С помощью онлайн-тренажёров дети в  увлекательной форме наработают вычислительную беглость в решении примеров с умножением на ноль.  

Вот так, например, выглядят задания для второго класса:

А так выглядит сам каталог заданий по математике образовательной платформы iSmart: 

Образовательная платформа iSmart разработана учителями и специалистами в области детской психологии в соответствии с требованиями ФГОС. Она предлагает программы подготовки по всем изучаемым в школе предметам, пакеты заданий для подготовки к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Регистрируйте своего ребёнка и начинайте заниматься прямо сейчас!

‍

3. Умножение и деление натуральных чисел

п1. Умножение натуральных чисел и его свойства

Умножить число m на натуральное число n  — значит найти сумму n слагаемых, каждое из которых равно m.

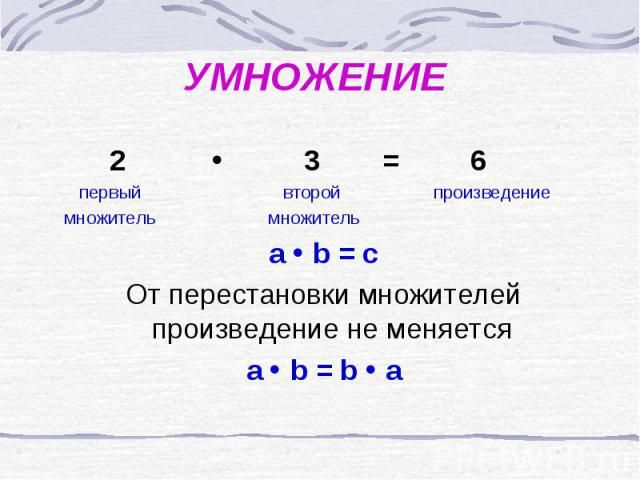
Выражение m·n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.

Свойства умножения: 

1. Переместительное свойство умножения: Произведение двух чисел не изменяется при перестановке множителей: a · b = b · а
2. Сочетательное свойство умножения: Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель:
   a · (b · с) = (а · b) · c.
3. Свойство умножения на единицу: Сумма n слагаемых, каждое из которых равно 1, равна n: 1 · n = n.
4. Свойство умножения на ноль: Сумма n слагаемых, каждое из которых равно нулю, равна нулю: 0 · n = 0.

Знак умножения можно опускать: 8 · х = 8х, или а · b = ab, или a · (b + с) = a(b + с)

п2. Деление

Действие, по которому по произведению и одному из множителей находят другой множитель, называют делением.  

Число, которое делят, называют делимым; число, на которое делят, называют делителем, результат деления называют частным.

Частное показывает, во сколько раз делимое больше, чем делитель.

На нуль делить нельзя!

Свойства деления: 

1. При делении любого числа на 1 получается это же число: а : 1 = а.
2. При делении числа на это же число, получается единица: а : а = 1.
3. При делении нуля на число получается нуль: 0 : а = 0.

Чтобы найти неизвестный множитель, надо произведение разделит на другой множитель. 5х = 45 х  = 45 : 5 х = 9 Чтобы найти неизвестное делимое, надо частное умножить на делитель.  х : 15 = 3 х = 3 · 15 х = 45

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

48 : х = 4 х = 48 : 4

х = 12

п3. Деление с остатком

Остаток всегда меньше делителя.

Здесь число 23 – делимое, 4 – делитель, 5 – неполное частное и 3 – остаток.

Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка или, иначе, нацело.

Чтобы найти делимое a при делении с остатком, надо умножить неполное частное  с на делитель b и к полученному произведению прибавить остаток d.  а = с · b + d

п4. Упрощение выражений

Свойства умножения:

1. Распределительное свойство    умножения относительно      сложения: Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения: (а + b)с = ас + bc.
2. Распределительное свойство умножения относительно вычитания
   : Чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе: (а — b)с = ас — bc.

3а + 7а = (3 + 7)а = 10а

Решить уравнение: 

3у + 7у + 25 = 85

(3 + 7)у + 25 = 85

10у + 25 = 85

10у  = 85 – 25

10у = 60

у = 60 : 10

у = 6

п5. Порядок выполнения действий

Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.

Правила порядка выполнения действий:

1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Каждое выражение задает программу своего вычисления. Она состоит из команд.

 

п6. Квадрат и куб

Произведение, в котором все множители равны друг другу, записывают короче: 

а · а · а · а · а · а = а⁶

Читают: а в шестой степени. Число а называют основанием степени, число 6 – показателем степени, а выражение  а⁶ — называют степенью.

Произведение n и n называют квадратом числа n и обозначают n² (эн в квадрате):  n² = n · n

Таблица квадратов:

n	1	2	3	4	5	6	7	8	9	10
n2	1	4	9	16	25	36	49	64	81	100

 

n	11	12	13	14	15	16	17	18	19	20
n2	121	144	169	196	225	256	289	324	361	400
Произведение n · n · n называют кубом числа n и обозначают n3 (эн в кубе):  n3 = n · n · n Таблица кубов:
n	1	2	3	4	5	6	7	8	9	10
n3	1	8	27	64	125	216	343	512	729	1000

 

Первая степень числа равна самому числу.

Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения

остальных действий.

Что означает произведение слов в математике?

Обновлено 19 декабря 2020 г.

Автор: Берт Маркграф

Произведение — это результат выполнения математической операции умножения. Когда вы перемножаете числа вместе, вы получаете их произведение. Другими основными арифметическими операциями являются сложение, вычитание и деление, а их результаты называются соответственно суммой, разностью и частным. Каждая операция также имеет специальные свойства, определяющие порядок расположения и комбинирования чисел. Для умножения важно знать об этих свойствах, чтобы вы могли умножать числа и комбинировать умножение с другими операциями, чтобы получить правильный ответ.

TL;DR (слишком длинно, не читал)

Значение произведения в математике — это результат умножения двух или более чисел. Чтобы получить правильный продукт, важны следующие свойства:

• Порядок чисел не имеет значения.
• Группировка чисел скобками не действует.
• Умножение двух чисел на множитель и последующее сложение их равносильно умножению их суммы на множитель.
• Умножение на 1 оставляет число без изменений.
  

Значение произведения числа

Произведение числа на одно или несколько других чисел — это значение, полученное при умножении чисел. Например, произведение 2, 5 и 7 равно

2 × 5 × 7 = 70

Хотя произведение, полученное путем умножения определенных чисел, всегда одно и то же, произведения не уникальны. Произведение 6 и 4 всегда равно 24, как и произведение 2 и 12 или 8 и 3. Независимо от того, какие числа вы умножаете, чтобы получить произведение, операция умножения имеет четыре свойства, которые отличают ее от других основных арифметических операций. , Сложение, вычитание и деление имеют некоторые из этих свойств, но каждое из них имеет уникальную комбинацию.

Арифметическое свойство коммутации

Коммутация означает, что условия операции можно менять местами, и последовательность чисел не влияет на ответ. Когда вы получаете произведение путем умножения, порядок, в котором вы умножаете числа, не имеет значения. То же самое и с дополнением. Вы можете умножить 8 × 2, чтобы получить 16, и вы получите тот же ответ, если 2 × 8. Аналогично, 8 + 2 дает 10, тот же ответ, что и 2 + 8.

Вычитание и деление не обладают свойством коммутация. Если вы измените порядок чисел, вы получите другой ответ. Например,

8 ÷ 2 = 4 \text{ но } 2 ÷ 8 = 0,25

Для вычитания

8 — 2 = 6 \text{ но } 2 — 8 = -6

Деление и вычитание не являются коммутативными операциями.

Распределительное свойство

Распределение в математике означает, что умножение суммы на множитель дает тот же ответ, что и умножение отдельных чисел суммы на множитель с последующим сложением. Например,

3 × (4 + 2) = 18 \text{, и } (3 × 4) + (3 × 2) = 18

Сложение перед умножением дает тот же ответ, что и распределение множителя между числами, которые нужно сложить, и затем умножение перед сложением.

Деление и вычитание не обладают распределительным свойством. Например,

3 ÷ (4 — 2) = 1,5 \текст{ но } (3 ÷ 4) — (3 ÷ 2) = -0,75

Вычитание перед делением дает другой ответ, чем деление перед вычитанием.

Свойство ассоциативности для произведений и сумм

Свойство ассоциативности означает, что если вы выполняете арифметическую операцию более чем с двумя числами, вы можете связать два числа или заключить их в скобки, не влияя на ответ. Произведения и суммы обладают свойством ассоциативности, а разности и частные — нет.

Например, если произвести арифметическую операцию над числами 12, 4 и 2, то сумма может быть рассчитана как

(12 + 4) + 2 = 18 \text{ или } 12 + (4 + 2) = 18

Пример произведения:

(12 × 4) × 2 = 96 \text{ или } 12 × (4 × 2) = 96

Но для частных

\frac{12 ÷ 4}{2} = 1. 5 \text{ while } \frac{12}{4 ÷ 2} = 6

и для разностей

(12 — 4) — 2 = 6 \text{ while } 12 — (4 — 2) = 10

Умножение и сложение обладают ассоциативным свойством, а деление и вычитание — нет.

Операционные тождества — разница и сумма по сравнению с произведением и частным

Если вы выполняете арифметическую операцию над числом и операционным тождеством, число остается неизменным. Все четыре основные арифметические операции тождественны, но не совпадают. Для вычитания и сложения идентичность равна нулю. Для умножения и деления тождество одно.

Например, для разницы 8 − 0 = 8. Число остается одинаковым. То же самое верно для суммы 8 + 0 = 8. Для произведения 8 × 1 = 8 и для частного 8 ÷ 1 = 8. Произведения и суммы имеют одинаковые основные свойства, за исключением того, что они имеют разные операционные тождества. В результате умножение и его произведения обладают уникальным набором свойств, которые необходимо знать, чтобы получить правильные ответы.

Сложение, вычитание, умножение и деление (видео и практика)

TranscriptPractice

Привет, ребята! Сегодня мы рассмотрим математические операции: сложение , вычитание , умножение и деление . Эти четыре операции служат фундаментальными строительными блоками для всей математики, поэтому крайне важно иметь четкое представление о том, на чем можно основываться. Давайте углубимся.

Сложение и вычитание

Мы используем сложение и вычитание для решения многих реальных ситуаций. Сложение и вычитание — это просто математические термины, используемые для описания «объединения» и «удаления». Когда мы добавляем , мы объединяем или увеличиваем. Когда мы вычитаем , мы отнимаем или уменьшаем.

Напоминаем:

• Для сложения используется символ \(+\)
• Ответ на задачу на сложение называется суммой
• Для вычитания используется символ \(–\)
• Ответ на задачу на вычитание называется разностью

 
По сути, сложение и вычитание — противоположные операции. Один добавляет стоимость, а другой вычитает стоимость. Одна из стратегий визуализации этих двух операций — использование числовой прямой. Мы будем использовать числовую прямую, чтобы проиллюстрировать следующие примеры.

Давайте представим ситуацию, связанную с продажей попкорна. Для этого сценария предположим, что вы пытаетесь собрать деньги, продавая пакеты с попкорном, и вы начинаете с 20 пакетов.

Когда придет ваш первый покупатель, он захочет купить 4 пакета попкорна. Это означает, что ваше оставшееся количество сумок уменьшится. Мы можем представить эту ситуацию с помощью простого уравнения, включающего вычитание. Мы начали с 20 мешков и «уменьшили на 4» или вычли 4. Наше уравнение вычитания записывается как \(20-4=16\).

На числовой прямой мы можем представить это вычитание, начав с 20 и затем переместившись на четыре единицы назад в отрицательном направлении. Каждый прыжок назад представляет собой вычитание на 1.

Предположим, вы начали с 20 пакетов попкорна, а к концу дня у вас осталось 6 пакетов. Вам нужно пополнить свой запас, чтобы поддерживать продажи, поэтому вы делаете еще 4 пакета попкорна. Сколько пакетов попкорна у вас сейчас есть в наличии для продажи? Для этого сценария, поскольку мы смотрим на увеличение мешков, мы будем использовать сложение.

Эту ситуацию можно описать уравнением \(6+4=10\). Изначально у вас было 6 мешков, а затем «объединили» это количество еще с 4 мешками. Всего у вас 10 мешков. На числовой прямой сложение представлено скачками вправо в положительном направлении. Каждый прыжок вправо представляет собой добавление одной единицы. Так что в этом примере мы бы начали с 6 и прыгнули бы на 4 единицы вправо. Мы видим, что мы приземлились на 10.

Важно отметить, что при использовании сложения порядок значений не имеет значения. Например, \(10+30\) равносильно \(30+10\). Размещение или расположение значений не влияет на результат. Обе схемы будут равны 40. Однако то же самое не верно для вычитания . Означает ли \(30-10\) то же самое, что и \(10-30\)? Явно нет. Мы видим, что порядок имеет значение при работе с ситуацией, связанной с вычитанием. Технический термин для этого качества известен как 9.0102 коммутативное свойство . По сути, это свойство верно для операций, в которых значения могут перемещаться, «коммутировать», а результат выражения или уравнения не изменится. Коммутативность применима к сложению, но не к вычитанию.

Умножение и деление

Другая операция, которая также обладает свойством коммутативности, — это умножение. Давайте обсудим умножение вместе с делением, как мы делали сложение и вычитание. Умножение и деление похожи на сложение и вычитание тем, что выполняют противоположные функции. Функция умножение предназначено для представления нескольких групп определенного значения, тогда как деление предназначено для демонстрации разделения или подразделения значения на более мелкие группы.

Напоминаем:

• Символ, который мы используем для умножения, это \(\times\)
• Ответ на задачу на умножение называется произведением
• Символ, который мы используем для деления, это \(\div \)
• Ответ на задачу о делении называется числом 9. 0102 частное

 

Умножение — это удобный и быстрый способ показать то, что называется «повторяющимся сложением». Например, если вам нужно заполнить 30 мешков попкорна, а в каждом мешке требуется 60 зерен, может потребоваться несколько часов, чтобы подсчитать, сколько всего зерен вам нужно, просто используя сложение. Более быстрый и эффективный способ сделать это вычисление — использовать повторное сложение. Вместо того, чтобы считать каждое семя независимо, мы сгруппировали их и сложили группы вместе. Тогда расчет будет состоять из 30 групп по 60. Эта группировка с целью повторного сложения является по своей сути процессом умножения. 30 групп по 60 записывается как \(30\х60=1800\). Таким образом, для заполнения 30 мешков попкорна требуется 1800 ядер.

И сложение, и умножение коммутативны, потому что порядок не влияет на ответ. 30 групп по 60 дают тот же результат, что и 60 групп по 30. противоположный. Когда мы используем деление, мы, по сути, делим большую группу на более мелкие подгруппы. В нашем примере с попкорном мы можем использовать деление, чтобы ответить на следующий вопрос:

Сколько пакетов попкорна можно приготовить из 1800 зерен, если в каждом пакете требуется 60 семян?

 

В этой ситуации нам нужно разделить большое значение 1800 на группы по 60. Каждая меньшая подгруппа теперь будет представлять пакет попкорна. 1800, разделенных на группы по 60, представлены как \(1800\div 60\). В данном случае ответ равен 30, значит, из наших 1800 ядер можно приготовить 30 пакетов попкорна. Как видите, деление не является коммутативным, потому что порядок значений играет решающую роль в определении ответа. \(1800\div 60\) — это не то же самое, что \(60\div 1800\).

Хорошо, это все для этого обзора математических операций! Спасибо за просмотр и удачной учебы!

Multiplication Chart & Printables

 

Practice Questions

Question #1:

 
The answer to a subtraction problem is called the …

Difference

Sum

Quotient

Product

Show Ответ:

Ответ:

А — правильный ответ. Поскольку вычитание — это разница между меньшим числом и большим числом, ответ на задачу на вычитание называется разницей.

Скрыть ответ

Вопрос № 2:

 
Какое утверждение верно?

Вычитание и умножение — противоположные действия.

Вычитание и деление — противоположные операции.

Умножение и сложение — противоположные операции.

Умножение и деление — противоположные операции.

Показать ответ

Ответ:

D — правильный ответ. Деление разбивает большую группу на более мелкие подгруппы, а умножение представляет собой многократное сложение меньших подгрупп, чтобы найти общее количество в большой группе. Следовательно, эти операции выполняют противоположные функции.

Скрыть ответ

Вопрос № 3:

 
Джейми арендует велосипед за 8 долларов в час. Всего у него велосипед на 4 часа. Какое уравнение можно использовать, чтобы узнать, сколько денег Джейми тратит на аренду велосипеда?

\(8+4=12\)

\(8-4=4\)

\(8\times4=32\)

\(8÷4=2\)

Показать ответ

Ответ:

C — правильный ответ. Поскольку Джейми тратит 8 долларов за каждый час пользования велосипедом, он тратит 8 долларов + 8 долларов + 8 долларов + 8 долларов, что равно 8 долларов ✕ 4, или 32 доллара.

Скрыть ответ

Вопрос № 4:

 
Какое утверждение лучше всего иллюстрирует свойство коммутативности?

\(12÷3=3÷12\)

\(12\times3=3\times12\)

\(12-3=3-12\)

\(12+3=15\)

Показать ответ

Ответ:

B — правильный ответ. Свойство коммутативности гласит, что числа в математической задаче можно перемещать или менять местами, и результат уравнения не изменится. Коммутативное свойство применяется к сложению и умножению, но не работает для деления или вычитания.

Скрыть ответ

Вопрос № 5:

 
В Mike’s Deli индейка стоит 4 доллара за фунт. Кейт покупает индейку, чтобы приготовить бутерброды на обед. Если Кейт тратит 80 долларов, какое уравнение показывает, сколько фунтов индейки она купила?

\(80+4=84\)

\(4÷80=20\)

\(80÷4=20\)

\(80-4=76\)

Показать ответ

Ответ:

C — правильный ответ. Кейт знает, что общая потраченная сумма составила 80 долларов. Она также знает, что каждый фунт стоил ей 4 доллара. Кате нужно знать, на сколько равных групп разбито 80 долларов, если в каждой группе по 4 доллара.