Вычитаем и складываем. Знакомство с составом числа, примеры и задачи — МНОГОКНИГ.ee
Вычитаем и складываем. Знакомство с составом числа, примеры и задачи — МНОГОКНИГ.ee — Книжный интернет-магазинкатегории
книги
НовинкиАкции %АвтомобилиДетективы, боевикиДетская литератураДом, быт, досугИностранные языки, словариИстория, политикаКниги на английском языкеКниги на украинском языкеКомпьютерные технологииЛюбовный романМедицина и здоровьеПодарочные изданияПсихология, философияПутеводители, атласыСовременная и классическая литератураСпорт, оружие, рыбалкаСувениры. АксессуарыФантастикаЭзотерика, астрология, магияЭкономическая литература
Подарочные карты
игры, игрушки
MNOGOKNIG Games Игрушки Книги-игры Настольные игры Развивающие игры
товары для малышей
Прорезыватели и пустышки Шезлонги и качели Автокресла Аксессуары для защиты ребенка Вигвам Детская мебель Детская одежда Детские кроватки Кровать для путешествий Купание малыша Матрасы Подушки для беременных Развивающие игрушки для малышей Текстиль Товары для кормления Уход за малышом Ходунки
товары для праздника
Все открытки Карнавальные костюмы, маски и аксессуары Одноразовая посуда Подарочные коробки Подарочные пакеты Свечи Шарики
товары для школы
Бумажная продукция Глобусы Канцелярские товары Папки Пеналы Товары для творчества Школьные ранцы
товары для живописи, рукоделия и хобби
Декорирование Жемчуг эффект для декупажа Живопись Контур по стеклу и керамике Контур по ткани Краски для свечей Маркеры для скетчинга Моделирование Прочее Рукоделие
традиционные товары
Костровые чаши и очаги Матрёшки Платки Самовары Фарфоровые фигурки
другие товары
Аксессуары для девочек Аксессуары для мальчиков Брелки Копилки Товары для пикника Фотоальбомы
издательство
Об издательстве Многоразовые наклейки Настольные игры Рабочие тетради для дошкольников Рабочие тетради для школьников Развивающее лото Раскраски для девочек Раскраски машины и техника Раскрась водой! Учебные пособия для дошкольников
Код: 4607037890633
Купить
Автор:ВК ДАКОТА
Серия: Папка дошкольника
Год издания: 2022
Кол-во страниц: 36
Тип обложки: Мягкая обложка
Формат: 240x175x2 мм
Вес: 60 г.
Возрастные ограничения: 6+
Под заказ
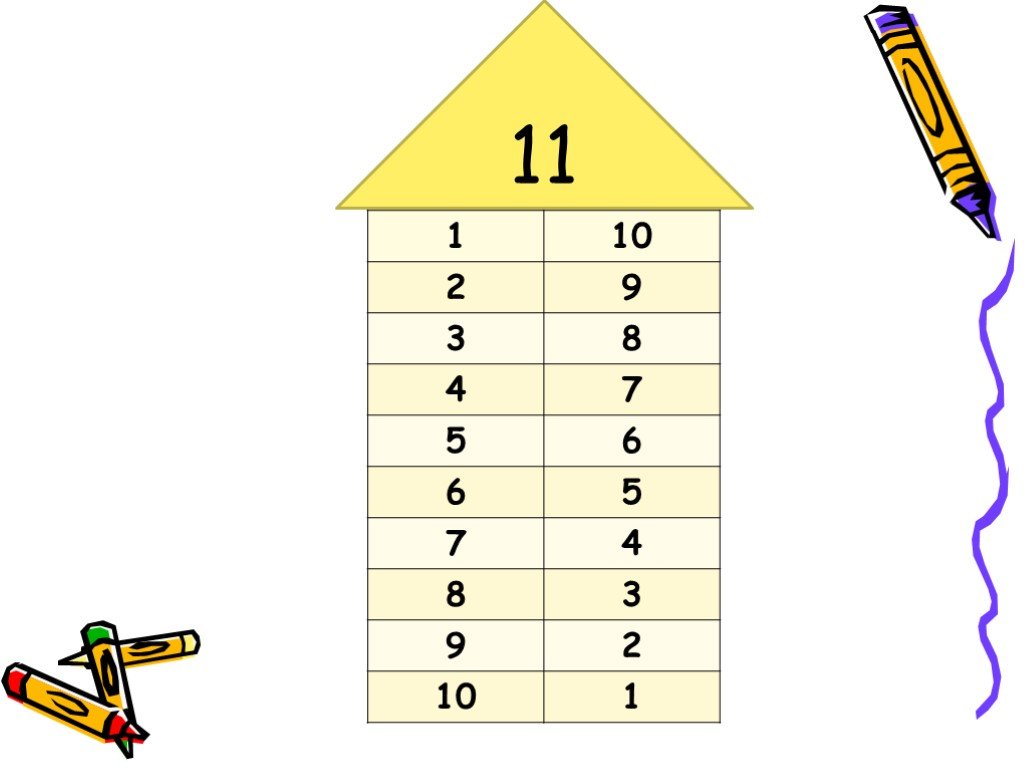
Предлагаем вашему вниманию серию папок для дошкольного образования «Солнечные ступеньки». «Солнечные ступеньки» предназначены для всестороннего развития способностей ребенка. Все задания соответствуют задачам умственного развития и воспитания, определенным «Типовой программой воспитания и обучения в детском саду». Папка дошкольника поможет ребенку: — закрепить состав числа; — сравнивать числа между собой; — решать простые математические задачи на сложение и вычитание. Цветной вкладыш необходимо разрезать по пунктирным линиям. Карточки с цифрами и картинками помогут ребенку самостоятельно составлять различные примеры и задачи.
Конспект урока по математике 1 класс «Состав числа 8»
Урок математики (1 класс)
УМК: «Планета Знаний».
Тема: «Состав числа 8».
Цель урока: Формирование представлений о составе числа 8.
Задачи:
Формирование умений сложения и вычитания чисел на основе знания состава числа 8
развивать навыки устного счёта;
логическое мышление, математическую речь, умение объяснять и доказывать;
воспитывать любознательность, интерес к предмету.
воспитывать уважение друг к другу, формировать умение слушать каждого.
Тип урока: изучение нового.
Планируемые результаты обучения:
Предметные: познакомятся с составом числа 8, научатся выполнять сложение чисел на основе знания состава числа 8, сравнивать примеры на сложение в столбике, выполнять прямой и обратный счет в пределах первого десятка, распознавать геометрические фигуры.
Метапредметные
-Познавательные: сравнивать математические объекты (числа, геометрические фигуры), осуществлять сложение и вычитание чисел на основе знания состава чисел, осуществлять синтез как составление целого из частей
-Регулятивные: планировать свои действия в соответствии с поставленной задачей, развивать умение анализировать, делать выводы
-Коммуникативные: отвечать на вопросы учителя, выражать мысли в устной форме, слушать, дополнять других, доказывать своё мнение, сотрудничать с товарищем при выполнении задания в паре, осуществлять взаимопроверку, обсуждать совместное решение, проявлять уважительное отношение к собеседнику
Личностные: формировать внимательность, мотивацию, саморазвитие, самосовершенствование, положительное отношение к предмету
Виды деятельности: работа фронтальная, индивидуальная, в парах
Этап урока | Содержание деятельности учителя | Содержание деятельности учащихся |
Актуализация опорных знаний 2. 3.Открытие нового знания 4.Закрепление изученного материала 5. Рефлексия | 1.Записан числовой ряд 1 4 2 3 5 6 9 7 8 10 Верните числа на своё место. Назовите четные и нечетные числа, назовите «соседей» числа 6, 8, 3, 9. 2.Продолжите узор нужным фрагментом Молодцы! -Отгадайте загадку. Симпатичный он на вид, Хоть бывает ядовит! У моллюска – 8 ног Он придонный …. -Верно. На слайде изображение осьминога. Рассмотрите картинку. Почему к нам на урок пожаловал осьминог? -Сформулируйте тему урока. -Предположите, что мы сегодня узнаем на уроке? -Рассмотрите рисунок на с.88 №1 Сколько осьминогов на рисунке? Что могут означать равенства: 1+7=8 2+6=8 3+5=8 4+4=8 -Продолжаем работать с учебником №2 Каждая картинка изображает число 8. -Выполните задание в рабочей тетради с.51 №4 Как разделить фигуру из 8 клеток на 2 части? Раскрась в тетради 8 клеток в 2 цвета по-разному. Составь 4 равенства к каждому рисунку. Запиши их. -Выполните вычитание из числа 8, используя сложение. Если трудно, найди в рамке равенства, которые помогут тебе выполнить вычитание. Объясни свой выбор. -Сейчас вы работаете в парах. У вас на столе 3 коробочка и 8 спичек. Разложите 8 спичек по 3 коробочкам разными способами и запишите примеры. -Вспомните, пожалуйста, что такое числовой луч? -Рассмотрите числовой луч №4 с.89 Кто изображен на луче? — От Русалки до Московского Царя 6м. От краба до Морского царя 2м. Покажи на числовом луче, где может находиться краб. Какое расстояние от краба до Русалки? Молодцы! -Работа с математическим веером. -Покажите как можно получить число 8 8 – это 4 и … -Понравился вам урок? -Что нового узнали на уроке? — Оцените свою деятельность на уроке с помощью «Светофора», положите свою карточку в соответствующий кармашек (зелёный – все понятно, желтый – есть затруднения, красный – много непонятного) -Спасибо за урок! | Составляют числовой ряд правильно, называют четные и нечетные числа, соседей чисел, продолжают узор -Осьминог! -Рассматривают изображение осьминога, делают предположения, что у осьминога 8 ног, значит будем говорить о числе 8. -Состав числа 8. -Как можно получить число 8, составлять и решать примеры с числом 8. 1+7=8 (1 с газетой, 7 без газеты) 2+6=8 (2 взрослых, 6 детей) 3+5=8 (3 на скамейке, 5 играют) 4+4=8 (4 красных, 4 синих) Анализируя рисунки, дети дополняют, записывают равенства: 6+2=8 4+4=8 3+5=8 Первые 2 фигуры закрашивают с учителем, далее пробуют самостоятельно, дополняют примеры. Работают самостоятельно 8-1= 8-5= 1+7=8 8-7= 8-4= 2+6=8 2+6=8 Раскладывают спички по коробочкам и записывают равенства, работают в парах. 1+1+6=8 1+2+5=8 1+3+4=8 ………… Это прямая, у которой есть начало, но нет конца. Русалка, Морской царь и краб. Краб может находиться на отметке 4 и 8. От краба до Русалки – 4 или 8. Показывают с помощью веера состав числа 8 Состав числа 8, как можно получить примеры на вычитание. Оценивают урок с помощью «Светофора» |
Сообщение темы урока
Как составлено число? Запишите равенства.
.. 
Выясняют, что из примеров на сложение можно получить 2 примера на вычитание.Что такое составные числа? Объяснение для родителей и учителей
Составные числа обратны простым числам. Здесь мы объясняем, что именно означает этот раздел теории чисел, рассказываем, как его используют и изучают в начальной и средней школе, и приводим несколько примеров вопросов, связанных с составными числами.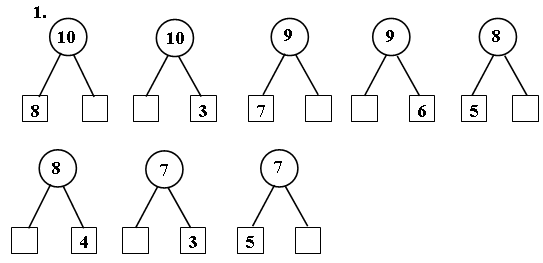
Учащиеся официально знакомятся с простыми и составными числами в 4-м классе и должны работать в диапазоне от 1 до 100.
Рабочие листы по простым числам
Загрузите этот бесплатный рабочий лист по простым числам, чтобы помочь учащимся 4-го и 5-го классов разобраться во всем, что связано с простыми числами. Включает вопросы на умножение и деление.
Что такое составное число?
В то время как простое число может иметь только 2 делителя: 1 и само число, и 3; составное число, с другой стороны, может быть любым целым числом, которое имеет более чем 2 делителя.
3 будет простым числом, потому что его делителями являются только 1 и 3. Составное число может быть четным или нечетным числом.
Помните, что составным числом может быть любое заданное целое положительное (или натуральное число), делители которого являются меньшими целыми положительными числами, при условии, что число имеет как минимум 3 делителя.
Обратите внимание, что сильно составное число имеет большое количество множителей, и объяснение этой концепции учащимся может помочь им вспомнить, что составное число имеет несколько множителей по сравнению с простым числом, которое имеет только два множителя.
Подробнее: Что такое факторы?
Примеры составных чисел включают:
- 4, так как оно имеет три делителя: 1,2 и 4.
- Между 10 есть 5 составных чисел: 4, 6, 8, 9, 10
1 не является ни простым, ни составным числом.
Составные числа в начальной школе
Термин «составные числа» формально не вводится в Единых базовых государственных стандартах до 4-го класса.
Согласно CCSS, детей 4-го класса следует учить:
«определить, является ли заданное целое число в диапазоне от 1 до 100 простым или составным».
Учащимся не будет предложено идентифицировать числа как составные вне контекста обсуждения простых чисел.
В школах, следующих стандартам штата Техас, составные числа не вводятся до 5-го класса. Ожидается, что дети 5-го класса: «Определят простые и составные числа».
Составные числа от 1 до 100
Составные числа от 1 до 100…
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Студенты не должны заучивать этот список наизусть. Использование тестов делимости для нахождения множителей числа очень полезно при определении того, является ли число простым или составным.
Учащиеся должны уметь находить простые числа до 100 и знать простые числа до 19. Тесты на простоту, такие как решето Эратосфена или просто пробное деление, могут быть методами, которые учащиеся используют, чтобы выяснить, какие числа являются простыми до число n, так как учащиеся будут работать в диапазоне небольших чисел.
Поэтому проще найти простые числа и знать, что числа, которые не являются простыми, называются составными числами.
Знакомство учащихся 4-х классов с концепцией составных чисел в рамках онлайн-интервенции Third Space Learning.Как это связано с другими областями математики?
Помимо идентификации чисел как простых или составных, маловероятно, что учащимся потребуется знать, что числа являются составными. Однако применение составных чисел используется в математике для описания формы, измерения, количественного определения количества объектов и выполнения арифметических действий.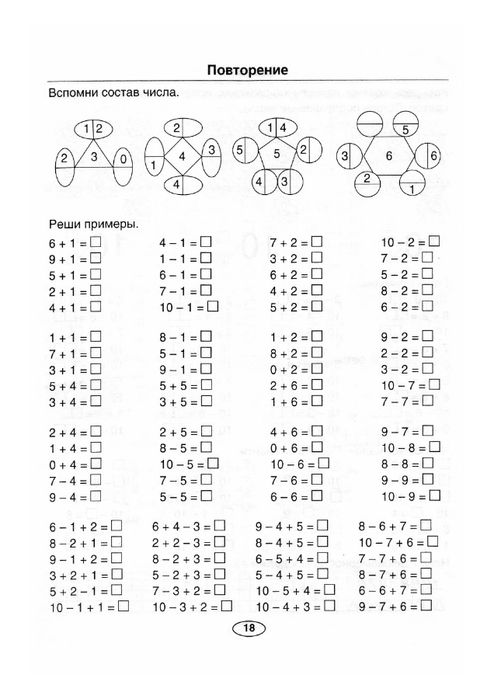
Как это связано с реальной жизнью?
Если вы не работаете в сфере кибербезопасности (где важны простые числа) или не работаете учителем, вы вряд ли столкнетесь с термином «составные числа». Однако применение составных чисел, то есть любого целого числа, не являющегося простым, используется в математике (см. выше).
Пример работы составных чисел
В. Поместите эти числа в таблицу ниже.
2,3,4,5,6,7,8,9,10
| Prime | Composite |
|---|---|
Студенты должны запомнить до первых номеров до первых номеров до первичных номеров до первых номеров до первых номеров до первых номеров до первых номеров и номеры до первых номеров, в том числе и до первых номеров, в том числе и до отметки, в том числе и в целях, в том числе и в целях, в том числе и в целях, в том числе и в том числе и в целом, в том числе и в целом, в том числе и в целом, в том числе и в целях, в том числе и в целом.
19. Они могли бы использовать это, чтобы записать простые числа в правильную часть, а затем сделать вывод, что другие числа являются составными.
| Prime | Composite |
|---|---|
| 2, 3, 5, 7 | 4, 6, 9, 10 |
для студентов, которые не знают первичных номеров до 19, они могут найти 1
. факторы каждого числа, используя их факты умножения.
2 = 2 x 1 (2 фактора)
3 = 3 x 1 (2 фактора)
4 = 4 x 1 = 2 x 2 (3 фактора)
Составные числа Примеры вопросов это определение составного числа?
(Ответ: число с более чем двумя делителями)
2. Какие из следующих чисел являются составными? 51, 97, 69, 57, 53, 90
(Ответ: 90, 69, 57, 51)
3. Энди составляет число 17 из простого и составного чисел, используя только сложение.
Какие могут быть числа?
(Ответы: 2+15, 3+14, 5+12, 7+10, 11+6, 13+4)
4. Чему равно произведение первых 3-х составных чисел?
(ответ: 192)
5. Роберт выбирает составное число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 300. Напишите все возможные составные числа, которые мог выбрать Роберт.
(Ответы: 25, 26, 27, 28, 30, 32, 33, 34)
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим математическим словарем для детей и родителей или попробуйте эти:
- Что такое математические способности?
- Видео: Как преподавать простые и составные числа
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи было первоначально написано ведущим учителем начальной школы Нилом Алмондом, а затем было отредактировано и адаптировано для школ США учителем математики начальной школы Кристи Кулешей.
Простые и составные числа. 4, 2022
Крайне важно понимать разницу между простым числом и числом 9.0003 составные числа по математике. В то время как составных числа — это числа с более чем двумя делителями. Они просто противоположны простым числам. Простые числа — это те, которые имеют только два делителя, то есть 1 и само число.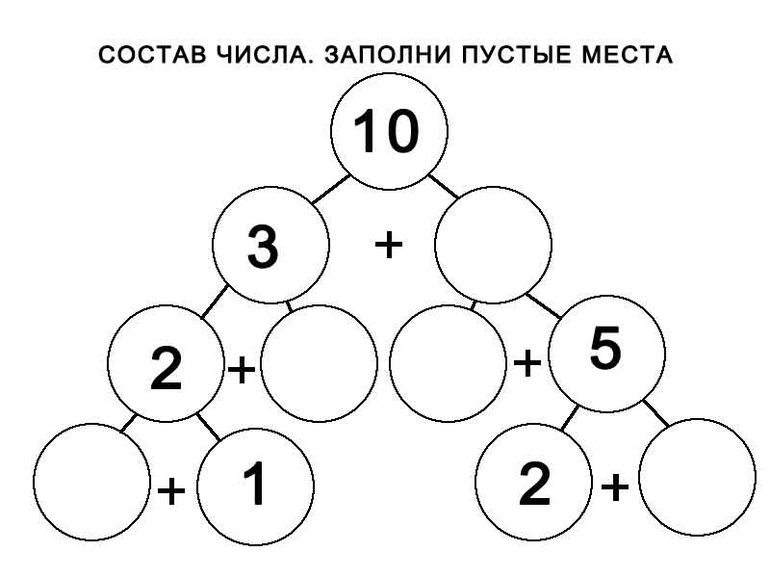
Простое число всегда натуральное число. Все натуральные числа, не являющиеся простыми, попадают в категорию составных чисел . Итак, составных числа делятся более чем на два числа. В этой статье мы узнаем следующее:
- Что такое простые и составные числа?
- Разница между простыми и составными числами
- Свойства простых и составных чисел
- Как определить простые и составные числа
- Факты о простых и составных числах
- Список составных номеров
- Таблица простых и составных чисел
Что такое простые числа?
Простое число — это положительное целое число. У него ровно два делителя: 1 и само число. Итак, если n — простое число, его делители будут равны 1 и самому n. Мы также можем определить простое число как число, которое является целым положительным числом и не является произведением любых двух других положительных целых чисел, кроме самого числа и 1. 9(82 589 933) — 1 — самое большое простое число за последнее время.
Математики все еще находят больше.
Простые числа, разность которых равна двум, являются простыми числами-близнецами. Например, 3 и 5, 5 и 7, 11 и 13 — это наборы простых чисел-близнецов. Другими словами, это два последовательных простых числа, между которыми находится только одно число.
Взаимно простые числа — это два числа, у которых есть только 1 в качестве общего делителя. Например, 2 и 3, 4 и 5, 3 и 7, 4 и 9.являются взаимно простыми числами.
Свойства простых чисел
Ниже приведены некоторые свойства простых чисел:
- Каждое простое число больше 1
- Каждое простое число само по себе является множителем
- Каждое число больше 1 можно разделить хотя бы на одно простое число.
- Каждое положительное целое число, четное и превышающее 2, может быть представлено в виде суммы двух простых чисел.
- 2 — единственное четное простое число.
- Все простые числа нечетные, кроме 2.
- Два простых числа взаимно просты друг с другом.
- Каждое составное число можно разложить на простые множители.
Список простых чисел
Вот список простых чисел от 1 до 100. Учащиеся могут понять концепцию простых чисел из этого списка и составить список, превышающий 100, для практики.
| Список простых чисел |
| 2, 3, 5, 7, 1, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
Что такое составные числа?
В отличие от простого числа, составное число — это число, имеющее более двух делителей.
Мы можем определить составных числа как числа, которые могут быть получены путем умножения двух наименьших натуральных чисел и содержат по крайней мере еще один делитель в дополнение к числу «1» и самому себе.
Все четные числа больше 2 входят в число многих примеров составных чисел.
Итак, все ли четные числа составные?
Нет, 2 — четное простое число. На самом деле, это единственное четное число, которое является простым. Следовательно, мы не можем сказать, что все четные числа — это составных числа .
Типы составных чисел
Составные числа бывают двух типов:
- Нечетные составные числа
- Четные составные числа
Все нечетные числа больше 1, не являющиеся простыми, являются нечетными составными числами.
Примерами нечетных составных чисел являются 9, 15, 21 и другие.
Четные составные числа Четные составные числа включают все четные целые числа, не являющиеся простыми числами.
Примерами четных составных чисел являются 4, 6, 8, 10 и другие.
Свойства составных чисел
Составные числа обладают следующими свойствами:
- Каждое составное число имеет более двух делителей
- Множители делят составные числа без остатка
- Составные числа тоже являются своими факторами.
- 4 — наименьшее составное число .
- Каждое составное число имеет как минимум два простых числа в качестве сомножителей.
- Составное число делится и на другие составные числа.
Список составных чисел
Вот список всех составных чисел от 1 до 100 . Учащиеся могут понять концепцию составных чисел из этого списка и создать список, превышающий 100, для практики.
| Список составных номеров |
| 4. 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 27, 22, 8, 25, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100 |
Как найти составные числа?
Вы должны найти делители числа, чтобы определить, является ли оно составным. Если множителей больше двух, то число составное.
Мы можем выполнить тест на делимость, чтобы определить, является ли число простым или составным.
В тесте на делимость мы делим число на общие множители, такие как 2, 3, 5, 7, 11 и 13. Если эти множители не могут полностью разделить число, то это число является простым числом. Например, 22 делится на 2, что означает, что оно имеет делитель 2, отличный от 1 и 22. Следовательно, 22 — составное число.
Как найти простые числа?
Существует два метода, помогающих определить, являются ли данные числа простыми или составными.
Метод 1:
Любое простое число, кроме 2 и 3, можно записать в виде 6n + 1 или 6n – 1, где n — натуральное число.
Например:
6(1) – 1 = 5
6(1) + 1 = 7
Метод 2:
Для определения числа больше 40 как простого числа мы можем использовать по следующей формуле:
n2 + n + 41, где n= 0, 1, 2, ….и выше.
Например:
(0)2 + 0 + 41 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
Разница между простыми и составными числами
Существует множество различий между простыми и составными числами.
В следующих таблицах перечислены некоторые ключевые различия между ними.
| Простые числа | Составные числа |
| У них есть 2 множителя. Единица и само число. | Они имеют более двух факторов. |
| Его можно записать в виде произведения двух чисел. | Они могут быть записаны как произведение двух или более чисел |
| Пример: Делители 7 равны 1 и 7. | Пример: Делители 6 равны 1, 2, 3 и 6 |
Таблица простых и составных чисел
Ранее математики использовали числовые таблицы для записи всех простых чисел или простых факторизаций. Решето Эратосфена представляло собой список простых чисел. Этот метод обеспечивает карту-карту Эратосфена.
На следующей диаграмме простые числа до 100 показаны в цветных прямоугольниках. Все числа, кроме цветных прямоугольников, являются составными числами.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 20 9099999999999999999999999999999999999999999999999999989999999398989RAN 9. | 999999999999999999999999999999999999999999999999999999999999999999999999989RAP010923 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | ||||||||
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | ||||||||
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | ||||||||
| 61 | 62 | 63 | 64 | 65 | . 0003 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | |||
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | ||||||||
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Похожие темы
Как найти площадь квадрата?
Площадь квадрата можно определить по тому, сколько пространства он занимает внутри себя. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как […]
Подробнее >>
Числовые последовательности: определение и типы
Числовые последовательности — важный математический инструмент для оценки чьего-либо IQ.
Большинство тестов на управленческие способности часто включают вопросы числового ряда. Вы когда-нибудь замечали закономерность в числах, отведенных домам в ряду, в номерах страниц в книге или в прибавке к зарплате, которую работник получает каждый год? Если да, вы […]
Подробнее >>
Что означает координатная сетка? — Полное руководство
Плоскость – это плоская поверхность. Так же, как пол или стена, это гладкая и плоская поверхность. Однако сетка — это нечто другое. Задумывались ли вы, как городские мегаполисы расположены в соответствии с последовательной и простой в использовании сеткой? Это окончательный пример координатной плоскости. Города с хорошо спланированной планировкой улиц […]
Подробнее >>
Вычитание с перегруппировкой
Никто не задавался вопросом, можно ли так легко использовать математику, группируя числа для облегчения вычислений. Методология становится проще, когда числа сгруппированы кратными 10 или 100.