Негосударственное общеобразовательное учреждение Средняя общеобразовательная школа

Теоретические вопросы по физике 7 класс: Тесты по физике для 7 класса онлайн

alexxlab

Вопросы к устному зачёту по физике за 7 класс | Методическая разработка по физике (7 класс) на тему:

Опубликовано 06.12.2017 — 21:30 — Муравьёва Анастасия Александровна

В документе представлены вопросы к устному зачёту по физике за курс 7 класса. Вопросы продублированы, расположены в два столбика для удобной печати.

Скачать:


Предварительный просмотр:

ЧОУ «ГАРМОНИЯ»

Теоретические вопросы

для устного зачёта по физике

 за 7 класс

Составитель:

Муравьёва А.А.,

учитель физики

Иваново, 2017 г.

  1. Как обозначается масса?
  2. В чем измеряют массу? В СИ
  3. Как обозначается объем?
  4. В чем измеряют объем? В СИ
  5. Как обозначается плотность?
  6. В чем измеряют плотность? В СИ
  7. Как обозначается сила?
  8. В чем измеряют силу? В СИ
  9. Как обозначается сила тяжести?
  10. В чем измеряют силу тяжести? В СИ
  11. Как обозначается сила упругости?
  12. В чем измеряют силу упругости? В СИ
  13. Как обозначается сила трения?
  14. В чем измеряют силу трения? В СИ
  15. Как обозначается давление?
  16. В чем измеряют давление? В СИ
  17. Как обозначается удлинение пружины?
  18. В чем измеряют удлинение пружины? В СИ
  19. Как обозначается высота столба жидкости (глубина)?
  20. В чем измеряется жидкости (глубина)? В СИ
  21. Как обозначается площадь?
  22. В чем измеряется площадь? В СИ
  23. Как обозначается атмосферное давление?
  24. В чем измеряют атмосферное давление? В СИ
  25. Как обозначается сила Архимеда?
  26. В чем измеряется сила Архимеда? В СИ
  27. Как обозначается вес тела?
  28. В чем измеряется вес тела? В СИ
  29. Как обозначается работа?
  30. В чем измеряется работа? В СИ
  31. Как обозначается мощность?
  32. В чем измеряется мощность? В СИ
  33. Как обозначается путь, расстояние?
  34. В чем измеряется путь, расстояние? В СИ
  35. Как обозначается скорость?
  36. В чем измеряется скорость? В СИ
  37. Как обозначается время?
  38. В чем измеряется время? В СИ
  39. Как обозначается плечо рычага?
  40. В чем измеряется плечо рычага? В СИ
  41. Как обозначается момент силы?
  42. В чем измеряется момент силы? В СИ
  43. Как обозначается работа?
  44. В чём измеряется работа? В СИ
  45. Как обозначается мощность?
  46. В чём измеряется мощность?
  47. Как обозначается энергия?
  48. В чём измеряется энергия? В СИ
  49. Как обозначается кинетическая энергия?
  50. В чём измеряется кинетическая энергия? В СИ
  51. Как обозначается потенциальная энергия?
  52. В чём измеряется потенциальная энергия? В СИ
  53. Формула для силы тяжести.
  54. Формула для силы упругости
  55. Формула для давления твердого тела
  56. Формула для давления жидкости
  57. Формула для силы Архимеда
  58. Формула для работы
  59. Формула для мощности
  60. Формула для момента силы
  61. Формула для работы
  62. Формула для мощности
  63. Формула для кинетической энергии
  64. Формула для потенциальной энергии
  65. Формула-закон сохранения энергии
  1. Как обозначается масса?
  2. В чем измеряют массу? В СИ
  3. Как обозначается объем?
  4. В чем измеряют объем? В СИ
  5. Как обозначается плотность?
  6. В чем измеряют плотность? В СИ
  7. Как обозначается сила?
  8. В чем измеряют силу? В СИ
  9. Как обозначается сила тяжести?
  10. В чем измеряют силу тяжести? В СИ
  11. Как обозначается сила упругости?
  12. В чем измеряют силу упругости? В СИ
  13. Как обозначается сила трения?
  14. В чем измеряют силу трения? В СИ
  15. Как обозначается давление?
  16. В чем измеряют давление? В СИ
  17. Как обозначается удлинение пружины?
  18. В чем измеряют удлинение пружины? В СИ
  19. Как обозначается высота столба жидкости (глубина)?
  20. В чем измеряется жидкости (глубина)? В СИ
  21. Как обозначается площадь?
  22. В чем измеряется площадь? В СИ
  23. Как обозначается атмосферное давление?
  24. В чем измеряют атмосферное давление? В СИ
  25. Как обозначается сила Архимеда?
  26. В чем измеряется сила Архимеда? В СИ
  27. Как обозначается вес тела?
  28. В чем измеряется вес тела? В СИ
  29. Как обозначается работа?
  30. В чем измеряется работа? В СИ
  31. Как обозначается мощность?
  32. В чем измеряется мощность? В СИ
  33. Как обозначается путь, расстояние?
  34. В чем измеряется путь, расстояние? В СИ
  35. Как обозначается скорость?
  36. В чем измеряется скорость? В СИ
  37. Как обозначается время?
  38. В чем измеряется время? В СИ
  39. Как обозначается плечо рычага?
  40. В чем измеряется плечо рычага? В СИ
  41. Как обозначается момент силы?
  42. В чем измеряется момент силы? В СИ
  43. Как обозначается работа?
  44. В чём измеряется работа? В СИ
  45. Как обозначается мощность?
  46. В чём измеряется мощность?
  47. Как обозначается энергия?
  48. В чём измеряется энергия? В СИ
  49. Как обозначается кинетическая энергия?
  50. В чём измеряется кинетическая энергия? В СИ
  51. Как обозначается потенциальная энергия?
  52. В чём измеряется потенциальная энергия? В СИ
  53. Формула для силы тяжести.
  54. Формула для силы упругости
  55. Формула для давления твердого тела
  56. Формула для давления жидкости
  57. Формула для силы Архимеда
  58. Формула для работы
  59. Формула для мощности
  60. Формула для момента силы
  61. Формула для работы
  62. Формула для мощности
  63. Формула для кинетической энергии
  64. Формула для потенциальной энергии
  65. Формула-закон сохранения энергии

По теме: методические разработки, презентации и конспекты

Вопросы для устного зачета по геометрии 8 класс

Устный зачет, тема «Подобие треугольников», углубленный курс геометрии, 8 класс.Зачет проводится по группам по 4-5 учащихся в форме блиц-опроса на знание формулировок теорем, определений.Время для отв…

Зачёт по физике.7 класс.

Задания к зачётам по физике.(Базовый учебник:  Физика 10 класс, авторы: Г.Я. Мякишев. Б.Б. Буховцев, Н.Н. Сотский, «Просвещение», Москва )….

Вопросы к устному зачёту по теме ЛИЧНОСТЬ

Вопросы помогут Вам успешнее подготовиться к устному собеседованию. Вопросы составлены с опорой на параграфы учебника Боголюбова Обществознание. См.§§16, 28,29,30….

вопросы к зачёту по физике 11 класс

вопросы к зачёту по физике 11 класс…

зачёт по физике 8 класс

В данной работе представлены вопросы к устному зачёту по физике в 8 классе. Зачёт проводится в конце учебного года….

зачёт по физике 11 класс «Электромагнитные волны «

зачёт в тестовой форме…

Вопросы к устному зачёту по билетам. История, профиль, 11 класс.

Билеты для ответов по темам истории России с 1861 по 1941 г….


Поделиться:

 

Физика 7 класс. Тесты, тренажеры, контрольные работы

ВПР 2019. Физика 7 класс. Тренировочный тест. 

 

Тесты и тренажеры по физике

 

Контрольные работы по физике с ответами
УМК
Перышкин — Громцева.  Контрольные работы по физике.
УМК
Перышкин — Марон. СиКР: Контрольные работы
УМК
Перышкин — Марон. СиКР: Самостоятельные работы
УМК
Перышкин — Марон. Дидактические материалы: Контрольные работы
УМК
Перышкин — Марон. Дидактические материалы: Самостоятельные работы
УМК
Перышкин — Кирик. Контрольная работа «Архимедова сила».
К любому УМК —
Годова. Физика 7. Контрольные работы в новом формате (годовая)

 

Онлайн-учебники и конспекты по физике
Онлайн-конспекты по физике 7-9 классы
Онлайн-учебник
Физика. 7 класс Перышкин

 

Физика 7 класс. Основные темы

Что такое физика. Физические величины. Измерение физических величин. Роль и место механики в физике.

Глава 1. Кинематика

Положение тела в пространстве. Механическое движение. Относительность механического движения. Способы описания прямолинейного движения. Прямолинейное равномерное движение. Скорость прямолинейного равномерного движения. Решение задач кинематики. Задача «встреча». Графический способ решения. Решение задач кинематики. Задачи «встреча», «погоня», «обгон». Решение задач кинематики в общем виде. Анализ полученного результата. Движение тел относительно друг друга. Задачи «встреча» и «погоня». Перемещение. Путь. Путь при прямолинейном равномерном движении. Прямолинейное неравномерное движение. Средняя скорость. Мгновенная скорость. Ускорение. Прямолинейное равноускоренное движение. Путь при прямолинейном равноускоренном движении в одном направлении. Решение задач. Задачи «разгон» и «торможение». Свободное падение тел

Глава 2. Динамика

Действие одного тела на другое. Закон инерции. Инерциальные системы отсчёта. Первый закон Ньютона. Сила. Сложение сил. Измерение силы. Масса тела. Плотность вещества. Второй закон Ньютона. Взаимодействие тел. Третий закон Ньютона

Глава 3. Силы в механике

Сила тяжести. Сила упругости. Зависимость силы упругости от деформации. Закон Гука. Сила реакции опоры. Вес. Динамометр. Силы трения

Глава 4. Механическая работа. Энергия.  Закон сохранения механической энергии

Механическая работа. Решение задач на вычисление работы сил. Кинетическая энергия. Система тел. Потенциальная энергия. Механическая энергия системы тел. Закон сохранения механической энергии. Мощность

Глава 5. Статика

Равновесие тела. Момент силы. Применение условий равновесия твёрдого тела. Решение задач на статику. Простые механизмы.

Глава 6. Давление жидкостей и газов

Сила давления и давление. Атмосферное давление. Закон Паскаля. Гидростатическое давление. Сообщающиеся сосуды. Измерение давления. Закон Архимеда.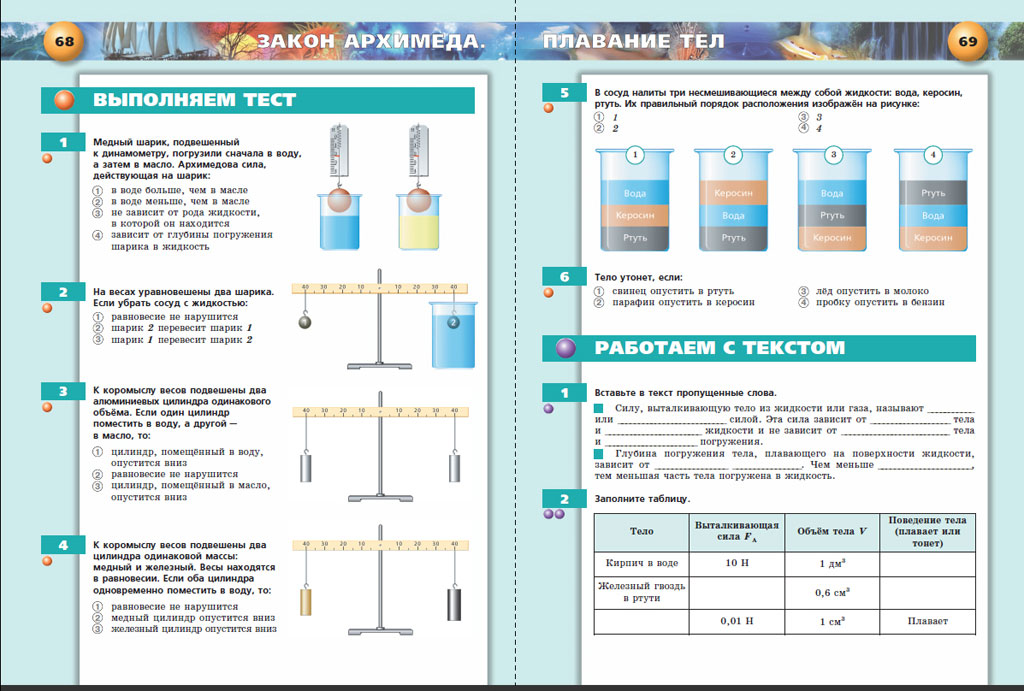 Плавание тел. Воздухоплавание.

 Рекомендуемые материалы для очного контроля знаний


по предмету «Физика» для 7 класса:

Контрольно-измерительные материалы. Физика. 7 класс / Н.И.Зорин — М.: ВАКО, 2017 (КИМ)
Физикa в 7 классе. Контрольные измерительные материалы / Бобошина — М.: Издательство «Экзамен», 2014
Контрольные и самостоятельные работы по физике. 7 кл. к учебнику Перышкина А.В. — Громцева О.И. (2016, 112с.)
Тесты по физике. 7 класс к учебнику Перышкина А.В. «Физика. 7 кл.» Чеботарева А.В. (2017, 176с.)
Физика в 7 классе. Тесты к учебнику Перышкина А.В. — Ханнанов Н.К., Ханнанова Т.А. (2014, 112с.)
Физикa. 7 класс. Диагностические работы к уч. А.В. Перышкина. — Шахматова В.В., Шефер О.Р. (2015, 126с.)
Физика. 7 класс. Проверочные и контрольные работы. Пурышева Н.С., Лебедева О.В., Важеевская Н.Е. (2014, 96с.)

Физикa. 7 класс. Разноуровневые самостоятельные и контрольные работы. Кирик Л.А. (2014, 192с.)

Перейти на Главную страницу сайта.

Вопросы критического мышления по физике — AP Central

Введение

Акцент на концептуальном понимании, методах решения задач и лабораторных работах в курсах AP Physics требует использования различных аудиовизуальных средств и демонстраций для ясного и глубокого понимания обсуждаемых тем. Постановка сложных вопросов по физике будет стимулировать навыки критического мышления у учащихся. Следующие действия помогут учащимся лучше понять концепции курсов и положительно повлияют на их результаты на экзамене. Эти вопросы сосредоточены на следующих темах критического мышления:

Часть 1

Единицы и размеры: 1-3
Расстояние и перемещение: 4-6
Кинематика и движение снаряда: 7-13
Круговое движение: 14

Вес и невесомость: 15-18
Угловой момент: 19
Электричество и магнетизм: 20- 21

Часть 2

Теплофизика: 22-24
Гидромеханика: 25-32
Волны и оптика: 33-35
Современная физика: 36

Вопросы критического мышления по физике: Часть 1

  1. 1 доллар США = 100 центов
    = 10 центов x 10 центов
    = $(1/10) x $(1/10)
    = $(1/100)
    = 1 цент

    Ответ: Неверное использование единиц измерения. На втором этапе эффективная единица ¢ 2 не совпадает с $ в левой части. Опять же, единица 2 долларов на шаге 3 изменяется на доллары на четвертом шаге.
     

  2. Эйфелева башня имеет массу 10 000 000 кг. Модель башни в масштабе 100:1, изготовленная из того же материала, будет иметь массу

    1. 100 000 кг
    2. 10 000 кг
    3. 1000 кг
    4. 100 кг
    5. 10 кг
    6. 1 кг

    Ответ: (E) 10 кг

    Некоторые учащиеся могут перейти к ответу 100 000 кг, думая, что модель будет весить 1/100 реальной башни. Однако, если высота модели составляет 1/100 высоты башни, все ее размеры равны 1/100. Следовательно, модель равна (1/100) x (1/100) x (1/100) = 1 миллионная часть объема фактической башни (независимо от того, какой формы башня). Так что если модель сделана из того же материала, что и башня, то ее масса будет равна 1 миллионной массы башни, т. е. 10 кг.
     

  3. Трое мужчин — A, B и C — пересеклись в лесу холодной ночью. Они решили разжечь костер, чтобы отдохнуть, и отправились собирать дрова. A вернулся с 5 бревнами, B принес 3 бревна, а C вернулся ни с чем. С попросил дать ему отдохнуть у костра и пообещал заплатить им немного денег утром. Утром С заплатил им 8 долларов. Как А и В должны справедливо разделить деньги?

    1. А 7 долларов; В $1
    2. 6 долларов США; Б $2
    3. 5 долларов США; Б $3
    4. 4 доллара США; В $4
    5. Ни один из этих

    Ответ: (A) A $7; Б $1

    Все трое в равной степени получают пользу от огня из 8 поленьев. Каждый мужчина использовал 8/3 бревна за ночь. Следовательно,
    А дал 5 — 8/3 = 7/3 бревна древесины.
    B внес 3 — 8/3 = 1/3 бревна дерева.
    Следовательно, они должны разделить 8 долларов в пропорции 7/3:1/3 или 7:1.
     

  4. Насекомое карабкается по вертикальной стене высотой 30 футов. Начиная снизу, днем ​​он поднимается на 3 фута, а ночью соскальзывает на 2 фута. Через сколько дней он достигнет вершины стены?

    1. 31 день
    2. 30 дней
    3. 29 дней
    4. 28 дней
    5. 27 дней
    6. Никогда

    Ответ: (D) 28 дней

    Некоторые учащиеся могут ответить 30 дней, утверждая, что насекомое вырастает на 1 фут в день.

    Но за 27 дней он поднимется на 27 футов, а на 28-й день преодолеет оставшиеся 3 фута, чтобы достичь вершины.
     

  5. Человек где-то на земле проходит 10 миль. на юг, затем 10 миль. на восток, затем 10 миль. к северу. Он вернулся в исходную точку. В каком месте на земле он?

    Ответ: На Северном полюсе есть одно решение, а на Южном полюсе — бесконечное количество решений, как показано на диаграммах ниже.

  6. Путешественник начал подниматься в гору в 6:00 утра и либо продолжал подниматься, либо отдыхал в каком-то месте (местах). Он достиг вершины в 18:00. Там он отдыхал следующие 12 часов. На следующий день в 6 часов утра он начал движение по тому же пути. Он либо двигался вниз, либо отдыхал в каком-то месте. Что касается поездок вверх и вниз, сколько раз он был в одном и том же месте в одно и то же время?

    1. Никогда
    2. Хотя бы один раз
    3. Один и только один раз
    4. Не более одного раза
    5. Только дважды
    6. Ни один из этих

    Ответ: (C) Один и только один раз

    Метод 1. Нарисуйте график зависимости x от t для туриста, где t варьируется от 6:00 до 18:00. на два дня. Графики для двух поездок будут пересекаться только для одного значения x.

    Метод 2. Представьте, что когда турист начинает подъем, есть «виртуальный турист», который начинает спуск в 6:00 утра. Легко видеть, что два «туриста» встретятся один и только один раз.
     

  7. Мистер Физ возвращается домой со скоростью 2 мили в час со своей собакой Икс. Он выпускает Икса, когда они все еще в 3 милях от его дома. Икс радостно начинает бегать туда-сюда между домом и своим хозяином с постоянной скоростью 3 мили в час. Икс не тратит время зря, поворачиваясь. К тому времени, как мистер Физ доберется до дома, сколько миль пробежит Икс?

    1. 3,5 мили
    2. 4,0 мили
    3. 4,5 мили
    4. 3,333… миль
    5. 3,555… миль
    6. Ни один из этих

    Ответ: (C) 4,5 мили

    Некоторые учащиеся могут попытаться составить ряд суммирования расстояний, пройденных собакой за время поездок между домом и хозяином. Это становится очень сложным.

    Простое решение: мистеру Физу нужно полтора часа, чтобы добраться до дома. Следовательно, собака бегает уже полтора часа. Со скоростью 3 мили в час собака прошла расстояние (3 мили в час) x (1½ часа) = 4,5 мили.
     

  8. Человек едет из города А в город Б со скоростью 40 миль в час и возвращается со скоростью 60 миль в час. Какова его средняя скорость в пути?

    1. 100 миль/ч
    2. 50 миль в час
    3. 48 миль/ч
    4. 10 миль в час
    5. Ни один из этих

    Ответ: (C) 48 миль в час

    Ответ не зависит от расстояния между городами A и B. Предположим, что расстояние равно x, а расстояние туда и обратно равно 2x. Время пути из А в В равно х/40 ч, а время обратного пути х/60 ч. Для скоростей 40 миль в час и 60 миль в час время в оба конца составляет 2x/40 ч и 2x/60 ч. Средняя скорость определяется как V avg = общее расстояние ÷ общее время.

    Это становится упражнением в арифметике дробей. Ответ оказывается равным 48 милям в час, независимо от x. Студенты, скорее всего, перескочат к ответу 50 миль в час, так как это среднее значение заданных скоростей. Однако это не то, как определяется средняя скорость!
     

  9. Два поезда движутся навстречу друг другу со скоростью 17 миль в час и 43 мили в час. На каком расстоянии они будут друг от друга за 1 минуту?

    1. 60 миль
    2. 30 миль
    3. 6 миль
    4. 3 мили
    5. 2 мили
    6. 1 миля

    Ответ: (F) 1 миля

    Нет необходимости выполнять утомительные вычисления, если мы поймем, что каждый поезд приближается к другому с относительной скоростью (17 миль в час + 43 мили в час) = 60 миль в час = 1 миля/мин. Следовательно, за 1 минуту до столкновения они находятся на расстоянии 1 км друг от друга.

  10. Два шарика катятся по двум горизонтальным дорожкам. На одной дорожке есть провал, а на другой — бугор такой же формы. Какой мрамор победит?

    Ответ: На прямых участках пути два шарика имеют одинаковую скорость.

    Однако в каждой точке падения шарик имеет большую скорость, чем другой шарик в соответствующей точке горба. Таким образом побеждает шарик на дорожке с провалом. Этот аргумент предполагает, что шарики всегда остаются в контакте с дорожками.

  11. Три снаряда выпущены из одной точки над ровной поверхностью со скоростями V A , V B и V C . Все они достигают одинаковой максимальной высоты. Что из следующего верно относительно времени их полета?

    1. т А = т В = т С
    2. т А > т В > т С
    3. т А < т В < т С
    4. Ни один из этих

    Ответ: (A) t A = t B = t C

    : Три снаряда имеют одинаковую максимальную высоту, следовательно, они имеют равные начальные вертикальные компоненты для своих скоростей. Таким образом, все они занимают одинаковое время, чтобы достичь максимальной высоты и вернуться на землю.

    (Учащиеся могут подумать, что, поскольку снаряды проходят разное расстояние по траектории, у них разное время в пути.)
     

  12. Три снаряда запускаются из одной точки над ровной поверхностью со скоростями V A , V B и V С . Все они достигают одинаковой максимальной высоты. Что из следующего верно относительно их начальной скорости?

    1. В А = В В = В С
    2. В А > В В > В С
    3. В А < В В < В С
    4. Ни один из этих

    Ответ: (C) V A < V B < V C

    Три снаряда имеют одинаковую начальную скорость и одинаковое время полета. Однако для их горизонтальных диапазонов X А < Х В < Х С . Горизонтальный диапазон обусловлен горизонтальными составляющими их скоростей в одно и то же время. Отсюда V Ax < V Bx < V Cx . Отсюда следует, что V A < V B < V C .
     

  13. Мяч несколько раз брошен с одной и той же высоты с одной и той же скоростью V o , но в разных направлениях A, B и C, как показано ниже. Он достигает земли со скоростью V A , V B и V C соответственно. Что из следующего верно относительно этих скоростей?

    1. В А = В В = В С
    2. В А > В В > В С
    3. В А < В В < В С
    4. Ни один из этих

    Ответ: (А) В А = В В = В С

    В каждом случае мяч стартует с одинаковой скоростью и, следовательно, с одинаковой кинетической энергией. Когда мяч ударяется о землю, он теряет такое же количество гравитационной потенциальной энергии и, следовательно, получает такое же количество кинетической энергии. Таким образом, в каждом случае мяч падает на землю с одинаковой скоростью.
    Здесь учащиеся могут подумать, что направление начальной скорости может влиять на скорость удара о землю.
     

  14. Барабан вращается с постоянной скоростью с вертикальной осью. Капля воды в точке Р на его поверхности отрывается и улетает. Глядя сверху, каков наиболее вероятный путь падения?

    Ответ: Капля воды P первоначально движется равномерно по окружности. Следовательно, в любой момент его скорость тангенциальна поверхности барабана. Когда он отделяется от барабана, больше нет центростремительной силы, заставляющей его двигаться по круговой траектории, поэтому он перемещается по касательной от поверхности.

    На трехмерном изображении капля будет падать на землю по параболе.
     

  15. Вес закрытой банки равен W, пока мухи внутри нее летают. Каков будет вес банки, если мухи поселятся внутри банки?

    1. Равен W
    2. Менее Вт
    3. Менее Вт

    Ответ: (A) Равно W

    Когда мухи летают, они давят на воздух, который, в свою очередь, давит на банку. На самом деле банка поддерживает мух, даже когда они летают. Если бы банку поместили на чувствительные весы, показания колебались бы около W и усреднялись бы на W в течение длительного интервала времени.
     

  16. Взвешивают закрытый сосуд с газом. Вносят ли молекулы газа вклад в измеряемый вес?

    1. Да, полностью
    2. Да, но частично
    3. №

    Ответ: (A) Да, полностью

    Может показаться, что это похоже на вопрос 15. Однако в данном случае мы рассматриваем вопрос о том, влияет ли вес самого газа на вес всей системы. Один из подходов к этой проблеме состоит в рассмотрении вертикальных скоростей молекул. Когда молекула движется вниз, ее скорость увеличивается из-за ускорения под действием силы тяжести. Когда молекула сталкивается с дном сосуда, она передает силу, превышающую ее вес; избыточная сила как раз компенсирует время, в течение которого молекула не контактировала с банкой.

    Опять же, в микроскопическом масштабе, если банку поставить на чувствительные весы, показания весов будут варьироваться в районе W, но в среднем будут составлять W в течение достаточно длительного интервала времени.
     

  17. Как космонавты взвешиваются в состоянии невесомости?

    Ответ: Вес космонавтов на близкой орбите вокруг Земли составляет около 90 процентов от их веса на поверхности Земли. Однако они чувствуют себя невесомыми, потому что фактически находятся в свободном падении и, следовательно, не имеют нормальной силы от поверхности, действующей на них. Нормальная сила дает людям ощущение своего веса. Если человек встает на весы, чтобы определить свой вес, весы считывают нормальную силу, которую они прикладывают для поддержки этого человека. Следовательно, весы покажут нулевой вес для космонавта, если он «стоит» на таких весах в спутнике. Однако космонавты могут найти свою массу (инерцию), используя тот факт, что период колебаний системы пружина-масса зависит от присоединенной к ней массы, а не от силы тяжести. Устройство, разработанное НАСА по этому принципу, называется устройством для измерения массы тела (BMMD).
     

  18. Человек, несущий чашку воды с плавающим льдом, входит в лифт. Если лифт ускорится вверх, лед будет

    1. Поплавок выше
    2. Раковина глубже
    3. Остаться на прежнем уровне

    Ответ: (C) Оставайтесь на том же уровне

    Система отсчета с ускорением вверх эквивалентна инерциальной системе отсчета с более высоким значением ускорения свободного падения, определяемым как g’ = g + a. Выталкивающая сила на льду обусловлена ​​давлением воды, которое пропорционально силе тяжести g’. Вес блока составляет мг’. Следовательно, и вес блока, и выталкивающая сила увеличиваются в один и тот же раз при ускорении лифта вверх (и уменьшаются в один и тот же раз при ускорении лифта вниз). Поэтому лед плавает на одном уровне, а уровень воды в чашке не меняется.
     

  19. Почему у вертолета рядом с хвостом второй винт?

    Ответ: Так как основной (горизонтальный) винт вращается в одну сторону, то остальная часть вертолета стремится вращаться в противоположную сторону по закону сохранения углового момента. Вращение основного корпуса вертолета может быть предотвращено другим винтом рядом с хвостовой частью вертолета.
     

  20. В комнате есть три переключателя A, B и C. Два из них — фиктивные выключатели, а третий — выключатель настольной лампы в другой комнате. Вы можете включать и выключать три переключателя по своему усмотрению. Затем вы входите в комнату с настольной лампой только один раз и можете сказать, какой из выключателей является правильным для лампы. Как вы можете это сделать?

    Ответ: Включите переключатель А. Оставьте на несколько минут. Выключите A и включите B. Подойдите к настольной лампе.

    Если лампа горит, это B.

    Если лампа выключена и колба теплая на ощупь, это А.

    Если лампа выключена и колба холодная на ощупь, это C.
     

  21. Мальчик несет металлический стержень PQ горизонтально на пикапе, едущем по прямой горизонтальной дороге. В стержне индуцируется ЭДС из-за магнитного поля Земли, что делает конец P положительным (+), а конец Q отрицательным (-). Концы стержня теперь соединены проволокой. В каком направлении будет течь индуцированный ток в стержне, если он есть?

    1. от P до Q
    2. Q-P
    3. Через стержень не будет протекать ток.

    Ответ: (C) Через стержень не будет течь ток.

    Стержень и проволока образуют замкнутый контур. Магнитный поток через петлю не изменяется при прямолинейном движении грузовика. Следовательно, по закону Фарадея в петле нет ни ЭДС индукции, ни индукционного тока.

Вопросы критического мышления по физике. Часть 2

  1. Две одинаковые чашки P и Q содержат одинаковое количество горячего кофе одинаковой температуры. Теперь в чашку P добавляют холодные сливки. Через несколько минут такое же количество холодных сливок при той же температуре добавляют в чашку Q. Сравните новые температуры T P и T Q кофе в чашке. две чашки.

    1. Т Р = Т Q
    2. Т П > Т В
    3. Т Р < Т Q

    Ответ: (B) T P > T Q

    Это вопрос о теплопередаче и законе охлаждения Ньютона. Тело при более высокой температуре отдает тепло окружающей среде с большей скоростью. Поскольку чашка Q находилась при более высокой температуре в течение более длительного интервала времени, она потеряла больше тепла.
     

  2. Металлический стержень АВ согнут в показанную форму.

    Если стержень нагревается равномерно, пространство между концами будет

    1. Увеличение
    2. Уменьшение
    3. Оставайся прежним

    Ответ: (A) Увеличение

    При тепловом расширении объекта любой формы каждая частица удаляется от любой другой частицы. Если точки А и В сблизятся, расширение будет противоположным.

    Прямые участки, заканчивающиеся точками A и B, расширяются и заставляют точки A и B сближаться. Однако расширение нижнего отрезка прямой раздвигает точки A и B. Длина нижнего сегмента больше, чем общая длина двух верхних сегментов. Следовательно, чистый эффект заключается в том, что точки A и B отдаляются друг от друга.

  3. Контейнер разделен на две половины перегородкой с отверстием. Две половины содержат один и тот же газ, но при разных температурах. Какая половина содержит большее количество газа?

    1. Половинка при более высокой температуре
    2. Половина при более низкой температуре
    3. Половинки содержат одинаковое количество газа.

    Ответ: (B) Половина при более низкой температуре

    Ответ можно быстро найти, используя известное уравнение PV = nRT. Отверстие в перегородке обеспечивает одинаковое давление в обеих половинах. Отсюда и количество молей.

  4. Бутылка полностью заполнена водой, как показано на схеме ниже. Какие из показанных точек имеют одинаковое давление?

    1. Р 1 и Р 2
    2. Р 2 и Р 3
    3. Р 1 и Р 3
    4. P 1 , P 2 и P 3
    5. Ни один из этих

    Ответ: (B) P 2 и P 3

    Давление жидкости в точке пропорционально глубине точки под открытой поверхностью жидкости. Это верно, даже если открытая поверхность не находится вертикально над точкой, как в случае с точкой P 3 . Можно подумать, что P 1 и P 3 имеют одинаковое давление, так как оба они находятся на 10 см ниже поверхности жидкости. Это неверно, потому что поверхность воды непосредственно над P 3 не является открытой поверхностью.
     

  5. Два одинаковых стакана держат воду на одной высоте, но в одном из них плавает деревянный брусок. Какой стакан весит больше?

    1. А
    2. Б
    3. Ни

    Ответ: (С) Ни

    Количество воды в стакане B меньше, чем в стакане A из-за воды, вытесненной плавающим блоком. Однако, применяя принцип Архимеда, вес плавающего блока равен весу вытесненной им воды.
     

  6. Два одинаковых стакана держат воду на одной высоте, но в одном из них полностью погружен деревянный брусок, прикрепленный на дне веревкой. Какой стакан весит больше?

    1. А
    2. Б

    Ответ: (А)

    В стакане B вытесненный объем воды заменен деревянным бруском меньшей плотности. Следовательно, он меньше весит.
     

  7. Два одинаковых стакана держат воду на одной высоте, но в один из них погружен железный брусок. Какой стакан весит больше?

    1. А
    2. Б
    3. Ни

    Ответ: (Б)

    В стакане В объем вытесненной воды занимает железный блок большей плотности. Следовательно, он весит больше.
     

  8. Два одинаковых стакана держат воду на одной высоте, но в одном из них на веревке подвешен железный блок. Какой стакан весит больше?

    1. А
    2. Б
    3. Ни

    Ответ: (С) Ни

    В стакане B отсутствует вода, вытесненная частично погруженным железным блоком. Выталкивающая сила, действующая на брусок, равна весу вытесненной воды. Эта сила также действует на дно стакана как реактивная сила и точно компенсирует уменьшение веса из-за недостатка воды.

  9. Два одинаковых стакана держат воду на одной высоте, но в одном из них на веревке подвешен полностью погруженный в воду железный блок. Какой стакан весит больше?

    1. А
    2. Б
    3. Ни

    Ответ: (С) Ни

    В стакане B на железный блок действует выталкивающая сила, равная весу вытесненной воды. Выталкивающая сила действует водой вверх на блок и как реакция вниз на дно стакана, таким образом компенсируя вес вытесненной воды.
     

  10. Лодка в озере бросает якорь в озеро. Уровень озера будет

    1. Остаться прежним
    2. Подъем
    3. Осень

    Ответ (С) Осень

    Находясь в лодке, якорь вытесняет воду, равную собственному весу. Поскольку плотность якоря больше плотности воды, объем вытесненной воды больше объема якоря. Когда якорь бросают в воду, якорь вытесняет объем, равный его собственному объему. Следовательно, объем воды, вытесняемой при броске якоря в озеро, меньше, чем при броске якоря в лодке, и уровень озера падает.
     

  11.  

    По озеру плывет двухтонная лодка. Выталкивающая сила на лодке должна быть
     
    1. 2 тонны
    2. Более 2 тонн
    3. Менее 2 тонн
    4. В зависимости от плотности воды в озере

    Ответ: (А) 2 тонны

    Находясь в лодке, якорь вытесняет воду, равную собственному весу. Поскольку плотность якоря больше плотности воды, объем вытесненной воды больше объема якоря. При падении якоря в воду якорь вытесняет объем, равный его собственному объему. Следовательно, объем воды, вытесняемой при броске якоря в озеро, меньше, чем когда якорь находился в лодке. Таким образом уровень озера падает.
     

  13. Когда мы смотрим на себя в плоское зеркало, мы видим перестановку влево-вправо, но не перестановку вверх-вниз. Почему?

    Ответ: В плоском зеркале имеется инверсия глубины и нет инверсии влево-вправо. Право оказывается правым, лево — левым, верх — верхом, а низ — низом. Однако для человека, смотрящего в зеркало, возникает иллюзия переворота влево-вправо, а не переворота вверх-вниз. Это связано с тем, что для того, чтобы другой человек оказался лицом к наблюдателю, другой человек всегда поворачивается вокруг вертикальной оси, вызывая реальную перестановку влево-вправо.
     

  14. Длина волны красного света в воде близка к синему, но красные знаки выхода кажутся пловцу красным, находящемуся внутри воды. Почему?

    Ответ: Когда свет входит в среду из другой среды, его длина волны и скорость меняются, а частота остается прежней. На длину волны во второй среде не влияет введение третьей среды между двумя средами. Таким образом, красный свет, попадающий в глаз непосредственно из воздуха, имеет внутри глаза ту же длину волны, что и красный свет, сначала попадающий в воду, а затем в глаз, поэтому красный свет кажется пловцу под водой красным.
     

  15. Наши глаза наиболее чувствительны к зеленовато-желтому свету, но сигналы опасности красные. Почему?

    Ответ: Красный свет может проникать через атмосферу, содержащую пыль, облака и туман, намного эффективнее, чем любой другой цвет. Свет в синей части видимого спектра в гораздо большей степени рассеивается атмосферой. Вот почему небо кажется голубым, а закатное и восходное небо красноватым.
     

  16. Почему рождение электрон-позитронных пар не может происходить в вакууме?

    Ответ: Парное образование – это создание пары электрон-позитрон фотоном гамма-излучения. В этом процессе фотон исчезает, а его энергия преобразуется в массу покоя пары электрон-позитрон и кинетическую энергию, которую они несут. Часть энергии фотона превращается в массу покоя электрон-позитронной пары. Таким образом, линейный импульс пары меньше импульса фотона; это нарушение закона сохранения импульса. Следовательно, рождение пар всегда происходит вблизи тяжелого ядра. Отдача ядра констатирует сохранение импульса.

Автор:

Хасан Фахруддин
Академия наук, математики и гуманитарных наук Индианы BSU
Манси, Индиана

Вопросы по физике

На этой странице я собрал коллекцию вопросов по физике, чтобы помочь вам лучше понять физику. Эти вопросы предназначены для того, чтобы бросить вызов физике и вдохновить ее на более глубокие размышления о физике. Эти вопросы не только сложные, но и веселые и интересные. Эта страница является хорошим ресурсом для студентов, которым нужны качественные задачи для практики при подготовке к тестам и экзаменам.

Чтобы просмотреть вопросы, нажмите на интересующую вас категорию:

Вопросы по физике для старших классов
Вопросы по физике для колледжей и университетов
дополнительных сложных вопросов по физике

Вопросы по физике для старших классов

Проблема № 1

Падают ли более тяжелые предметы медленнее, чем более легкие?

См. решение

Проблема № 2

Почему объекты плавают в жидкостях более плотных, чем они сами?

См. решение

Проблема № 3

Частица движется по окружности, и ее положение задается в полярных координатах как x = Rcosθ , и y = Rsinθ , где R — радиус окружности, а в радианах. Из этих уравнений выведите уравнение для центростремительного ускорения.

См. решение

Проблема № 4

Почему в свободном падении вы чувствуете себя невесомым, хотя гравитация притягивает вас? (не учитывайте сопротивление воздуха при ответе на этот вопрос).

См. решение

Проблема № 5

В чем разница между центростремительным ускорением и центробежной силой?

См. решение

Проблема № 6

В чем разница между энергией и мощностью?

См. решение

Проблема № 7

Два одинаковых автомобиля сталкиваются лоб в лоб. Каждая машина едет со скоростью 100 км/ч. Сила удара каждой машины такая же, как при ударе о сплошную стену в точке:

(а) 100 км/ч

(б) 200 км/ч

(в) 150 км/ч

(г) 50 км/ч

См. решение

Проблема № 8

Почему можно забить гвоздь молотком в кусок дерева, но нельзя забить гвоздь рукой?

См. решение

Проблема № 9

Стрелок оттягивает лук на 0,75 м, жесткость которого составляет 200 Н/м. Стрела весит 50 г. Какова скорость стрелы сразу после выпуска?

См. решение

Проблема № 10

Когда движущийся автомобиль сталкивается с льдиной, включаются тормоза. Почему желательно, чтобы колеса катились по льду без блокировки?

См. решение

Решения для вопросов по физике для старших классов

Решение проблемы № 1

Нет. Если объект тяжелее, сила тяжести больше, но поскольку он имеет большую массу, ускорение такое же, поэтому он движется с той же скоростью (если пренебречь сопротивлением воздуха). Если мы посмотрим на второй закон Ньютона, F = мА. Сила тяжести равна F = мг , где м — масса объекта, а г — ускорение свободного падения.

Приравнивая, имеем мг = ма. Следовательно, а = g .

Если бы не было сопротивления воздуха, перо падало бы с той же скоростью, что и яблоко.

Решение проблемы № 2

Если бы объект был полностью погружен в более плотную жидкость, результирующая выталкивающая сила превысила бы вес объекта. Это связано с тем, что вес жидкости, вытесненной объектом, больше веса объекта (поскольку жидкость более плотная). В результате объект не может оставаться полностью погруженным и плавает. Научное название этого явления — 9.0889 Принцип Архимеда .

Решение проблемы № 3

Не ограничивая общности, нам нужно только взглянуть на уравнение для положения x , поскольку мы знаем, что центростремительное ускорение указывает на центр окружности. Таким образом, когда θ = 0, вторая производная x по времени должна быть центростремительным ускорением.

Первая производная от x по времени t равна:

dx/dt = — Rsinθ (d θ /d t )

Вторая производная от x по времени t равна:

d 2 x/dt 2 = — Rcosθ (d θ /d t ) 2 − Rsinθ (d 2 θ /d t 2 )

В обоих приведенных выше уравнениях используется цепное правило исчисления, и по предположению θ является функцией времени. Следовательно, θ можно дифференцировать по времени.

Теперь оцените вторую производную при θ = 0.

У нас есть,

D 2 X /DT 2 = — R (D θ /D T ) 2

Термин D 0) 2

угловая скорость, которая является скоростью изменения угла θ . Он измеряется в радианах в секунду.

Для удобства можно установить w ≡ d θ /d t .

Следовательно,

d 2 x/dt 2 = — R w 2

Это хорошо известная форма уравнения центростремительного ускорения.

Решение проблемы № 4

Причина, по которой вы чувствуете себя невесомым, заключается в том, что на вас не действует никакая сила, поскольку вы ни с чем не соприкасаетесь. Гравитация одинаково притягивает все частицы вашего тела. Это создает ощущение, что на вас не действуют никакие силы, и вы чувствуете себя невесомым. Это было бы такое же ощущение, как если бы вы парили в космосе.

Решение проблемы № 5

Центростремительное ускорение — это ускорение, которое испытывает объект при движении с определенной скоростью по дуге. Центростремительное ускорение направлено к центру дуги.

Центробежная сила — это воображаемая сила, которую испытывает неограниченный объект при движении по дуге. Эта сила действует против направления центростремительного ускорения. Например, если автомобиль делает крутой поворот направо, пассажиры будут склонны соскальзывать на своих сиденьях от центра поворота влево (то есть, если они не пристегнуты ремнями безопасности). Пассажирам будет казаться, что они испытывают силу. Это определяется как центробежная сила.

Решение проблемы № 6

Мощность — скорость выработки или потребления энергии. Например, если двигатель производит 1000 ватт мощности (где ватты — это джоули в секунду), то через час общая энергия, производимая двигателем, составляет 1000 джоулей в секунду × 3600 секунд = 3 600 000 джоулей.

Решение проблемы № 7

Ответ (а).

Так как столкновение лобовое, и все автомобили идентичны и движутся с одинаковой скоростью, сила удара, испытываемого каждым автомобилем, одинакова и противоположна. Это означает, что удар такой же, как удар о сплошную стену на скорости 100 км/ч.

Решение проблемы № 8

Когда вы взмахиваете молотком, вы увеличиваете его кинетическую энергию, так что к тому времени, когда он ударяет по гвоздю, он придает большую силу, которая вбивает гвоздь в дерево.

Молоток — это, по сути, резервуар энергии, в который вы добавляете энергию во время замаха и который сразу высвобождается при ударе. Это приводит к тому, что сила удара значительно превышает максимальную силу, которую вы можете приложить, просто надавив на гвоздь.

Решение проблемы № 9

Эту проблему можно решить энергетическим методом.

Мы можем решить это, приравняв потенциальную энергию лука к кинетической энергии стрелы.

Дужку можно рассматривать как разновидность пружины. Потенциальная энергия пружины равна:

(1/2) k x 2 , где k — жесткость, а x — степень растяжения или сжатия пружины.

Следовательно, потенциальная энергия PE лука это:

ПЭ = (1/2)(200)(0,75) 2 = 56,25 Дж

Кинетическая энергия частицы равна:

(1/2) м v 2 , где м — масса, а v — скорость.

Стрелу можно рассматривать как частицу, поскольку она не вращается после выпуска.

Следовательно, кинетическая энергия KE стрелы равна:

КЭ = (1/2)(0,05) v 2

Если предположить, что энергия сохраняется, то

ПЭ = КЭ

Решая скорость стрелы v получаем

v = 47,4 м/с

Решение проблемы № 10

Статическое трение больше кинетического.

Статическое трение существует, если колеса продолжают катиться по льду без блокировки, что приводит к максимальному тормозному усилию. Однако, если колеса блокируются, кинетическое трение берет верх, поскольку между колесом и льдом возникает относительное проскальзывание. Это снижает тормозное усилие, и автомобилю требуется больше времени для остановки.

Антиблокировочная тормозная система (ABS) автомобиля предотвращает блокировку колес при торможении, что сводит к минимуму время, необходимое для полной остановки автомобиля. Кроме того, предотвращая блокировку колес, вы лучше контролируете автомобиль.

Вопросы по физике для колледжей и университетов (в основном для первого курса)

Проблемы плотности
Проблемы с энергией
Проблемы с силой
Проблемы с трением
Проблемы с наклонной плоскостью
Проблемы с кинематикой
Проблемы с кинетической энергией
Проблемы с механикой
Проблемы импульса
Проблемы со шкивом
Проблемы со статикой
Проблемы термодинамики
Проблемы с крутящим моментом

Дополнительные сложные вопросы по физике

Приведенные ниже 20 вопросов по физике одновременно интересны и очень сложны. Скорее всего, вам придется потратить некоторое время, чтобы разобраться с ними. Эти вопросы выходят за рамки типичных задач, которые вы можете найти в учебнике по физике. В некоторых из этих вопросов по физике используются разные концепции, поэтому (по большей части) не существует единой формулы или набора уравнений, которые можно использовать для их решения. В этих вопросах используются концепции, преподаваемые в средней школе и колледже (в основном на первом курсе).

Рекомендуется упорно отвечать на эти вопросы по физике, даже если вы застряли. Это не гонка, поэтому вы можете проходить их в своем собственном темпе. В результате вы будете вознаграждены более глубоким пониманием физики.

Проблема № 1

Ниже показан кривошипно-шатунный механизм. Рычажный механизм BC длиной L соединяет маховик радиусом r (вращающийся вокруг фиксированной точки A ) с поршнем в точке C , который скользит вперед и назад в полом валу. Переменный крутящий момент T приложен к маховику таким образом, что он вращается с постоянной угловой скоростью. Покажите, что при одном полном обороте маховика энергия сохраняется для всей системы; состоящий из маховика, рычажного механизма и поршня (при отсутствии трения).

Обратите внимание, что гравитация г действует вниз, как показано на рисунке.

Несмотря на то, что энергия сохраняется для системы, почему лучше сделать компоненты приводного механизма максимально легкими (за исключением маховика)?

Проблема № 2

В двигателе используются пружины сжатия для открытия и закрытия клапанов с помощью кулачков. При жесткости пружины 30 000 Н/м и массе пружины 0,08 кг при какой максимальной частоте вращения двигателя не происходит «плавание клапанов»?

Во время цикла двигателя пружина сжимается от 0,5 см (клапан полностью закрыт) до 1,5 см (клапан полностью открыт). Предположим, что распределительный вал вращается с той же скоростью, что и двигатель.

Плавающие клапаны возникают, когда обороты двигателя достаточно высоки, так что пружина начинает терять контакт с кулачком при закрытии клапана. Другими словами, пружина не растягивается достаточно быстро, чтобы поддерживать контакт с кулачком, когда клапан закрывается.

Для простоты можно предположить, что к пружине применяется закон Гука, где сила, действующая на пружину, пропорциональна степени ее сжатия (независимо от динамических эффектов).

Вы можете игнорировать гравитацию в расчетах.

Проблема № 3

Объект движется по прямой. Его ускорение определяется выражением

где C — константа, n — действительное число, а t — время.

Найдите общие уравнения для положения и скорости объекта в зависимости от времени.

Проблема № 4

В стрельбе из лука выпущенная стрела может колебаться во время полета. Если мы знаем положение центра масс стрелки ( G ) и форму стрелки в момент ее колебания (показано ниже), мы можем определить расположение узлов. Узлы — это «стационарные» точки на стрелке, когда она колеблется.

Используя геометрический аргумент (без уравнений), определите расположение узлов.

Предположим, что стрела колеблется в горизонтальной плоскости, так что на стрелу в плоскости колебаний не действуют никакие внешние силы.

Проблема № 5

Колесо гироскопа вращается с постоянной угловой скоростью w s при прецессии вокруг вертикальной оси с постоянной угловой скоростью w p . Расстояние от оси вращения до центра передней грани вращающегося колеса гироскопа равно L , а радиус колеса r . Стержень, соединяющий шарнир с колесом, образует с вертикалью постоянный угол θ .

Определите компоненты ускорения, перпендикулярные колесу, в точках A, B, C, D, отмеченных, как показано на рисунке.

Проблема № 6

Когда автомобиль делает поворот, два передних колеса описывают две дуги, как показано на рисунке ниже. Колесо, обращенное внутрь поворота, имеет угол поворота больше, чем у внешнего колеса. Это необходимо для того, чтобы оба передних колеса плавно описывали две дуги, имеющие один и тот же центр, иначе при повороте передние колеса будут скользить по земле.

Во время поворота задние колеса обязательно описывают те же дуги, что и передние колеса? Основываясь на вашем ответе, каковы последствия поворота рядом с бордюром?

Проблема № 7

Горизонтальный поворотный стол на промышленном предприятии непрерывно подает детали в паз (показан слева). Затем он сбрасывает эти детали в корзину (показана справа). Между этими двумя ступенями поворотный стол поворачивается на 180°. Проигрыватель ненадолго останавливается на каждой 1/8 -й хода, чтобы получить новую деталь в слот слева.

Если скорость вращения поворотного стола составляет w радиан/сек, а внешний радиус поворотного стола равен R 2 , каким должен быть внутренний радиус R 1 , чтобы детали выпадали слота и в корзину, как показано на рисунке?

Предположим:

• Угловую скорость w поворотного стола можно считать постоянной и непрерывной; что означает, что вы можете игнорировать короткие остановки, которые проигрыватель делает на каждой 1/8 -й оборота.

• Корзина расположена под углом 180° к месту подачи.

• Пазы очень хорошо смазаны, поэтому трение между пазом и деталью отсутствует.

• Детали можно рассматривать как частицы, что означает, что вы можете игнорировать их размеры при расчете.

• Прорези совмещены с радиальным направлением поворотного стола.

Проблема № 8

Маховик однопоршневого двигателя вращается со средней скоростью 1500 об/мин. За пол-оборота маховик должен поглотить 1000 Дж энергии. Если максимально допустимое колебание скорости составляет ± 60 об/мин, какова минимальная инерция вращения маховика? Предположим, что трения нет.

Проблема № 9

Процесс экструзии алюминия моделируется численно с помощью компьютера. В этом процессе пуансон проталкивает алюминиевую заготовку диаметром D через матрицу меньшего диаметра d . При компьютерном моделировании какова максимальная скорость штампа V p , чтобы результирующая динамическая сила (предсказанная моделированием), действующая на алюминий во время экструзии, составляла не более 5% силы, вызванной деформацией алюминия? Оценить для конкретного случая, когда D = 0,10 м, d = 0,02 м, а плотность алюминия ρ = 2700 кг/м 3 .

Сила деформации алюминия во время экструзии определяется выражением

Подсказка:

Экструзия алюминия через фильеру аналогична протеканию жидкости по трубе с переходом от большего диаметра к меньшему (например, вода, протекающая через пожарный шланг). Чистая динамическая сила, действующая на жидкость, представляет собой результирующую силу, необходимую для ускорения жидкости, которая возникает, когда скорость жидкости увеличивается по мере ее перетекания из секции большего диаметра в секцию меньшего диаметра (из-за сохранения массы).

Проблема № 10

Ребенок на горизонтальной карусели сообщает мячу начальную скорость V отн . Найдите начальное направление и скорость V rel мяча относительно карусели так, чтобы относительно ребенка мяч вращался по идеальному кругу, пока он сидит на карусели. Предположим, что трения между каруселью и мячом нет.

Карусель вращается с постоянной угловой скоростью w радиан/сек, и мяч вылетает в радиусе r от центра карусели.

Проблема № 11

Тяжелый корпус насоса массой м необходимо поднять с земли с помощью крана. Для простоты движение предполагается двухмерным, а корпус насоса представлен прямоугольником с размерами сторон ab (см. рисунок). Трос длиной L 1 крепится к крану (в точке P ) и корпус насоса (в точке O ). Кран тянет вертикально на тросе с постоянной скоростью V p .

Предполагается, что центр масс G корпуса насоса находится в центре прямоугольника. Находится на расстоянии L 2 от точки O . Правая сторона корпуса насоса расположена на расстоянии c по горизонтали от вертикальной линии, проходящей через точку .Р .

Найти максимальное натяжение троса при подъеме, которое включает часть подъема до отрыва корпуса насоса от земли и после отрыва корпуса насоса от земли (отрыв). На этом этапе корпус насоса качается вперед и назад.

Оценка для конкретного случая, когда:

и = 0,4 м

б = 0,6 м

с = 0,2 м

Д 1 = 3 м

м = 200 кг

I G = 9 кг-м 2 (инерция корпуса насоса около G )

Предположим:

• Трение между корпусом насоса и землей достаточно велико, чтобы корпус насоса не скользил по земле (вправо) до отрыва.

• До отрыва динамические эффекты незначительны.

• Скорость V p достаточно высока, чтобы нижняя часть корпуса насоса отрывалась от земли после отрыва.

• Для аппроксимации натяжения троса можно смоделировать систему как обычный маятник во время раскачивания (можно игнорировать эффекты двойного маятника).

• Массой кабеля можно пренебречь.

Проблема № 12

Схема соединения показана ниже. Шарнирные соединения O 1 и O 2 прикреплены к стационарному основанию и разделены расстоянием b . Связи одинакового цвета имеют одинаковую длину. Все звенья соединены штифтами и допускают вращение. Определить путь, пройденный конечной точкой P , так как синяя тяга длиной b вращается вперед и назад.

Чем интересен этот результат?

Проблема № 13

Агрегат, несущий конвейерную ленту, показан на рисунке ниже. Двигатель вращает верхний ролик с постоянной скоростью, а остальные ролики могут вращаться свободно. Лента наклонена под углом θ . Чтобы удерживать ремень в натянутом состоянии, к ремню подвешен груз массой м , как показано на рисунке.

Найдите точку максимального натяжения ремня. Вам не нужно его вычислять, просто найдите место и объясните причину.

Проблема № 14

Проверка качества показала, что рабочее колесо насоса слишком тяжелое с одной стороны на величину, равную 0,0045 кг-м. Для исправления этого дисбаланса рекомендуется вырезать канавку по внешней окружности рабочего колеса с помощью фрезерного станка на той же стороне, что и дисбаланс. Это удалит материал с целью исправления дисбаланса. Размер канавки составляет 1 см в ширину и 1 см в глубину. Канавка будет симметрична относительно тяжелой точки. На каком расстоянии по внешней окружности рабочего колеса должна быть канавка? Укажите ответ в цифрах θ . Совет: рассматривайте канавку как тонкое кольцо материала.

Внешний радиус рабочего колеса в месте расположения канавки составляет 15 см.

Материал рабочего колеса – сталь плотностью ρ = 7900 кг/м 3 .

Проблема № 15

В рамках проверки качества осесимметричный контейнер помещается на очень хорошо смазанный фиксированный стержень, как показано ниже. Затем контейнер получает начальное чистое вращение w , без начального поступательного движения. Что вы ожидаете увидеть, если центр масс контейнера смещен от геометрического центра O контейнера?

Проблема № 16

Струя падающего материала ударяется о пластину ударного веса, и датчик горизонтальной силы позволяет рассчитать массовый расход. Если скорость материала непосредственно перед ударом о пластину равна скорости материала сразу после удара о пластину, определите уравнение для массового расхода материала на основе показаний датчика горизонтальной силы. Трением о пластину пренебречь.

Подсказка: это можно рассматривать как проблему с потоком жидкости.

Проблема № 17

SunCatcher — двигатель Стирлинга, работающий на солнечной энергии. Он использует большие параболические зеркала для фокусировки солнечного света на центральный приемник, который приводит в действие двигатель Стирлинга. В параболическом зеркале можно увидеть отражение пейзажа. Почему отражение вверх ногами?

Источник: http://www.stirlingenergy.com

Проблема № 18

В холодный и сухой зимний день ваши очки запотевают, когда вы входите в помещение после того, как какое-то время пробыли на улице. Почему это?

А если выйти на улицу с запотевшими очками, они быстро прояснятся.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *