Умножение 3 дробей с разными знаменателями: Умножение обыкновенных дробей — урок. Математика, 6 класс.

Содержание

Sitemap

SitemapГлавная

Умножение обыкновенных дробей
Деление обыкновенных дробей
Дробные выражения
Взаимно обратные числа
Нахождение числа по его дроби
Нахождение дроби от числа
Применение распределительного свойства умножения
Основное свойство дроби (Терентьева И.Г.)
Приведение дробей к общему знаменателю (Москаленко М.В)
Сравнение дробей с разными знаменателями
Основное свойство дроби (Богданович Е.М.)
Приведение дробей к общему знаменателю (Терентьева И.Г.)
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей
Основное свойство дроби (Слупко М.В.)
Сокращение дробей
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю (Слупко М.В.)
Масштаб (Вольфсон Г.И.)
Прямая и обратная пропорциональные зависимости
Шар
Длина окружности. Площадь круга (Вольфсон Г.И.)
Пропорции (Вольфсон Г.И.)
Изменение площадей и объёмов
Отношения
Пропорции (Слупко М.В.)
Масштаб (Слупко М.

В.)
Длина окружности. Площадь круга (Слупко М.В.)
Признаки делимости на 9 и на 3
Наименьшее общее кратное (Богданович Е.М.)
Наибольший общий делитель. Алгоритм Евклида
Разложение числа на множители
Наименьшее общее кратное (Вольфсон Г.И.)
Простые и составные числа
Признаки делимости на 10, на 5 и на 2
Делители и кратные
Наибольший общий делитель. Наименьшее общее кратное. Часть 1. НОД (Слупко М.В.)
Наибольший общий делитель. Наименьшее общее кратное. Часть 2. НОК (Слупко М.В.)
Параллельные и перпендикулярные прямые
Координатная плоскость
Столбчатые диаграммы
Графики
Деление
Свойства действий с рациональными числами
Рациональные числа
Умножение положительных и отрицательных чисел
Приведение подобных слагаемых (Вольфсон Г.И.)
Раскрытие скобок
Решение уравнений (Вольфсон Г.И.)
Коэффициент
Приведение подобных слагаемых (Слупко М.В.)
Решение уравнений (Слупко М.В.)
Вычитание
Сложение чисел с помощью координатной прямой
Сложение отрицательных чисел
Сложение чисел с разными знаками
Отрицательные числа.

Противоположные числа (Слупко М.В.)
Модуль числа
Сравнение чисел
Координаты на прямой
Изменение величин
Отрицательные числа (Вольфсон Г.И.)
Делители и кратные. Простые и составные числа. Часть 1. Простые и составные числа
Делители и кратные. Простые и составные числа. Часть 1. Простые и составные числа (альтернативный урок)
Делители и кратные. Простые и составные числа. Часть 2. Разложение числа на простые множители
Делители и кратные. Простые и составные числа. Часть 3. Делитель и кратное
Признаки делимости. Часть 1. Делимость чисел
Признаки делимости. Часть 2. Делимость суммы и признак делимости на 2, 5 и 10
Признаки делимости. Часть 3. Признак делимости на 3 и 9
Признаки делимости. Часть 4. Практика. Применение нескольких признаков делимости
Разложение числа на простые множители. Часть 1. Необходимость умения раскладывать числа на множители. Примеры 1 и 2
Разложение числа на простые множители. Часть 2. Пример 3. Разложение числа 1225 на простые множители
Разложение числа на простые множители.

Часть 3. Пример 4. Разложение числа 45630 на простые множители
НОД. Свойства НОД. Алгоритм Евклида. Часть 1. Наибольший общий делитель
НОД. Свойства НОД. Алгоритм Евклида. Часть 1. Определение НОД (альтернативный урок)
НОД. Свойства НОД. Алгоритм Евклида. Часть 1. Вычисление НОД (альтернативный урок)
НОД. Свойства НОД. Алгоритм Евклида. Часть 2. Свойства НОД
НОД. Свойства НОД. Алгоритм Евклида. Часть 3. Решение примеров
НОД. Свойства НОД. Алгоритм Евклида. Часть 4. Алгоритм Евклида
НОК. Свойства НОК Контрольная работа. Часть 1. Наименьшее общее кратное
НОК. Свойства НОК Контрольная работа. Часть 1. НОК и его свойства (альтернативный урок)
НОК. Свойства НОК Контрольная работа. Часть 2. Вычисление НОК двух и более чисел
НОК. Свойства НОК Контрольная работа. Часть 3. Связь между НОК и НОД
Основное свойство дроби. Сокращение дробей. Часть 1. Изменение дроби при увеличении/уменьшении ее числителя
Основное свойство дроби. Сокращение дробей.

Часть 2. Изменение дроби при увеличении/уменьшении ее знаменателя
Основное свойство дроби. Сокращение дробей. Часть 3. Основное свойство дроби
Основное свойство дроби. Сокращение дробей. Часть 4. Сокращение дробей
Основное свойство дроби. Сокращение дробей. Часть 5. Задачи на сокращение дробей
Основное свойство дроби. Сокращение дробей. Часть 6. Задача на доказательство
Приведение дробей к общему знаменателю. Часть 1. Приведение дробей к общему знаменателю с помощью эквивалентных дробей
Приведение дробей к общему знаменателю. Часть 2. Приведение дробей к общему знаменателю с помощью перемножения знаменателей
Приведение дробей к общему знаменателю. Часть 3. Наименьший общий знаменатель
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей. Часть 1. Сложение дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей. Часть 2. Вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями.

Сравнение дробей. Часть 3. Решение примеров
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей. Часть 4. Сложение и вычитание смешанных чисел
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей. Часть 5. Вычитание правильной дроби из целого числа. Решение примеров
Умножение дробей. Часть 1. Умножение обыкновенных дробей
Умножение дробей. Часть 2. Умножение смешанных чисел
Умножение дробей. Часть 3. Решение задач
Умножение дробей. Часть 4. Распределительный закон умножения. Умножение смешанной дроби на целое число
Умножение дробей. Часть 5. Решение примеров
Взаимно обратные числа. Деление дробей. Часть 1. Взаимно обратные числа. Нахождение числа, обратного данному
Взаимно обратные числа. Деление дробей. Часть 2. Свойства взаимно обратных чисел
Взаимно обратные числа. Деление дробей. Часть 3. Правило деления обыкновенных дробей
Взаимно обратные числа. Деление дробей. Часть 4. Решение примеров
Взаимно обратные числа.

Деление дробей. Часть 5. Задача на деление обыкновенных дробей
Нахождение дроби от числа. Нахождение числа по заданному значению его дроби. Часть 1. Нахождение дроби от числа
Нахождение дроби от числа. Нахождение числа по заданному значению его дроби. Часть 2. Нахождение процента от числа
Нахождение дроби от числа. Нахождение числа по заданному значению его дроби. Часть 3. 1 тип задач: нахождение дроби от числа
Нахождение дроби от числа. Нахождение числа по заданному значению его дроби. Часть 4. 2 тип задач: нахождение числа по его дроби
Нахождение дроби от числа. Нахождение числа по заданному значению его дроби. Часть 5. 3 тип задач: нахождение процентного отношения двух чисел
Дробные выражения. Часть 1. Упрощение дробных выражений
Дробные выражения. Часть 2. Решение более сложных примеров
Дробные выражения. Часть 3. Дробные выражения с переменными
Отношения. Часть 1. Отношение чисел
Отношения. Часть 2. Решение задач
Пропорции. Масштаб.

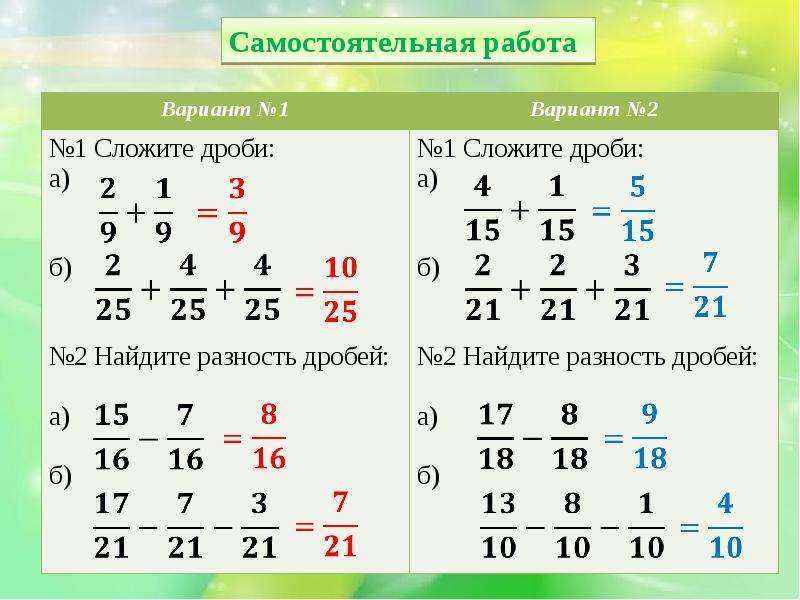Контрольная работа. Часть 1. Пропорции и их свойства
Пропорции. Масштаб. Контрольная работа. Часть 2. Решение задач на пропорции
Пропорции. Масштаб. Контрольная работа. Часть 3. Масштаб и его виды
Пропорции. Масштаб. Контрольная работа. Часть 4. Решение задач на масштаб
Прямая и обратная пропорциональные зависимости. Изменение площадей и объемов. Часть 1. Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости. Изменение площадей и объемов. Часть 2. Решение задач
Прямая и обратная пропорциональные зависимости. Изменение площадей и объемов. Часть 3. Формула прямо пропорциональной зависимости
Прямая и обратная пропорциональные зависимости. Изменение площадей и объемов. Часть 4. Изменение площади
Прямая и обратная пропорциональные зависимости. Изменение площадей и объемов. Часть 5. Изменение объема
Отрицательные числа. Изменение величин. Часть 1. Отрицательные числа, противоположные числа, ноль
Отрицательные числа.

Изменение величин. Часть 2. Нахождение противоположного числа. Множества целых и натуральных чисел
Отрицательные числа. Изменение величин. Часть 3. Изменение величин
Координаты на прямой. Часть 1. Координатная прямая. Координаты точки
Координаты на прямой. Часть 2. Использование координатной прямой
Модуль числа. Сравнение чисел. Часть 1. Модуль числа
Модуль числа. Сравнение чисел. Часть 2. Решение примеров
Модуль числа. Сравнение чисел. Часть 3. Правила сравнения чисел
Модуль числа. Сравнение чисел. Часть 4. Решение примеров
Шар. Часть 1. Шар, сфера и их изображение
Шар. Часть 2. Площадь поверхности и объем шара
Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Часть 1. Сложение и вычитание чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Часть 2. Решение примеров
Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Часть 3.

Сложение отрицательных чисел
Сложение чисел с разными знаками. Вычитание. Часть 1. Отрицательные и противоположные числа
Сложение чисел с разными знаками. Вычитание. Часть 2. Сложение с отрицательными числами
Сложение чисел с разными знаками. Вычитание. Часть 3. Вычитание чисел
Умножение и деление положительных и отрицательных чисел. Часть 1. Умножение положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел. Часть 2. Деление положительных и отрицательных чисел
Рациональные числа. Часть 1. Множество рациональных чисел
Рациональные числа. Часть 2. Обыкновенные и десятичные дроби
Свойства действий с рациональными числами. Контрольная работа. Часть 1. Свойства арифметических действий с числами
Свойства действий с рациональными числами. Контрольная работа. Часть 2. Сложение и умножение рациональных чисел
Окружность и круг. Часть 1. Окружность
Окружность и круг. Часть 2. Круг
Окружность и круг. Часть 2.

Задача (альтернативный урок)
Окружность и круг. Часть 1. Окружность, круг и их элементы (альтернативный урок)
Длина окружности и площадь круга. Часть 1. Длина окружности
Длина окружности и площадь круга. Часть 2. Площадь круга
Раскрытие скобок. Часть 1. Раскрытие скобок, перед которыми стоит знак плюс
Раскрытие скобок. Часть 2. Решение примеров
Раскрытие скобок. Часть 3. Раскрытие скобок, перед которыми стоит знак минус
Раскрытие скобок. Часть 4. Решение примеров
Коэффициент. Приведение подобных слагаемых. Часть 1. Коэффициент
Коэффициент. Приведение подобных слагаемых. Часть 2. Приведение подобных слагаемых
Коэффициент. Приведение подобных слагаемых. Часть 3. Решение примеров
Решение уравнений. Часть 1. Эквивалентные уравнения. Перенос слагаемых
Решение уравнений. Часть 2. Решение уравнений. Домножение и деление
Перпендикулярные прямые. Параллельные прямые. Часть 1. Перпендикулярные прямые
Перпендикулярные прямые. Параллельные прямые.

Часть 2. Параллельные прямые
Координатная плоскость. Часть 1. Координатная плоскость. Координаты точки
Координатная плоскость. Часть 2. Решение задач
Диаграммы. Часть 1. Круговая диаграмма и ее построение
Диаграммы. Часть 2. Решение задачи
Диаграммы. Часть 4. Решение задач
Диаграммы. Часть 3. Столбчатая диаграмма и ее построение
Графики. Контрольная работа. Часть 1. Графики
Графики. Контрольная работа. Часть 2. Решение задач

Деление дробей с разными знаменателями – примеры и правила (5 класс, математика)

4.6

Средняя оценка: 4.6

Всего получено оценок: 261.

4.6

Средняя оценка: 4.6

Всего получено оценок: 261.

Дроби неприятны тем, что большое воздействие на действия с ними оказывают знаменатели. Часто ученики 5 класса приходят в ступор при виде дробей с разными знаменателями, начиная выполнять, лишние действия и терять время. А ведь не для всех действий с дробями требуется наличие одинакового знаменателя, поговорим подробнее о данном вопросе.

Действия с дробями

Необходимость приведения к одному знаменателю зависит от выполняемых действий. Разобьем возможные действия на группы и разберемся с каждой из групп в отдельности.

Сложение и вычитание

Сложение и вычитание дробей основано на вынесении общего множителя. Рассмотрим на примере, как выглядит сложение дробей в подробности:

$${3\over{13}}+{5\over{13}}={1\over{13}}*(3+5)={8\over{13}}$$

Это значит, что сложение и вычитание дробей возможно только при условии наличия одинакового знаменателя. Если знаменатели у дробей разные, то необходимо привести дроби к общему знаменателю.

Если не привести дроби к одному знаменателю, то общий множитель просто не получится вынести, а принцип сложение осуществить не получится. Поэтому вычитание или сложение дробей с разными знаменателями невозможно. Это непреложное правило.

Умножение

Умножение дробей не требовательно к знаменателю. Здесь используется совершенно иной принцип. Дело в том, что дробную черту можно заменить знаком деления. Тогда:

${3\over{5}}*{2\over{3}}=3:5*2:3=(3*2):(5*3)={6\over{15}}$ – для того, чтобы перемножить две дроби нужно умножить числитель на числитель, а знаменатель на знаменатель. Получившаяся дробь будет результатом умножения.

Деление

Деление использует те же принципы, что и умножение:

${3\over{5}}:{2\over{3}}=(3:5):(2:3)=3:5*3:2=9:10={9\over{10}}$ – для того, чтобы разделить одну дробь на другую необходимо перевернуть дробь-делитель. Для этого числитель меняется на знаменатель, а знаменатель на числитель. После этого делимое и перевернутый делитель необходимо перемножить. Результат умножение будет результатом деления изначальных чисел.

Одинаковый знаменатель ни для деления, ни для умножения дробей не требуется. Помните, что каждое действие в математике имеет свое основание.

Основанием для сложения и умножения является общий множитель. Значит нужно, чтобы этот общий множитель был. Поэтому требуется одинаковый знаменатель у двух дробей. Основание для деления и умножения – математический смысл дроби.

Этот принцип работает вне зависимости от значения знаменателя, поэтому деление дробей с разными знаменателями и деление дробей с одинаковым знаменателем не отличается. Последовательность действий при решении примеров деления дробей с разными знаменателями одна и та же.

Что мы узнали?

Мы поговорили о действиях с дробями. Выделили отдельные группы действий с дробями. Привели обоснование каждому из действий. Объяснили, когда необходимо наличие одинакового знаменателя, а когда нет. Отдельно рассмотрели деление дробей с разными знаменателями и сказали, что это действие возможно с любыми знаменателями дробей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 261.

А какая ваша оценка?

Как сложить 3 дроби с разными знаменателями?

Дроби могут быть определены как числа, которые могут быть представлены в виде A/B , где A и B — целые числа, а B не должно быть равно нулю. В дроби верхняя часть называется Числитель , а нижняя часть называется Знаменатель.

Примеры: 1/2, 4/5, -2/3 и т. д.

Сложение дробей

Для сложения дробей существует правило, согласно которому знаменатели складываемых дробей должны быть равны. . Если знаменатели дроби не равны, сделайте их равными, взяв наименьшее общее кратное (НОК) знаменателей.

Как найти LCM?

Чтобы найти НОК чисел (здесь знаменатели), мы будем использовать метод деления .

Давайте разберемся с этим методом на примере, возьмем два числа 6 и 15 для нахождения НОК методом деления.

Шаг 1: Составьте таблицу, состоящую из левой и правой частей, в правой части укажите числа, НОК которых мы находим.

Шаг 2: Теперь начните с наименьшего числа (не 1) и проверьте, имеет ли любое число из заданных чисел это кратное. В примере 2 — это множитель 6, поэтому используйте его, чтобы разделить 6 в следующей строке.

Шаг 3: Теперь во второй строке 3 осталось 15, только множитель 3 равен 3, поэтому разделите его на 3. 3 также является коэффициентом 15, так что разделите 15 также. В результате получается 1, 5.

Шаг 4: Теперь 5 является коэффициентом 5, поэтому делим 5, результат равен 1, 1.

Шаг 5: Процесс завершен, так как мы получаем 1 для всех чисел , теперь умножьте все числа в левой части, которые равны 2, 3, 5, так что кратное из них равно 30.

Сложение 3 дробей с разными знаменателями

Шаги для сложения дробей с разными знаменателями:

Шаг 1: Найдите НОК знаменателей.

Шаг 2: Разделите LCM на знаменатель каждого числа, которое необходимо добавить.

Шаг 3: Умножьте числитель на частное ( найденное на предыдущем шаге).

Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как при простом сложении.

Шаг 5: Знаменатель будет LCM.

Возьмем 3 дроби с разными знаменателями, 1/2, 2/3, 3/4

Шаг 1: Нахождение НОК 2,3,4

Шаг 2: Разделим НОК на знаменатель каждого числа, которое нужно сложить.

LCM = 12, поэтому разделите его на каждое число (знаменатель)

12/2 = 6 частное 1

12/3 = 4 частное 2

12/4 = 3 частное 3

3 3 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числители 1, 2, 3, поэтому умножьте их на соответствующие частные.
1×6 = 6
2×4 = 8
3×3 = 9
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
6 + 8 + 9 = 23, что является числителем.
Шаг 5: В знаменателе будет LCM, то есть 12.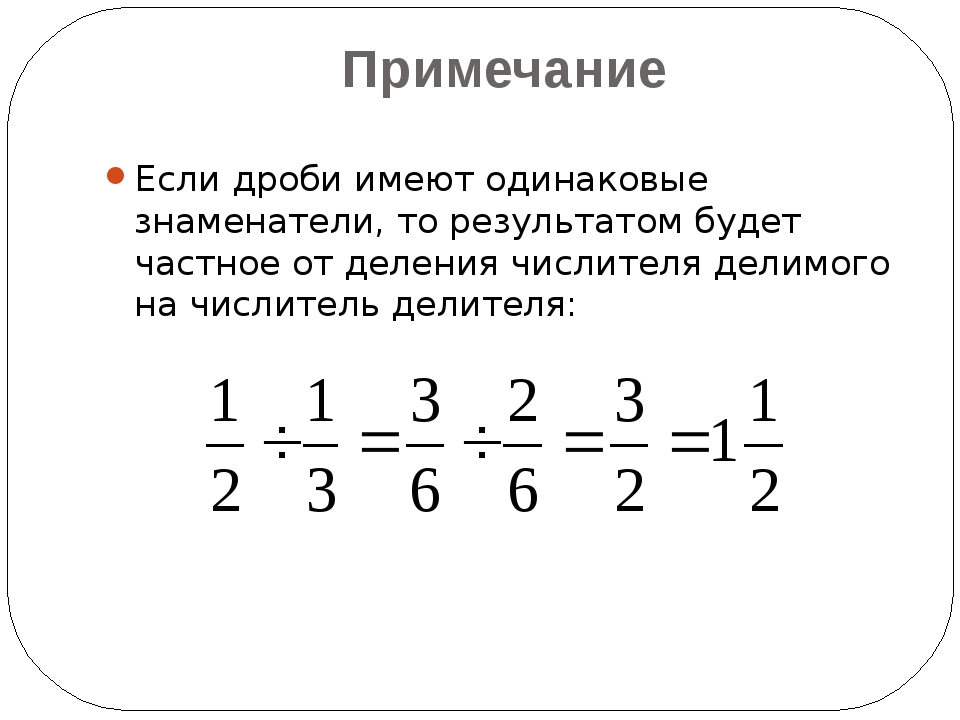
Ответ: 23/12

Метод перекрестного умножения , 3/4
Шаг 1: Возьмите две дроби за один раз, чтобы взять 1/2 и 2/3
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель первого числа второе число, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×3 + 2×2 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
2×3 = 6, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/6.
Шаг 5: Повторите описанную выше процедуру, взяв новую дробь 7/6 и третью дробь 3/4.
Наконец, мы получили ответ, который совпадает с найденным выше.
Примеры вопросов
Вопрос 1: Сложите указанные дроби 1/7, 2/7, 3/7.
Ответ:
В данном вопросе знаменатели равны, поэтому просто сложите числители, и знаменатель будет равен 7. 6/7.
Вопрос 2: Найдите LCM 7, 3, 12.
Ответ:
Вопрос 3: Добавьте данную фракции, 2/7, 5/12, 1. /3.
Ответ:
Шаг 1: Нахождение НОК 7,12,3
МОК, которое мы получили, равно 84.
Шаг 2: Разделите НОК каждого числа, которое нужно добавить, на знаменатель .
LCM = 84, поэтому разделите его на каждое число (знаменатель)
84/7 = 12 частное 1
84/12 = 7 частное 2
84/4 = 21 частное 3
2 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числитель 2, 5, 1, поэтому умножьте их на соответствующие частные.
2×12 = 24
5×7 = 35
1×21 = 21
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
24 + 35 + 21 = 80, что является числителем.
Шаг 5: В знаменателе будет НОК, то есть 84.
Ответ: 80/84
Вопрос 4: Сложите данные дроби, 4/5, 3/10, 1/3.
Ответ:
Шаг 1: Нахождение НОК 5,10,3
МОК, которое мы получили, равно 30. быть добавлено.
LCM = 30, поэтому разделите его на каждое число (знаменатель)
30/5 = 6 частное 1
30/10 = 3 частное 2
30/3 = 10 частное 3
2 2 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числители 4, 3, 1, поэтому умножьте их на соответствующие частные.
4×6 = 24
3×3 = 9
1×10 = 10
Шаг 4: Сложите числители, полученные после умножения на частные, как простое сложение.
24 + 9 + 10 = 43, что является числителем.
Шаг 5: Знаменатель будет LCM, поэтому будет 30.
Ответ: 43/30
Вопрос 5: Найдите LCM 7, 3, 12, 13
Ответ:
Вопрос 6: Сложите данные дроби 1/3, 1/4, 1/2 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмем две дроби за раз, так что возьмем 1/3 и 1/4 первое число со знаменателем второго числа, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×4 + 1×3 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
3×4 = 12, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/12.
Шаг 5: Снова возьмите 7/12 и третью дробь, которая равна 1/2.
Шаг 6: Нахождение числителя
7×2 + 1×12 = 26, что является числителем
Шаг 7: Нахождение знаменателя
12×2 = 24, что является знаменателем
9/2 теперь упростив его, мы получим 13/12.
Вопрос 7: Сложите данные дроби 1/5, 2/5, 3/10 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмите две дроби за один раз, так что возьмите 1/5 и 2/5
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель второго числа и аналогичным образом умножим числитель второго числа на знаменатель первого числа и сложим оба термина, чтобы получить числитель.
1×5 + 2×5 = 15, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
5×5 = 25, что является знаменателем.
Шаг 4: Находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь равна 15/25, при делении числителя и знаменателя на 5 получаем 3/5.
Шаг 5: Теперь возьмите 3/5 и третью дробь, которая равна 3/10.
Шаг 6: Нахождение числителя
3×10 + 3×5 = 45, что является числителем
Шаг 7: Нахождение знаменателя
10×5 = 50, что является знаменателем
Ответ 45/50 при делении числителя и знаменателя на 5 получаем 9/10.

Математическое выражение: умножение дробей
00:00:02.100
На этом уроке мы изучим основы умножения дробей.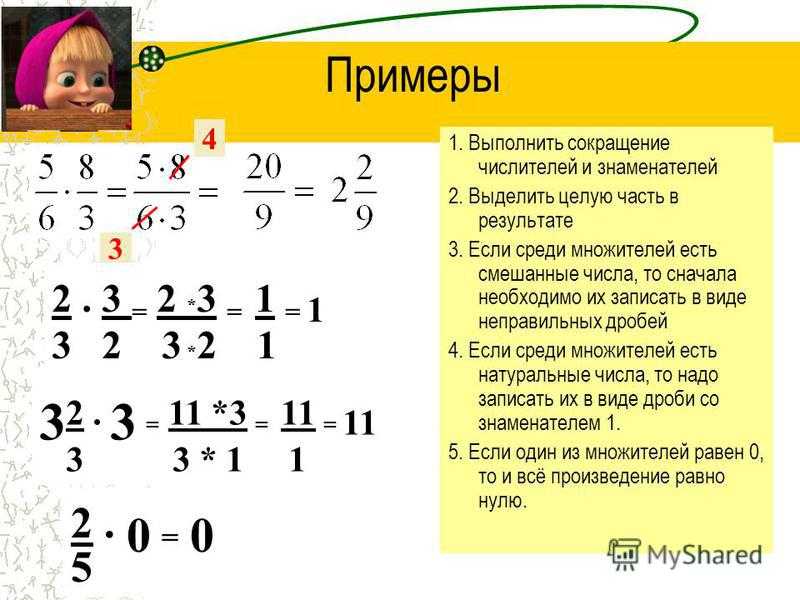

00:00:07.180
Теперь, по сравнению со сложением или вычитанием дробей, умножать дроби проще.
00:00:14.130
Это потому, что при умножении дробей нам не нужно делать знаменатели одинаковыми.
00:00:21.030
Например, умножим 2/3 на 4/5.
00:00:29.020
Для этого нам просто нужно перемножить числители.
00:00:34,190
Следовательно, мы умножаем 2 на 4. Это дает 8.
00:00:40,100
Затем мы умножаем знаменатели вместе.
00:00:44,130
Следовательно, мы умножаем 3 на 5. Это дает 15.
00:00:51,020
Итак, наконец, мы можем видеть, что это дробное умножение дает 8/15.
00:00:57.180
Теперь давайте наглядно рассмотрим, как работает это умножение дробей.
00:01:03.000
С помощью этого прямоугольника мы можем представить 2/3. Точно так же мы изображаем 4/5 с помощью этого прямоугольника.

00:01:13.130
Когда мы умножаем эти дроби визуально, это означает, что мы объединяем эти прямоугольники.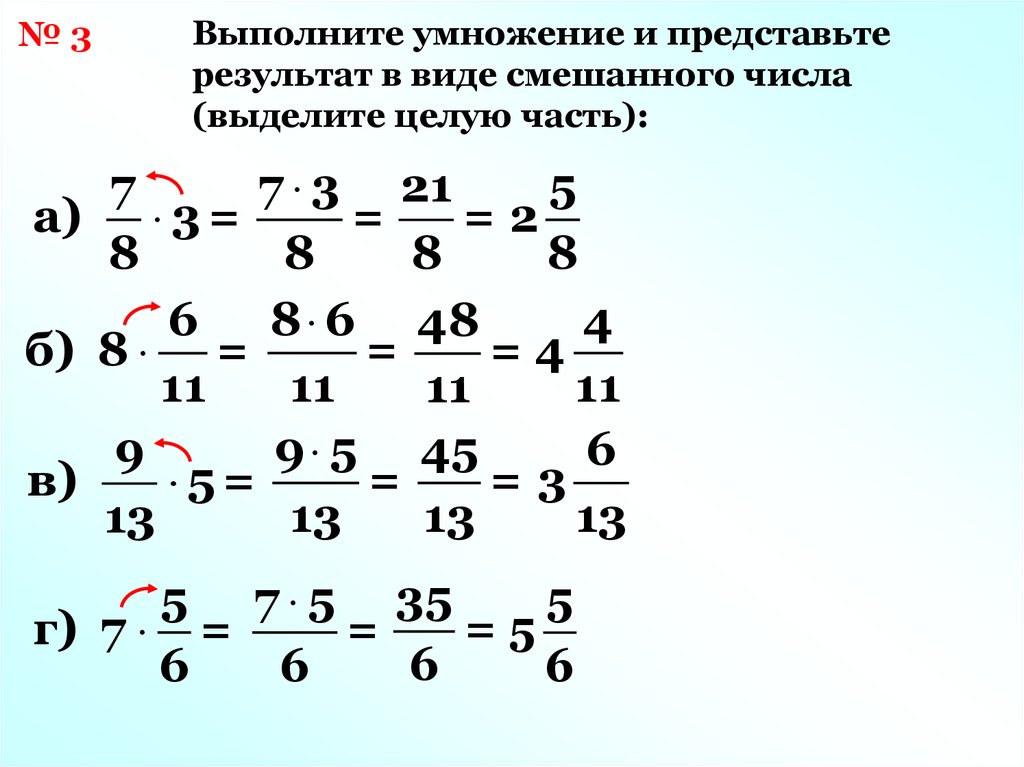
00:01:20.210
Когда зеленый и фиолетовый прямоугольники перекрываются, они дают синие прямоугольники.
00:01:26.090
Здесь мы видим, что эти 8 синих прямоугольников представлены числителем 8.
00:01:32.150
Также обратите внимание, что всего 15 прямоугольников, которые представлены знаменателем 15.
00:01:43.240
Хорошо, давайте посмотрим на другие примеры умножения дробей.
00:01:50.100
Умножим 7/8 на 2/5.
00:01:57.120
Сначала умножим числители. Итак, мы умножаем 7 на 2. Это дает 14.
00:02:12.030
Далее умножаем знаменатели. Итак, умножаем 8 на 5. Получается 40.
00:02:18.220
Теперь у нас есть дробь 14/40.
00:02:23.210
Обратите внимание, что мы можем упростить эту дробь. Для этого разделим числитель и знаменатель на 2.
00:02:32.070
Это дает упрощенную дробь 7/20.
00:02:38.120
Следующий пример, давайте умножим 1/3 на 3 1/2.
00:02:45. 080
Обратите внимание на смешанную дробь?
00:02:48.050
Перед умножением важно заменить его на неправильную дробь.
00:02:53.180
Для этого сначала умножим 2 на 3. Получится 6. числитель.
00:03:11.150
Следовательно, у нас есть неправильная дробь 7/2.
00:03:16.170
Теперь мы можем умножить эти дроби.
00:03:20.230
Сначала умножьте числители. Итак, мы умножаем 1 на 7. Это дает 7.
00:03:31.000
Далее умножаем знаменатели. Итак, мы умножаем 3 на 2. Это дает 6.
00:03:41.230
Обратите внимание, что 7/6 — неправильная дробь. Теперь, вместо того, чтобы оставлять ответ в таком виде, рекомендуется изменить его на смешанную дробь, используя длинное деление.

00:03:53.240
Вот как. 7/6 — это то же самое, что 7 делит 6. Теперь это деление дает частное 1. Это частное на самом деле является целым числом смешанной дроби.
00:04:11.160
Затем мы умножаем 1 на 6. Это дает 6. 7 минус 6 дает остаток как 1.