Умножение чисел. Множимое, множитель и произведение
- Множимое, множитель и произведение
- Проверка умножения
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
4 + 4 + 4 = 12.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х
(косой крест) или ·
(точка), который ставится между числами. Например:
4 х 3 или 4 · 3
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак =
(равно), после которого записывается полученный результат:
4 · 3 = 12.
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
6 + 6 + 6 + 6 + 6 = 30.
Сократим запись, заменив сложение на умножение:
6 · 5 = 30.
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 · 3,
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
4 · 3 = 12,
12 — это произведение.
При этом сама запись 4 · 3 тоже называется произведением.
Эту запись можно прочитать так: произведение четырёх и трёх равно двенадцати
, четыре умножить на три равно двенадцати
, по четыре взять три раза, получится двенадцать
.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Рассмотрим выражение:
4 · 3 = 12,
где 4 — это множимое, 3 — это множитель, а 12 — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:
- Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:
12 : 3 = 4.
- Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно: 12 : 4 = 3.
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Умножение | Математика
Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.
Определение умножения
Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.
Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.
Умножение есть сложение равных слагаемых.
Данные в умножении называются множимым и множителем, а искомое — произведением.
В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.
Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.
Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым.
Множитель показывает число равных слагаемых.
Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.
Множимое и множитель вместе называются производителями.
При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.
Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.
Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать
7 + 7 + 7
пишут при помощи знака умножения короче:
7 × 3 или 7 · 3
Умножение есть сокращенное сложение равных слагаемых.
Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).
Связь между данными и искомым числом выражается в умножении
письменно:
7 × 3 = 21 или 7 · 3 = 21
словесно:
семь, умноженное на три, составляет 21.
Чтобы составить произведение 21, нужно 7 повторить три раза
21 = 7 + 7 + 7
Чтобы составить множитель 3, нужно единицу повторить три раза
3 = 1 + 1 + 1
Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:
Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
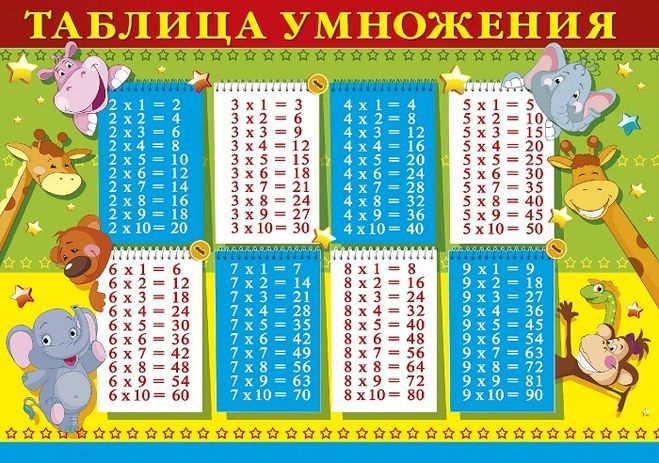
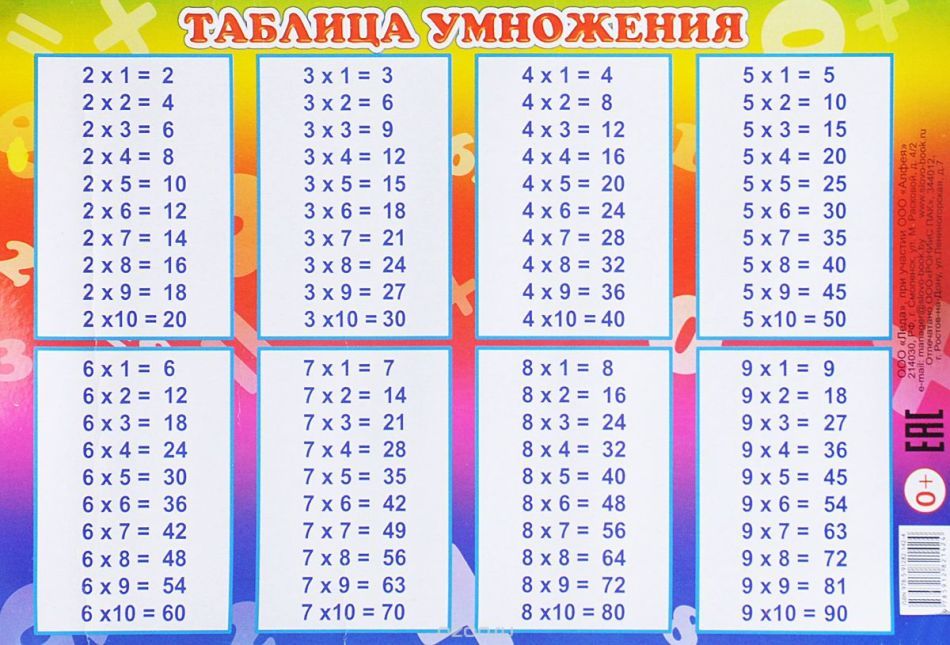
Умножение однозначных чисел. Таблица Пифагора
Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.
Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).
Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д.
Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.
Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде
Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.
Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:
Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.
Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых
следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:
Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
-
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
Умножение продолжается до тех пор, пока не получат полного произведения.
Умножение чисел на 10, 100, 1000 …
Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.
Этого достигают, приписывая к числу два нуля.
Отсюда заключаем:
Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.
Умножение числа 6035 на 1000 выразится письменно:
Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.
Умножение на число с нулями в конце
Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз.
Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.
Ход вычисления выразится письменно:
Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.
Умножение многозначного числа на многозначное
Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.
Три произведения
называются частными произведениями.
Полное произведение 3029 × 429 равно сумме трех частных:
3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.
Найдем величины этих трех частных произведений.
Умножая 3029 на 9, находим:
3029 × 9 27261 первое частное произведение
Умножая 3029 на 20, находим:
3029 × 20 60580 второе частное произведение
Умножая 3026 на 400, находим:
3029 × 400 1211600 третье частно произведение
Сложив эти частные произведения, получим произведение 3029 × 429:
Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.
Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:
В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры.
Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.
Отыскивая произведение 3247 на 209, имеем:
Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.
Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.
Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,
нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.
Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.
Пример. Найти произведение 342 на 2700.
Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.
Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35
Приписывая к 945 пять нулей, получаем искомое произведение:
2700 × 35000 = 94500000.
Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом.
Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.
В нашем произведении может содержаться или 7 или 6 цифр.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
2 × 2 = 4, 3 × 3 = 9.
Квадраты. Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы. Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями.
Произведения трех равных множителей или кубы называются третьими степенями, и т. д.
Что такое умножение?
Что такое умножение?
В той первоначальной публикации я отметил, что не стоит говорить студентам, что «умножение — это многократное сложение». Оказалось, что многие учителя думали, что это именно так, поэтому я был вынужден опубликовать то, что в итоге превратилось в три колонки, каждая из которых длиннее и глубже, чем предыдущая, объясняя, почему мем «умножение — это повторное сложение» ( MIRA) не только неправильна, но и опасна для распространения с точки зрения образования. Опасность была продемонстрирована в драматической форме большим объемом полученной мной корреспонденции и множеством последовавших за этим публичных тем в блогах, которые показали, что очень многие граждане горячо верят в MIRA.
Те из нас, кто преподает математику на любом уровне, просто не должны заниматься распространением лжи. Конечно, иногда мы говорим «не всю правду», чтобы предоставить нашим ученикам управляемый путь к овладению тем, что может быть трудным понятием. Но когда мы делаем это, у нас есть обязательство (1) не говорить вопиющей лжи и (2) оставлять открытой дверь для последующего уточнения, расширения или других модификаций, когда ученик будет продвигаться дальше. Проблема с историей MIRA в том, что, как показывают исследования, многие студенты остались с твердым, но ложным убеждением, что умножение на самом деле является повторяющимся сложением. Зная это, мы должны перестать рассказывать эту конкретную историю. Вторая часть моего ответа заключается в том, что в современном мире мы сталкиваемся с огромным количеством решений, которые зависят от понимания количества. Некоторые из них по своей природе аддитивны, некоторые мультипликативны, а некоторые экспоненциальны. Поведение этих трех разных видов арифметических операций резко различается, и, скажем, аддитивное мышление, когда задача является мультипликативной (или, что еще хуже, экспоненциальной), может привести к некоторым неверным решениям, которые во многих случаях действительно опасны.
Приведу всего два примера: плохое численное представление о риске может привести к ненужным расходам на безопасность авиакомпаний, как я указал в колонке за последний месяц, а отсутствие понимания экспоненциального роста может ослепить умных людей от катастрофических опасностей глобального потепления. . (Здесь я подчеркиваю математическую мысль; здесь задействовано много других факторов.) Это факт жизни, что многие люди проживут жизнь, не умея заниматься математикой. Когда им понадобятся услуги математически способного человека, они наверняка найдут кого-нибудь. Но в мире, построенном не только на словах и языке, но и на числах и арифметике, наши ученики достигают совершеннолетия без понимания четырех основных арифметических операций , ради всего святого, мне кажется, что это ситуация, с которой тем из нас, кто занимается математическим образованием, не следует мириться.
Хотя первоначальный фурор, вызванный моими первоначальными публикациями, кажется, улегся, я все еще получаю электронные письма от учителей и родителей типа «Хорошо, я понимаю, что вы говорите, но не могли бы вы тогда точно сказать мне, что такое умножение?» и от учителей, которые просят меня подсказать, как им учить маленьких детей умножению.
Эта колонка является ответом на эти запросы.
В общем и целом, мои ответы тем учителям, которые писали мне, исходили из той точки зрения, которую я избрал, когда писал первые три колонки. Я профессиональный математик, но не обученный учитель K-12. Мой опыт (и мои полномочия) связаны с математикой, а не с преподаванием. Как профессиональный математик, я могу (и считаю, что должен) давать советы по математике, которую преподают в школах, и конструктивно критиковать то, как ее преподают, но я не думаю, что мне уместно предлагать, как преподавать. Другие гораздо более опытны в этом, чем я. (Я думаю, что не случайно большинство профессоров математического образования — бывшие учителя. Трудно научить других делать то, чего не сделал сам.)
Обычно я отсылал своих корреспондентов к двум книгам, которые сам находил очень полезными для ознакомления с вопросами математического образования. Один Adding It Up: Helping Children Learn Mathematics, автором которой является Комитет по изучению обучения математике Национального исследовательского совета и опубликовано издательством National Academies Press в 2001 году.
Другая книга — это превосходная книга Терезины Нуньес и Питера Брайанта, изданная в 1996 году. Дети занимаются математикой. Есть и другие книги, и множество опубликованных научных статей по этому вопросу. Например, в 1994, Гершон Харел и Джере Конфри отредактировали гигантский том (414 страниц) под названием «Развитие мультипликативного мышления в изучении математики», который содержит множество результатов исследований, идей и полезных советов. (Все три книги доступны на Google книги.)
Проблема с моим ответом в том, что у учителей редко есть время, чтобы продираться через том в несколько сотен страниц, написанный в первую очередь для профессоров. Я знал это, но это были лучшие источники, с которыми я был знаком.
Что я могу (и сделаю) здесь, так это попытаюсь объяснить свое собственное понимание умножения. В некоторых случаях я подозреваю, что именно об этом просили мои корреспонденты. Но в своих ответах я лишь сделал несколько расплывчатых замечаний о том, что «это гораздо больше основано на реальной концепции масштабирования, чем на сложении».
Я не хотел идти дальше, потому что никто из нас на самом деле не знает, как мы сами изучаем или понимаем математику, не говоря уже о том, как это делают другие или могут найти в этом выгоду. Как профессиональный математик с многолетним стажем, мое понимание умножения может отличаться от понимания других, и, кроме того, некоторые его аспекты может быть трудно или невозможно передать ребенку, изучающему математику в первый раз. Никогда не преподавал на уровнях K-12, я бы не знал. Дело в том, что умножение и мультипликативные рассуждения сложны и многогранны. (Вот почему книга Харела-Конфри, которую я цитировал выше, занимает 414 страниц.)
Интересно, что сложности умножения почти никогда не возникают в повседневной деятельности профессионального математика. В самом деле, математик, который не задумывался о том, как этот предмет может — или должен — преподаваться на школьном уровне, может не знать об этих сложностях, хотя и сможет оценить их сразу же, как только на них укажут.
(Это, безусловно, было моей ситуацией на протяжении большей части моей карьеры.) Для математика умножение — это абстрактная бинарная функция чисел (и других абстрактных объектов), поведение которой определяется аксиомами. Мы никогда не задаемся вопросом «Что это?» мы также не пытаемся определить его в терминах «более основных» функций. (Замечу попутно, что на уровне формальной, аксиоматической математики умножение просто нельзя определить как повторяющееся сложение, поскольку последнее не является четко определенной функцией, а представляет собой метасхему вне аксиоматических рамок.) Мы просто используем функцию так, как это определено аксиомами.
Моя концепция умножения
Концепция умножения, которую я использую, когда работаю в математике, является скорее операциональной, чем онтологической, и построена на аксиоматически определенной абстрактной бинарной функции, которая составляет одну из двух фундаментальных операций в поле (или, в более общем смысле, в кольце).
Я знаю свойства умножения, как обязательные (например, ассоциативность), так и условные (например, коммутативность), как оно соотносится с другими функциями (например, дистрибутивность) и имеет ли конкретный пример обратную сторону. Мне удобно с этим справляться. Я не спрашиваю, что это такое; все, что имеет значение, это его свойства.Я понимаю, что моя профессиональная концепция умножения абстрагирована от повседневного понятия умножения, которое я выучил в детстве и использую в своей повседневной жизни. Но мое абстрактное представление об умножении упускает из виду многие сложности, которые являются частью моей гораздо более сложной ментальной концепции умножения как познавательного процесса. В этом вся суть абстракции. Хотя многие нематематики отступают от математического уровня абстракции, на самом деле это очень упрощает дело. Математика — это максимальное упрощение.
Например, математическая концепция умножения целых или действительных чисел коммутативна: M x N = N x M.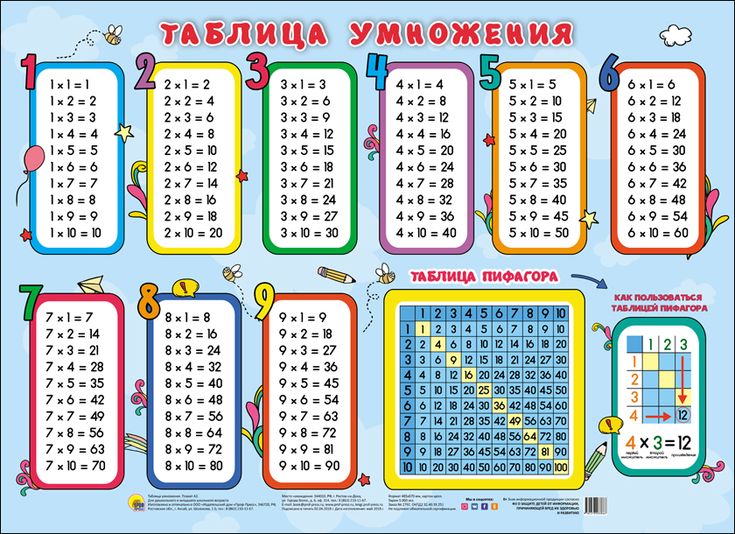
(Это одна из аксиом.) Порядок чисел не имеет значения. Здесь нет никаких единиц измерения: M и N — это чистые числа. Но неабстрактная, реальная операция умножения совершенно определенно не является коммутативной, и единицы измерения представляют собой серьезную проблему. Три мешка с четырьмя яблоками — это не то же самое, что четыре мешка с тремя яблоками. И взять эластичную ленту длиной 7,5 дюймов и растянуть ее в 3,8 раза — это не то же самое, что взять резинку длиной 3,8 дюйма и растянуть ее в 7,5 раза.
На самом деле природа единиц является основным различием между сложением и умножением, а также одной из нескольких причин, почему не стоит предполагать, что умножение является повторным сложением, даже в одном случае, когда повторное сложение имеет смысл, а именно, когда вы имеете дело с мощностями коллекций. Кроме того, две добавляемые коллекции должны иметь одинаковые единицы . Вы можете добавить 3 яблока к 5 яблокам, чтобы получить 8 яблок, но вы не можете добавить 3 яблока к 5 апельсинам.
Чтобы сложить, вам нужно изменить единицы измерения, чтобы сделать их одинаковыми, скажем, классифицируя их как фрукты, чтобы 3 фрукта плюс 5 фруктов равнялись 8 фруктам. Но для умножения два набора имеют совершенно разную природу и обязательно имеют разные единицы измерения . С умножением у вас есть множимое (записывается вторым), умноженное на множитель (записывается первым). Единицей для множителя должны быть наборы единиц для множимого. Например, если у вас есть 3 мешка, в каждом из которых по 5 яблок, то вы можете умножить их, чтобы получить
[3 ПАКЕТА] x [5 ЯБЛОК В ПАКЕТЕ] = 15 ЯБЛОКОВОбратите внимание, как единицы измерения сокращаются: МЕШКИ X ЯБЛОКИ/МЕШОК = 9 ЯБЛОК.0010 В этом примере есть возможность выполнения повторного сложения: вы заглядываете в каждый мешочек по очереди и складываете. В качестве альтернативы вы опорожняете 3 мешка и подсчитываете количество яблок. В любом случае вы определите, что яблок 15.
Конечно, вы получите тот же ответ, если умножите. Дело в том, что целочисленное умножение дает тот же ответ, что и многократное сложение. Но один и тот же ответ не делает операции одинаковыми.Заблуждение MIRA становится очень очевидным, когда вы рассматриваете мой второй пример, где я беру эластичную ленту длиной 7,5 дюймов и растягиваю ее в 3,8 раза. Окончательная длина ремешка составляет 28,5 дюймов. Но что такое единицы? Что идет после числа 3,8 в расчете
[3,8 — — -] x [7,5 ДЮЙМА] = 28,5 ДЮЙМА ?Ответ — ничего. У него нет единиц. В этом случае 3,8 является безразмерным масштабным коэффициентом .
Между прочим, даже когда начальная длина полосы и коэффициент масштабирования являются положительными целыми числами, нет смысла рассматривать этот пример как пример многократного сложения. Если я возьму резинку длиной 7 дюймов и растяну ее в 3 раза, ее окончательная длина составит
[3] x [7 ДЮЙМОВ] = 21 ДЮЙМНо я не брал 3 копии 7-дюймового ремешка и не соединял их вместе (дополнение), а масштабировал (растягивал) 7-дюймовый ремешок в 3 раза.
А как насчет использования умножения для вычисления площади прямоугольника? Если прямоугольник равен пи дюймов на е дюймов (где е — основание натуральных логарифмов), то его площадь равна
[ пи дюймов] x [ е дюймов] = пи.э кв. дюймов.или, в приблизительном числовом выражении, 3,14 дюйма x 2,72 дюйма = 8,54 кв. дюйма. Опять же, обратите внимание на единицы. (Обратите внимание, что повторное сложение в этом примере далеко не уйдет.)
Существуют и другие приложения умножения, в которых множитель и множимое имеют разные интерпретации предметной области, но, поскольку я не хочу писать колонку на 414 страниц, я оставлю это в надежде, что вы поймете мою точку зрения.
Итак, какова моя ментальная концепция умножения? Это целостная смесь всего вышеперечисленного и нескольких вариантов, которые я не перечислил. Вот почему я говорю, что умножение сложно и многогранно.
Доминирующий ментальный образ, который у меня есть, совершенно определенно является непрерывным масштабированием, и я вижу все остальные с точки зрения этого. Это означает, что моя концепция масштабирования в этом контексте является очень общей и охватывает такие примеры, как мои мешки с яблоками. Я могу рассматривать вычисление «3 мешка, в каждом из которых 5 яблок, всего 15 яблок» как «масштабирование» мешка с 5 яблоками в 3 раза. По моему опыту, овладение концепцией умножения равносильно созданию этой умственной амальгамы — амальгамы. это моя концепция умножения.
Я не знаю, как и когда я усвоил эту ориентированную на масштабирование концепцию умножения, и не могу передать ее словами (если только я просто не перечислил все ее многочисленные грани), но она была у меня, сколько я себя помню, и она определенно является единым, целостным понятием. Для меня эта концепция — то же самое, что умножение на . Таким образом, это числовая операция, которая соответствует очень общей форме масштабирования.
Меня этому научили, или я просто развил его со временем? Я не знаю. Есть ли у других математиков такая же концепция? Вероятно, хотя, как я отмечал ранее, онтологическая природа умножения редко возникает в профессиональной математической деятельности, поэтому, вероятно, очень немногие удосужились поразмыслить над этим вопросом.
С другой стороны, масштабирование — это естественное физическое понятие, и абстрагирование от физического масштабирования к числовой операции умножения не сложнее, чем абстрагирование от физического действия по объединению двух длин вместе для получения числовой операции сложения. Преимущество подхода к умножению на основе масштабирования состоит в том, что результирующая числовая операция работает во всех случаях, тогда как подход MIRA работает только для положительных целых чисел. (Конечно, вы можете рассказывать истории, чтобы распространить полученное понятие RA на рациональные числа, но оно надумано, и окончательный переход к действительным числам проблематичен.
Подход с масштабированием приводит вас к действительным числам за один раз, где действительные числа отождествляются с длинами. строк.)
Итак, для всех тех, кто спрашивал меня, это то, что I понимают под умножением: несколько обобщенное понятие масштабирования , построенное непосредственно на физической интуиции. И хотя, как я постоянно подчеркиваю, у меня нет опыта преподавания элементарной математики, я не могу понять, почему умножение не преподается таким образом.
Возможно, одна из причин того, что некоторые из нас более успешны в математике, чем другие, заключается в том, что нам удается формировать хорошие мыслительные концепции на ранних этапах процесса обучения. (Я не решаюсь использовать фразу «правильные понятия», так как я не знаю, что существует единственное правильное понятие умножения, и прекрасно осознаю, что мне трудно сформулировать свои слова словами.)
Угол Девлина обновлен в начале каждого месяца.
Найти больше столбцов здесь. Подпишитесь на Кита Девлина в Твиттере в @nprmathguy.Математик Кит Девлин (email: [электронная почта защищена]) Исполнительный директор Отдела гуманитарных наук Институт перспективных исследований и технологий (H-STAR) в Стэнфордском университете и Математик в выпуске выходного дня NPR. Его последний книга для широкого круга читателей Незаконченная игра: Паскаль, Ферма и Письмо семнадцатого века, сотворившее мир Современный, изданный Basic Books.
Что такое умножение? — Урок для детей
Математические курсы / Математика для детей Курс / Основы математики для начальной школы Глава
Инструктор: Дина Альберт
В этом уроке мы раскроем ~’магию~’ умножения и применим то, что мы знаем о сложении, к умножению. Мы рассмотрим случаи в реальной жизни, когда умножение пригодится!
Математик-Маг!
Прежде чем фокусник сможет выполнять фокусы, он должен изучить шаги и инструменты, чтобы фокус сработал.
То же самое и с «Математиком-Магом»! Умножение — это трюк, который мы изучаем сегодня. Мы будем использовать сложение в наших шагах и использовать некоторые изображения в качестве наших инструментов. Станем Математиками-Волшебниками!
Шаги: Сложение
Знали вы об этом или нет, иногда вы уже делаете умножение, просто складывая!
Умножение равно , сложив равных групп.
Пример 1:
Взгляните на эти три группы файлов cookie:
Поскольку в каждой группе 5 файлов cookie, они составляют равных групп.
Мы могли бы посчитать каждое печенье по одному, но мы также можем сложить по 5.
5 + 5 + 5 = всего 15 печений на картинке
Пример 2:
У вас есть три друга, и каждый из них хочет два яблока. Вам нужно знать, сколько всего яблок купить. Мы можем найти ответ на этот вопрос, взглянув на изображение яблок.
Мы можем добавить 2, чтобы найти общее количество яблок.
2 + 2 + 2 = всего 6 яблок. Итак, вам нужно купить 6 яблок.
Пример 3: Покупка наборов маркеров
На рисунке в каждой упаковке 6 маркеров. Вы покупаете 4 упаковки. Давайте добавим 6, чтобы вычислить, сколько всего маркеров у вас будет.
6 + 6 + 6 + 6 = всего 24 маркера
Время математической магии! Стать математическим волшебником.
Умножение — это другой способ записи количества групп на картинке и количества элементов в каждой группе.
Давайте еще раз посмотрим на картинку с яблоками:
Раньше мы писали 2 + 2 + 2
. Чтобы переписать это в терминах умножения:
1. Запишите, сколько существует равных групп.
2. Запишите количество предметов в каждой группе.
3. Поместите символ X между двумя числами. Это представляет собой умножение.
В примере с яблоком 3 (группы) X 2 (элементы в каждой группе).
Когда мы умножаем 3 x 2, мы складываем 3 группы по 2 яблока вместе. На картинке всего 6 яблок. Итак, 3 x 2 = 2 + 2 + 2 = всего 6 яблок
Давайте рассмотрим новый пример: Покупка газировки
Сначала посчитаем количество равных групп. В этом случае есть 2 равные группы.
Далее мы посчитаем количество бутылок содовой в одной группе. Есть 4 бутылки газировки.
Наконец, между двумя числами поставим знак умножения: 2 x 4
Итак, имеем:
2 (группы) x 4 (бутылки в каждой группе)
= 4 (бутылки в группе 1) + 4 (бутылки в группе 2) = всего 8 бутылок газировки.
2 x 4 = 8
За кулисами умножения
Теперь, когда у нас есть несколько примеров, давайте попробуем начать с умножения и переписать его в сложение.
3 x 4 = 12 файлов cookie
3 (группы) x 4 (файлы cookie в каждой группе) = всего 12 файлов cookie
4 (в группе 1) + 4 (в группе 2) + 4 (в группе 3) = 4 + 4 + 4 = 12
Другой пример: 4 x 5 = 20
4 группы по 5 яблок в каждой группе
= 5 яблок + 5 яблок + 5 яблок + 5 яблок
= всего 20 яблок, поэтому 4 x 5 = 20
Резюме урока
- Умножение — это более быстрый способ прибавления равного группы.
