Умножение дробей объяснение 5 класс: Умножение обыкновенных дробей — урок. Математика, 5 класс.

Конспект открытого урока по математике в 5 классе. Тема: Умножение обыкновенных дробей. | План-конспект урока по математике (5 класс):

Конспект открытого урока по математике в 5 классе.

Учитель Малиева В.В.

Тема урока: Умножение обыкновенных дробей.

Тип урока: Урок открытия нового знания. 

Цели:

Деятельностная цель: формирование у учащихся способностей к самостоятельному построению новых способов действия на основе метода рефлексивной самоорганизации.

Образовательная цель: расширение понятийной базы по теме «Действия с обыкновенными дробями»:

 вывести правило умножения дробей, сформировать умение умножать обыкновенные дроби. 

 В ходе урока учащиеся смогут:
-применить правило при решении упражнений.

Планируемые результаты:

Личностные результаты: формировать устойчивый познавательный интерес, умение работать в парах.

Метапредметные результаты.

Коммуникативные УУД: ученик получит возможность вступать в обсуждение, аргументируя свою точку зрения, используя адекватные языковые средства для отображения своих чувств, мыслей, мотивов и потребностей; развивать умение договариваться и приходить к общему решению в совместной деятельности на основе взаимоуважения к партнёру по работе.

Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.

Познавательные: записывать выводы в виде правил «если…, то…».

Предметные результаты:

• Формулировать правило умножения обыкновенных дробей.
• Применять правило умножения обыкновенных дробей при решении заданий.

Учебное оборудование: мультимедийный проектор, компьютер, экран, раздаточный материал. 

Ресурсы:

1. Алгоритм умножения обыкновенных дробей.
2. Задание на карточках.

3.Презентация «Умножение обыкновенных робей».

Этап (учебная ситуация)	Деятельность учителя	Деятельность учащихся
1.Этап мотивации.  Цель этапа: включение учащихся в деятельность на личностно-значимом уровне	— Здравствуйте! Садитесь. Проверьте все ли у вас готово к уроку. Запишите число.  Сегодня у нас не совсем обычный урок. Пожелайте удачи друг другу. Хочу начать урок со слов: «Дорогу осилит — идущий, математику – мыслящий!». А это значит, что мы на уроке будем думать и продолжим путь изучения математики.	Демонстрируют готовность к уроку
2. Актуализация знаний Цель этапа: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося	Устная работа. -Как называется число, записанное на доске? Что вы о нем знаете?  -Какая часть фигуры закрашена? -Как называются данные числа? 2/3, 4/9, 11/8, 12/5. -Как называются первые две дроби? Какие дроби называются правильными?  Другие две дроби. Какие две дроби называются неправильными? -Сократить дроби: (Что означает «Сократить дробь»? А каким свойством мы пользуемся при сокращении дробей?) 14/21, 10/30, 18/36, 5/10. -Сравнить дроби: (Повторяем правила сравнения дробей – комментарии) ½ и ¼, 5/7 и 5/9, 7/8 и 5/8, 11/15 и 4/15. (рассмотреть другие случаи) -Вычислить (решаем с комментариями) 1/6+ 2/6, 2/5 +5/6, 3/11-5/22, 6/18 — 4/18 1/3*5/6 — Сможем ли мы найти значение этого выражения?	Дают ответы: -Обыкновенные дроби. -Правильные дроби. Это дроби, у которых числитель меньше знаменателя. -Неправильные дроби. Это дроби, у которых числитель больше или равен знаменателю. -Если числители одинаковые, то больше та дробь, знаменатель которой меньше. -Если знаменатели одинаковые, то больше та дробь, знаменатель которой больше. -Выполняют сложение, вычитание Умножение 1/3*5/6. — Не умеем умножать дроби. Возможен ответ « да », гипотезу записать на доске, проверить решение в конце урока
3. Постановка проблемы.  Цель этапа: сформулировать проблему, тему и цели урока.	-Почему не смогли решить задачу? -Почему не смогли выполнить умножение дробей? -Как вы думаете, какая тема урока сегодня будет? -Запишите тему урока. -Какие цели поставим на сегодняшний урок? Чему вы хотели бы сегодня научиться?	— Не умеем умножать обыкновенные дроби. Умножение обыкновенных дробей. вывести правило умножения обыкновенных дробей -применять это правило при выполнении примеров и решении задач Записывают тему урока в тетради.
4. Открытие учениками нового знания. Цель этапа: организовать решение проблемной ситуации. Физминутка Цель этапа: снять напряжение у учащихся путем переключения на другой вид деятельности.	-Чтобы вывести правило умножения дробей, вспомним, как найти площадь прямоугольника. S= 4см*5см =20 см2. -Рассмотрим квадрат. Разделим его на равные квадраты. Сколько всего квадратов получилось?  Какая часть квадрата закрашена? Какая фигура получилась? (прямоугольник). Значит, площадь этого прямоугольника равна 12/25.   Длина этого квадрата равна 1, ее разделили на 5 частей и закрасили 4 части. Значит, длина прямоугольника составляет 4/5 от длины квадрата. А какую часть от ширины квадрата составляет ширина прямоугольника? (3/5) А как найти площадь этого прямоугольника? S=3/5*4/5, но мы получили, что площадь равна12/25. Значит, 3/5*4/5=12/25. (Мы умножаем две дроби. Как в числителе получить 12? Как в знаменателе получить 25? Давайте попробуем сформулировать правило умножения дробей: чтобы умножить две дроби, надо_____________________. Прочитать правило в учебнике вслух. Ещё раз расскажите правило своему соседу. —    Физминутка А теперь представим, детки, Будто руки наши – ветки. Покачаем ими дружно,  Словно ветер дует южный. Ветер стих. Вздохнули дружно. Нам урок продолжить нужно. Подравнялись, тихо сели И на доску посмотрели.	Выполняют задания. Озвучивают выводы. Читают правило в учебнике. Записывают формулу в тетради.
5. Этап закрепления изученного материала. Первичное закрепление Цель этапа: организовать решение и объяснение задания.	А сейчас мы будем работать по правилу. Решим №889. (Решение с комментариями детей.)	Учащиеся решают задания у доски с комментарием. Дети проговаривают правило (несколько человек).
6. Найдите ошибку в решении. Цель этапа: создать условия для закрепления правила умножения дробей Самостоятельная работа с самопроверкой Цель этапа: создать условия для самостоятельного решения и нахождения ошибок в работе.	1. Найдите ошибку в решении  *  =    *  =  = Самостоятельная работа с самопроверкой 2. Используя правило, выполните умножение обыкновенных дробей. 3/4 *5/7        1/2 *5/9 2/5*7/11         4/7 *5/11 1/8*3/4          2/5 *3/5 Выставите себе оценку за самостоятельную работу.	Выполняют самостоятельную работу с самопроверкой.
7.Этап контроля и оценки. Итог урока (рефлексия деятельности) Цель этапа: осознание уч-ся своей учебной деятельности, самооценка результатов деятельности своей и всего класса	-Какая задача стояла перед нами в начале урока? (Научиться умножать дроби.) Научились умножать дроби?   Тогда, оцените свою работу на уроке, зажгите светофор. Зажгите светофор          Зелёный цвет: Я хорошо потрудился на уроке.  Мне было интересно. Я доволен своей работой.   Желтый цвет: У меня возникали трудности на уроке, но я c ними справился. Я понял свои ошибки, и больше постараюсь не допускать их. Красный цвет: На уроке мне было  неинтересно. У меня было   много    ошибок. Я считаю, что мне еще нужно поработать над этой темой. Выставление оценок.	Дают ответы на вопросы. Анализируют работу на уроке через самооценку
Домашнее задание	1.Выучить правило умножения обыкновенных дробей. 2. Прочитать § 4.9 стр. 196   № 885на № 881 на Придумать задачу с практическим содержанием на тему: «Умножение обыкновенных дробей». Запасное задание. Математический диктант с устной проверкой 1.Запишите алгоритм умножения обыкновенных дробей. Чтобы умножить обыкновенные дроби надо: 1. Числитель первой дроби умножить на ____________________ , 2. _____________________ умножить на знаменатель второй, 3. ¾*1/5	Записывают домашнее задание

Карточка «математический диктант».

Запишите алгоритм умножения обыкновенных дробей.

Чтобы умножить обыкновенные дроби надо:

1. Числитель первой дроби умножить на __________________________________________________,

2. ____________________________________умножить на знаменатель второй дроби.

3.     *  =

Карточка «самостоятельная работа».

     а)  *                              г )   * 

     б)  *                            д)    *

     в)  *                             е)    *

Карточка «самостоятельная работа».

     а)  *                              г )   * 

     б)  *                            д)    *

     в)  *                             е)    *

Карточка «самостоятельная работа».

     а)  *                              г )   * 

     б)  *                            д)    *

     в)  *                             е)    *

примеры с дробями для тренировок

Тренажёр для 5 класса: примеры с дробями для тренировок

1 2 3 4 5 6 7 8 9 0 . C

Ответить

<table> <tr> <td> <p>3</p> <p>2</p> </td> <td> + </td> <td> <p>1</p> <p>2</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>1</p> <p>2</p> </td> <td> + </td> <td> <p>10</p> <p>3</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>1</p> <p>2</p> </td> <td> + </td> <td> <p>1</p> <p>6</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>7</p> <p>5</p> </td> <td> + </td> <td> <p>2</p> <p>8</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>6</p> <p>1</p> </td> <td> + </td> <td> <p>7</p> <p>4</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>1</p> <p>4</p> </td> <td> + </td> <td> <p>7</p> <p>4</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>1</p> <p>4</p> </td> <td> + </td> <td> <p>8</p> <p>4</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>5</p> <p>1</p> </td> <td> + </td> <td> <p>9</p> <p>8</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>7</p> <p>2</p> </td> <td> + </td> <td> <p>5</p> <p>2</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>4</p> <p>5</p> </td> <td> + </td> <td> <p>8</p> <p>7</p> </td> <td> = </td> </tr> </table>

Попробуй другие онлайн тренажеры с дробями

Сложение и вычитание дробей 5 класс

Обыкновенные дроби 5 класс примеры для тренировки

Умножение дробей.

Тренажер 5 класс

Что такое часть от целого?

Тема «дроби» в 5 классе в математике одна из самых сложных для восприятия школьниками. А упражнения с дробями в 5 класс вызывают страх и неприязнь. Без тренировки по этим темам никак!

Также эта тема очень большая, поскольку охватывает сразу несколько разделов. При изучении дробей в математике очень важно не упустить момент если ребенок что-то хоть немного недопонял или сомневается или не уверен.Главное сразу приступить к тренировкам и решению заданий и примеров на тему ДРОБИ для 5 класса. Чем раньше — тем лучше.

В данном случае главное объяснить где применяется «дробная часть числа», а также наглядность примеров дробей для 5 класса по математике. Само слово «Дробь» уже подразумевает дробление, деление, часть от чего-то. В школьной программе 5 класса к примерам по математике для тренировки с дробями приступают только после изучения всех операций над целыми числами. Вначале дети тренируются на примерах с простыми дробями для 5 класса по математике . Затем, приступают к примерам сложнее на умножение дробей. Их также легко можно отработать на тренажёре умножения дробей

Но объяснить ребенку что такое обыкновенные дроби и решать задания, и познакомиться с примерами решения дробей лучше гораздо раньше.

Это сформирует пространственное представление и логическое мышление. Наш тренажер сложения дробей в этом, конечно, поможет. А в 5 классе изучение дробей со сверстниками не составит труда! Но если надо решить уже имеющуюся дробь, ту придет на помощь калькулятор решающий дроби. Вы также можете распечатать примеры на дроби для 5 класса с ответами для тренировки
Как бы ребенок не решал упражнения с дробями для 5 класса для тренировки подойдет любой способ. Хоть решать решать обыкновенные дроби используя онлайн тренажер, хоть распечатать и решать на листке бумаги примеры с простыми дробями для 5 класса для тренировки на нашем сайте. Главное много практики, много упражнений с дробями и много тренировок. В 5 классе главное отточить навыки.

Как рассказать про часть, чтобы ребенок понял?

Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы. Правильные дроби – это дроби, в которых числитель меньше знаменателя Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя

Дробь — число не целое, оно обозначает количество долей целого

Обыкновенная дробь состоит из двух частей: числитель и знаменатель

Дроби бывают правильные и неправильные. У правильных дробей числитель меньше знаменателя.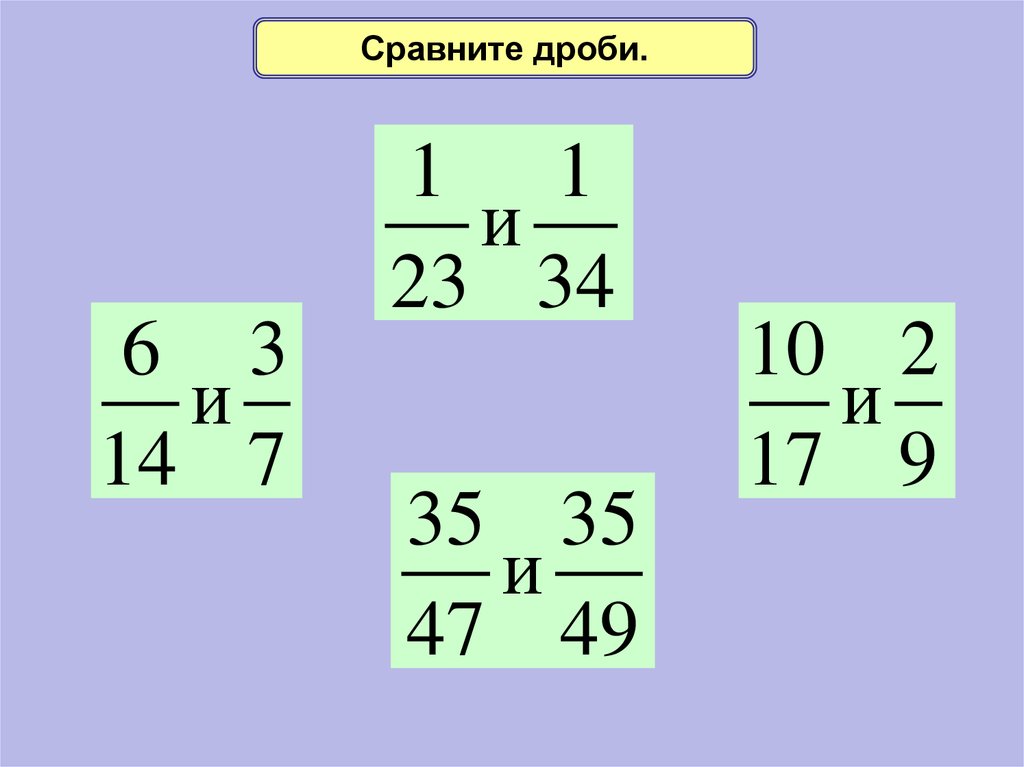 У неправильных дробей наоборот, числитель больше знаменателя, а значит любую неправильную дробь можно перевести в смешанную, выделив у нее целую часть и отняв ее из числителя

Познакомься с другими тренажерами курса

Меры измерения

Мер величин много и в них легко запутаться. Изучайте меры длины, времени и массы на тренажере

Скорей заниматься

Римские цифры

Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры

Скорей заниматься

Задачи на объем, площадь, периметр

Решение задач на применение формул объем, площадь, периметр

Скорей заниматься

Умножение дробей — Элементарная математика

Введение

Общие основные стандарты

Как умножать дроби

Советы по умножению дробей

Наши любимые ошибки

Вопросы на умножение дробей

Часто задаваемые вопросы об умножении дробей

Следующие уроки

Все еще застряли?

[БЕСПЛАТНО] Математические экзамены на конец года (4-й и 5-й классы)

Экзамены охватывают ряд тем, чтобы оценить успеваемость ваших учеников по математике и помочь подготовить их к экзаменам штата.

Скачать бесплатно

Введение

Общие основные стандарты

Как умножать дроби

Советы по умножению дробей

Наши любимые ошибки

Практикуйте умножение дробей вопросы

Часто задаваемые вопросы об умножении дробей

Следующие уроки

Все еще застряли?

Здесь вы узнаете о умножении дробей в том числе о том, как умножать дроби вместе, умножать дроби на целые числа и умножать смешанные числа.

Сначала учащиеся узнают об умножении единичных дробей и целых чисел в составе числа и действиях с дробями в 4-м классе. Они будут опираться на это понимание и умножать дроби на дроби в составе числа и действия в дробях в 5 классе.

Что такое умножение дробей?

Умножение дробей — это умножение одного или нескольких чисел в виде дроби. Фракции можно умножать с помощью моделей или алгоритма.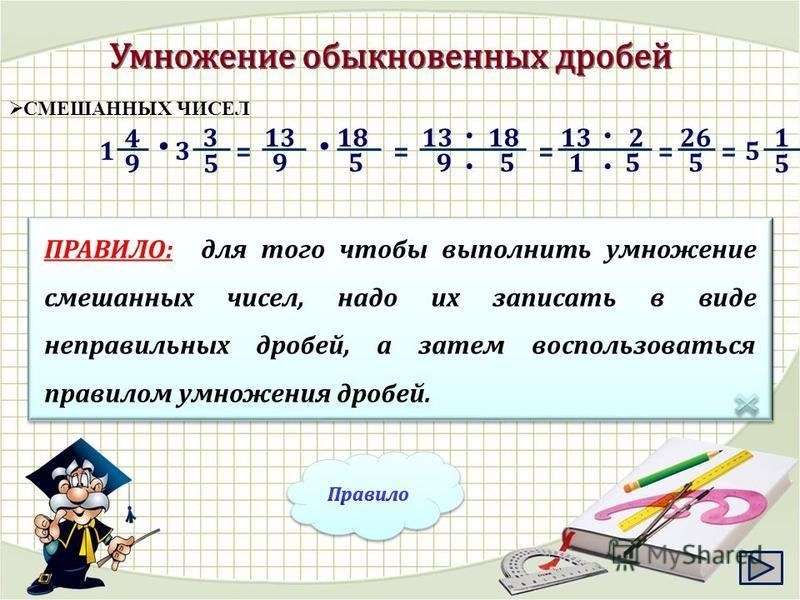

Например…

Умножение единичной дроби на целое число

4 \times \cfrac{1}{3}

Использование моделей:

Модель показывает \cfrac{1}{3} из 4, поэтому 4 \times \cfrac{1}{3} = \cfrac{4}{3}.

Вы также можете думать о 4 \times \cfrac{1}{3} как о 4 группах \cfrac{1}{3} или \cfrac{1}{3}+\cfrac{1}{3}+\ cfrac{1}{3}+\cfrac{1}{3}, то есть \cfrac{4}{3}.

Используя алгоритм:

Запишите 4 как неправильную дробь, 4=\cfrac{4}{1}, затем умножьте числители, затем знаменатели:

\cfrac{4}{1} \times \cfrac {1}{3}=\cfrac{4}{3}.

Умножение дроби на целое число

3 \times \cfrac{2}{5}

Использование моделей:

Модель показывает \cfrac{2}{5} из 3, поэтому 3 \times \cfrac{ 2}{5}=\cfrac{6}{5}.

Вы также можете представить 3 \times \cfrac{2}{5} как 3 группы \cfrac{2}{5} или \cfrac{2}{5}+\cfrac{2}{5}+\ cfrac{2}{5}, то есть \cfrac{6}{5}.

Используя алгоритм:

Запишите 3 как неправильную дробь, 3=\cfrac{3}{1}, затем умножьте числители, затем знаменатели:

\cfrac{3}{1} \times \cfrac {2}{5}=\cfrac{6}{5}.

Умножение дробей на дроби

\cfrac{1}{2} \times \cfrac{1}{3}

Использование моделей:

В модели \cfrac{1}{3} выделен желтым цветом, а \cfrac {1}{2} — синий.

Продукт, в котором дроби перекрываются зеленым цветом.

Модель показывает \cfrac{1}{3} из \cfrac{1}{2}, поэтому \cfrac{1}{2} \times \cfrac{1}{3}=\cfrac{1}{6 }.

Используя алгоритм:

Умножьте числители, затем знаменатели: \cfrac{1}{2} \times \cfrac{1}{3}=\cfrac{1}{6}.

Умножение смешанных чисел

1 \cfrac{2}{3} \times 2 \cfrac{1}{6}

Использование моделей:

В модели 1 \cfrac{2}{3} окрашен желтым цветом, а 2 \cfrac{1}{6} — синим.

Произведение находится там, где перекрываются смешанные числа.

Модель показывает 1 \cfrac{2}{3} группы по 2 \cfrac{1}{6}.

Обратите внимание, что у вас есть 2 целого, и перемещение \cfrac{1}{3} в \cfrac{2}{3} равно \cfrac{3}{3}, что дает еще одно целое.

Также есть \cfrac{1}{3}, \cfrac{1}{6} и \cfrac{2}{18}.

Чтобы найти произведение, нужно сложить эти дроби с тремя целыми.

\begin{align} & 3+\cfrac{1}{3}+\cfrac{1}{6}+\cfrac{2}{18} \\\\ & =3+\cfrac{1 \times 6} {3 \times 6}+\cfrac{1 \times 3}{6 \times 3}+\cfrac{2}{18} \\\\ & =3+\cfrac{6}{18}+\cfrac{ 3}{18}+\cfrac{2}{18} \\\\ & =3 \cfrac{11}{18} \end{выровнено}

Используя алгоритм:

Преобразуйте смешанные числа в неправильные дроби.

\hspace{1cm} 2 \cfrac{1}{6}=\cfrac{13}{6} \hspace{1cm} и \hspace{1cm} 1 \cfrac{2}{3}=\cfrac{5 }{3}

Умножьте числители, затем знаменатели: \cfrac{13}{6} \times \cfrac{5}{3}=\cfrac{65}{18}.

Запишите \cfrac{65}{18} как смешанное число: 3 \cfrac{11}{18}.

Что такое умножение дробей?

Общие базовые стандарты

Как это относится к математике в 4-м и 5-м классах?

• Класс 4 – Числа и операции – Дроби (4. NF.B.4b)
  Понимание кратного \cfrac{a}{b} как кратного \cfrac{1}{b} и использование это понимание умножения дроби на целое число.

• 5 класс – Числа и операции – Дроби (5.NF.B.4b)
  Применить и расширить прежнее понимание умножения, чтобы умножить дробь или целое число на дробь.

Как умножать дроби

Для умножения дробей с моделями:

1. Нарисуйте одну дробь по горизонтали, а другую по вертикали.
2. Соедините дроби \bf{2} разных цветов.
3. Подсчитайте перекрытия.
4. Если возможно, упростите или преобразуйте в смешанное число.

Для умножения дробей по алгоритму:

1. Перемножьте числители.
2. Перемножьте знаменатели.
3. Если возможно, упростите или преобразуйте в смешанное число.

Чтобы умножать целые числа или смешанные числа на дроби по алгоритму:

1. Преобразовать в неправильные дроби.
2. Перемножьте числители.
3. Перемножьте знаменатели.
4. Если возможно, упростите или преобразуйте в смешанное число.

[БЕСПЛАТНО] Проверка понимания дробей (для 4–6 классов)

Используйте этот тест, чтобы проверить понимание дробей учащимися 4–6 классов. Более 10 вопросов с ответами, охватывающими ряд тем 4-го, 5-го и 6-го классов, чтобы определить сильные стороны и поддержку!

СКАЧАТЬ БЕСПЛАТНО

Икс

[БЕСПЛАТНО] Тест «Проверка понимания дробей» (4–6 классы)

Используйте этот тест, чтобы проверить понимание дробей учащимися 4–6 классов. Более 10 вопросов с ответами, охватывающими ряд тем 4-го, 5-го и 6-го классов, чтобы определить сильные стороны и поддержку!

СКАЧАТЬ БЕСПЛАТНО

Примеры умножения дробей

Пример 1: умножение дроби на дробь с помощью модели

Решите \cfrac{2}{5} \times \cfrac{3}{8} с помощью модели.

1. Нарисуйте одну дробь по горизонтали, а другую по вертикали.  

Нарисуйте прямоугольник. Разделите одну сторону на пятые части.

Разделите другую сторону на восьмые.

2 Соедините дроби до конца с помощью \bf{2} разных цветов.

Закрасьте \cfrac{2}{5} желтым цветом и \cfrac{3}{8} синим цветом.

3 Подсчитайте перекрытие.

Продукт, в котором дроби перекрываются зеленым цветом.

Модель показывает \cfrac{3}{8} из \cfrac{2}{5}, поэтому \cfrac{2}{5} \times \cfrac{3}{8}=\cfrac{6}{40 }, потому что зеленых квадратов 6, а всего 40 квадратов.

4 Если возможно, упростите или преобразуйте в смешанное число.

Продукт может быть упрощен.

И 6, и 40 имеют коэффициент 2, поэтому их можно разделить на 2 : \cfrac{6 \; \дел\; 2}{40 \; \дел\; 2}=\cfrac{3}{20}.

Итак, \cfrac{2}{5} \times \cfrac{3}{8}=\cfrac{6}{40} \ или \, \cfrac{3}{20}.

Пример 2: умножение дроби на дробь с помощью модели

Решите \cfrac{3}{4} \times \cfrac{1}{6} с помощью модели.

Нарисуйте одну дробь по горизонтали, а другую по вертикали.

Нарисовать прямоугольник. Разделите одну сторону на четверти.

Разделите другую сторону на восьмые.

Соедините дроби \bf{2} разных цветов.

Закрасьте \cfrac{3}{4} желтым цветом и \cfrac{1}{6} синим цветом.

Подсчитайте перекрытие.

Продукт, в котором дроби перекрываются зеленым цветом.

Модель показывает \cfrac{1}{6} из \cfrac{3}{4}, поэтому \cfrac{3}{4} \times \cfrac{1}{6}=\cfrac{3}{ 24}, потому что зеленых квадратов 3, а всего 24 квадрата.

Если возможно, упростите или преобразуйте число в смешанное.

Продукт может быть упрощен.

И 3, и 24 имеют коэффициент 3, поэтому их можно разделить на 3 : \cfrac{3 \; \дел\; 3}{24\; \дел\; 3}=\cfrac{1}{8}.

Итак, \cfrac{3}{4} \times \cfrac{1}{6}=\cfrac{3}{24} \ или \, \cfrac{1}{8}.

Пример 3: умножение дроби на дробь по алгоритму

Решите \cfrac{5}{12} \times \cfrac{2}{3}.

Перемножьте числители.

\cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{}

Перемножьте знаменатели.

\cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{36}

Если возможно, упростите или преобразуйте в смешанное число.

Продукт может быть упрощен.

И 10, и 36 имеют коэффициент 2, поэтому их можно разделить на 2 : \cfrac{10 \; \дел\; 2}{36\; \дел\; 2}=\cfrac{5}{18}.

Итак, \cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{36} \ или \, \cfrac{5}{18}.

Пример 4: умножение дроби на дробь по алгоритму

Решите \cfrac{1}{2} \times \cfrac{7}{10}.

Перемножьте числители.

\cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{}

Перемножьте знаменатели.

\cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{20}

Если возможно, упростите или преобразуйте в смешанное число.

Продукт не может быть упрощен. 7 и 20 имеют только общий делитель 1.

Итак, \cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{20}.

Пример 5: умножение целого числа на дробь с помощью алгоритма

Решите \cfrac{2}{9} \times 4.

Преобразование в неправильные дроби.

Запишите 4 как неправильную дробь, 4=\cfrac{4}{1}.

Перемножьте числители.

\cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{}

Перемножьте знаменатели.

\cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{9}

Если возможно, упростите или преобразуйте в смешанное число.

Продукт не может быть упрощен. 8 и 9 имеют только общий делитель 1.

Итак, \cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{9}.

Пример 6: умножение смешанного числа на дробь по алгоритму

Решите \cfrac{3}{8} \times 3 \cfrac{5}{8}.

Преобразование в неправильные дроби.

Преобразуйте смешанное число в неправильную дробь.

3 \cfrac{5}{8}=\cfrac{29}{8}

Перемножьте числители.

\cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{}

Перемножьте знаменатели.

\cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{64}

Если возможно, упростите или преобразуйте в смешанное число.

Числитель больше знаменателя, поэтому неправильную дробь можно преобразовать в смешанное число.

\cfrac{87}{64}=1 \cfrac{23}{64}

Продукт не может быть упрощен. 23 и 64 имеют только общий делитель 1.

Итак, \cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{64} \, или \, 1 \ cfrac{23}{64}

Советы по умножению дробей

• Умножение дробей представляет собой сложную задачу для учащихся начальной школы. Этот тип умножения плохо сочетается с идеей многократного сложения, на которую учащиеся полагаются при умножении целых чисел. Максимально используйте практические визуальные модели и/или цифровые модели, чтобы учащиеся могли понять, что такое умножение дробей и почему алгоритм работает.

• Изучите шаблоны, чтобы учащиеся могли понять простые шаги, связанные с умножением дробей.

• Сами по себе рабочие листы не помогут глубоко понять эту тему. Включение визуальных моделей, практических занятий и цифровых игр — очень эффективная альтернатива простому использованию рабочих листов для умножения дробей.

Наши любимые ошибки

• Путаница в правилах умножения и деления
  При умножении нет необходимости переворачивать вторую дробь (использовать обратную), как при делении.
  Например,

• Умножение крестом
  Если учащиеся знакомятся с умножением крестом, они могут запутаться и использовать его при умножении двух дробей.
  Например,

• Нахождение общего знаменателя
  Нет необходимости находить общий знаменатель при умножении дробей, как при сложении или вычитании дробей. Хотя это не приведет к неправильному ответу, оно создаст ненужную работу и больше возможностей для ошибок.
  Например,
  Нет общего знаменателяОбщий знаменатель
  создано: создано:

Практикуйтесь в вопросах умножения дробей используя модель, нарисуйте прямоугольник. Разделите одну сторону на трети.

 

 

Разделите другую сторону на десятые.

 

 

Закрасьте \cfrac{1}{3} синим и \cfrac{9}{10} желтым.

 

 

Произведение, где дроби перекрываются зеленым цветом.

 

Модель показывает \cfrac{9}{10} из \cfrac{1}{3}, поэтому \cfrac{1}{3} \times \cfrac{9}{10}=\cfrac{9} {30}, потому что зеленых квадратов 9, а всего 30 квадратов.

 

Продукт может быть упрощен.

 

И 9, и 30 имеют коэффициент 3, поэтому их можно разделить на 3 : \cfrac{9\; \дел\; 3}{30\; \дел\; 3}=\cfrac{3}{10}.

 

Итак, \cfrac{1}{3} \times \cfrac{9}{10}=\cfrac{9}{30} \ или \, \cfrac{3}{10}.

\cfrac{20}{30}

\cfrac{25}{24}

\cfrac{9}{11}

\cfrac{49}{30}

Чтобы решить с помощью модели, начертите прямоугольник. Разделите одну сторону на шестые.

 

 

Разделите другую сторону на пятые.

 

 

Закрасьте \cfrac{5}{6} желтым цветом и \cfrac{4}{5} синим цветом.

 

 

Произведение показывает, где дроби перекрываются зеленым цветом.

 

Модель показывает \cfrac{4}{5} из \cfrac{5}{6}, поэтому \cfrac{5}{6} \times \cfrac{4}{5}=\cfrac{20} {30}, потому что зеленых квадратов 20, а всего 30 квадратов.

 

Продукт может быть упрощен.

 

И 20, и 30 имеют коэффициент 10, поэтому их можно разделить на 10 : \cfrac{20 \; \дел\; 10}{30\; \дел\; 10}=\cfrac{2}{3}.

 

Итак, \cfrac{5}{6} \times \cfrac{4}{5}=\cfrac{20}{30} \; или \; \cfrac{2}{3}.

\cfrac{110}{36}

\cfrac{55}{18}

\cfrac{14}{22}

\cfrac{33}{120}

Перемножьте числители: \cfrac{ 11}{12} \times \cfrac{3}{10}=\cfrac{33}{}.

 

Затем перемножьте знаменатели: \cfrac{11}{12} \times \cfrac{5}{10}=\cfrac{33}{120}.

 

Продукт не может быть упрощен. 33 и 120 имеют только общий делитель 1,

 

S0, \cfrac{11}{12} \times \cfrac{5}{10}=\cfrac{33}{120}.

\cfrac{2}{55}

\cfrac{10}{55}

\cfrac{10}{11}

\cfrac{57}{9}

Запишите 5 как неправильную дробь, 5 =\cfrac{5}{1}.

 

Затем перемножьте числители: \cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{}.

 

Затем перемножьте знаменатели: \cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{11}.

 

Продукт не может быть упрощен. 10 и 11 имеют только общий делитель 1.

 

Итак, \cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{11}.

4 \cfrac{2}{5}

3 \cfrac{2}{15}

2 \cfrac{17}{18}

2 \cfrac{13}{15}

Преобразование смешанных чисел к неправильным дробям.

 

\hspace{1cm} 3 \cfrac{2}{3}=\cfrac{11}{3} \hspace{1cm} и \hspace{1cm} 1 \cfrac{1}{5}=\cfrac {6}{5}

 

 

Затем умножьте числители вместе: \cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{}.

 

Затем перемножьте знаменатели: \cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{15}.

 

Числитель больше знаменателя, поэтому неправильную дробь можно преобразовать в смешанное число.

 

\cfrac{66}{15}=4 \cfrac{6}{15}

 

Продукт может быть упрощен.

 

И 6, и 15 имеют коэффициент 3, поэтому их можно разделить на 3 : \cfrac{6 \; \дел\; 3}{15\; \дел\; 3}=\cfrac{2}{5}.

 

Итак, \cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{15} \; или \; 4 \cfrac{2}{5}.

Площадь прямоугольника равна \text { основание } \times \text { высота }, поэтому для определения площади стены нам нужно вычислить 4 \cfrac{2}{5} \times 2 \cfrac{1} {4}.

 

Преобразуйте смешанные числа в неправильные дроби.

 

\hspace{1cm} 4 \cfrac{2}{5}=\cfrac{22}{5} \hspace{1cm} и \hspace{1cm} 2 \cfrac{1}{4}=\cfrac {9}{4}

 

 

Затем умножьте числители вместе: \cfrac{22}{5} \times \cfrac{9}{4}=\cfrac{198}{}.

 

Затем перемножьте знаменатели: \cfrac{22}{5} \times \cfrac{9}{4}=\cfrac{198}{20}.

 

Числитель больше знаменателя, поэтому неправильную дробь можно преобразовать в смешанное число. 92 стены.

Часто задаваемые вопросы об умножении дробей

Является ли умножение дробей тем же, что и делением дробей?

Нет, когда вы умножаете дроби, вы умножаете дроби вместе и не берете обратное значение второй дроби. Когда вы делите дроби, вы умножаете на обратную величину делителя.

Какой словарь используется для умножения дробей?

Важно знать следующие термины…
◌ Знаменатель: нижнее число
◌ Числитель: наибольшее число
◌ Произведение: ответ на уравнение умножения

Должен ли окончательный ответ быть в наименьшем выражении?

Хотя учащимся предлагается использовать наибольший общий делитель (НОД) для упрощения произведений до минимума, это не является обязательным условием для понимания ими этого навыка. Кроме того, в каждом штате разные ожидания относительно того, когда учащиеся должны использовать самые низкие термины. Обратитесь к государственным стандартам за разъяснениями.

Следующие уроки

• Деление дробей
• Преобразование дробей, десятичных знаков и процентов
• Передаточные числа

Все еще зависает?

Компания Third Space Learning специализируется на оказании помощи учителям и школьным руководителям в оказании персонализированной помощи по математике большему количеству учащихся посредством высококачественных индивидуальных онлайн-репетиторских занятий по математике, проводимых экспертами-предметниками.

Каждую неделю наши преподаватели поддерживают тысячи учеников, которые рискуют не оправдать свои ожидания в классе, и помогают ускорить их прогресс и повысить уверенность в себе.

Узнайте, как мы можем помочь вашим ученикам добиться успеха с помощью наших программ обучения математике для начальной школы.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в ​​отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Принять помогите своим ученикам достичь мастерства! Эти увлекательные занятия, представленные в нескольких формах обучения, позволят вашим учащимся эффективно умножать различные типы дробей. Будь то в цифровом виде, с вкусными закусками или с манипуляциями, эти различные типы ресурсов откроют множество путей обучения для ваших подающих надежды математиков, поскольку они будут практиковаться в умножении как правильных, так и неправильных дробей.

1. Умножение дробей Лабиринт из водосточных труб

Используйте этот креативный лабиринт из водосточных труб, чтобы научиться умножать дроби. Этот ресурс отлично подходит для обучения студентов навыкам самооценки, поскольку они должны перепроверять свою работу с предоставленными кусочками головоломки, когда они перемещаются по этому занимательному лабиринту дробей.

Дополнительные сведения: общий основной материал

2. Умножение дробей домино

Сыграйте в эту игру домино, состоящую из трех раундов, чтобы научить учащихся умножать дроби. Создайте коврик для умножения, изображенный ниже, и используйте домино для умножения числителей и знаменателей. Это идеальный ресурс для ротации математических центров.

Дополнительные сведения: Обучающие материалы

3. Умножение дробей на целое число

Расширьте знания учащихся о дробях с помощью этого практического материала. Используйте маркеры и бумагу для создания этих интерактивных карточек, которые позволят учащимся получить концептуальное представление об умножении дробей на целые числа.

Узнайте больше: K5 Math Spot

4. Умножайте и делите дроби с помощью закусок

Помогите пятиклассникам развить понимание дробей с помощью школьной забавы! В этом упражнении используются закуски и угощения для повторения словесных задач, связанных с умножением и делением дробей. Учащимся понравится манипулировать этими закусками, чтобы углубить свое понимание.

Узнайте больше: Дженнифер Финдли

5. Безумие умножения: настольная игра «Умножение дробей»

С помощью этой интерактивной настольной игры ваши ученики и дети будут в восторге от уроков дробей. В этой игре игроки будут пытаться гонять свои отдельные фигуры по доске, умножая дроби на целые числа.

Подробнее: Учителя платят учителям

6. Умножение дробей Цифровые или физические карточки с заданиями

Раздайте эти карточки с заданиями в цифровом виде, чтобы ваши ученики попрактиковались в умножении дробей. Эти карточки также можно распечатать и использовать в классе во многих различных играх. Карточки с физическими заданиями также можно использовать в охоте за мусором, игре на память или в качестве самостоятельной центральной работы.

Подробнее: Учителя платят учителям

7. Умножение дробей на дроби Игра Scoot

Используйте это увлекательное занятие в классе, чтобы научить своих учеников умножать дроби. Эта игра помогает включить некоторые движения в вращения математического центра. Просто разложите задачи по комнате и наблюдайте, как учащиеся путешествуют; пытаясь найти правильные ответы.

Дополнительная информация: Уголок учебной программы

8. Блоки шаблонов и умножение дробей

Умножайте дроби на дроби, используя эти блоки шаблонов. Это упражнение с дробями, предназначенное для учащихся 4-х и 5-х классов, позволяет учащимся использовать манипуляции для представления дробей, которые они будут умножать. Используйте те блоки шаблонов, которые у вас есть, чтобы представить дроби, и просто добавьте лист разлинованной бумаги в смесь, чтобы ваши ученики могли попрактиковаться в умножении.

Дополнительные сведения: Mix and Math

9. Практическая математика Умножение дробей

Попросите учащихся разыграть и смоделировать примеры сценариев, в которых им нужно будет умножать дроби в повседневной жизни! Они получат хорошее представление о том, что требуется для нескольких дробей, с помощью этих двух раздаточных материалов, дополненных рабочим листом для размышлений учащихся и ключом для ответов.

Дополнительная информация: Учителя платят учителям

10. Задания на дроби: умножение и деление

Решайте текстовые задачи, требующие от учащихся практики умножения и деления дробей. Эти текстовые задачи помогут учащимся увидеть реальную ценность умения умножать и делить дроби.

Подробнее: Дженнифер Финдли

11. Песня об умножении дробей и интерактивная викторина

Используйте эту забавную математическую анимацию в своем обучении, чтобы помочь учащимся понять, как умножать дроби на целые числа. Выйдите за рамки традиционных методов обучения, научив их этой песне, а затем протестируйте их с помощью цифрового инструмента викторины.

Подробнее: Number Rock

12. Математический вымпел Умножение дроби

Покажите работу вашего ученика с помощью этих вымпелов. Эти привлекательные вымпелы позволят учащимся продемонстрировать свою работу после решения сложной дроби. Эти простые бумажные фигуры украсят любой урок математики!

Узнать больше: Scaffolded Math

13. Умножение смешанных чисел Упражнение

Освойте умножение дробей с помощью этих забавных головоломок со смешанными числами. Учащимся понравятся эти головоломки, поскольку они представляют собой веселый и энергичный способ помочь им попрактиковаться в умножении дробей. Добавьте их к занятиям в математическом центре или включите их в игру, чтобы составить увлекательный план урока.

Подробнее: Math Geek Mama

14. Упражнение «Складывание бумаги»

Используйте это простое упражнение с бумагой, чтобы учащиеся попрактиковались в умножении дроби на дробь. Листы бумаги и письменные принадлежности — все, что нужно для создания этих простых в использовании руководств по умножению дробей.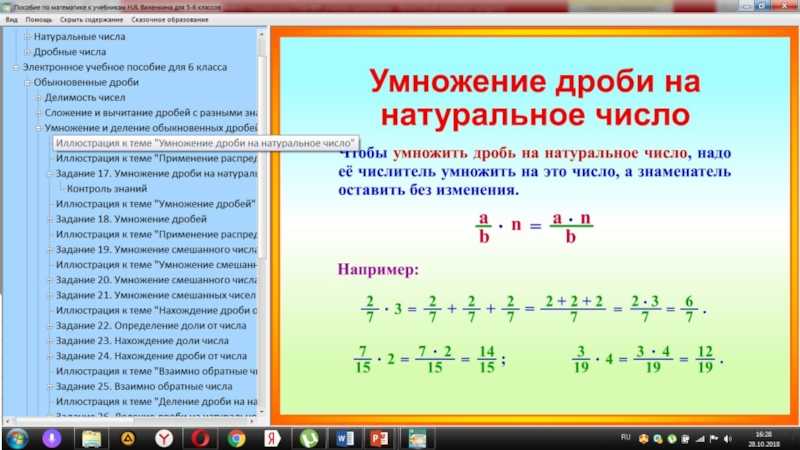

Дополнительная информация: Kaathadi

15. Умножение дробей с использованием моделей

Используйте эти модели умножения дробей, чтобы закрепить единицу дроби. Эти модели подходят для повторения до 8-го класса для практики умножения дробей на целые числа, другие дроби или смешанные числа.

Дополнительные сведения: Маневрирование в середине

16. Видео с практическими занятиями

Используйте бумагу, маркеры, ножницы и линейку для создания простых интерактивных манипуляторов, которые учащиеся могут использовать с умножением дробей. Они идеально подходят для модели перевернутого класса или математических центров и помогают сделать обучение легким и увлекательным!

Дополнительные сведения: Mashup Math

17. Цифровой ресурс по умножению дробей

Используйте цифровые ресурсы в единицах дробей, чтобы познакомить учащихся с еще одной идеей интерактивного обучения. Эти виртуальные манипуляторы облегчают учащимся создание моделей областей рисования! Назначьте доски, чтобы учащиеся практиковали свою работу после цифрового умножения дробей.

Узнайте больше: Живите Смейтесь Любите учиться

18. Умножение дробей на дроби и целые числа

Следуйте этим простым пошаговым инструкциям о том, как умножать дроби. Используйте анимационный видеоурок, бесплатный рабочий лист и предоставленный ключ к ответу, чтобы умножить дробь цемента в уме ваших учеников.

Дополнительные сведения: Mashup Math

19. Умножение дробей Опорная диаграмма

Воссоздайте эту опорную диаграмму, чтобы ваши ученики могли видеть ее во время выполнения своей работы. Будьте преднамеренными, создав это на диаграммной бумаге, чтобы учащиеся могли использовать ее в качестве модели.