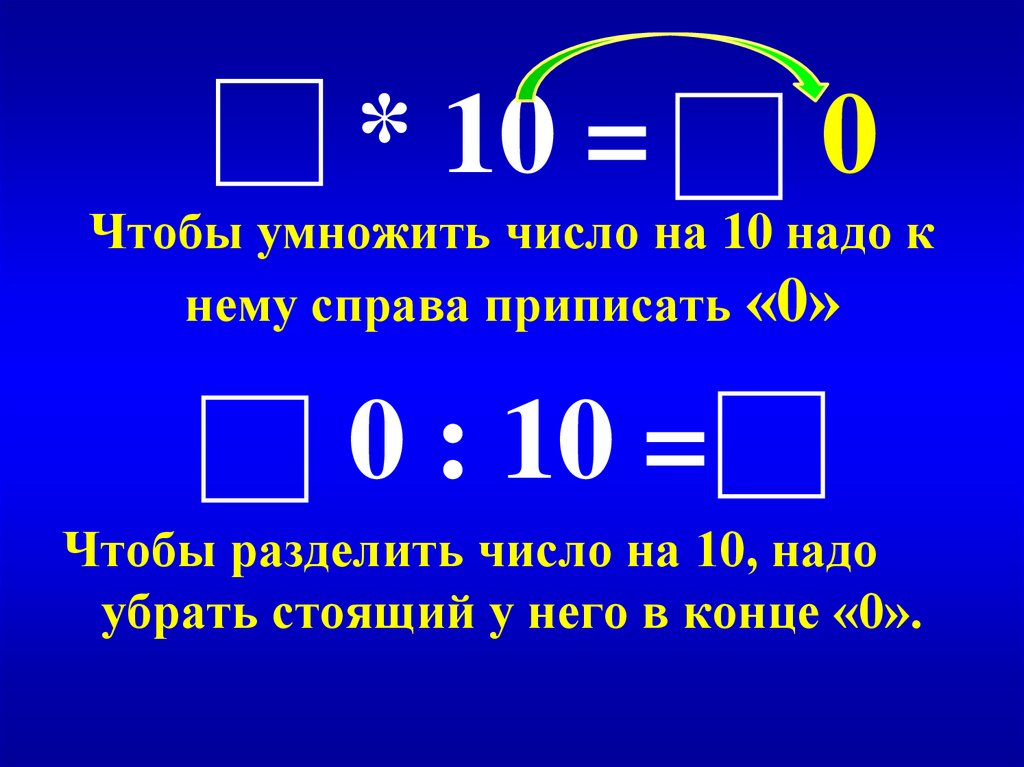
Умножение и деление целых чисел. Возведение в степень
- Умножение
- Деление
- Возведение в степень
Умножение
При умножении двух целых чисел умножаются их абсолютные величины. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные
Примеры:
3 · 5 = 15,
3 · (-5) = -15,
-3 · 5 = -15,
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | — | = | — |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное

При умножении любого числа на -1 получится число противоположное данному.
Примеры:
-15 · (-1) = 15,
25 · (-1) = -25.
Деление
При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3,
15 : (-5) = -3,
-15 : 5 = -3,
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число противоположное данному.
Примеры:
-15 : (-1) = 15,
25 : (-1) = -25.
Возведение в степень
При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.
Степень положительного числа всегда будет положительным числом.
Примеры:
52 = 5 · 5 = 25,
43 = 4 · 4 · 4 = 64.
Степень отрицательного числа может быть как положительным, так и отрицательным числом.
Примеры:
Нечётный показатель степени:
| (-3)3 = | (-3) · (-3) | · (-3) = |
| + |
= 9 · (-3) = -27,
то есть (-3)3 < 0.
Чётный показатель степени:
| (-4)4 = | (-4) · (-4) | · | (-4) · (-4) | = |
| + | + |
= 16 · 16 = 256,
то есть (-4)4 > 0.
следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.
Математика Умножение и деление круглых чисел
Материалы к уроку
Конспект урока
|
24. Умножение и деление круглых чисел на однозначное число
|
|
|
Организационный этап
Добрый день, ребята! Локти – у края, Спинка – прямая. Можно приступать к работе, а она у нас сегодня очень интересная. Мы с вами станем немного волшебниками, а поможет нам в этом наш старый друг — Нолик. На уроке мы будем работать с круглыми числами, мы будем учиться их делить и умножать. |
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Мы начинаем нашу работу, Задание 1 Решите числовые выражения. 3 • 8 -18 Проверьте себя. 74 – 6 • 4 = 50 Задание 2 Расставьте числа в порядке убывания. 58, 50, 42, 27, 4. Проверьте себя. 58, 50, 42, 27, 4. Задание 3 У стола 4 ножки, У 10 столов 40 ножек. Ответ можно найти сложением: |
|
|
Этап усвоения новых знаний
Запишите
40 : 2 = 4 дес. : 2 = 2 дес.=20
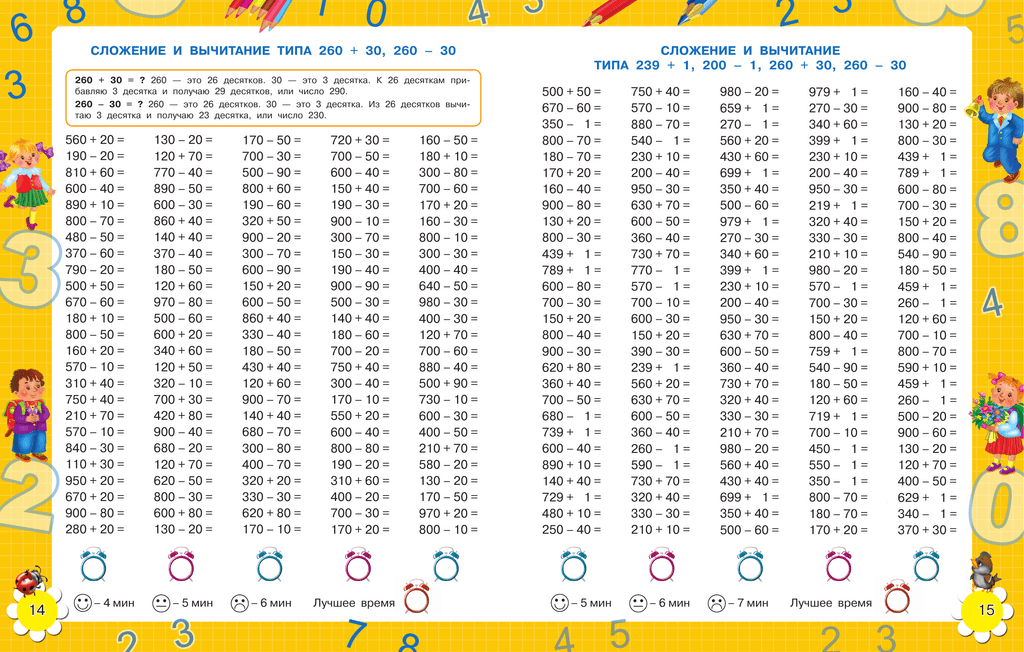
Правило 1: Чтобы найти произведение круглых чисел, можно выполнить умножение, не глядя на нули, а затем приписать справа столько нулей, сколько в обоих множителях вместе. 30 • 3 = 90 Правило 2: При делении круглых чисел (без остатка) можно сначала отбросить поровну нули в делимом и делителе, а потом продолжать деление. 50 : 5 = 10 |
|
|
Этап закрепления новых знаний
Задание 1 Выполните вычисления. 20 • 3 100 : 5 Проверьте себя. 20 • 3 = 60 100 : 5 = 20 |
|
|
Задание 2 Решите задачу. Проверьте себя и оцените свои успехи. В первом действии мы должны узнать, сколько яблонь посадили. Во втором действии мы должны узнать, сколько яблонь стало в колхозном саду. 40 + 50 = 90 яблонь Ответ: в колхозном саду стало 90 яблонь. Задание 3 Вспомните, что такое уравнение? Решите уравнение. Х : 3 = 20 Проверьте себя. Х : 3 = 20 |
|
|
Этап подведения итогов
Ребята, давайте проверим, как вы усвоили изученный материал. Вы сейчас услышите высказывания, если они на ваш взгляд правильные — делайте хлопок, если нет, то – тишина.
МОЛОДЦЫ! |
|
|
Рефлексия
Ребята, если вам всё на уроке было понятно, то нарисуйте в тетради солнышко. Нолик с нами прощается до следующего урока, где мы продолжим работу с круглыми числами. Вы хорошо потрудились. Спасибо за работу! |
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
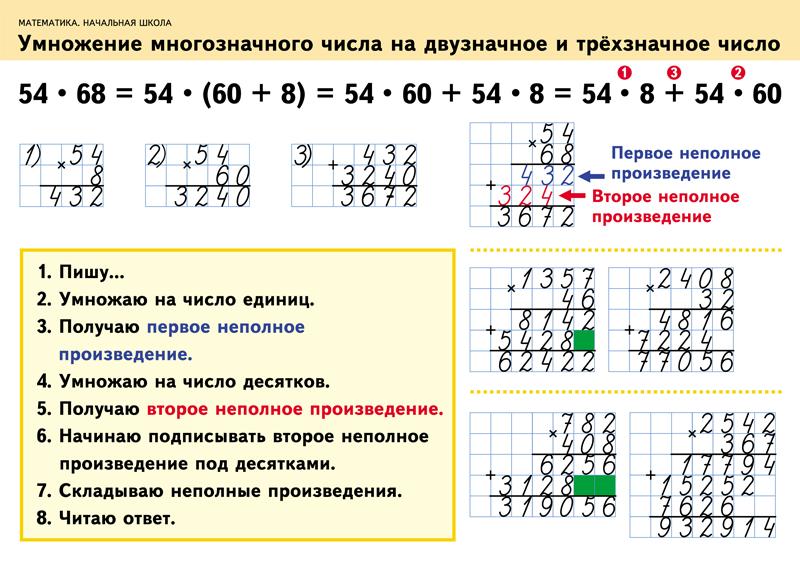
Умножение 2- и 3-значных чисел
Урок 2: Умножение 2- и 3-значных чисел
/en/multiplicationdivision/introduction-to-multiplication/content/
количество, вы увеличиваете много раз. В разделе «Введение в умножение» вы узнали, что умножение может быть способом понять, что происходит в реальной жизни. Например, представьте, что в магазине продаются ящики с грушами. В маленьких коробочках пять груш каждая. Вы покупаете два . Вы можете написать ситуацию следующим образом и использовать для ее решения таблицу умножения на :
В разделе «Введение в умножение» вы узнали, что умножение может быть способом понять, что происходит в реальной жизни. Например, представьте, что в магазине продаются ящики с грушами. В маленьких коробочках пять груш каждая. Вы покупаете два . Вы можете написать ситуацию следующим образом и использовать для ее решения таблицу умножения на :Теперь представьте, что вы решили купить две большие коробки , содержащие 14 груш в каждой. Эта ситуация будет выглядеть так:
Эту задачу решить сложнее. Подсчет груш займет некоторое время. К тому же в таблице умножения нет 14. К счастью, есть способ написать задачу так, чтобы ее можно было разбить на более мелкие части. Это называется укладка . Это означает, что мы будем писать числа друг над другом , а не рядом.
Давайте потренируемся в этой задаче, 14 x 2.
Сначала напишите числа, одно над другим.
 Это хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее.
Это хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее.Затем запишите знак раз к оставшимся числам.
Вместо знака , равного , поставьте черту под числом внизу.
Обратите внимание, как числа выстроены справа от ?
Когда вы пишете задачу на умножение с накоплением, всегда следите за тем, чтобы числа выстраивались таким образом.
Например, давайте рассмотрим другую задачу, 5 x 112. Видите, как 2 находится прямо над 5?
Также обратите внимание, что мы поставили больше числа сверху, хотя это было второе число в нашем исходном выражении.
Всегда решайте задачи на умножение с накоплением одинаково: с большим числом сверху…
Всегда устанавливайте задачи на умножение с накоплением одинаково: с большим числом сверху.
 .. и правильными цифрами выстроились.
.. и правильными цифрами выстроились.
Решение задач на умножение с накоплением
На первый взгляд задачи на умножение с накоплением могут показаться довольно сложными. Не волнуйся! Если вы сможете решить задачи из раздела «Введение в умножение», вы сможете научиться решать и эти задачи. Чтобы умножать большие числа, вам понадобятся те же базовые навыки, что и для умножения маленьких. Вы даже можете использовать такие же инструменты, как раз таблицы .
Давайте посмотрим, как работает решение задач на умножение с накоплением.
Помните пример с двумя коробками, в каждой из которых было по 14 груш? Чтобы узнать, сколько всего груш, мы решим эту задачу: 14 x 2.
Когда вы умножаете сложенные числа, вы начинаете с правой цифры в нижнем числе задачи. Наше нижнее число состоит только из одной цифры: 2.
Мы умножим 2 на верхнее число, 14.
 Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.
Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.Как обычно, решим задачу от вправо влево . Итак, мы умножим 2 на цифру вверху справа. Вот, это 4.
Теперь пришло время решить 2 x 4. Мы можем использовать таблицу умножения.
2 x 4 равно 8. Запишем 8 под 2 и 4.
Теперь умножим 2 на следующую цифру слева: 1.
Теперь решим 2 x 1.
Всякий раз, когда вы умножаете число на 1, это число остается тот же . Итак, 2 x 1 равно 2. Просто чтобы убедиться, мы проверим таблицу умножения.
Напишите 2 под чертой, прямо под 1.
Готово! Всего у нас 28, или двадцать восемь. 14 x 2 = 28.
Давайте потренируемся с другой задачей, 31 x 7.
Всегда начинайте с цифры внизу справа . Здесь это 7.
Сначала умножьте 7 на цифру справа вверху, 1.

7 x 1 равно 7. Напишите 7 непосредственно под цифрами, которые мы только что перемножили.
Далее мы умножаем 7 на следующую цифру слева. Это 3.
Мы воспользуемся таблицей умножения, чтобы найти 7 x 3.
7 x 3 равно 21. Убедитесь, что числа выстроены так, чтобы правая цифра 21, 1, была прямо под 3.
Наш ответ 217. Таким образом, 31 x 7 = 217.
Попробуйте это!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
31 x 3 =
24 x 2 =
40 x 8 =
Использование переноса
На последней странице вы практиковались в умножении чисел, стоящих вертикально. Некоторые проблемы требуют дополнительного шага. Давайте рассмотрим следующую задачу:
Если вы попытаетесь умножить 9 x 5, вы заметите, что нет места для записи произведения, 45. Когда произведение двух чисел равно больше, чем 9 , вам нужно будет использовать технику, называемую , несущей . Если вы знаете, как складывать большие числа, возможно, вы помните и об использовании переноса. Давайте посмотрим, как это работает в умножении.
Если вы знаете, как складывать большие числа, возможно, вы помните и об использовании переноса. Давайте посмотрим, как это работает в умножении.
Давайте попробуем решить задачу, которую мы только что рассмотрели, 29 x 5.
Как обычно, мы начнем с умножения 5 на верхнюю правую цифру, 9.
Согласно нашей таблице умножения , 5 x 9 равно 45, но нет места для записи обеих цифр под 5 и 9.
Запишем правую цифру 5 под чертой…
Запишем правую цифру 5 под чертой… тогда запишем левую цифру , 4, до следующего набора цифр в задаче.
Видишь, как это работает? Мы умножили 5 и 9, чтобы получить 45. Мы поместили 5 под чертой, перенесли 4 и поместили ее над следующим набором цифр.
Теперь пришло время для следующего шага. Это то же самое, что и с любой другой задачей на умножение. Мы умножим 5 х 2,
5 х 2 = 10. Но 10 под чертой пока писать не будем — есть еще один шаг.

Помните номер, который мы носили, 4?
Мы должны к добавить к нашему продукту, 10.
4 + 10 равно 14.
Мы напишем 14 под чертой.
Итого 145. Теперь мы знаем, что 29 х 5 = 145.
Давайте попробуем решить еще одну задачу. 208 х 6,
Сначала мы умножаем нижнее число 6 на цифру справа вверху. Это 8.
6 x 8 равно 48.
Запишем 8 под чертой…
Запишем 8 под чертой… и перенесем 4. Мы поместим его над следующей цифрой.
Следующая цифра 0.
Все, что умножается на ноль, равно 0, поэтому мы знаем, что 6 x 0 = 0.
Помните, мы еще не пишем этот 0 под чертой. Мы должны добавить его к 4, которые мы только что перенесли.
4 + 0 = 4. Под чертой напишем 4.
Наконец, мы умножаем 6 на 2.
6 x 2 = 12, поэтому мы напишем 12 под чертой.

Готово! Ответ: 1248, или одна тысяча двести сорок восемь. 208 x 6 = 1248.
Попробуйте!
Сложите и решите эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
25 х 9=
98 x 2 =
103 x 5 =
Умножение больших чисел
На последних нескольких страницах вы практиковались в умножении больших чисел на маленькие. Что произойдет, если вам нужно умножить два больших числа?
Например, представьте, что ваш счет за мобильный телефон составляет 43 доллара в месяц . В году 12 месяцев, поэтому, чтобы узнать, сколько вы платите за свой телефон каждый год, вы можете решить 43 x 12. Вы должны написать выражение следующим образом:
На первый взгляд эта проблема может показаться сложной, но не беспокойтесь. Если вы можете умножать маленькие числа, вы можете умножать и большие. Все, что вам нужно сделать, это разделить эту большую проблему на несколько более мелких. Как всегда, вы можете использовать свою таблицу умножения на , чтобы помочь.
Как всегда, вы можете использовать свою таблицу умножения на , чтобы помочь.
Чтобы решить такую большую задачу, начните с тех же шагов, которые вы используете для решения любой другой задачи на умножение.
Как всегда, вы начинаете с цифры справа внизу. Вот, это 2.
Умножим на цифру справа вверху, 3.
Благодаря нашей таблице умножения мы знаем, что 3 x 2 равно 6.
Мы запишем 6 под линия, крайняя правая.
Далее умножаем 2 x 4.
2 x 4 равно 8.
Напишите 8 под чертой, прямо под 4.
- 90 OK. Первая половина задачи решена.
Теперь пришло время снова взглянуть на нижний номер.
Мы собираемся умножить следующую цифру. Это 1.
Сначала умножьте 1 на верхнее число справа. Здесь это 3.
1 x 3 равно 3… но мы не собираемся писать 3 в обычном месте.

Вместо того, чтобы писать 3 в справа , как мы обычно делаем…
Вместо того, чтобы писать 3 в справа , как мы обычно делаем… это на одно место левее, под вторым набором цифр.
Рекомендуется отметить место, которое вы оставили пустым. Таким образом, вы будете знать, что случайно ничего туда не запишете. Мы добавим 0, так как ноль такой же, как ничего .
Теперь давайте умножим последний набор чисел. Это 1 x 4.
1 x 4 = 4. Мы напишем 4 под чертой, слева от 3, которые мы только что написали.
Последний шаг. Чтобы получить окончательный ответ, нам нужно к добавить чисел, которые мы только что получили в результате умножения.
Как всегда, мы начнем добавлять справа.
6 + 0 равно 6. Мы напишем 6 под чертой.
Далее, 8 + 3.
8 + 3 равно 11.
 Поскольку 11 — двузначное число, нам придется переносить.
Поскольку 11 — двузначное число, нам придется переносить.Запишите правую цифру 1 под 8 и 3…
Запишите левую цифру 1 под 8 и 3… затем перенесите правую цифру и поместите ее над цифрой левый.
Наконец, мы добавим 4 к только что перенесенной 1.
4 + 1 равно 5.
Готово! Итого 516. Другими словами, 43 x 12 = 516.
Попробуйте!
Сложите и перемножьте эти двузначные числа. Затем проверьте свой ответ, введя его в поле.
33 x 21 =
52 x 17 =
81 x 34 =
Умножение двух трехзначных чисел
Умножение больших чисел всегда работает одинаково, независимо от того, сколько цифр в числах. Когда вы умножаете, будьте осторожны, записывая числа в правильных местах. Давайте рассмотрим задачу с двумя 3-значные числа , чтобы увидеть, как это работает с еще большими числами.
Давайте попробуем решить эту задачу: 601 x 243.

Как всегда, начнем с умножения нижней правой цифры на верхнюю правую цифру. Итак, 3 x 1.
Благодаря нашей таблице умножения мы знаем, что 3 x 1 равно 3. Запишите число 3 под чертой справа.
Теперь умножьте 3 на следующее число, 0.
Любое число, умноженное на ноль, равно 0, поэтому напишите 0 под чертой, рядом с 3.
Далее, 3 x 6.
3 x 6 = 18. Напишите 18 под чертой.
Мы закончили с первой цифрой нижнего числа.
Затем умножьте на второе число внизу, 4.
4 x 1 равно 4. Помните, что вы не собираетесь писать 4 до конца вправо.
Вместо этого напишите 4 на одну позицию левее под вторым набором цифр.
Чтобы все было выровнено, мы поместим ноль в качестве заполнителя справа от четырех.
Теперь давайте перейдем к следующему числу сверху — 0.

4 x 0 равно 0. Напишите 0 под чертой.
Затем умножьте 4 на последнюю цифру верхнего числа — 6.
4 x 6 равно 24. Напишите 24 под чертой.
Мы готовы умножить на последнюю цифру нашего нижнего числа — 2.
Как всегда, начните с верхней правой цифры, 1.
2 x 1 равно 2.
Напишем 2 под чертой, через два пробела справа.
Обратите внимание, куда мы поставили 2.
Когда мы умножили на первую цифру в нижнем числе…
Когда мы умножили на первую цифру в нижнем числе. , мы выстроили товар до упора вправо .
Когда мы умножали на вторую цифру …
Когда мы умножали на вторую цифру … мы записывали произведение на один пробел слева.
Теперь, когда мы умножили на третью цифру .
 ..
..Теперь, когда мы умножили на третью цифру … мы поместили произведение на два пробела слева от
Возможно, вы заметили закономерность. Каждый раз, когда мы умножали на новую цифру, мы записывали произведение на одну цифру дальше влево. Это верно независимо от того, сколько цифр в числах, на которые вы умножаете.
Вернемся к нашей проблеме. Мы просто умножили 2 x 1.
Следующая цифра 0.
2 x 0 равно 0. Напишите 0 под чертой.
Наконец, умножьте 2 x 6.
2 x 6 равно 12. Напишите 12 под чертой.
Время добавить. Как всегда, начните с крайних правых цифр. Здесь это означает, что мы добавляем 3 + 0 + 0.
3 + 0 + 0 = 3. Напишите 3 непосредственно под цифрами, которые мы только что добавили.
Далее мы добавим 0 + 4 + 0.
0 + 4 + 0 равно 4.

Теперь следующий набор цифр, 8 + 03 2.
- 5 9009 8 + 0 + 2 = 10. 10 — двузначное число, поэтому нам нужно нести . Напишите 0 под цифрами, которые мы только что добавили, и поместите 1 над следующим набором цифр.
Пришло время добавить 1, которую мы только что перенесли. Это означает, что мы находим 1 + 1 + 4 + 0.
1 + 1 + 4 + 0 = 6. Напишите 6 под чертой.
Далее, 2 + 2.
2 + 2 = 4. Напишите 4 под чертой.
Слева только одна цифра — 1.
Один плюс ничего равно 1, поэтому под чертой напишем 1.
Наконец-то мы закончили! Всего у нас 146 043, или сто сорок шесть тысяч сорок три. 601 х 243 = 146 043.
Какое огромное количество! Если эта проблема показалась вам сложной, не волнуйтесь. Вам редко придется умножать такие большие числа. Когда вы это сделаете, вы всегда можете воспользоваться калькулятором. Тем не менее, хорошо знать, как это сделать. Если вы сможете умножить эти проблемы, вы сможете умножить что угодно.
Тем не менее, хорошо знать, как это сделать. Если вы сможете умножить эти проблемы, вы сможете умножить что угодно.
Практика!
Практика умножения больших чисел. Затем проверьте свой ответ, введя его в поле.
Набор 1
13 x 3 =
42 x 4 =
21 x 9 =
63 x 2 =
52 x 3 =
Набор 4 3 90 90
24 х 8 =
63 x 7 =
18 x 6 =
35 x 9 =
Набор 3 17 х 12 =
55 х 48 =
ПродолжатьПредыдущий: Введение в умножение
Далее:Видео: умножение
/en/multiplicationdivision/video-multiplication/content/
Умножение и деление: определение, правила, свойства
- Автор Прия_Сингх
- Последнее изменение 24-01-2023
Арифметические операции математики включают сложение, вычитание, умножение и деление на все типы действительных чисел, включая целые числа.
В математике термин умножение является одной из основных операций и означает многократное сложение числа относительно другого числа. Символ умножения — \(×.\). В этой статье мы предоставим подробную информацию об умножении и делении. Продолжайте читать, чтобы узнать больше!
Умножение: Умножение используется для нахождения произведения двух или более чисел. Умножение также известно как многократное сложение.
Пример: Когда вы хотите умножить числа \(4 \times 12 = 48\) или \(12 + 12 + 12 + 12 = 48.\)
Деление: Деление — это операция, обратная умножению. Так пытаются определить, сколько раз одно число содержится в другом.
Мы знаем, что деление \(20\) на \(5\) означает нахождение числа, которое при умножении на \(5\) дает нам \(20. \) Такое число равно \(4.\)
\) Такое число равно \(4.\)
Следовательно , мы пишем \(20 \div 5 = 4\) или \(\frac{{20}}{5} = 4.\)
Аналогично, деление \(36\) на \( – 9\) означает нахождение число, которое при умножении на \( – 9\) дает \(\left( {36} \right).\) Такое число равно \( – 4.\)
Поэтому мы пишем \(36 \div \left( { – 9} \right) = – 4\) или \(\frac{{36}}{{ – 9}} = – 4\)
Деление \( – 35\) на \(\left( { – 7} \right)\) означает, какое число нужно умножить на \(\left( { – 7} \right)\), чтобы получить \(\left( { – 35 } \right).\)
Таким числом является \(5.\)
Следовательно, \(\left( { – 35} \right) \div \left( { – 7} \right) = 5\) или \(\frac{{ – 35}}{{ – 7}} = 5.\)
Делимое: Число, которое нужно разделить, называется делимым.
Делитель: Число, которое делится, называется делителем.
Частное: Результат деления известен как частное.
Остаток: Число, оставшееся после деления, называется остатком.
Здесь \(r\) остаток, очевидно, \(r = a – bq.\)
Используя эти термины, алгоритм деления можно переформулировать следующим образом:
\({\rm{Дивиденд}} = { \rm{Делитель}} \times {\rm{Частное}} + {\rm{Остаток}}\)
Пример: Если мы разделим \(26\) на число \(6,\), то делимое равно \(26,\) делитель равен \(6,\), частное равно \(26,\), а остаток равен \(2.\)
Правила умножения и деления следующие:
Умножение Чтобы умножить числа, мы следуем данным правилам:
Правило 1: Произведение чисел противоположных знаков равна аддитивной обратной величине произведения их модулей.
Пример: \(7 \times \left( { – 4} \right) = – \left( {7 \times 4} \right) = – 28\)
\(\left( { – 8} \right) \times 5 = — \left( {8 \times 5} \right) = — 40\)
Правило 2: Произведение двух чисел с одинаковыми знаками равно произведению их абсолютных значений.
Пример: \(7 \times 12 = 84\)
\(\left( { – 8} \right) \times \left( { – 13} \right) = 8 \times 13 = 104\)
Вы знаете, что когда делимое отрицательно и делитель отрицателен, частное положительно. Если делимое — отрицательное число, а делитель — положительное число, то частное — отрицательное число.
Таким образом, мы имеем следующие правила деления чисел:
Правило \(1:\) Частное двух чисел, как положительных, так и отрицательных, является положительным числом, равным частному соответствующих основных значений чисел.
Таким образом, мы разделяем их значения независимо от их знака и ставим знак плюс в частном для деления двух чисел с одинаковыми символами.
Правило \(2:\) Частное положительного и отрицательного чисел является отрицательным числом. Абсолютное значение равно частному соответствующих основных значений чисел.
Таким образом, мы делим их значения независимо от их знака и ставим знак минус в частное для деления чисел с разными знаками.
Свойства умножения и деления следующие:
Умножение: Ниже приведены свойства умножения:
. Другими словами,
, если \(a\) и \(b\) — любые два целых числа, то \(a \times b = b \times a\)
2. Умножение на ноль: Если \(a\) — любое целое число, то \(a \times 0 = 0 \times a = 0.\)
Другими словами, произведение любого целого числа на ноль всегда равен нулю.
3. Существование тождества умножения: Если \(a\) является целым числом, то \(a \times 1 = a = 1 \times a.\)
Другими словами, произведение любого целого числа и \(1\) — это само число.
Число \(1\) известно как идентификатор умножения или элемент идентификации для умножения целых чисел, поскольку оно не изменяет идентичность (значение) чисел во время операции умножения.
4. Ассоциативность: если \(a,\,c\) целые числа, то
\(\left( {a \times b} \right) \times c = \left( {b \times c} \право)\)
Умножение целых чисел ассоциативно; то есть произведение трех действительных чисел не меняется при изменении их расположения.
5. Дистрибутивность умножения над сложением: Если \(a,\,b,\,c\) любые три целых числа, то
\(a \times \left( {b + c} \right) = a \times b + a \times c\)
\(\left( {b + c} \right) \times a = b \times a + c \times a\)
Умножение целых чисел опережает их сложение.
Деление: Ниже приведены некоторые свойства деления чисел:
1. Если \(a\) и \(b\) являются целыми числами, то \(a \div b\) равно не обязательно целое число.
Пример: \(14 \div 2 = 7.\) Здесь частное является целым числом.
Но в \(15 \div 4,\) мы видим, что частное не является целым числом. Здесь результат равен
\(\frac{{15}}{4} = 3\frac{3}{4}.\) частное равно \(3;\) остаток равен \(3\)
2. Если \(a\) — целое число, отличное от \(0,\), то \(a \div a = 1.\)
3. Для каждого целого \(a,\) имеем \(a \ div 1 = a.\)
4. Если \(a\) ненулевое целое, то \(0 \div a = 0\)
5. Если \(a\) целое, то \( a \div 0\) не имеет смысла.
6. Если \(a,\,b,\,c\) целые числа, то
\(a > b \Rightarrow a \div c > b \div c,\), если \(c\) положительно.
\(a > b \Rightarrow a \div c > b \div c,\), если \(c\) отрицательно.
Формулы умножения и деления следующие:
УмножениеФормулы умножения чисел приведены ниже в таблице:
| 9 Тип 10 90 90 0009 Операция | Результат | Пример | |
| Положительный \( \times \) Положительный | Умножение | Положительный \(\left( + \right)\) | \(1 \times 7 = 7\) |
| Отрицательное \( \times \) Отрицательное | Умножить | Положительное \(\left( + \right)\) | \(\left( { – 1} \right) \times \left( { – 7} \right) = 7\) |
| Положительное \( \times \) Отрицательное | Умножить | Отрицательное \(\left( + \right)\) | \(1 \times \left( { – 7} \right) = – 7\) |
| Отрицательное \( \times \) Положительное | Умножить | Отрицательное \(\left( + \right)\ ) | \(\left( { – 1} \right) \times 7 = – 7\) |
В случае умножения чисел нужно умножать числа без знака.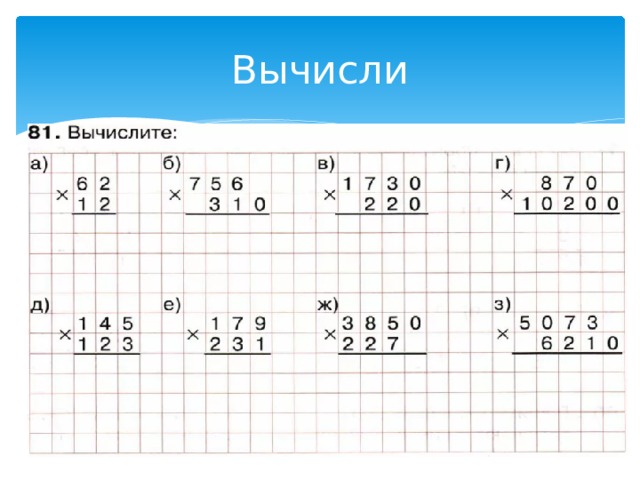 После того, как продукт приобретен, отметьте символ в соответствии с правилом умножения.
После того, как продукт приобретен, отметьте символ в соответствии с правилом умножения.
Формулы деления чисел приведены ниже в таблице:
| Тип чисел | Операция 04| Результат | Пример | |
| Положит. 2\ ) | |||
| Отрицательное \( \div \) Отрицательное | Разделить | Положительное \(\left( + \right)\) | \(\left( { – 12} \right) \div \left( { – 6} \right) = – 2\) |
| Положительный \( \div \) Отрицательный | Разделить | Отрицательный \[\left( – \right)\] | \(12 \div \left( { – 6} \right) = – 2\) |
| Отрицательное \( \div \) Положительное | Разделить | Отрицательное \[\left( – \right)\ ] | \(\left( { – 12} \right) \div 6 = – 2\) |
То же, что и умножение, вы должны разделить числа без знака, а затем дать символ в соответствии с правило, как указано в таблице.
Деление двух чисел с одинаковыми знаками дает положительное частное, а деление двух чисел с разными знаками дает отрицательное частное.
Умножение: При умножении четных чисел отрицательных целых чисел результат всегда положительный.
\(\влево(-\вправо) \раз \влево(-\вправо)\влево(-\вправо) \раз \влево(-\вправо) = \влево(+\вправо)\)
Деление: На каждый факт умножения приходится два факта деления.
Пример: Для таблицы номер 5 фактами деления являются \(10 \дел 5 = 2,\,25 \дел 5 = 5\) и \(50 \дел 5 = 10\) и \(5 \ умножить на 2 = 10,\,2 \умножить на 5 = 10.\)
Q.1. Умножьте \(475\) на \(64\), используя свойство дистрибутивности.
Ответ: У нас есть, \(475 \times 64\)
\( = \left( {400 + 70 + 5} \right) \times 64\)
\( = 400 \times 64 + 70 \х 64 + 5 \х 64\) [Используя дистрибутивность]
\( = 25600 + 4480 + 320 = 30400\)
Q. 2. Найдите число, которое при делении на \(46\) дает частное \(11\) и остаток \(18.\)
2. Найдите число, которое при делении на \(46\) дает частное \(11\) и остаток \(18.\)
Ответ: У нас есть,
Делитель \(= 46,\) Частное \(= 11\) и Остаток \(= 18.\)
Нам нужно найти делимое. По алгоритму деления имеем
\({\rm{Дивиденд}} = {\rm{Делитель}} \times {\rm{Частное}} + {\rm{Остаток}}\)
\(\Rightarrow {\ rm{Дивиденд}} = 46 \умножить на 11 + 18\)
\( = 506 + 18 = 524.\)
Следовательно, требуемый ответ равен \(524.\)
Q.3. Найдите произведение \(4 \times 4957 \times 25.\)
Ответ: Заметим, что
\(4 \times 25 = 100\)
Таким образом, мы можем расставить числа, чтобы найти желаемый продукт
\(4 \times 4925 \times 25 = \left( { 4 \times 25} \right) \times 4957 = 100 \times 4957 = 495700\)
Следовательно, искомый ответ: \(495700.\)
Q.4. Найдите значение: \(\left[ {32 + 2 \times 17 + \left( { – 6} \right)} \right] \div 15\)
Ответ: У нас есть,
\(\left[ {32 + 2 \times 17 + \left( { – 6} \right)} \right] \div 15\)
\( = \left[ {32 + 34 \div \left( { – 6} \right)} \right] \div 15 = \left( {66 – 6} \right) \div 15 = 60 \div 15 = \frac{{60}}{{15}} = 4\)
Следовательно, требуемый ответ равен \(4. \)
\)
Q.5. Определить произведение наибольшего числа четырехзначных и наибольшего числа трехзначных.
Ответ: Мы знаем, что наибольшее четырехзначное число равно \(9999\), а наибольшее трехзначное число равно \(999.\)
\(\следовательно \) Требуемый продукт \( = 9999 \times 999\)
\( = 9999 \times \left( {1000 – 1} \right)\)
\( = 9999 \times 1000 – 9999 \times 1\,\,\,\left[ {\ ,a \times \left( {b – c} \right) = a \times b – a \times c} \right]\)
\( = \left( {1000 – 1} \right) \times 1000 – \влево( {1000 — 1} \вправо) \в 1\)
\( = 1000 \в 1000 — 1000 \время 1 — \влево( {1000 \время 1 — 1 \время 1} \вправо)\)
\(\left[ {\,\left( {a – b} \right) \times c = a \times c – b \times c} \right]\)
\( = 1000000 – 1000 – 10000 + 1\) )
\(= 1000000 – 11000 = 9989001\)
Итог
Умножение помогает нам найти произведение двух или более чисел. Это также известно как повторное добавление.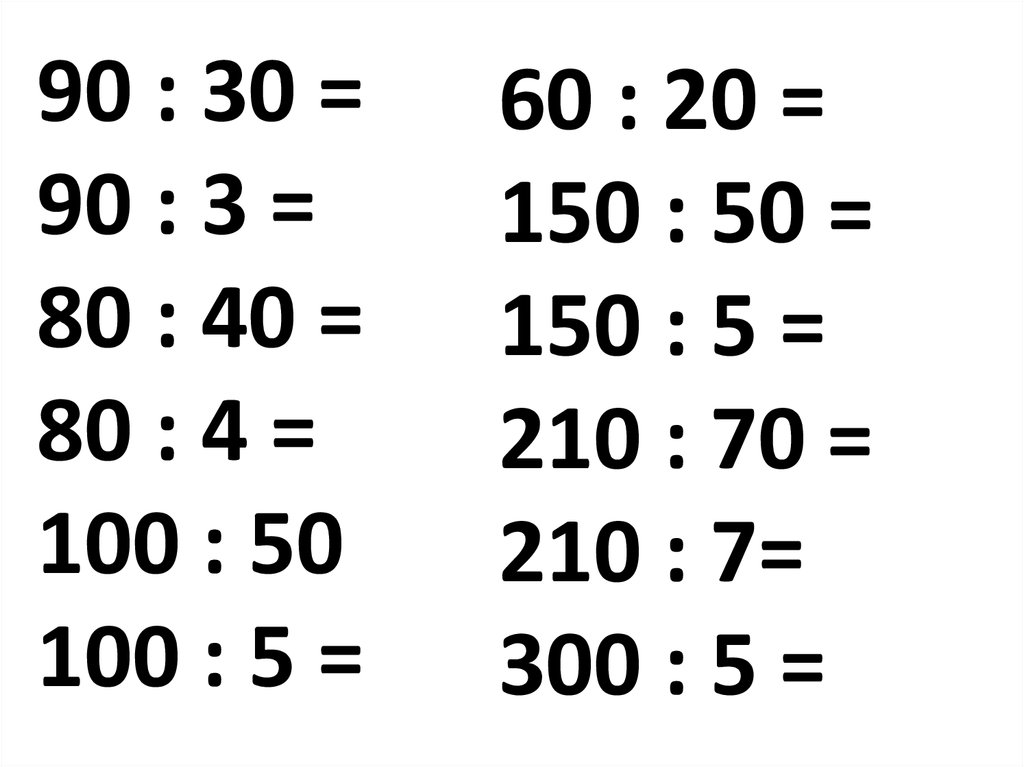 Деление помогает учащимся определить, сколько раз одно число содержится в другом. Деление также известно как повторное вычитание. Для деления используется символ \( \div .\). В делении используются четыре основных термина. Основными терминами, используемыми при делении, являются делимое, делитель, частное и остаток.
Деление помогает учащимся определить, сколько раз одно число содержится в другом. Деление также известно как повторное вычитание. Для деления используется символ \( \div .\). В делении используются четыре основных термина. Основными терминами, используемыми при делении, являются делимое, делитель, частное и остаток.
Q.1. Как легко умножать и делить?
Ответ: Умножение
Например: Когда вы хотите умножить число \(5\) на любое четное число: \(5 \times 4 = \)
Вы должны взять число, которое умножается на \(5\) и разрезается пополам, что означает, что число \(4\) станет \(2.\)
Добавьте число ноль рядом с числом \(2,\), что означает, что вы получили число \(20,\), т. е. \(5 \times 4 = 20.\)
Если вы хотите умножить число \(5 x 4 = 20.\) на любое нечетное число:
Например: \(5 x 3 = \)
Вы должны вычесть единицу из числа, умноженного на \( 5,\), что означает число \(3 – 1 = 2. \)
\)
Теперь снова нужно разделить пополам число \(2\), что означает \(2 – 1 = 1,\), и добавить цифру \ (5\) рядом с цифрой \(1,\), которая дает \(5 \times 3 = 15\)
Деление
Например: Деление на \(5:\) Здесь вам нужно просто- просто умножьте число на \(2\), а затем разделите полученное произведение на число \(10.\)
Если вы делите число \(65432\) на \(5\), то
Вы будете писать как \(65432 \div 5 = \left( {65432 \times 2} \right) \div 10 = 130864 \ дел 10 = 13086,4\)
Q.2. Объясните умножение и деление на примере?
Ответ: При умножении чисел мы находим произведение заданных чисел путем их умножения.
Пример: \(3 \times 10 = 30\) или \(10 + 10 + 10 = 30\)
При делении мы делим числа, чтобы получить недостающий множитель, когда заданы два других множителя. Деление также известно как повторное вычитание.
Пример: \(56 \дел 7 = 8,\,56 \дел 8 = 7\) или \(56 – 8 – 8 – 8 – 8 – 8 – 8 – 8. \)
\)
Q .3. Какие \(4\) способы показать умножение?
Ответ: 1. Умножьте числа, используя многократное сложение
2. Умножьте числа, используя метод длинного умножения.
3. Умножьте числа, используя метод сетки.
4. Умножить числа, разделив числа на единицы, десятки, сотни (по разрядности).
Q.4. Какие символы используются для умножения?
Ответ: Символ, который мы используем для представления умножения, — это знак креста \(\left( \times \right),\), а иногда мы также используем точку \(\left( * \right) \) для представления произведения чисел.
Q.5. Какие символы обозначают умножение и деление?
Ответ: Символ, который мы используем для умножения, — это знак креста \(\left( \times \right),\), а иногда мы также используем точку \(\left( \cdot \right) \) или \(\left( * \right)\) для представления произведения чисел.


 Сложим, сколько яблонь росло, и сколько посадили.
Сложим, сколько яблонь росло, и сколько посадили.
 Это хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее.
Это хорошая привычка всегда писать большее число сверху. Если вы этого не сделаете, решить проблему будет сложнее. .. и правильными цифрами выстроились.
.. и правильными цифрами выстроились. Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.
Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.


 Поскольку 11 — двузначное число, нам придется переносить.
Поскольку 11 — двузначное число, нам придется переносить.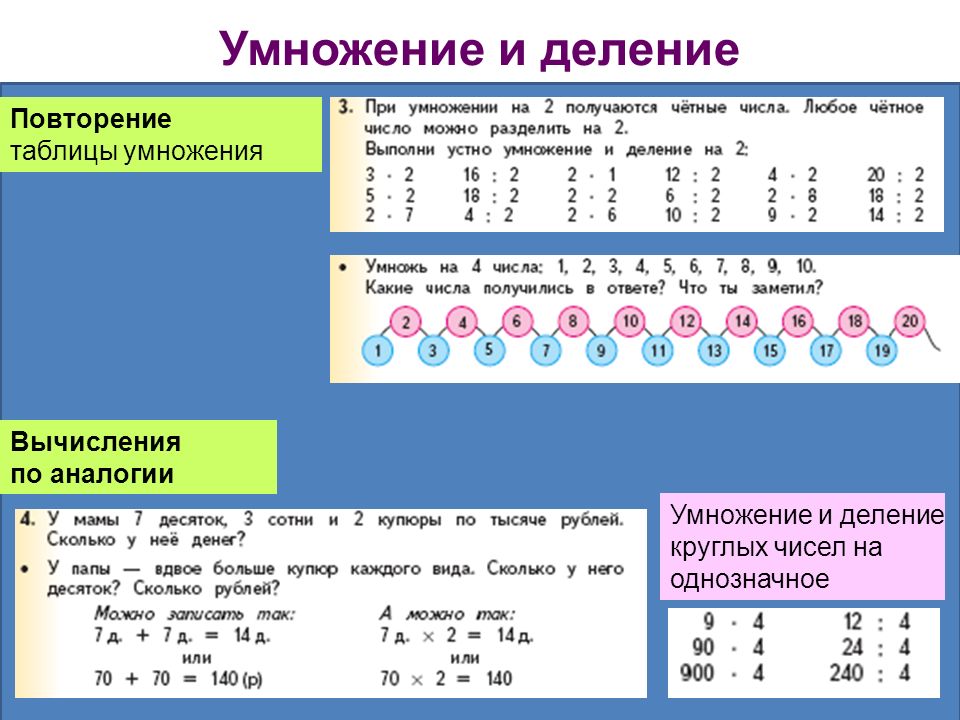

 ..
..