Умножение и деление на 0 3 класс: Умножение и деление 0 — урок. Математика, 3 класс.

Содержание

а, а : 1, 0 : а

Этап усвоения новых знаний

Ребята, вспомните, что такое умножение?
Умножение – это сложение одинаковых слагаемых

Замените в следующих примерах произведение суммой и запишите.

5 · 3 =
5 · 2=
5 · 1=

Проверьте себя.

5 · 3 = 5 + 5 + 5 + 5
5 · 2 = 5 + 5
5 · 1 = ?
5 · 0 = ?

Удалось ли заменить сложением последние два примера?
Это особые случаи.
Нельзя взять число слагаемым один раз. Поэтому применим переместительное свойство умножения:
1 · 5 = 1 + 1 + 1 + 1 + 1 = 5

Кроме табличных случаев умножения и деления в математике, существуют случаи, которые называют особыми — это

математические законы, которые нужно знать: при умножении любого числа на 1, получается то число, которое умножали.

В математике обозначают любое число латинской буквой а.
Запишите этот вывод формулой.
а · 1 = а

Запомните!
Вместо буквы а мы можем подставить любое число.

Рассмотрим подробно пример 5 · 0 = ?
К данному случаю можно применить переместительное свойство умножения.
0 · 5 = 0 + 0 + 0 + 0 + 0 = 0

Второй математический закон, который нужно сегодня запомнить:
Произведение считается равным нулю, при умножении на 0.

Запишите этот вывод формулой.

а · 0 = 0

Запомните!
Вместо буквы а, мы можем подставить любое число.

Лучшему запоминанию новых случаев умножения будет способствовать создание наглядного образа.

Множитель 1 не изменяет число, его можно представить зеркальцем.
Как бы отражает второй множитель, не изменяя его.

Нуль – это шапка – невидимка. Он при умножении покрывает второй множитель и делает его невидимым.

Давайте вспомним, что такое деление.
Деление — это действие, обратное умножению.
Каждому примеру на умножение можно составить два обратных примера на деление.
Рассмотрим подробно следующие случаи деления:

а : а = ?
а : 1 = ?
0 : а = ?

Запишите пример 5 · 1 = ?
Проверим 5 · 1 = 5

Каждому примеру на умножение можно составить два обратных примера на деление.
Составим и запишем.

5 : 5 = ?
Проверим 5 : 5=1

Делаем вывод:
При делении числа на то же самое число получается единица. Запишем буквенное выражение или формулу

а : а = 1
ЗАПОМНИТЕ!

Запишем второй пример на деление.
5 : 1 = ?

Проверим
5 : 1 = 5

Делаем вывод:
При делении числа на 1 получается то же самое число
Запишем буквенное выражение или формулу
а : 1 = а

Решим ещё один пример на деление, запишите
0 : 5 = ?….
Это значит, надо найти число, при умножении которого на 5 получится 0.
х · 5 = 0

Это будет число 0. Значит, 0 : 5 = 0…..

Делаем вывод:
При делении 0 на любое число получается 0.
Запишем буквенное выражение или формулу
0 : а = 0

Этап закрепления новых знаний

Задание 1

Выполните вычисления.

91 ∙ 1 =
64 + 0 =
18 ∙ 0 =
1 ∙ 35 =
25 + 1 =
0 ∙ 361 =
72 ∙ 0 =
54 ∙ 1 =
31 — 0 =
0 ∙ 159 =
1 ∙ 76 =
98 — 1 =

Проверьте себя и оцените свои успехи.

91 ∙ 1 = 91
64 + 0 = 64
18 ∙ 0 = 0
1 ∙ 35 = 35
25 + 1 = 26
0 ∙ 361 = 0
72 ∙ 0 = 0
54 ∙ 1 = 54
31 — 0 = 31
0 ∙ 159 = 0
1 ∙ 76 = 76
98 — 1 = 97

Задание 2

Найдите числовые выражения, при решении которых допущена ошибка. Запишите эти выражения, сделав вычисления правильно.

1 · 15 = 15
3 · 0 = 3
19 : 19 = 1
23 : 1 = 1
26 : 26 = 1
12 + 0 = 0

17 — 0 = 17

Проверьте себя и оцените свои успехи.

3 · 0 = 0
23 : 1 = 23
12 + 0 = 12

Этап подведения итогов

Давайте повторим:

При умножении любого числа на 1 получается число, которое умножаем.
При умножении любого числа на 0 получается 0.
При делении числа на то же самое число получается единица.
При делении числа на 1 получается то же самое число.
При делении 0 на любое число получается 0.

Запомните! Делить на нуль нельзя!

Рефлексия

Выберите смайлик, который более всего соответствует вашему пониманию изученных сегодня на уроке правил и нарисуйте его у себя в тетради.

Спасибо за работу, вы хорошо потрудились!

Урок математики в 3 классе. Тема урока: «Деление 0 на число. Невозможность деления на 0». | План-конспект урока по математике (3 класс) по теме:

Учебник: «Математика» 3 класс М.И. Моро

Цели урока: создать условия для формирования умения делить 0 на число.

Задачи урока:

раскрыть смысл деления 0 на число через связь умножения и деления;
развивать самостоятельность, внимание, мышление;
формировать навыки решения примеров на табличное умножение и деление.

Для достижения цели урок был разработан с учётом деятельностного подхода.

Структура урока включала в себя:

Орг. момент, целью которого было позитивно настроить детей на учебную деятельность.
Мотивация позволила актуализировать знания, сформировать цели и задачи урока. Для этого были предложены задания на нахождение лишнего числа, классификацию примеров на группы, добавление недостающих чисел. В ходе решения этих заданий, дети столкнулись спроблемой: нашёлся пример, для решения которого не хватает имеющихся знаний. В связи с этим дети самостоятельно сформулировали цель и поставили перед собой учебные задачи урока.
Поиск и открытие нового знания дал возможность детям предложить различные варианты решения задания. Основываясь на ранее изученный материал, они смогли найти верное решение и прийти к выводу, в котором сформулировали новое правило.
Во время первичного закрепления ученики комментировали свои действия,работая по правилу, дополнительно были подобраны свои примеры на это правило.
Для автоматизации действий и умения пользоваться правилам в нестандартных заданиях дети решали уравнения, выражения в несколько действий.
Самостоятельная работа и проведенная взаимопроверка показали, что большинство детей тему усвоили.
Во время рефлексии дети сделали вывод, что поставленная цель урока достигнута и оценили себя с помощью карточек.

В основе урока лежали самостоятельные действия учащихся на каждом этапе, полное погружение в учебную задачу. Этому способствовали такие приёмы, как работа в группах, само- и взаимопроверка, создание ситуации успеха, дифференцированные задания, саморефлексия.

Урок математики в 3 классе.

Тема урока: «Деление 0 на число. Невозможность деления на 0»

Цели урока: создать условия для формирования умения делить 0 на число.

Задачи урока:

раскрыть смысл деления 0 на число через связь умножения и деления;
развивать самостоятельность, внимание, мышление;
формировать навыки решения примеров на табличное умножение и деление.

Ход урока.

Организационный этап.

Проверьте свою готовность к уроку, сядьте прямо.
Потрите свои ушки, чтобы кровь активнее поступала в мозг. Сегодня у вас будет много интересной работы, с которой, я уверена, вы справитесь на отлично.

(слайд 1; 2; 3)

Веселый прозвенел звонок,

Мы начинаем наш урок.

Все ли правильно сидят,

Все внимательно глядят?

Каждый хочет получать

Только лишь оценку пять!

— Откройте свои тетради, запишите сегодняшнее число. (слайд 4) Что вы можете сказать о числе 20? (Оно двузначное; оно чётное; состоит из разряда десятков и разряда единиц).

— Сколько десятков и сколько единиц в нём? (2 десятка и 0 единиц.).

Устный счёт.

Игра «Найди лишнее число» (слайд 5)

-Из каждого столбика выберите «лишнее число»

2. Найдите площади фигур: (слайд 6)

3.Арифметический диктант:

Какое число надо умножить на 7, чтобы получить 42?
Назовите число, которое меньше 24 на 6?
Из какого числа надо вычесть 18, чтобы получить 3?
Во сколько раз 4 десятка больше 5?
Найдите произведение 9 и 3.
Делимое 36, частное 6. Чему равен делитель?
Увеличьте 8 в 6 раз.
На какое число надо разделить 28, чтобы получить 7?

— Запишите только ответы.

(Взаимопроверка: 6, 18, 21, 8, 27, 6, 48, 4.) – (слайд 7)

4.Индивидуальная работа (работа по карточкам, см. приложения)

5. Создание проблемной ситуации
Задания в парах:
— расставьте примеры в 2 группы:

Почему так распределили? (с ответом 4 и 5)

— решите примеры:
8·7-6+30:6=
28:(16:4)·6=
30-(20-10:2):5=
30-(20-10·2):5=

— Что вы заметили? Есть ли здесь лишние примеры?
— Все ли примеры вы смогли решить?
— У кого возникли затруднения?
— Чем этот пример отличается от остальных?
— Если кто-то решил, то молодец. Но почему не все смогли справиться с этим примером?

6.Постановка учебной задачи.
Здесь есть пример с 0. А от 0 можно ожидать разные фокусы. Это необычное число.
Вспомните, что вы знаете про 0? (а·0=0, 0·а=0, 0+а=а)·
Приведите примеры.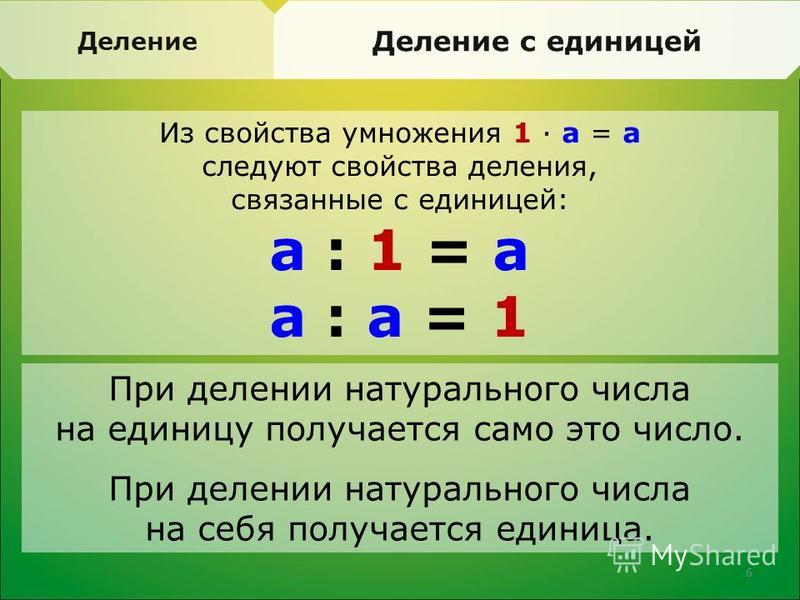
Посмотрите, какой он коварный: когда его прибавляют, он не изменяет число, а когда умножают, превращают его в 0.
Подходят ли эти правила к нашему примеру?(нет)
Как же он поведёт себя при делении?

Сообщение темы и целей урока (слайд 8)

-Итак, какова наша цель? Решить этот пример верно.

цель

Таблица на доске.

Что для этого надо? Узнать правило деления 0 на число.

задача

— Тема нашего урока: «Деление нуля на число, невозможность деления на нуль».

— Мы рассмотрим приёмы деления нуля на число, закрепим знания таблицы умножения, умение решать составные задачи.

Усвоение новых знаний и способов действий.

Установление связи с ранее изученным.
Какие же у вас есть предположения?
0:5=0
0:5=5

предположение

Как же найти верное решение?
С каким действием связано умножение? (с делением)
Приведите пример
2 · 3 = 6
6 : 2 = 3

Можем ли мы теперь 0:5?
Это значит, надо найти число, при умножении которого на 5 получится 0.
х·5=0
Это число 0. Значит, 0:5=0.

Приведите свои примеры.

На экране: 0:6 (слайд 9)

— Подберите такое число, при умножении которого на 6 получился бы 0? (Это 0).

Значит, 0:6=0

Аналогично рассматривается случай деления 0:9.

Вывод: При делении нуля на любое другое число, получается нуль.

ПОМНИ, делить на нуль нельзя!

— Почему нельзя делить на нуль? Обоснуйте свой ответ.

(При делении на 0, например, числа 6 или другого числа, кроме нуля нельзя найти такое число, умножив которое на нуль, получилось бы 6 или другое число).

2.Послушайте сказку о нуле. (слайды 10-16)

Далеко-далеко, за морями и горами, была страна Цифрия. Жили в ней очень честные числа. Только Нуль отличался ленью и нечестностью.

Однажды все узнали, что далеко за пустыней появилась королева Арифметика, зовущая к себе на службу жителей Цифрии. Служить королеве захотели все. Между Цифрией и королевством Арифметики пролегла пустыня, которую пересекли четыре реки: Сложение, Вычитание, Умножение и Деление. Как добраться до Арифметики? Числа решили обьедениться (ведь с товарищами легче преодолевать трудности) и попробовать перейти пустыню.

Рано утром, как только солнце коснулось земли своими лучами, двинулись числа в путь. Долго шли они под палящим солнцем и, наконец, добрались до реки Сложение. Числа бросились к реке, чтобы напиться, но река сказала: «Станьте по парам и сложитесь, тогда дам вам напиться». Всё исполнили приказание реки, исполнил желание и лентяй Нуль. Но число, с которым он сложился, осталось недовольно: ведь воды река давала столько, сколько единиц было в сумме, а сумма не отличалась от числа.

Солнце еще больше печет. Дошли до реки Вычитание. Она тоже потребовала за воду плату: стать парами и вычесть меньшее число из большего, у кого ответ получится меньше, тот получит больше воды. И снова число. Стоящее в паре с Нулём оказалось в проигрыше и было расстроено.

Побрели числа дальше по знойной пустыне. Река Умножение потребовала от чисел перемножиться. Число, стоящее в паре с Нулём, вообще не получило воды. Оно еле добрело до реки Деление.

А у реки Деление никто из чисел не захотел становиться в пару с Нулём. С тех пор ни одно число не делится на нуль.

Правда, королева Арифметика примирила все числа с этим лентяем: она стала просто приписывать нуль рядом с числом, которое от этого увеличивалось в десять раз. И стали числа жить-поживать, да добра наживать.

— Сегодня мы с вами открыли ещё один фокус «нуля». Что это за «фокус»? О нём надо помнить, чтобы не допускать ошибок в вычислениях.

Первичная проверка понимания изученного. Работа по учебнику.

1.Прочитайте правило в учебнике и сравните с вашим.

А давайте попробуем любое число разделить на 0.
Например, 5:0. Сколько получится?
Нельзя подобрать такое число, при умножении которого на 0 получится 5.
Вывод: НА 0 ДЕЛИТЬ НЕЛЬЗЯ.

В каких ещё заданиях может понадобиться знание этого правила? (в решении примеров, уравнений)

Выполнения №1 стр. 75 с комментированием «цепочкой».

Физкультминутка и зарядка для глаз (слайд 17-18)

Утром стрекоза проснулась,

Потянулась, улыбнулась.

Раз — росой она умылась,

Два — изящно покружилась

Три — нагнулась и присела,

На четыре – полетела.

У реки остановилась,

Над водою закружилась.

Работа над пройденным материалом.

1)Выполнение №2 (устно)

2) Нахождение значений выражений №6 (1) стр. 85

3) Решение задачи №5 стр.85 (слайд 19)

Как вы думаете, часто ли в задачах используется число 0?
(Нет, не часто, т.к. 0 – это ничего, а в задачах должно какое-то количество чего-либо.)
Тогда будем решать задачи, где есть другие числа.
Составление таблицы на интерактивной доске.

— Прочитайте условие задачи и подумайте, как удобнее выполнить краткую запись. (В таблице).

— Какие графы должны быть в таблице?

— Что такое 8кг? (Масса 1 ящика со сливами)

Масса 1 ящика

Количество ящиков

Масса всех ящиков

Слив – 8кг

? 1) (:)

одинаковое

48 кг

Груш – 9кг

? 2) (∙)

— Что ещё известно в задаче? ( Масса 1 ящика с грушами. Масса всех ящиков со сливами.)

— Что сказано о количестве ящиков с грушами? (Их столько же). Или количество одинаковое.

-Составьте программу решения и запишите решение самостоятельно.

Б) Проверка решения.

1) 48:8=6(ящ.)

2) 9∙6=54(кг)

Ответ:54 кг груш привезли на рынок.

4)Решение уравнений с устным объяснением.

№8 стр. 85

5)Найди закономерность (задание на слайде) (слайд 20)

6)Самостоятельная работа. (слайд 21)

(Проверочная работа.с.42,43.)

Итог урока

Что нового мы узнали на уроке?
Что получится при делении нуля на любое число?
Какое важное правило должны запомнить?

Информация о домашнем задании (слайд 22)

№4, №6(2) стр. 85.

Рефлексия (см. приложение; слайды 23-24)

-Над какой темой сегодня работали? О чём вы не знали в начале урока?
-Какую цель ставили перед собой?
-Достигли вы её? С каким правилом познакомились?
— Ребята! Вам понравился урок?

— Посмотрите на «пушистиков». У них разные настроения. Раскрасьте «пушистика», у которого такое же настроение, как у вас. Покажите своих «пушистиков».( я доволен собой, у меня всё получилось ; всё хорошо, но я мог работать лучше; урок обычный, ничего интересного; ничего не получилось) Молодцы! Спасибо за урок! До новых встреч!

Урок 4 — Умножение и деление

Новый год начинается с Урока 4, Умножение и деление! Это базовые вычислительные навыки, которые дети будут часто использовать, и навыки, которыми дети должны овладеть, чтобы преуспеть в более высоких уровнях математики. Ваш ребенок разработает стратегии умножения и деления целых чисел. Они будут использовать таблицы умножения, счетчики и калькуляторы. Цели этого подразделения следующие;

1) Связать предложения с умножением с повторяющимся сложением
2) Использовать массивы для умножения и деления

3) Находить закономерности для умножения и деления на 2, на 5 и на 10
4) Изучать правила умножения и деления на 1 и на 0
5) Выводить факты умножения и деления семьи
6) Свяжите предложения деления с повторяющимся вычитанием

Важно, чтобы учащиеся поняли следующее:

В предложении умножения умножаемые числа являются ФАКТОРАМИ, а ответ называется ПРОИЗВЕДЕНИЕМ.

МАССИВ – это изображение, состоящее из точек, которые расположены в строках и столбцах. В предложении умножения первый множитель говорит о количестве строк, а второй множитель говорит о том, сколько точек в каждой строке. Массивы могут помочь показать, что изменение порядка факторов не меняет произведение.

Помните, что при умножении «раз» означает также «группы». Таким образом, хотя ответ один и тот же, 6 групп по 5 (6×5) и 5 групп по 6 (5×6) — это два разных вопроса, особенно когда их просят нарисовать картинку или определить, что изображено на ней.

При делении «делится на» также означает «разделяется на». Таким образом, 30 разделить на 5 (30 разделить на 5) отличается от 30 разделить на 6 (30 разделить на 6), и вы получите два разных ответа.

Счет без пропусков — отличный способ помочь вашему ребенку потренироваться. Как только они освоят счет с пропусками, они смогут перенести эти знания на основные факты умножения и деления.

Нажмите кнопку, чтобы перейти к игре на умножение! ———->

Игры на умножение!

Ниже приведен пример двухшаговой задачи со словами. Именно с помощью вопросов такого типа учащиеся могут показать свою способность выражать свои мысли по математике. Это то, на чем действительно сосредотачиваются ученики 3 класса, это будет важным навыком не только для EQAO, но и для всех будущих классов по математике. Мы начинаем наше объяснение со слов «Я знаю это, потому что…», а затем учащиеся должны объяснить свои мысли, ссылаясь на свои «картинки», «числа» и заканчивая своим окончательным утверждением как своими «словами»

Умножения Страгий

Трюки и советы по умножению

. ноль с любым числом не определен. Слово «деление» означает разделение чего-либо на равные части или группы таким образом, чтобы оно было разделено поровну между всеми.

Принимая во внимание, что значение нуля как числа ничто. Он ставится перед 1, это четное число, которое не является ни положительным, ни отрицательным. Давайте узнаем больше о делении на ноль и решим несколько примеров.

1.	Что такое деление на ноль?
2.	Единица, деленная на ноль
3.	Факты о делении и ноле
4.	Часто задаваемые вопросы о Division By Zero

Что такое деление на ноль?

Деление на ноль считается неопределенным, если ноль является знаменателем или делением и выражается как а/0, где а является числом, числителем или делимым. Другими словами, деление нуля на любое число всегда даст нам ноль, независимо от умножения или деления. Поскольку умножение и деление идут рука об руку, деление на ноль также может означать умножение на ноль. Например, 7/0 = x или 0 × x = 5. Здесь x не имеет значения или числа для завершения уравнения. Следовательно, деление на ноль любого числа неопределенно.

Единица, деленная на ноль

Единица, деленная на ноль, также считается неопределенной. По мнению математиков, любое ненулевое число, положительное или отрицательное, деленное на ноль, не определено, поскольку не имеет значения. Например, попробуем определить 1/0. Если мы разделим ненулевое число на небольшое положительное число, мы получим значение. Малое положительное число близко к нулю, но не равно нулю.

1/0,1 = 10, 1/0,01 = 100, 1/0,000001 = 1000000

Следовательно, когда мы делим единицу на все меньшие и меньшие положительные числа, мы получаем все большие и большие положительные числа. Следовательно, 1/0 = + бесконечность. Когда мы разделили отрицательные числа, близкие к нулю, мы получили:

1/-0,1 = -10, 1/-0,01 = -100, 1/-0,000001 = -1000000

Единица делится на отрицательное число ближе к нулю приводит к другому результату, который ближе к отрицательной бесконечности. Следовательно, 1/0 = -бесконечность. Следовательно, единица, деленная на ноль, не имеет ответа, что приводит к неопределенности.

Факты о Дивизии и Зеро

Ниже приведены некоторые факты о делении и нуле.

Любое число, деленное на 1 (частное равно делимому), дает ответ, аналогичный делимому. Другими словами, 1 — это делитель, а частное будет равно делимому. Например: 25 ÷ 1 = 25.
Число нельзя разделить на 0, поэтому результат не определен. Пример: 78 ÷ 0 = не определено (но 0 ÷ 78 = 0).
Если делимое равно делителю, что означает те же числа, но не 0, то ответ всегда равен 1. Например: 36 ÷ 36 = 1.
Ноль — это действительное число, целое число, рациональное число и целое число.
Ноль всегда нейтрален, т. е. ноль никогда не записывается как +0 или -0.
Степень любого числа, увеличенного на ноль, всегда равна единице.

Связанные темы

Ниже перечислены несколько интересных тем, связанных с делением на ноль. Смотри:

Длинная часть
Нулевое свойство умножения
Дивизион Формула
Деление дробей

Примеры деления на ноль

Пример 1: Если в офисе есть 7 ягод клубники, а в офисе никого нет, сколько клубники получит каждый в офисе?
Решение: Дано, 7 клубник в офисе и никого вокруг. Раздавать клубнику, когда никого нет в офисе, заведомо невозможно. Кому достанется клубника? Это определенно не имеет никакого смысла, поэтому this не определено.
Пример 2: Что такое 0 ÷ 7?
Решение: Ноль, разделенный на любое действительное число, кроме 0, равен нулю. Следовательно, 0 ÷ 7 = 0,

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатное пробное занятие

Практические вопросы по разделу на ноль