Умножение и деление на 0 3 класс: Умножение и деление 0 — урок. Математика, 3 класс.

а, а : 1, 0 : а

Этап усвоения новых знаний

 

Ребята, вспомните, что такое умножение?
Умножение – это сложение одинаковых слагаемых
 

Замените в следующих примерах произведение суммой и запишите.

5 · 3 =
5 · 2=
5 · 1=

Проверьте себя.

5 · 3 = 5 + 5 + 5 + 5
5 · 2 = 5 + 5    
5 · 1 = ?
5 · 0 = ?
 

Удалось ли заменить сложением последние два примера?
Это особые случаи.
Нельзя взять число слагаемым один раз. Поэтому применим переместительное свойство умножения:
1 · 5 = 1 + 1 + 1 + 1 + 1 = 5

 

Кроме табличных случаев умножения и деления в математике, существуют случаи, которые называют особыми — это

математические законы, которые нужно знать: при умножении любого числа на 1, получается то число, которое умножали.   
     

В математике обозначают любое число латинской буквой а.
Запишите этот вывод формулой.
а · 1 = а
 

Запомните!
Вместо буквы а мы можем подставить любое число.
 

Рассмотрим подробно пример 5 · 0 = ?
К данному случаю можно применить переместительное свойство умножения.
0 · 5 = 0 + 0 + 0 + 0 + 0 = 0

 

Второй математический закон, который нужно сегодня запомнить:
Произведение считается равным нулю, при умножении на 0.
 

Запишите этот вывод формулой.

а · 0 = 0
 

Запомните!
Вместо буквы а,  мы можем подставить любое число.
 

Лучшему запоминанию новых случаев умножения будет способствовать создание наглядного образа.

Множитель 1 не изменяет число, его можно представить зеркальцем.
Как бы отражает второй множитель, не изменяя его.

Нуль – это шапка – невидимка. Он при умножении покрывает второй множитель и делает его невидимым.

Давайте вспомним, что такое деление.
Деление — это действие, обратное умножению.
Каждому примеру на умножение можно составить два обратных примера на деление.
Рассмотрим подробно следующие случаи деления:

а : а = ?
а : 1 = ?
0 : а = ?
 

Запишите пример 5 · 1 = ?
Проверим 5 · 1 = 5

Каждому примеру на умножение можно составить два обратных примера на деление. 
Составим и запишем.

5 : 5 = ?
Проверим 5 : 5=1

Делаем вывод:
При делении числа на то же самое число получается единица. Запишем буквенное выражение или формулу

а : а = 1
ЗАПОМНИТЕ!

 

Запишем второй пример на деление.
 5 : 1 = ?

Проверим
5 : 1 = 5

Делаем вывод:
При делении числа на 1 получается то же самое число
Запишем буквенное выражение или формулу
а : 1 = а          

      

Решим ещё один пример на деление, запишите
0 : 5 = ?….
Это значит, надо найти число, при умножении которого на 5 получится 0.
х · 5 = 0

Это будет число 0. Значит, 0 : 5 = 0…..

Делаем вывод:
При делении 0 на любое число получается 0.
Запишем буквенное выражение или формулу
0 : а = 0

 

Этап закрепления новых знаний

 

Задание 1

Выполните вычисления.

91 ∙ 1 =
64 + 0 =
18 ∙ 0 =
1 ∙ 35 =
25 + 1 =
0 ∙ 361 =
72 ∙ 0 =
54 ∙ 1 =
31 — 0 =
0 ∙ 159 =
1 ∙ 76 =
98 — 1 =

Проверьте себя и оцените свои успехи.

91 ∙ 1 = 91
64 + 0 = 64
18 ∙ 0 = 0
1 ∙ 35 = 35
25 + 1 = 26
0 ∙ 361 = 0
72 ∙ 0 = 0
54 ∙ 1 = 54
31 — 0 = 31
0 ∙ 159 = 0
1 ∙ 76 = 76
98 — 1 = 97
 

Задание 2

Найдите числовые выражения, при решении которых допущена ошибка. Запишите эти выражения, сделав вычисления правильно.

1 · 15 = 15
3 · 0 = 3
19 : 19 = 1
23 : 1 = 1

26 : 26 = 1
12 + 0 = 0
17 — 0 = 17

Проверьте себя и оцените свои успехи.

3 · 0 = 0
23 : 1 = 23
12 + 0 = 12

 

Этап подведения итогов

 

Давайте повторим:

1. При умножении любого числа на 1 получается число, которое умножаем.
2. При умножении любого числа на 0 получается 0.
3. При делении числа на то же самое число получается единица.
4. При делении числа на 1 получается то же самое число.
5. При делении 0 на любое число получается 0.
   
    

Запомните! Делить на нуль нельзя!

 

Рефлексия

 

Выберите смайлик, который более всего соответствует вашему пониманию изученных сегодня на уроке правил и нарисуйте его у себя в тетради.

Спасибо за работу, вы хорошо потрудились!       

Урок математики в 3 классе. Тема урока: «Деление 0 на число. Невозможность деления на 0». | План-конспект урока по математике (3 класс) по теме:

                                   Учебник: «Математика» 3 класс  М.И. Моро

Цели урока: создать условия для формирования умения делить 0 на число.

Задачи урока:

• раскрыть смысл деления 0 на число через связь умножения и деления;
• развивать самостоятельность, внимание, мышление;
• формировать навыки решения примеров на табличное умножение и деление.

Для достижения цели урок был разработан с учётом деятельностного подхода.

Структура урока включала в себя:

1. Орг. момент, целью которого было позитивно настроить детей на учебную деятельность.
2. Мотивация позволила актуализировать знания, сформировать цели и задачи урока. Для этого были предложены задания на нахождение лишнего числа, классификацию примеров на группы, добавление недостающих чисел. В ходе решения этих заданий, дети столкнулись спроблемой: нашёлся пример, для решения которого не хватает имеющихся знаний. В связи с этим дети самостоятельно сформулировали цель и поставили перед собой учебные задачи урока.
3. Поиск и открытие нового знания дал возможность детям предложить различные варианты решения задания. Основываясь на ранее изученный материал, они смогли найти верное решение и прийти к выводу, в котором сформулировали новое правило.
4. Во время первичного закрепления ученики комментировали свои действия,работая по правилу, дополнительно были подобраны свои примеры на это правило.
5. Для автоматизации действий и умения пользоваться правилам в нестандартных заданиях дети решали уравнения, выражения в несколько действий.
6. Самостоятельная работа и проведенная взаимопроверка показали, что большинство детей тему усвоили.
7. Во время рефлексии дети сделали вывод, что поставленная цель урока достигнута и оценили себя с помощью карточек.

В основе урока лежали самостоятельные действия учащихся на каждом этапе, полное погружение в учебную задачу. Этому способствовали такие приёмы, как работа в группах, само- и взаимопроверка, создание ситуации успеха, дифференцированные задания, саморефлексия.

Урок математики в 3 классе.

Тема урока: «Деление 0 на число. Невозможность деления на 0»

Цели урока: создать условия для формирования умения делить 0 на число.

Задачи урока:

• раскрыть смысл деления 0 на число через связь умножения и деления;
• развивать самостоятельность, внимание, мышление;
• формировать навыки решения примеров на табличное умножение и деление.

                                                   Ход урока.

1. Организационный этап.

 Проверьте свою готовность к уроку, сядьте прямо.
Потрите свои ушки, чтобы кровь активнее поступала в мозг. Сегодня у вас будет много интересной работы, с которой, я уверена, вы справитесь на отлично.

2.  (слайд 1; 2; 3)

                   Веселый прозвенел звонок,

Мы начинаем наш урок.

Все ли правильно сидят,

                Все внимательно глядят?

                Каждый хочет получать

                Только лишь оценку пять!

— Откройте свои тетради, запишите сегодняшнее число. (слайд 4) Что вы можете сказать о числе 20? (Оно двузначное; оно чётное; состоит из разряда десятков и разряда единиц).

— Сколько десятков и сколько единиц в нём? (2 десятка и 0 единиц.).

3. Устный счёт.

1. Игра «Найди лишнее число»  (слайд 5)

-Из каждого столбика выберите «лишнее число»

6 18 24 22 30

23 28 16 26 24

66 88 77 55 13

---

2. Найдите площади фигур: (слайд 6)

3.Арифметический диктант:

1. Какое число надо умножить на 7, чтобы получить 42?
2. Назовите число, которое меньше 24 на 6?
3. Из какого числа надо вычесть 18, чтобы получить 3?
4. Во сколько раз 4 десятка больше 5?
5. Найдите произведение 9 и 3.
6. Делимое 36, частное 6. Чему равен делитель?
7. Увеличьте 8 в 6 раз.
8. На какое число надо разделить 28, чтобы получить 7?

— Запишите только ответы.

(Взаимопроверка: 6, 18, 21, 8, 27, 6, 48, 4.) – (слайд 7)

4.Индивидуальная работа  (работа по карточкам, см. приложения)

5. Создание проблемной ситуации
Задания в парах:
— расставьте примеры в 2 группы:

Почему так распределили? (с ответом 4 и 5)

— решите примеры:
8·7-6+30:6=
28:(16:4)·6=
30-(20-10:2):5=
30-(20-10·2):5=

— Что вы заметили? Есть ли здесь лишние примеры?
— Все ли примеры вы смогли решить?
— У кого возникли затруднения?
— Чем этот пример отличается от остальных?
— Если кто-то решил, то молодец. Но почему не все смогли справиться с этим примером?

6.Постановка учебной задачи.
Здесь есть пример с 0. А от 0 можно ожидать разные фокусы. Это необычное число.
Вспомните, что вы знаете про 0? (а·0=0, 0·а=0, 0+а=а)·
Приведите примеры.
Посмотрите, какой он коварный: когда его прибавляют, он не изменяет число, а когда умножают, превращают его в 0.
Подходят ли эти правила к нашему примеру?(нет)
Как же он поведёт себя при делении?

4. Сообщение темы и целей урока  (слайд 8)

-Итак, какова наша цель? Решить этот пример верно.

цель

Таблица на доске.

Что для этого надо?  Узнать правило деления 0 на число.

задача

— Тема нашего урока: «Деление нуля на число, невозможность деления на нуль».

— Мы рассмотрим приёмы деления нуля на число, закрепим знания  таблицы умножения, умение решать составные задачи.

5. Усвоение новых знаний и способов действий.

Установление связи с ранее изученным. Какие же у вас есть предположения? 0:5=0 0:5=5 предположение

Как же найти верное решение? С каким действием связано умножение? (с делением) Приведите пример 2 · 3 = 6 6 : 2 = 3 Можем ли мы теперь 0:5? Это значит, надо найти число, при умножении которого на 5 получится 0. х·5=0 Это число 0. Значит, 0:5=0. Приведите свои примеры.

1. На экране: 0:6   (слайд 9)

— Подберите такое число, при умножении которого на 6 получился бы 0? (Это 0).

Значит, 0:6=0

   Аналогично рассматривается случай деления 0:9.

Вывод: При делении нуля на любое другое число, получается нуль.

ПОМНИ, делить на нуль нельзя!

— Почему нельзя делить на нуль? Обоснуйте свой ответ.

(При делении на 0, например, числа 6 или другого числа, кроме нуля нельзя найти такое число, умножив которое на нуль, получилось бы 6 или другое число).

 2.Послушайте сказку о нуле. (слайды 10-16)

Далеко-далеко, за морями и горами, была страна Цифрия. Жили в ней очень честные числа. Только Нуль отличался ленью и нечестностью.

Однажды все узнали, что далеко за пустыней появилась королева Арифметика, зовущая к себе на службу жителей Цифрии. Служить королеве захотели все. Между Цифрией и королевством Арифметики пролегла пустыня, которую пересекли четыре реки: Сложение, Вычитание, Умножение и Деление. Как добраться до Арифметики? Числа решили обьедениться (ведь с товарищами легче преодолевать трудности) и попробовать перейти пустыню. 

Рано утром, как только солнце коснулось земли своими лучами, двинулись числа в путь. Долго шли они под палящим солнцем и, наконец, добрались до реки Сложение. Числа бросились к реке, чтобы напиться, но река сказала: «Станьте по парам и сложитесь, тогда дам вам напиться». Всё исполнили приказание реки, исполнил желание и лентяй Нуль. Но число, с которым он сложился, осталось недовольно: ведь воды река давала столько, сколько единиц было в сумме, а сумма не отличалась от числа.                        

Солнце еще больше печет. Дошли до реки Вычитание. Она тоже потребовала за воду плату: стать парами и вычесть меньшее число из большего, у кого ответ получится меньше, тот получит больше воды. И снова число. Стоящее в паре с Нулём оказалось в проигрыше и было расстроено.

Побрели числа дальше по знойной пустыне. Река Умножение потребовала от чисел перемножиться. Число, стоящее в паре с Нулём, вообще не получило воды. Оно еле добрело до реки Деление.

А у реки Деление никто из чисел не захотел становиться в пару с Нулём. С тех пор ни одно число не делится на нуль.

Правда, королева Арифметика примирила все числа с этим лентяем: она стала просто приписывать нуль рядом с числом, которое от этого увеличивалось в десять раз. И стали числа жить-поживать, да добра наживать.

— Сегодня мы с вами открыли ещё один фокус «нуля». Что это за «фокус»? О нём надо помнить, чтобы не допускать ошибок в вычислениях.

6. Первичная проверка понимания изученного. Работа по учебнику.

1.Прочитайте правило в учебнике и сравните с вашим.

А давайте попробуем любое число разделить на 0.
Например, 5:0. Сколько получится?
Нельзя подобрать такое число, при умножении которого на 0 получится 5.
Вывод: НА 0 ДЕЛИТЬ НЕЛЬЗЯ.

В каких ещё заданиях может понадобиться знание этого правила? (в решении примеров, уравнений)

2. Выполнения №1 стр. 75 с комментированием «цепочкой».

Физкультминутка и зарядка для глаз (слайд 17-18) 

Утром стрекоза проснулась,

Потянулась, улыбнулась.

Раз — росой она умылась,

Два — изящно покружилась

Три — нагнулась и присела,

На четыре – полетела.

У реки остановилась,

Над  водою закружилась.

7. Работа над пройденным материалом.

1)Выполнение №2 (устно)

    2)  Нахождение значений выражений №6 (1) стр. 85

    3) Решение задачи №5 стр.85  (слайд 19)

Как вы думаете, часто ли в задачах используется число 0?
(Нет, не часто, т.к. 0 – это ничего, а в задачах должно какое-то количество чего-либо.)
Тогда будем решать задачи, где есть другие числа.
Составление таблицы на интерактивной доске.

—  Прочитайте условие задачи и подумайте, как удобнее выполнить краткую запись. (В таблице).

— Какие графы должны быть в таблице?

— Что такое 8кг? (Масса 1 ящика со сливами)

Масса 1 ящика	Количество ящиков	Масса всех ящиков
Слив  – 8кг	?   1) (:) одинаковое	48 кг
Груш – 9кг		?   2) (∙)

 — Что ещё известно в задаче? ( Масса 1 ящика с грушами.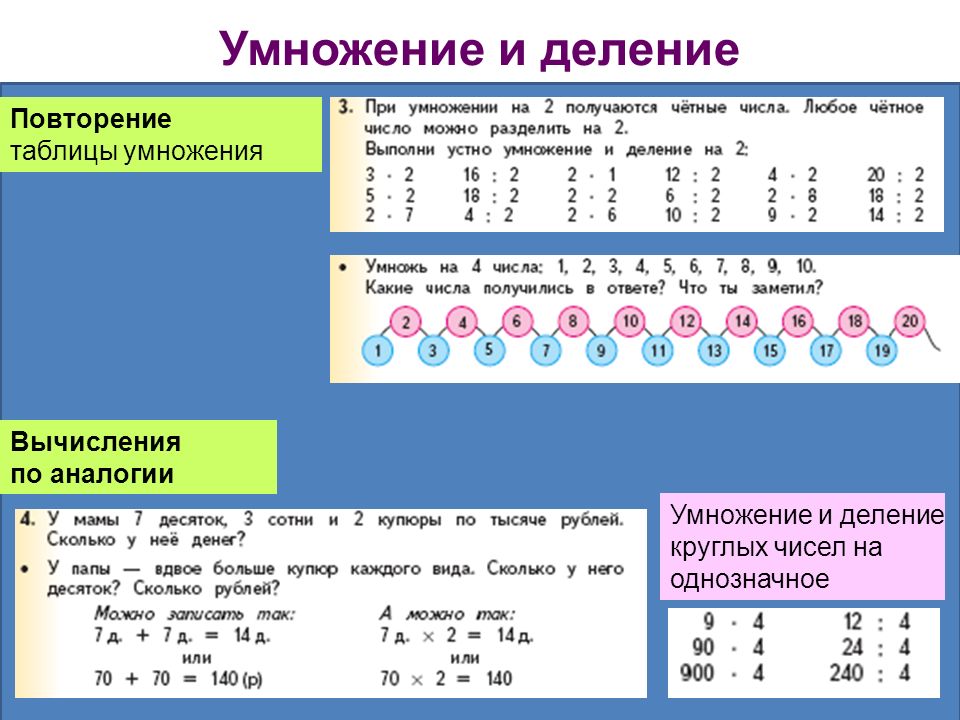 Масса всех ящиков со сливами.)

— Что сказано о количестве ящиков с грушами?  (Их столько же). Или количество одинаковое.

-Составьте программу решения и запишите решение самостоятельно.

Б) Проверка решения.

1) 48:8=6(ящ.)

2) 9∙6=54(кг)

Ответ:54 кг груш привезли на рынок.

   4)Решение уравнений с устным объяснением.

№8 стр. 85

   5)Найди закономерность (задание на слайде) (слайд 20)

    6)Самостоятельная работа. (слайд 21)

 (Проверочная работа.с.42,43.)

8. Итог урока

• Что нового мы узнали на уроке?
• Что получится при делении нуля на любое число?
• Какое важное правило должны запомнить?

9. Информация о домашнем задании  (слайд 22)

№4, №6(2) стр. 85.

       Рефлексия  (см. приложение; слайды 23-24) 

-Над какой темой сегодня работали? О чём вы не знали в начале урока?
-Какую цель ставили перед собой?
-Достигли вы её? С каким правилом познакомились?
— Ребята! Вам понравился урок?

— Посмотрите на «пушистиков». У них разные настроения. Раскрасьте «пушистика», у которого  такое же  настроение, как у вас. Покажите своих «пушистиков».( я доволен собой, у меня всё получилось ;  всё хорошо, но я мог работать лучше; урок обычный, ничего интересного; ничего не получилось)  Молодцы! Спасибо за урок! До новых встреч!

Урок 4 — Умножение и деление

Новый год начинается с Урока 4, Умножение и деление! Это базовые вычислительные навыки, которые дети будут часто использовать, и навыки, которыми дети должны овладеть, чтобы преуспеть в более высоких уровнях математики. Ваш ребенок разработает стратегии умножения и деления целых чисел. Они будут использовать таблицы умножения, счетчики и калькуляторы. Цели этого подразделения следующие;

1) Связать предложения с умножением с повторяющимся сложением
2) Использовать массивы для умножения и деления 
3) Находить закономерности для умножения и деления на 2, на 5 и на 10
4) Изучать правила умножения и деления на 1 и на 0 
5) Выводить факты умножения и деления семьи
6) Свяжите предложения деления с повторяющимся вычитанием

Важно, чтобы учащиеся поняли следующее:

В предложении умножения умножаемые числа являются ФАКТОРАМИ, а ответ называется ПРОИЗВЕДЕНИЕМ.

МАССИВ – это изображение, состоящее из точек, которые расположены в строках и столбцах. В предложении умножения первый множитель говорит о количестве строк, а второй множитель говорит о том, сколько точек в каждой строке. Массивы могут помочь показать, что изменение порядка факторов не меняет произведение.

Помните, что при умножении «раз» означает также «группы». Таким образом, несмотря на то, что ответ один и тот же, 6 групп по 5 (6×5) и 5 ​​групп по 6 (5×6) — это два разных вопроса, особенно когда их просят нарисовать картинку или определить, что изображено на ней.

При делении «делится на» также означает «разделяется на». Таким образом, 30 разделить на 5 (30 разделить на 5) отличается от 30 разделить на 6 (30 разделить на 6), и вы получите два разных ответа.

Счет без пропусков — отличный способ помочь вашему ребенку потренироваться. Как только они освоят счет с пропусками, они смогут перенести эти знания на основные факты умножения и деления.

Нажмите кнопку, чтобы перейти к игре на умножение! ———->

Игры на умножение!

Ниже приведен пример двухшаговой задачи со словами.

Именно с помощью вопросов такого типа учащиеся могут показать свою способность выражать свои мысли по математике. Это то, на чем действительно сосредотачиваются ученики 3 класса, это будет важным навыком не только для EQAO, но и для всех будущих классов по математике. Мы начинаем наше объяснение со слов «Я знаю это, потому что…», а затем учащиеся должны объяснить свои мысли, ссылаясь на свои «картинки», «числа» и заканчивая своим окончательным утверждением как своими «словами»

Умножения Стигений

Трюки и советы по умножению

. второго, третьего и четвертого классов. Им нужно запомнить много фактов, и некоторым детям будет трудно понять концепции. Вы можете использовать различные стратегии, описанные в этом посте (от конкретных до абстрактных), чтобы сделать умножение и деление забавным, а не рутиной. Как родитель, обучающийся на дому, вы можете выбирать, какая стратегия умножения или деления лучше всего подходит для вашего ребенка начального возраста.

Умножение и деление

Умножение и деление — две из четырех основных математических операций. Один складывает или умножает одно и то же число заданное количество раз, а другой показывает, сколько раз одно число входит в другое число. Без четкого понимания этих операций ребенок не сможет преуспеть в более сложных математических исследованиях. Дети, которым не удается усвоить факты умножения однозначных цифр, будут отставать от своих сверстников в средней и старшей школе.

В каком классе вы изучаете умножение? Большинство детей начинают изучать умножение во втором классе.

В каком классе ты изучаешь дивизию? Дети часто начинают изучать деление во втором или третьем классе.

В каком классе вы изучаете деление в длинной стрелке? Дети изучают дробь в третьем или четвертом классе.

Как связаны умножение и деление?

Умножение и деление являются обратными операциями. То есть одно отменяет другое. Каждое уравнение умножения имеет связанное с ним уравнение деления, использующее те же три числа. При умножении вы умножаете два множителя, чтобы получить произведение. При делении вы начинаете с произведения (дивиденда) и делите на один множитель (делитель), в результате чего получается другой множитель (частное).

Как проверить деление с помощью умножения

Поскольку умножение и деление являются обратными операциями, вы можете проверить результат деления, перемножив частное и делитель, чтобы получить делимое. Например, если вы получили 3 при ответе на 21, деленное на 7, вы можете проверить свой ответ, умножив 7 на 3.

Ключевые понятия перед изучением умножения и деления

переходим к умножению. Например, ученик должен знать, что семь — это то же самое, что один плюс шесть, два плюс пять или три плюс четыре. Коммутативное свойство сложения (свойство, которое позволяет вам инвертировать числа, которые вы складываете вместе, и получать тот же результат, например, 3+4=7 и 4+3=7) также применимо к умножению. Знакомство с использованием числовой строки для сложения поможет, когда придет время многократно складывать одно и то же число.

Как учить умножению и делению

Обучение умножению и делению следует начинать с конкретных методов, прежде чем переходить к абстрактным уравнениям. Дети начальных классов получат наибольшее понимание, работая с манипуляторами и реальными проблемами для начала. В классе учитель будет использовать большинство из этих стратегий для учета способностей учащихся к обучению, но как родитель, обучающийся на дому, вы можете выбирать, какие из них лучше всего подходят для ваших детей. Ваша цель для ваших детей должна заключаться в том, чтобы понять и уметь применять умножение и деление, чтобы они могли использовать их по мере перехода к более сложным понятиям.

Стратегии и методы умножения

Здесь представлены различные стратегии обучения умножению, которые развиваются от конкретного к абстрактному.

1. Умножение с помощью манипуляторов

Для начала дети должны научиться умножению, составляя группы элементов. Вы можете подарить им маленькие кубики Unifix, монеты или любой другой предмет, который у вас есть. Идея состоит в том, что они создадут несколько групп одинакового размера, а затем смогут физически подсчитать все объекты.

2. Умножение с помощью числовой строки

Поскольку умножение представляет собой многократное сложение, дети, знакомые со сложением в числовой строке, смогут складывать одно и то же число снова и снова, чтобы получить результат умножения. Перейдите к использованию повторного сложения без конкретной числовой строки.

3. Используйте модель массива

Если вы использовали маленькие кубики, такие как кубики Unifix, в качестве манипуляции для обучения умножению, переход к массивам будет плавным. Расположите кубы в прямоугольные массивы, каждая сторона которых имеет длину, заданную коэффициентами в вашей задаче на умножение. Например, число 12 представляет собой прямоугольный массив из трех блоков по четыре блока или двух блоков по шесть блоков. Эта модель также работает как первое знакомство с нахождением площади прямоугольника или подобной формы.

4. Используйте таблицу умножения

Таблица умножения – удобный инструмент для детей, пока они не выучат таблицу умножения на однозначные числа. Он имеет числа от 0 до 9 внизу слева и вверху (многие таблицы могут содержать только числа от 1 до 9 или доходить до 12). На пересечении каждой строки и столбца находится произведение числа слева и сверху. Дети должны уметь распознавать закономерности в таблице, что поможет им в изучении фактов умножения.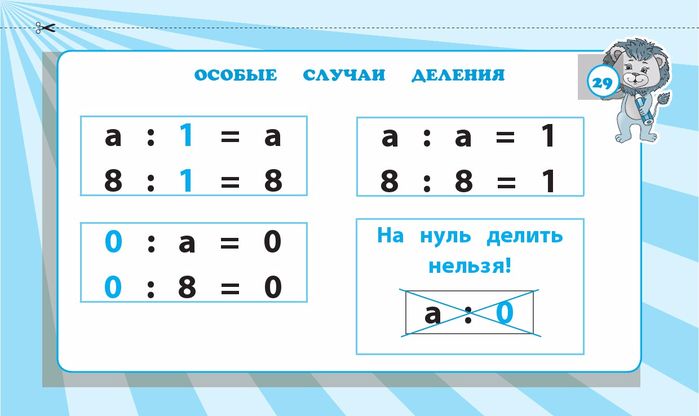 Например, все продукты девятой строки имеют цифры, которые в сумме дают девять (кроме 0 x 9).). Дети легко начнут изучать переместительное свойство умножения, заметив, что произведение на пересечении двух чисел одинаково, независимо от того, начинаете ли вы слева или сверху.

5. Пропустите счет, чтобы умножить

Детям обычно нравится скорость и сложность счета пятерками или десятками. Счет со пропуском проведет вас через все числа, кратные числу, когда вы идете. Попробуйте считать тройками или семерками, чтобы помочь детям попрактиковаться в запоминании фактов умножения. Вы можете начать с использования таблицы умножения, выбора строки и подсчета всех продуктов в этой строке. При достаточной практике дети должны начать запоминать эти факты умножения.

6. Запомните факты об умножении однозначных чисел

После того, как вы полностью изучите концепцию умножения и то, как и почему оно работает, часто рекомендуется, чтобы дети запоминали факты умножения от нуля до девяти. Эти однозначные факты имеют решающее значение для возможности решения многозначного умножения в будущем. Если дети не усвоят эти факты, они могут быть не готовы перейти к дробям, а затем начать изучать алгебру. Карточки могут быть полезны, когда дети запоминают эти факты.

7. Использование коммутативных и дистрибутивных свойств

Три свойства помогут детям понять умножение и даже помогут им придумывать трюки. Свойство коммутативности говорит о том, что два числа можно умножать в любом порядке. а х б = б х а. Как только ребенок выучил факты о нулях и единицах, он уже будет знать первые два факта всех остальных таблиц умножения. Распределительное свойство говорит о том, что умножение числа на два слагаемых и сложение их вместе равносильно умножению числа на их сумму. а х (b + с) = (а х b) + (а х с). Используя это свойство, дети, которые знают пять фактов и два факта, могут найти семь фактов, умножив каждое число на 5 и на 2, а затем сложив их вместе. Например, 7 х 6 = 5 х 6 + 2 х 6 = 30 + 12 = 42,9. 0011

Стратегии и методы разделения

1. Разделение с помощью манипуляторов

Дайте детям несколько манипуляторов или предметов и попросите их разделить их на равные группы. Начните с простых текстовых задач, например: «Если вы хотите разделить девять яблок поровну между тремя друзьями, сколько яблок достанется каждому другу?» Концепция равного распределения является основой разделения.

2. Использование модели измерения в сравнении с разделительной моделью деления

В партитивной (части целого) модели деления ребенок разделит счетчики (манипуляторы, используемые для счета) равномерно на определенное количество групп ( делитель) по принципу «один для вас и один для меня», а затем посчитайте окончательную сумму в одной группе, чтобы получить ответ. В модели измерения ребенок начнет составлять наборы из определенного числа (делителя), а количество наборов, которое у него будет в конце, будет ответом. Полезно предлагать детям решать задачи на деление обоими способами, чтобы физически продемонстрировать, что они получат одинаковый результат.

3. Деление в числовой строке

Деление выглядит как многократное вычитание в числовой строке. Ребенок должен начать с делимого и делать каждый прыжок назад по числовой прямой на величину делителя. Количество прыжков будет частным. Этот процесс также известен как чанкинг. Как только дети будут уверенно пользоваться числовой линией, вы можете перейти к повторному вычитанию без конкретной числовой строки.

4. Модель массива деления

Как и в модели массива умножения, маленькие кубики хорошо подходят для обучения делению. Например, дайте детям 12 кубиков и попросите их составить прямоугольники с ровными рядами. Сначала они могут попытаться построить ряды по пять штук и обнаружить, что остались блоки. Ряды 2, 3, 4 или 6 будут работать как раз и дадут вам все множители 12.

5. Модель номера отдела

Модель номера раздела использует факты умножения, которые ребенок выучил, чтобы получить ответы. Дети могут вытащить таблицу умножения и найти делимое в таблице в столбце или строке, соответствующей делителю.

Лучший способ научить умножению и делению в домашней школе

Лучший способ научить умножению и делению — это пройти через несколько стратегий от конкретного к абстрактному. Начните с того, что дайте детям манипуляторы для работы. Объединение объектов в равные группы создает физическую связь между умножением и делением. В конце концов, дети должны иметь достаточное понимание концепций, чтобы они могли решить уравнение, которое является более абстрактным. Только после того, как дети поймут концепцию умножения, они должны начать запоминать факты умножения одной цифры. Многие учебные программы настоятельно рекомендуют или требуют запоминания таблицы умножения от 0 до 12 или от 1 до 9.. Если у ваших детей проблемы с запоминанием, дайте им побольше практики с математическими фактами. Знакомство с математическими фактами, по крайней мере, с числами от 0 до 9, будет иметь решающее значение для многозначного умножения и длинного деления. В AfterSchoolHelp доступны упражнения на скорость для дополнительной практики с умножением и делением.

Как преподавать умножение и деление в классах

Преподавание деления и умножения во 2-м классе

Во втором классе обучайте умножению с помощью очень конкретных стратегий. Если дети не прогрессируют в запоминании фактов, у них все равно будет прочная основа для третьего класса. Начните вводить деление как концепцию распределения равных сумм между группами.

Обучение делению и умножению в 3-м классе

В третьем классе снова начните с конкретных примеров и текстовых задач. Массивы и подсчет пропусков полезны и в третьем классе. Дети должны продолжить работу с фактами умножения. Вы также можете ввести идею области с массивами. Дайте третьеклассникам конкретную практику деления, например, разделите пиццу на 12 кусков поровну между 4 членами семьи.

Преподавание деления и умножения в 4 классе

Продолжайте использовать конкретные манипуляторы разных цветов для представления разных значений места. Используйте много картинок и реальных жизненных задач. По мере того, как они умножают и делят многозначные числа, раздайте им миллиметровую бумагу, чтобы дети были организованы. Визуализируйте проблемы, когда это возможно.

Как преподавать деление в длинное число

Обучение делению в длинное деление в виде последовательности шагов: деление, умножение, вычитание и выпадение остатка. Начните с деления чисел, у которых нет остатка ни на одном шаге, например, 84, разделенных на 2. Без остатка, о котором нужно беспокоиться, процесс упрощается. Затем на последнем шаге используйте задачи с остатком, например 85 разделить на 2. Наконец, переходите к задачам с остатком в десятках, например 9.6 разделить на 4 или в одном или в обоих местах. Подчеркните, что этапы умножения и вычитания заключаются в поиске остатка для переноса на следующее место.

Обучение умножению и делению детей с особыми потребностями

Обучение умножению и делению детей с особыми потребностями ничем не отличается от описанных выше стратегий. Во многих случаях этим детям потребуется более длительный период на конкретной стадии обучения, прежде чем они перейдут к более абстрактным методам. Миллиметровая бумага может быть полезна для детей, чтобы упорядочить числа. Его также можно использовать для рисования массивов при изучении умножения и деления. Описанный выше трюк с распределительным свойством может быть особенно полезен детям, у которых проблемы с запоминанием, позволяя им запоминать меньше фактов, но при этом находить ответы на более сложные вопросы.

Увлекательные способы обучения умножению и делению

• Дайте детям конфеты или закусочные манипуляторы, которые они могут съесть после тренировки умножения или деления.
• Используйте пронумерованные карты, чтобы играть в такую ​​игру, как ловить рыбу, только вместо того, чтобы выкладывать пары, выкладывайте числа так, чтобы одно делилось на другое поровну. Вы можете обнаружить, что все ищут этих тузов.
• Бросьте пару игральных костей и напишите уравнения умножения и деления, используя эти два числа. Например, вы выбрасываете 3 и 4 и пишете 3 x 4 = 12, 4 x 3 = 12, 12 ÷ 4 = 3, 12 ÷ 3 = 4.
• Поиграйте с детьми в видео- или настольные игры, в которых используются цифры.
• Познакомьте детей младшего возраста с математическими понятиями с помощью образовательных шоу. Недавно моя четырехлетняя дочь продемонстрировала свое обучение на шоу, когда готовила хот-доги со своей бабушкой. Когда бабушка спросила ее, сколько, по ее мнению, она съест. Она разделила в уме восемь на два и сказала: «У нас восемь хот-догов, так что ты можешь съесть четыре, а я могу съесть четыре».

Подход BJU Press к умножению и делению

Подход BJU Press к обучению умножению и делению всегда был основан на манипулятивном подходе. Мы поощряем использование манипуляций во всех наших математических программах и предоставляем манипулятивные пакеты для математики с K5 по математику 4. Наша программа предназначена для того, чтобы познакомить учащихся с математическими понятиями с помощью физических манипуляций, прежде чем переходить к рабочим уравнениям.

• Приобретите нашу учебную программу по математике 2.