Конспект урока «Умножение на однозначное число столбиком»
Конспект урока по математике на тему:
Тема: «Умножение на однозначное число столбиком»
Предмет: математика (ПНШ)
Класс: 3 класс
Авторы урока: Морозова А.С. (учитель начальных классов).
Образовательное учреждение: МОУ «Средняя школа №10»
Тема: «Умножение на однозначное число столбиком»
Цель урока: научиться умножать многозначное число на однозначное столбиком.
Задачи урока:
образовательные: сформулировать алгоритм умножения многозначного числа на однозначное столбиком.
развивающие: развивать логическое и алгоритмическое мышление, память, математическую речь.
воспитательные: воспитывать самостоятельность, уважительное отношение к мнению одноклассников.
Планируемые результаты урока:
Предметные — знать алгоритм умножения многозначного числа на однозначное столбиком.
Метапредметные:
Познавательные — построение речевого высказывания в устной и письменной форме; сравнение, анализ и синтез, установление причинно-следственных связей.
Регулятивные — принятие и сохранение учебной задачи; осуществление контроля и оценки по эталону, рефлексивная самооценка;
Коммуникативные — формулирование вопросов и своих затруднений; построение монологических и диалогических высказываний; работа в парах;
Личностные — внутренняя позиция школьника на уровне положительного отношения к школе; учебно — познавательный интерес к новому учебному материалу.
Ход урока.
1. Актуализация знаний.
Начнем наш урок с устного счета.
Назовите число, в котором:
— 3 сотни 5 десятков и 6 единиц (356)
— 4 сотни 2 десятка и 8 единиц (428)
— 2 тысячи 8 сотен 4 десятка и 3 единицы (2843)
Задачи-шутки на сообразительность
— У Сени 7 пар носков. Сколько носков на правую ногу? (7)
— У мамы семь сыновей. У каждого сына есть родная сестра. Сколько у мамы детей? (8)
— В 11 часов малыш проснулся. Когда он лег спать, если проспал 2 часа? (9)
— Наступил декабрь. Распустились 3 ромашки, а потом еще 1. Сколько цветов распустилось? (0)
Найдите значения выражения
6*8 9*40 3*6
500*3 600*8 217*3
— Хорошо, молодцы! Значение какого произведения было труднее всего найти? (217*3)
— Почему? Это табличный случай умножения? (трёхзначное число это не табличный способ)
2. Постановка учебной задачи.
Постановка учебной задачи.
-Откройте учебник на стр.7 прочитайте тему урока, сформулируйте цель урока.
(Научиться умножать многозначное число на однозначное столбиком)
3. Объяснение нового материала.
1) Учебник №1, стр. 7
-Прочитайте задание. Правильно выполнено умножение? (да)
(2 ученика у доски)
Без перехода через разряд | Переход через разряд | |||||
23 *3 69 | 221 *4 884 | 34 *2 68 | 26 *3 78 | 47 *2 94 | 156 *2 312 | |
Обратите внимание, под каким разрядом мы записываем второй множитель.
(под разрядом единиц первого множителя)
2) Учебник № 2, с.7
-Мы решали похожие примеры?
-Сейчас, мы подробно разберем, как умножать на однозначное число.
(учитель объясняет алгоритм решения примера умножения на однозначное число, используя вопросы задания)
2 273 * 3 819 | 1) Какое число получается при умножении числа в разряде единиц? (9) 2) Можно ли его сразу записать в разряд единиц конечного результата?! (Да) 3) Какое число получается при умножении в разряде десятков? (21) 4) Сколько в 21 десятке содержится сотен и сколько еще десятков? (21 дес. = 210 единиц; 210 = 2 сот. 5) Какую цифру мы записываем в разряд десятков результата? (1) 6) В какой разряд переходят 2 сотни? (в сотни) 7) Какое число получается при умножении в разряде сотен? (6) 8) Сколько сотен перешло в этот разряд при выполнении умножения в предыдущем разряде? (2) 9) Сколько всего сотен получилось с учетом перехода? (8) 10) Какую цифру нужно записать в разряд сотен результата9 (8) 11) Назовите значение произведения ? (819) 12) Ре6ята читают сами. |
-В каком случае при поразрядном умножении не происходило перехода через разряд: когда результат являлся однозначным числом или когда двузначным числом? (однозначным) -При решении примеров будем использовать алгоритм. 1) Записываю умножение в столбик. 2) Умножаю единицы. 3) Единицы ответа пишу под единицами, а десятки (если они есть) запоминаю. 4) Умножаю десятки. 5) К числу десятков прибавляю десятки из памяти. 6) 3аписываю десятки под десятками, сотни под сотнями и т.д. 7) Читаю ответ. |
Выдаю алгоритм.
Учебник №3, с.7
3 218 * 4 872 | Объяснение: Рассмотрим запись, которую выполнила Маша. Что означает надписанная сворку в разряде десятков цифра? Откуда она появилась и как она учитывается в результате? (При умножении единиц получилось двузначное число, которое состоит из десятков и единиц. |
4) Физкультминутка
Мы семь раз в ладоши хлопнем,
Восемь раз ногами топнем.
Прибавляем три к семи
Столько мы присесть должны.
5) Первичное закрепление. Учебник №4
-Выполните умножение с помощью алгоритма.
6) ТПО с.4 № 4
— Ребята, давайте определим условие и требование задачи. Подчеркните их согласно правилу (условие -красным карандашом, требование — синим карандашом).
— Обсудите в парах ход решения задачи.
Было | 9 н. по 12 ф. |
9н. | |
Всего наборов | ? |
Решение: 12*9=108 (ф.л) — в наборе по 12 штук. 28*9=252 (фл.)-в наборе по 28 штук. 108+252= 360 (фл.) Ответ: 360 фломастеров купили. | |
Попробуйте самостоятельно записать выражение этой же задачи с помощью выражения по схеме. (12+28)*9=40*9=360 Обменяйтесь тетрадями с соседом. | |
6) Итог урока:
-Достигли мы поставленной цели урока?
-Чему научились на уроке?
-Какие возникли затруднения и удалось ли их преодолеть?
7) Рефлексия.
Оцените свою работу на уроке.
С помощью смайликов покажите, как вы усвоили тему.
Все понял(а) | Не до конца разобрался (-лась) | Ничего не понял(а) |
Умножение на однозначное число столбиком
МБОУ «Могилевская СОШ им.Н.У.Азизова»
Конспект урока по математике «Умножение на однозначное число столбиком»
Класс: 4 УМК «Школа Росии»
Учитель начальных классов:Дадаева Марьям Касумовна.
Цели: выполнять умножение на однозначное число столбиком; совершенствовать вычислительные навыки; развивать логическое мышление, память и внимание.
Оборудование: карточки, таблица.
Ход урока
I. Организационный момент.
II. Устный счет.
Заполнить пропуски
Множитель | 20 | 50 | 12 | 14 | ||
Множитель | 70 | 15 | 40 | 16 | ||
Произведение | 240 | 840 | 720 | 960 |
2. Задача.
Мать старше дочери в три раза, а вместе им 48 лет. Сколько лет матери и дочери?
3. Рассмотрите чертеж.
– Какие геометрические фигуры здесь изображены?
– Сколько треугольников на чертеже?
4. Индивидуальная работа у доски
Вырази в указанных единицах измерения.
6см8мм= мм5км700м= м.
5м6см= мм 8км 8м= м.
6дм6см= мм 6дм3см= см.
5см2= мм2 90м2= см2
8дм2 5см2= см2 8км2= м2
5м2 6см2= см2 7дм2 5см2= см2
III. Сообщение темы урока.
Сообщение темы урока.
– Рассмотрите схемы на доске:
– Что обозначают данные схемы?
– Какие трудности у вас возникли?
– Сегодня на уроке будем учиться выполнять умножение на однозначное число столбиком.
IV. Работа по теме урока.
Задание 1.
– Проверьте, правильно ли выполнено умножение.
– Выпишите те случаи, в которых при поразрядном умножении не было перехода через разряд.
34 | 23 | 221 | 12 | 121 | 43 | 324 |
Х 2 | Х 3 | Х 4 | Х 3 | Х 4 | Х2 | Х 2 |
68 | 69 | 884 | 36 | 484 | 86 | 648 |
– Выпишите те случаи, в которых имел место переход через разряд.
Задание 2.
– Выполните умножение столбиком числа 273 на 3, отвечая на данные вопросы.
– Какое число получается при умножении в разряде единиц? (9.) Можно ли его сразу записать в разряд единиц результата? (Можно.)
– Какое число получается при умножении в разряде десятков? (21.) Сколько в 21 десятке содержится сотен и сколько еще десятков? (2 сотни 1 десяток.)
– Какую цифру мы записываем в разряд десятков результата? (2.) В какой разряд переходят 2 сотни? (В разряд сотен.)
– Какое число получается при умножении в разряде сотен? (6.) Сколько сотен перешло в этот разряд при выполнении умножения в предыдущем разряде? (2 сотни.)
– Сколько всего сотен получилось с учетом перехода? (8 сотен.) Какую цифру нужно записать в разряд сотен результата? (8.)
– В каком случае при поразрядном умножении не происходило перехода через разряд: когда результат являлся однозначным числом или двузначным? (Однозначным. )
)
Задание 3.
– Маша выполнила умножение числа 218 на число 4 столбиком.
– Что обозначает надписанная сверху в разряде десятков цифра 3? (Число десятков, которое запомнили.)
Задание 4.
– Выполните умножение числа 162 на число 4 столбиком.
– Объясните, как можно установить цифру каждого разряда результата. С какого разряда следует начинать вычисления? Почему? (Надо начинать умножение с разряда единиц.)
– К какому разряду следует переходить потом? (К разряду десятков.)
– Будет ли иметь место переход через разряд? (Да, запоминаем 2 сотни.)
Задание 5.
– Приведите примеры поразрядного умножения четырехзначного числа на однозначное, при выполнении которого дважды происходит переход через разряд: в разряде единиц и в разряде сотен.
1524 | 2514 | 1715 | 2415 |
Х 4 | Х 3 | Х 5 | Х3 |
6096 | 7542 | 8575 | 7245 |
Задание 6.
– Выпишите все трехзначные числа, при поразрядном умножении которых на число 5 не происходит перехода через разряд.
Задание 8.
– По данной схеме сформулируйте задачу, решить которую можно с помощью двух действий сложения или одного действия умножения.
– В одном ящике было 115 яблок, а в другом на 115 яблок больше. Сколько яблок всего? Для вычисления ответа задачи примените умножение столбиком.
Решение:
115 |
Х 3 |
345 |
Учащиеся выполняют умножение столбиком.
V. Итог урока.
– Как выполнить умножение многозначного числа на однозначное столбиком?
Домашнее задание. № 7.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/485423-umnozhenie-na-odnoznachnoe-chislo-stolbikom
Как умножать числа в одной или нескольких ячейках в Excel
Microsoft Excel — мощный инструмент; настолько мощный, что вы можете использовать его для выполнения основных математических уравнений. Например, если вы хотите умножать числа, вы можете сделать это в Excel относительно легко. Теперь вы можете умножать только в одной ячейке, более чем в одной ячейке и во всем столбце. В этом посте мы покажем вам, как умножать числа в одной ячейке и как умножать числа из нескольких ячеек в Microsoft Excel.
Например, если вы хотите умножать числа, вы можете сделать это в Excel относительно легко. Теперь вы можете умножать только в одной ячейке, более чем в одной ячейке и во всем столбце. В этом посте мы покажем вам, как умножать числа в одной ячейке и как умножать числа из нескольких ячеек в Microsoft Excel.
Знание того, как умножать в Microsoft Excel, очень важно для любого специалиста, студента и т. д. Начните с запуска Microsoft Excel на компьютере с Windows. Для этого найдите значок Excel на рабочем столе, панели задач или в меню «Пуск». Нажмите «Пустая книга», чтобы открыть новый лист Excel, или откройте лист, над которым вы уже работали ранее.
Как умножать числа в одной ячейке в Excel
Итак, после того как вы запустили Microsoft Excel и открыли рабочую книгу, пришло время выполнить умножение. Начнем с умножения чисел в одной ячейке.
Выберите ячейку, с которой вы хотите работать
Да, первое, что вы должны сделать здесь, это выбрать предпочтительную ячейку, щелкнув по ней. Видишь, как это было легко? Простой, но эффективный.
Видишь, как это было легко? Простой, но эффективный.
Введите правильную формулу
Следующим шагом будет ввод необходимой формулы для работы уравнения умножения. Формула, о которой идет речь, выглядит следующим образом:
=a*b
Убедитесь, что формула добавлена в область формул вверху, иначе вы, вероятно, столкнетесь с проблемами.
Умножение чисел в ячейке
После добавления формулы вернитесь в ячейку и замените a и b числами, которые вы хотите использовать. Например, если вы хотите умножить 27 на 15, введите в ячейку следующее:
= 27*15
Нажмите клавишу Enter, и теперь вы должны увидеть результаты.
Как умножить несколько чисел из нескольких ячеек в Excel
Может наступить момент, когда вы почувствуете необходимость перемножить числа, находящиеся в разных ячейках. Вопрос в том, как мы это делаем? Давайте поговорим об этом.
Добавьте числа в необходимые ячейки
Что вам нужно сделать прямо сейчас, так это добавить числа в соответствующие ячейки. Это числа, которые вы хотите рассчитать, поэтому убедитесь, что они верны.
Это числа, которые вы хотите рассчитать, поэтому убедитесь, что они верны.
Умножьте числа
Теперь, если числа находятся в A1 и A2, тогда формула должна выглядеть следующим образом:
=A1*A2
Имейте в виду, что вы захотите добавить формулу в другую ячейку. Например, вы можете добавить формулу в ячейку C1, чтобы там отображались правильные результаты.
Как умножить столбец чисел на постоянное число
Что касается умножения чисел в столбце, на это способен Excel. Как и следовало ожидать, задача очень похожа на умножение чисел в двух ячейках. Вам просто нужно внести изменения, основанные на здравом смысле. Однако с точки зрения умножения на постоянное число формула сильно отличается.
1Добавьте числа в столбец
Во-первых, вы должны добавить предпочтительный набор чисел в столбец. Вы можете решить, какой длины вы хотите, чтобы это было. Судя по изображению, наши номера варьируются от A1 до A8.
Выберите ячейку для постоянного числа
Теперь вам нужно выбрать ячейку для размещения постоянного числа. В этой демонстрации мы решили использовать C1, поэтому щелкните внутри и введите предпочитаемый постоянный номер
В этой демонстрации мы решили использовать C1, поэтому щелкните внутри и введите предпочитаемый постоянный номер
Выберите ячейку для результатов
Далее вы должны выбрать ячейку, в которой будут отображаться результаты. Мы решили работать с B1, так что вы тоже можете это сделать. Оттуда добавьте следующую формулу:
=A1*$C$1
Нажмите клавишу Enter на клавиатуре, и сразу же появятся результаты. Вы можете выполнить расчеты самостоятельно, чтобы убедиться, что Excel в порядке.
Чтение : Как создать калибровочную диаграмму в Excel.
Есть ли функция умножения в Microsoft Excel?
Да, в Microsoft Excel есть функция, поддерживающая умножение. Функция ПРОИЗВЕД умножает все числа, заданные в качестве аргументов, и возвращает произведение. Например, если ячейки A1 и A2 содержат числа, вы можете использовать формулу =ПРОИЗВЕД(A1, A2) , чтобы перемножить эти два числа. Вы также можете выполнить ту же операцию, используя математический оператор умножения (*); например, =А1 * А2 . Чтобы узнать больше об этом, вы можете посетить Microsoft.com. (Спасибо за это, Крис Такер – администратор)
Чтобы узнать больше об этом, вы можете посетить Microsoft.com. (Спасибо за это, Крис Такер – администратор)
Для чего используется Microsoft Excel?
Microsoft Excel — это программа для анализа и визуализации данных, более мощная, чем вы можете себе представить. Он использует электронные таблицы для организации, хранения и отслеживания наборов данных с помощью функций и формул. В профессиональной сфере Excel часто используется бухгалтерами, маркетологами, аналитиками данных и другими.
Умножение матриц
Изображение ARENA Creative на Shutterstock
Линейная алгебра может быть сложной для изучения. Однако очень важно, чтобы вы понимали это, а не просто запоминали, как выполняется каждая операция в линейной алгебре.
Понимание того, почему и как выполняются операции в линейной алгебре, требует логики и практики. Умножение матриц — это лишь одна из операций, охватываемых при изучении линейной алгебры в колледже, и для сдачи экзаменов требуется понимание того, как выполнять эту операцию вручную.
Давайте посмотрим, как выполнить матричное умножение между матрицей и скалярным числом, вектором или матрицей.
Что такое умножение матриц?
Линейная алгебра — относительно новая область изучения математики. В 1812 году французский математик Жак Филипп Мари Бине первым описал умножение матриц. Однако некоторые ученые ставят эту дату под сомнение, поскольку первая матрица не была полностью описана до 1857 года Артуром Кейли в Великобритании.
Чтобы понять, насколько «молодой» является линейная алгебра, приведем описание теоремы Пифагора в геометрии между 400 и 800 г. до н.э.
Матрица — это прямоугольный массив чисел или выражений. Он расположен в строках и столбцах. Количество строк представлено «m», а количество столбцов — «n».
Каждый элемент в матрице может быть представлен как «ai,j», где «j» увеличивается по отношению к столбцу, а «i» увеличивается по количеству строк, как вы можете видеть на рисунке ниже.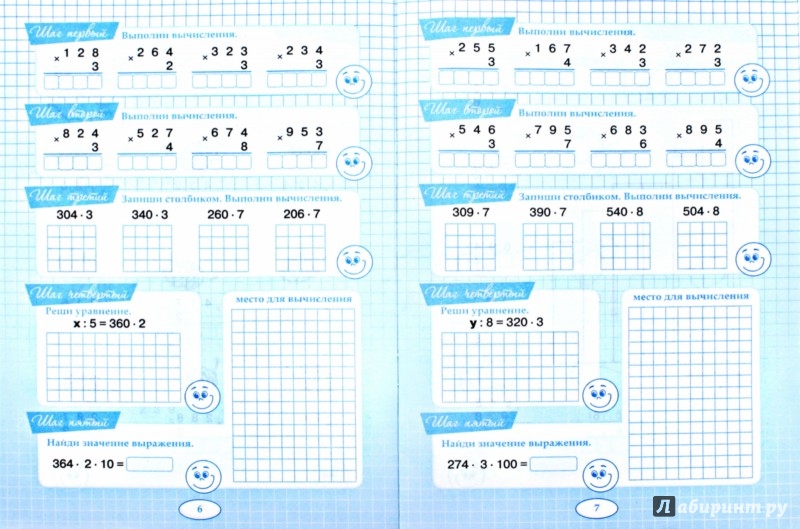
Фото Кредит
Как умножить матрицу на число
Умножить матрицу на число очень просто. Просто каждый элемент в матрице умножается на число. Стратегия не меняется в зависимости от количества строк и столбцов.
Когда число умножается на матрицу, это называется скалярным умножением. Скаляр — это величина, полностью описываемая одной величиной или числовым значением. В приведенном выше примере 3 является скаляром.
Как умножить матрицу на матрицу
Умножение между матрицами более сложное. Хотя вычисление результата умножения матриц вручную, вероятно, нецелесообразно в реальном мире, понимание процесса углубит ваше понимание линейной алгебры.
При умножении матрицы на матрицу количество столбцов в первой матрице должно равняться количеству строк во второй матрице, иначе операция не может быть определена.
Результатом будет матрица с m столбцами и p строками. Это представлено следующим уравнением:
Это представлено следующим уравнением:
[mn ][np] [mp]
Чтобы вычислить результат умножения матрицы на матрицу, вычислите «точечный продукт» каждой строки и столбца.
Скалярное произведение — это алгебраическая операция, при которой два списка чисел (векторов), равных по длине, возвращают одно число. Скалярный продукт также называется скалярным произведением, поскольку в результате вычисления получается одно число.
Матрицы разных размеров можно перемножать. Здесь у нас есть матрица A с «m» строками и «n» столбцами и матрица B с «n» строками и «p» столбцами.
Результатом матричного произведения является матрица C с «m» строк и «p» столбцов.
Для вычисления каждого элемента в матрице C используются приведенные ниже формулы.
Давайте рассмотрим пример. Здесь у нас есть матрица с 2 строками и 3 столбцами, умноженная на матрицу с 3 столбцами и 2 строками. В результате получится матрица с 2 строками и 2 столбцами.
В результате получится матрица с 2 строками и 2 столбцами.
Чтобы вычислить c1,1, мы должны определить скалярное произведение 1-й строки 1-й матрицы и 1-го столбца 2-й матрицы.
Формула выглядит следующим образом:
c1,1=2 (-1) +(-2) 3 +7 1 =-1
Аналогично вычисляется c1,2 путем определения скалярного произведения 1-го строку и 2-й столбец 2-й матрицы.
Формула выглядит следующим образом:
c1,2=2 5 +(-2)7 +7 9 =59
Для расчета c2,1 и c2,2 используются следующие уравнения:
c2,1=1 (-1) +8 3 +4 1 =27
c2,2=1 5 +8 7 +4 9 =97
Матрично-матричное произведение:
Как умножить матрицу на вектор
Вектор — это матрица только с одной строкой или только с одним столбцом. Умножение матрицы на вектор выполняется аналогично процедуре умножения матрицы на матрицу.
Здесь у нас есть вектор x=(4,-2,1), и мы умножаем его на матрицу A.
Вычислите c1,1, определив скалярное произведение 1-й строки, умноженной на вектор.
См. приведенное ниже уравнение для расчета c1,1.
c1,1=64 +2(-2) +41=24
Аналогично, вот уравнения для расчета c2,1 и c3,1.
c2,1 =-14 +4(-2) +31 =-9
c3,1 =-24 +9(-2) +31 =-23
Решение умножения матрицы на вектор имеет вид следующим образом:
В целом, умножение матрицы на вектор следует той же процедуре, что и умножение матрицы на матрицу. Тем не менее, важно соблюдать соглашения об именах.
Каков порядок действий?
В отличие от умножения действительных чисел, умножение матриц не является коммутативным. Например, результат не зависит от порядка элементов.
Например, в приведенном ниже расчете:
123=312=36
Обе части уравнения равны 36 независимо от порядка чисел. Это верно не для всех матриц. Коммутативные матрицы возникают, когда матрица умножается сама на себя или когда она умножается на единичную матрицу.
Это верно не для всех матриц. Коммутативные матрицы возникают, когда матрица умножается сама на себя или когда она умножается на единичную матрицу.
Например, у нас есть матрица A, умноженная на матрицу B, в результате получается матрица C.
Но если у нас есть матрица B, умноженная на матрицу A, конечным результатом будет другая матрица D.
Давайте сравним расчет для первого скалярного произведения, чтобы понять, почему существует разница.
При вычислении первого значения c1,1 используется формула:
c1,1=41 +3(-4) +14=-4
d1,1= 14 +2(-5) + 23 =0
Из того, как вычисляется скалярное произведение, ясно, что порядок имеет значение при умножении матриц. Обратите внимание, как подсвечиваются разные числа в матрицах при переключении порядка умножения матриц.
Как применять умножение матриц к реальным задачам
Умножение матриц имеет применение в реальном мире, даже если мы можем не думать об этих ситуациях как об умножении матриц.
Например, умножение матриц можно использовать для расчета прибыли магазина.
В таблице ниже указана стоимость каждого предмета, выставленного на продажу в магазине одежды.
В таблице ниже показано, сколько рубашек, свитеров и брюк было продано в понедельник, вторник и среду.
Прибыль в понедельник можно рассчитать по следующей формуле.
Прибыль за понедельник = Цена проданных рубашек + Цена проданных свитеров и свитеров
+ Цена проданных брюк Брюки
=122 + 304 + 604 =384
Знакомо? Мы только что рассчитали скалярный продукт для продаж в понедельник.
Представим эти данные в виде матрицы и вектора.
После умножения матриц мы можем рассчитать продажи в понедельник, вторник и среду ниже.
Приведенное ниже уравнение можно использовать для расчета прибыли во вторник.
Прибыль во вторник = c2,1=412 +1530 +1160 =1158
Аналогично, прибыль в среду можно рассчитать по приведенной ниже формуле.
Прибыль среды = c3,1= 412 + 230 + 160 = 168
Результирующая матрица 1 на 3 приведена ниже.
Матрицы и их операции также играют фундаментальную роль в понимании логики между массивами в программировании. Матрицы хранятся в виде массива массивов в программировании. Их также называют многомерными массивами.
Линейная алгебра лежит в основе многих передовых математических инструментов, таких как ряды Фурье и решение линейных уравнений. Он также играет ключевую роль в других областях, таких как статистика.
Краткий обзор специальных матриц
Некоторые матрицы неоднократно появляются в ходе исследования, и им присвоены определенные имена, чтобы их можно было легко идентифицировать.
Например, в нулевой матрице все значения просто равны 0.
Единичная матрица — это еще одна специальная матрица. Это квадратная матрица, в которой количество столбцов и строк равно. Диагональные значения, где «m» и «m» равны, равны 1.
Конкретные условия для единичной матрицы обозначаются:
Квадратная матрица, умноженная на единичную матрицу, не приведет к изменению квадратной матрицы. Например:
Для демонстрации расчета скалярного произведения первого значения используется следующая формула:
c1,1=91 + 40 + (-2)0 = 9
базовое упражнение по линейной алгебре и является обязательным курсом для большинства специальностей STEM. Освоение этой операции позволяет учащимся глубже понять линейную алгебру.
Убедитесь, что вы практикуете умножение матриц вручную. Легко пропустить число при вычислении скалярного произведения во время экзамена или теста.
 1 дec,)
1 дec,)
 Единицы записываем под единицами, десятки надписываем над десятками. 32=3 дес. 2 ед.)
Единицы записываем под единицами, десятки надписываем над десятками. 32=3 дес. 2 ед.)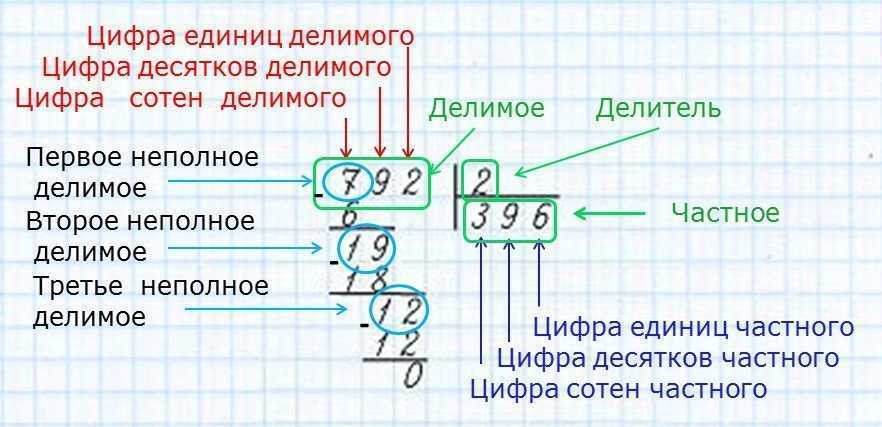 по 28 ф.
по 28 ф.