Карточки для тренировки по теме «Сложение и вычитание в столбик трехзначных чисел». — «Семья и Школа»
Содержание
Приёмы устного счета для быстрого вычисления в уме
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 — это дважды умножить на 2;
-
умножить на 6 — это значит умножить на 2, а потом на 3;
-
умножить на 8 — это трижды умножить на 2;
-
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 — это дважды разделить на 2;
-
разделить на 6 — это сначала разделить на 2, а потом на 3;
-
разделить на 8 — это трижды разделить на 2;
-
разделить на 9 — это дважды разделить на 3.

Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.

- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
УМНИКИ И УМНИЦЫ: ПРИМЕРЫ (ТРЕНАЖЕРЫ)
👌ГОТОВИМСЯ К ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЕ
Выполни по действиям:
602 630 – 297 480 : 37 · 69 + 8 653 =
424 410 : 47 – 261 + 608 · 34 =
3 807 · 98 + ( 550 701 – 82 989 ) : 64 =
2 603 · 58 + ( 100 000 – 19 975 ) : 75 =
170 604 : 36 + ( 60 700 – 358 · 47 ) =
( 258 270 + 8 090 · 67 – 366 860 ) : 48 =
Реши уравнения:
у — 584= 425 856- с = 412
х + 147 = 231 к — 4523 = 2354
4824 : у = 12 х : 220 = 700
15 х у = 255 а х 28 = 1680
Реши задачи:
😼Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
😼Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
😼С одного аэродрома одновременно в противоположных направлениях вылетели два самолёта. Один летел со скорость 420 км/ч, скорость другого на 80 км/ч меньше. Какое расстояние будет между ними через 3 часа?
😼Из гнезда одновременно в противоположных направлениях полетели две ласточки. Через 20 с расстояние между ними было 680 м. чему равна скорость одной из ласточек, если другая летела со скоростью
16 м/с?
😼Два мальчика одновременно вышли навстречу друг другу из своих домов. Один мальчик шёл со скоростью 50 м/мин, а другой со скоростью 65 м/мин. Через сколько минут они встретятся, если расстояние между домами 1035 м?
😼С двух льдин расстояние между которыми 1785 дм, одновременно навстречу друг другу поплыли два белых медведя .
😼Два автомобиля ехали с одинаковой скоростью. Один из них проехал 400 км, а другой — 480 км. Сколько часов был в пути каждый автомобиль, если первый был в пути на 2 часа меньше чем второй?
😼Два шофера возили зерно. Один из них сделал 3 рейса, другой — 5 рейсов за день. Второй шофер перевез на 30 т зерна больше, чем первый. Сколько зерна перевез каждый из шоферов по отдельности, если каждый рейс перевозилось одинаковое количество зерна?
😼Грузовики возили с базы муку в два разных магазина. В первый магазин отвезли 3 грузовика муки, а во второй 5. Сколько центнеров муки отправили в каждый магазин по отдельности, если в первый магазин отправили муки на 40 центнеров меньше, чем во второй?
👌ДЕЛЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО
| 6519 : 53 = | 1127 : 49 = | 4872 : 87 = | 288 : 24 = |
| 2805 : 33 = | 5037 : 73 = | 2812 : 76 = | 2870 : 35 = |
| 4268 : 44 = | 18228 : 28 = | 1450 : 25 = | 735 : 15 = |
243:14 3912:12 6405:15 10104:12
6372:12 10914:34 3945:15 7800:24
👌УМНОЖЕНИЕ НА ТРЕХЗНАЧНОЕ ЧИСЛО
👌УМНОЖЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО
👌ВЕЛИЧИНЫ
1. Вырази в миллиметрах.
Вырази в миллиметрах.
53 см =……..мм 6 м 46 см = ………мм
3 м 5 дм 8 мм = ……….мм 6 м 4 дм 8 мм = ……….мм
38 см =……..мм 7 м 26 см = ……мм
2. Переведи.
9000 м = ….. км 6040 м = ….. км ….. м 5001 м = ….. км …..м 730 см = ….. дм ….. см
306 мм = ….. см ….. мм 9005 мм = ….. м ….. мм
730 мм = ….. см
….. мм 39 см = ….. дм ….. см
527 см =
….. дм….. 39 мм =
….. см ….. мм
7030 мм =
….. м ….. мм 65200 м = …… км …… м
3. Напишите именованные числа в порядке
возрастания.
10 см, 20 мм, 9 дм, 11 км, 43 см, 8 мм, 5 м, 62 м, 7 дм.
1. Вырази в центнерах.
6 т 4 ц
5 т 200 кг 84000кг
2. Вырази
в тоннах.
2600 ц
57000 кг 69000ц
3.
Сравни.
329т… 331 ц
673ц… 375т
1000 кг… 1т
340 кг. .. 304 ц
.. 304 ц
901кг… 899 ц 871кг… 817 ц
4.
Переведи.
4000 г =… кг 26 т65 ц = … ц
62 т 5 ц = … ц 30 ц = … кг
УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
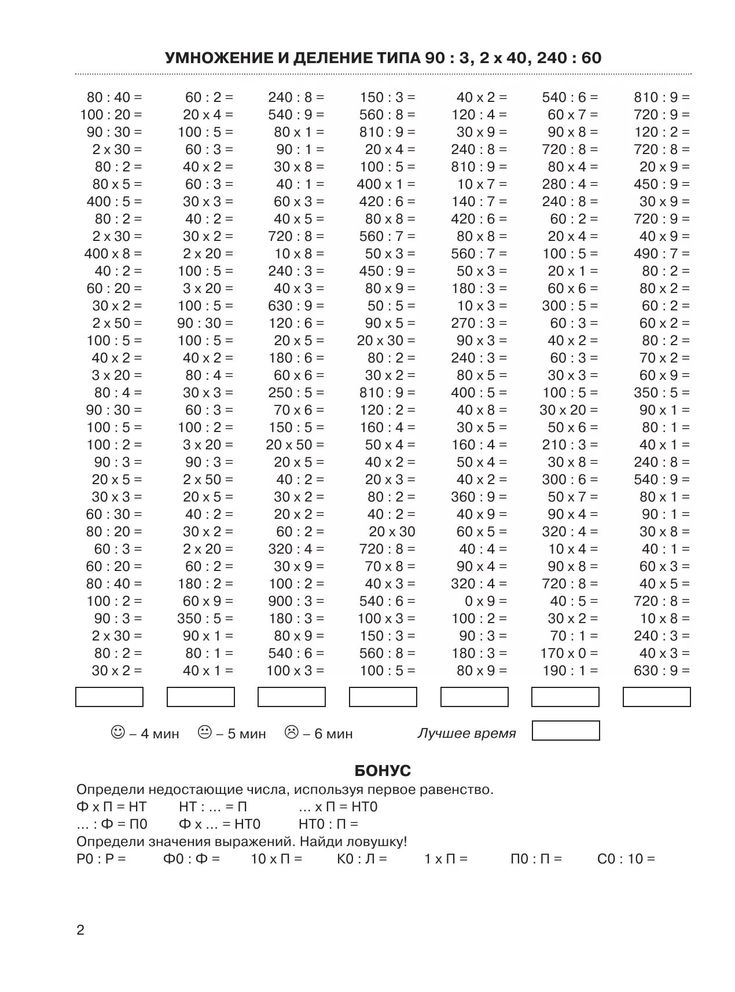
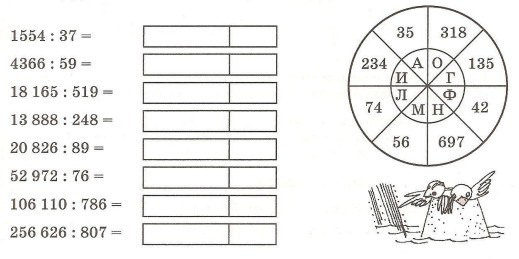
Раздели заданные многозначные числа на однозначное число.
| 1) | 37464 | 8 | 36830 | 5 | 39809 | 7 | 9314 | 1 | 16548 | 4 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | . .. | … | … | ||||||
| 2) | 7885 | 1 | 69616 | 8 | 12964 | 7 | 90369 | 9 | 6912 | 4 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 3) | 9396 | 9 | 10126 | 1 | 50301 | 9 | 18819 | 9 | 22536 | 3 | |||||
. .. .. | … | … | … | … | … | … | … | ||||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 4) | 5055 | 3 | 71010 | 9 | 75042 | 9 | 83862 | 9 | 13820 | 5 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | . .. | … | … | … | ||||||
| 5) | 52025 | 5 | 15230 | 2 | 14100 | 6 | 17346 | 7 | 2188 | 1 | |||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
| 6) | 25092 | 4 | 8126 | 2 | 16236 | 6 | 21352 | 2 | 23988 | 4 | |||||
. .. .. | … | … | … | … | … | … | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | ||||||
ЕДНИЦЫ ИЗМЕРЕНИЯ ПЛОЩАДИ
И ПЕРЕВОД ВЕЛИЧИН
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
УМНОЖЕНИЕ И ДЕЛЕНИЕ КРУГЛЫХ МНОГОЗНАЧНЫХ ЧИСЕЛ
РЕШИ
ДЕЛЕНИЕ ДВУЗНАЧНОГО НА ОДНОЗНАЧНОЕ
ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА
НА ДВУЗНАЧНОЕ
УМНОЖЕНИЕ И ДЕЛЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ
ПИСЬМЕННОЕ ДЕЛЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА
НА ОДНОЗНАЧНОЕ
нажми сюда
👇
Видео «Письменное деление»
Примеры для тренировки: 855 : 5 568 : 2 879 : 3
526 : 2 724 : 4 655 : 3
847 : 7 966 : 6 968 : 4
жми сюда и решай
👇
Письменное деление
Умножение: целые числа
Умножение можно рассматривать как многократное добавление. Итак, если вы умножаете число
а
по другому номеру
б
, это то же самое, что добавить число
а
снова и снова
б
раз. (Или добавление
б
снова и снова
а
раз). Например:
Итак, если вы умножаете число
а
по другому номеру
б
, это то же самое, что добавить число
а
снова и снова
б
раз. (Или добавление
б
снова и снова
а
раз). Например:
3 × 5 знак равно 5 + 5 + 5 знак равно 15 3 × 5 знак равно 3 + 3 + 3 + 3 + 3 знак равно 15
Другой способ думать об умножении целых чисел а × б состоит в том, чтобы визуализировать объекты, расположенные в виде прямоугольника, с а ряды и б столбцы.
3 × 5
Обратите внимание, что есть 15 точки на рисунке.
Стандартный алгоритм
Чтобы умножить многозначное число на однозначное с помощью стандартного алгоритма, напишите два числа друг над другом так, чтобы единицы были выровнены по вертикали, а многозначное число — сверху.
127 × 3 _
Умножьте цифру единиц верхнего числа на нижнее число. Запишите разряд единиц результата. Если результат больше 10 , несите цифру десятков, как при сложении.
Здесь, 7 × 3 знак равно 21 , так
1 2 2 7 × 3 _ 1
Теперь умножьте разряд десятков верхнего числа на нижнее число и прибавьте полученную цифру к результату.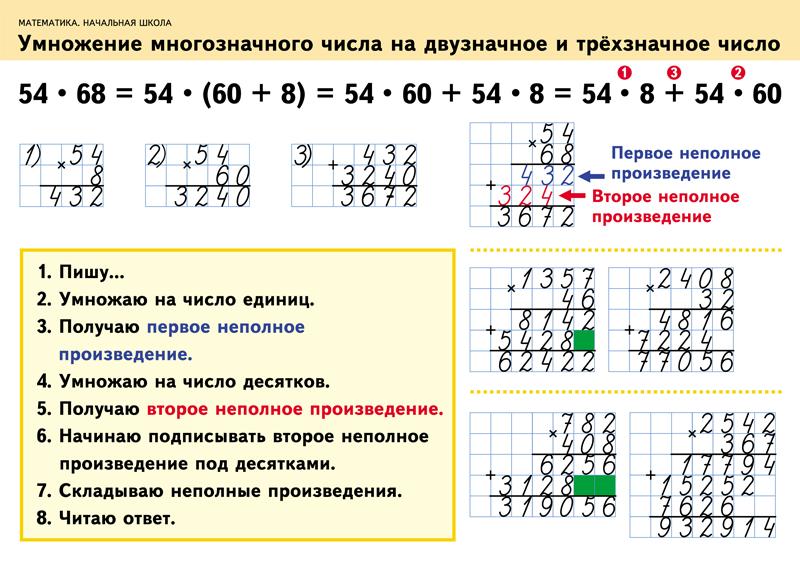 Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
1 2 2 7 × 3 _ 8 1
Наконец, умножьте разряд сотен верхнего числа на нижнее число. Здесь, 3 × 1 знак равно 3 .
1 2 2 7 × 3 _ 3 8 1
Так, 127 × 3 знак равно 381 .
Чтобы умножить два многозначных числа , напишите число с большим количеством цифр сверху. Например, чтобы умножить 29 по 543 , мы пишем
543 × 29 _
Сначала умножьте верхнее число на разряд единиц нижнего числа, как описано выше. 3 × 9 знак равно 27 , так что запишите 7 и нести 2 :
5 4 2 3 × 2 9_ 7
4 × 9 36, плюс 2 является 38 , поэтому запишите 8 и несите 3 :
5 3 4 2 3 × 2 9_ 8 7
5 × 9 является 45 , плюс 3 является 48 . Больше нет цифр для переноса, так что записывайте 48 .
5 2 4 2 3 × 2 9_ 4 8 8 7
Далее нам нужно умножить верхнее число на разряд десятков нижнего номера. Поскольку мы на самом деле умножаем на
20
, не по
2
, мы записываем
0
в качестве заполнителя.
5 4 3 × 29_ 4887 0
3 × 2 является 6 , поэтому запишите 6 .
5 4 3 × 2 9_ 4887 6 0
4 × 2 является 8 , поэтому запишите 8 .
5 4 3 × 2 9_ 4887 8 6 0
5 × 2 является 10 , и больше нет цифр для переноса, поэтому запишите 10 .
5 4 3 × 2 9_ 4887 10 860
Последним шагом является добавление двух результатов.
5 4 3 × 29_ 4887 + 10 860 _ 13947
Так, 543 × 29знак равно 13947 .
Как и сложение, умножение коммутативный для действительных чисел (т. а × б знак равно б × а ; порядок не имеет значения) и ассоциативный (то есть, ( а × б ) × с знак равно а × ( б × с ) ; группировка не имеет значения.) См. Свойства умножения для большего.
Шаблон плана урока Direct Instruction — Математика — Шаблон плана урока Direct Instruction
Шаблон плана урока Direct Instruction
Общая информация
Название урока: Умножение на многозначные числа Предмет(ы): математика Класс/Уровень/Настройка: 5-й Необходимые навыки/предварительные знания: Разрядное значение, факты умножения, умножение на однозначные числа
Стандарты и цели
Государственный/национальный академический стандарт(ы):
NBT. 5.A Умножение многозначных целых чисел Цели обучения: Учащиеся смогут решать задачи на умножение 4-значного числа на 2-значное, используя стандартный алгоритм с вероятностью 75%.
точность.
5.A Умножение многозначных целых чисел Цели обучения: Учащиеся смогут решать задачи на умножение 4-значного числа на 2-значное, используя стандартный алгоритм с вероятностью 75%.
точность.
Технология материалов
SmartBoard Диаграммная бумага Интерактивные тетради. Выходные билеты iPad
SAMR Уровень: Увеличение Использование активности SmartBoard, которую я также могу нажать в Google Classroom как физическое лицо или партнер деятельность позволяет практиковаться и получать немедленную обратную связь от меня.
Требования к языку
Особые способы использования учащимися академического языка (лексика, функции, дискурс, синтаксис) для участия
в учебных задачах посредством чтения, письма, прослушивания и/или разговора, чтобы продемонстрировать свое понимание. Языковые функции: Содержание и языковая направленность учебной задачи представлены активными глаголами в результатах обучения.
Словарь: Многозначное, разрядное значение, единицы, десятки, сотни, тысячи, множитель, произведение, умножение, перегруппировка, стандартный алгоритм, место держатель (или нулевой заполнитель), частичное произведение, множимое
Дискурс и/или синтаксис: Обсуждение: учащиеся будут участвовать в беседах о числах по поводу умножения, чтобы улучшить свои навыки устной речи. Синтаксис: учащиеся ведут интерактивные записные книжки с математическими таблицами и заметками.
Запланированная языковая поддержка: Студенты будут иметь очередь и время для разговора во время упреждающего набора, чтобы повторить то, что мы сделали вчера с умножением 4- цифра однозначными числами
Учебные стратегии и учебные задачи
Упреждающий набор: Описание занятия/Действия учителя и ученика Вопрос к учащимся: Что вы помните? со вчерашнего дня? (умножение 4-значного числа на 1-значное числа)
Обсуждение всей группой
Повернитесь и обсудите вопрос с партнером
Обсуждение всей группой
Поставьте цель обучения на день самостоятельно слова Процедуры представления новой информации и/или моделирования: Описание занятия/Действия учителя и ученика Лексика: повторение вчерашних слов (многозначное число, фактор, произведение, разрядное значение, единицы, десятки, сотни, тысячи, умножить, стандарт алгоритм, перегруппируйтесь) Познакомить с новыми словарными словами: место держатель (или нулевой заполнитель), частичный продукт, множимое Следующие определения будут поставлены на якорная диаграмма: Заполнитель: при умножении на число в разряде десятков (или сотен) необходимо добавить
Повернитесь и поговорите с напарником, чтобы просмотреть вчерашнее словарный запас
Скопируйте новые словарные слова в свои интерактивный блокнот
Скопируйте проблемы, которые я моделирую, в свои интерактивный блокнот
Что дальше? (7 х 4)
Что такое 7 х 4? (28) Я смоделирую как ты пишешь
вниз по 8 в столбце сотен и нести
2 Что будет дальше? (7 х 2)
Что такое 7 х 2? (14) смоделирую как вам нужно
добавить 2 к 14, чтобы получить 16, а 4 идет в
столбец тысяч и 1 идет в десятке
столбец тысяч Теперь, что мне нужно сделать? (поставить заглушку
нуль)
Что дальше? (9х 5)
Что такое 9 х 5? (45) Я смоделирую как ты пишешь
5 в столбце десятков и нести 4 Какой следующий шаг? (9 х 0)
Что такое 9 х 0? (0) смоделирую как вы добавите
4 вы перенесли на ноль и записали 4 в
столбец сотен Что будет дальше? (9 х 4)
Что такое 9 х 4? (36) Я смоделирую, как ты пишешь
6 в столбце тысяч и нести 3 Какой следующий шаг? (9 х 2)
Что такое 9 х 2? (18) смоделирую как вы добавите
от 3 до 18, чтобы получить 21 и написать 1 в десятке
столбец тысяч и 2 в сотне
тысяч столбец Что мы делаем, когда закончим
умножение? (добавьте 2 цифры) буду моделировать
добавление 2 чисел, показывающих, как это так
важно, чтобы у них все было в порядке
правильно Независимая студенческая практика:
Описание занятия/Действия учителя и ученика Я буду ходить и наблюдать за студентами, как
они работают над деятельностью Google Classroom. я
поможет, ответит на вопросы и прояснит
заблуждения по мере необходимости.
я
поможет, ответит на вопросы и прояснит
заблуждения по мере необходимости.
Учащиеся будут работать в Google Classroom на своих iPad для завершения самостоятельной работы. Они будут сможет продемонстрировать свой уровень понимание стандартного алгоритма и
На активности будут следующие проблемы: 5284 х 94 6301 х 32 2833 х 81 4025 х 40 3536 x 67
умножение многозначных чисел.
Кульминация или завершение процедуры/мероприятия: Описание занятия/Действия учителя и ученика Выходной билет Ученики продемонстрируют свои знания о стандартный алгоритм и умножение на 4 проблемы. 2039 х 23 4937 х 35 7251 х 44 1490 x 53
Учащиеся заполняют выходной билет показать свои знания об умножении и стандартный алгоритм.
Дифференцированное обучение
Подумайте, как приспособиться к потребностям каждого типа учащихся. Убедитесь, что вы предоставляете конкретное содержание
приспособления, которые помогают удовлетворить различные потребности в обучении.
Как научиться быстро считать в уме? — Meduza
1
Зачем в уме, когда можно на калькуляторе или в столбик?
Минимальные навыки счета, чувство числа — такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.
Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью — вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.
Подумайте и о том, что калькулятор и действия в столбик — это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «руками», ваше чувство контроля (и уверенности в себе) получает серьезный бонус.
И наконец, устный счет развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.
2
Но где брать задания для тренировки? Самому себе примеры придумывать?
Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.
При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решенных вами заданий.
Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.
3
А как именно нужно тренироваться?
Основных математических действий всего четыре — сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5−10 в день, и очень скоро вы почувствуете, что считаете лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.
4
И с чего же начать?
Начните с самого простого уровня — сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1−2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Допустим, вам нужно сложить 8 и 7.
1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).
2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).
3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек — получится 10 и 5, и это, конечно, 15.
5
Как складывать многозначные числа?
Здесь самый важный принцип — это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов — тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте все вместе.
Например, как сложить 456 и 789?
1) 456 состоит из трех разрядных частей — 400, 50 и 6.
789 тоже разбивается на три разрядные части — это 700, 80 и 9.
2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.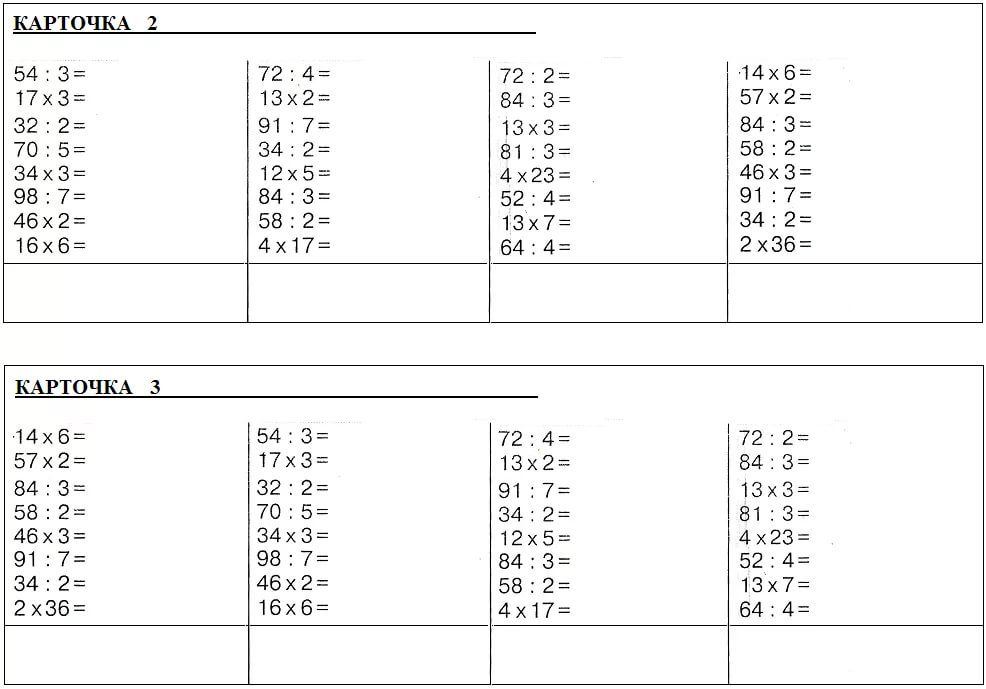
3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 — это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.
Поправка. При сложении разрядов мы перепутали единицы и к 6 прибавили 8 вместо 9. В итоге сумма тоже оказалась неправильной — 1244 вместо 1245. Приносим извинения за ошибку, и не повторяйте ее — внимательно следите за числами, особенно в устном счете!
6
Что насчет вычитания?
И здесь надо начинать с базового уровня — вычитания однозначного числа из чисел первого и второго десятка — и довести этот навык до совершенства. Как и в случае сложения, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».
Допустим, нам нужно из 12 вычесть 8.
1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).
2) Будем из 12 вычитать 8 по частям — сначала вычтем эту 2, а потом все остальное.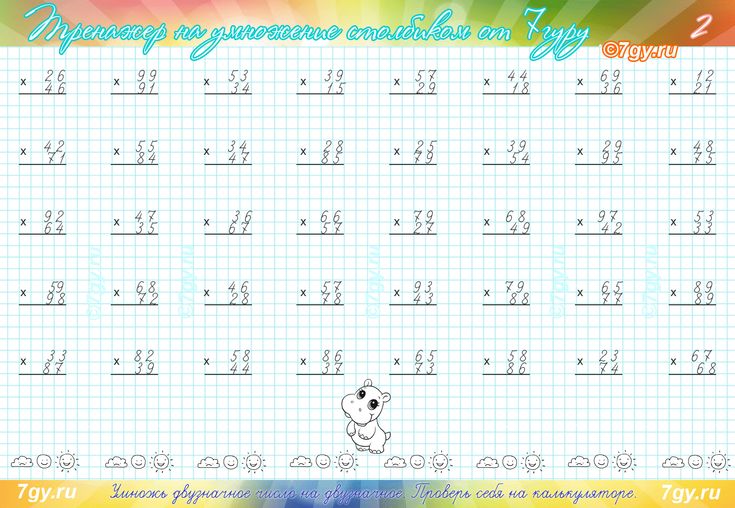 А остальное — это сколько? (это 6).
А остальное — это сколько? (это 6).
3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!
7
А что с многозначными числами? С ними все сложно?
Не особенно. Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Итак, допустим, нам нужно вычесть 512−259.
1) Число 259, которое мы вычитаем, состоит из трех разрядных частей — 200, 50 и 9. Их-то по очереди мы и вычтем.
2) 512−200 — вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой — 312.
3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.
Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем все остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.
4) Осталось вычесть единицы: 262−9.
Чистый переход через десяток — вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.
8
Как устроено умножение?
Начнем с умножения однозначных чисел. Для начала нужно вспомнить, что умножение — это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семерки. Пользуясь техникой сложения, мы можем легко посчитать — две семерки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвертую семерку, в результате получим 28.
Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семерок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семерку — получится 42.
Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
9
Как умножать многозначное число на однозначное?
Разберем на примере. Допустим, нам нужно умножить 468 на 6.
1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.
2) Идем от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).
Соответственно, 60∙6 = 360, а 8∙6 = 48.
3) А теперь, как при сложении, складываем все это вместе, группируя одинаковые разряды:
(2000+400)+(300+60)+(40+8) = [перегруппируем] =
= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =
= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =
= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.
10
Как перемножать двузначные числа?
Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счета. Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.
1) Эти 56 раз можно разбить на этапы — сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.
2) Число 78 сложить 50 раз несложно — это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.
3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.
4) Ну а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!
Поправка. На заключительном этапе при сложении 3900 и 468 мы неправильно разбили второе число на разряды — забыли про 60. В итоге в сумме получилось 4308. Приносим извинения за ошибку, и не повторяйте ее — нельзя терять в устном счете слагаемые.
11
Ничего себе, осталось последнее только действие, деление?
Да, мы на финишной прямой. И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
Итак, что же такое деление? По сути, это «обратная» операция к умножению.
Например, разделить 56 на 7 — значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число — это 8, 56:7 = 8.
И так всегда — вспоминайте, какое число при умножении дает нужный результат — это и есть то число, которое вам нужно.
12
Как делить многозначные числа на однозначное?
Давайте разделим 6144 на 8. Наш способ — «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.
1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 — это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
По ходу дела будем делить:
6144:8 = [выделяем максимальную удобную круглую часть] =
= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 700+544:8.
700 запомним как частичный результат, а сами займемся делением 544:8.
2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число — 56 — нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.
Продолжаем деление:
544:8 = [выделяем максимальную удобную круглую часть] =
= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 60+64:8.
60 добавим к 700, 700+60 = 760 — запомним это как вторую часть результата и перейдем к последнему делению, 64:8.
3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.
Соответственно, полный результат деления — это 760+8=768. Все!
Все!
13
Как делить на двузначное число?
Техника деления на двузначное число — самая разнообразная, непохожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.
1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки».
Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно.
В 4 раза больше, чем 20 — это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток.
Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.
2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.
Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так). Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).
3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78.
5148 явно ближе к 5280, поэтому сперва проверим 78.
78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура!
(Ну а если бы результат не сошелся, то мы бы проверили второе число, и оно бы уже точно подошло).
14
Какие рекомендации напоследок?
Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счета в пределах 10000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).
Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счета, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности — старайтесь заниматься на тренажере каждый день по 5−10 минут, больше не нужно, иначе велик риск «перегореть» и забросить.
В процессе занятия никуда не торопитесь — ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.
Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах — у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.
И не расстраивайтесь, если что-то не выходит — дорогу осилит идущий, и рано или поздно у вас точно все получится.
6 простых шагов по обучению умножению в игровой форме для учащихся
Переход от обучения вычитанию и сложению к обучению умножению является одной из самых сложных задач, с которыми учащиеся столкнутся в школе.
Проблемы с предметом возникают не только у студентов.
При обучении умножению преподаватели часто начинают с неправильных понятий или слишком быстро проводят уроки. Это может обескуражить и запугать учащихся, что в конечном итоге нанесет ущерб результатам обучения.
К счастью, существуют известные способы избежать этих препятствий.
Используйте приведенное ниже руководство, чтобы увидеть, как можно упростить преподавание и изучение умножения за шесть простых шагов, которые заинтересуют и найдут отклик у учащихся.
Раздел A: Руководство из шести шагов по обучению умножению 1. Свяжите умножение со сложениемНе начинайте с запоминания. Студенты обычно с трудом запоминают факты умножения с первой попытки, и это может привести к страху перед таблицей умножения.
Самый простой способ начать обучение умножению — это закрепить понятие с точки зрения его связи со сложением — операция, с которой ваши ученики уже должны быть знакомы.
Прежде чем двигаться дальше, убедитесь, что ваши ученики усвоили первый столп умножения: это просто повторяющееся сложение.
Используйте соответствующих примера , подобных приведенному выше, чтобы контекстуализировать этот факт.
Это поможет записать примеры, чтобы учащиеся могли визуализировать идею:
2 x 2 то же самое, что 2 + 2
или
3 x 4 то же самое, что 4 + 4 +
2. Начните с атлета и одного. Умножение на ноль: свойство нуля , любые 9Число 0070, умноженное на ноль, также равно нулю:n x 0 = 0
Предложите учащимся найти примеры нулевого свойства в комнате. Например, если в классе 25 стульев, на каждом из которых не сидит ни одной обезьяны, это означает, что в классе нет обезьян.
При желании один забавный пример забавного математического задания для развлечения ваших учеников включает в себя размышление о забавных примерах этого свойства, например 0 x один миллион = 0 . .. или … 0 x бутерброд с ветчиной = 0.
.. или … 0 x бутерброд с ветчиной = 0.
Источник изображения: Step Into 2nd Class
Умножение на единицу: свойство тождества само: n x 1 = n.Как и в случае с нулевым свойством, подчеркните в своем классе, что умножение числа на единицу приводит к тому же самому значению.
Чтобы обосновать свойство в контексте реальной жизни, предложите вашему классу подумать о экземплярах свойства идентичности в классе.
Например,
- Одна группа из восьми парт — это восемь парт
- Одна строка календаря, показывающая, что семь дней — это семь дней
Источник изображения: The Classy Teacher
3. Закройте таблицу умножения, начиная с «простыми» числамиДля повторения ваши ученики должны понять, что умножение можно рассматривать как многократное сложение.
Они также должны были потратить время на умножение чисел на ноль и единицу. Хотя им не нужно знать технические термины, понять, как работают нулевое свойство и свойство идентичности.
Хотя им не нужно знать технические термины, понять, как работают нулевое свойство и свойство идентичности.
Теперь пришло время сделать один из самых больших скачков: пройти таблицу умножения.
Один из эффективных подходов работает следующим образом:
- Показать таблицу или слайд таблицы умножения 12 x 12. Если хотите, дополните это студенческими копиями таблицы умножения. Если таблица 12 х 12 кажется слишком сложной, проделайте тот же процесс с таблицей умножения 10 х 10.
- Научите учащихся пользоваться диаграммой и находить продукты, следуя и сопоставляя положение чисел по вертикальной и горизонтальной осям.
- Теперь поговорим о некоторых паттернах, которые вы можете найти на графике. Предложите учащимся подсказки или подсказки. Например, обратите внимание, что каждое число, кратное десяти, заканчивается нулем, а каждое число, кратное пяти, заканчивается нулем или пятью.
- Спросите учащихся, какие факты даются легче всего.
 Например, единицы и десятки легко. Теперь, когда вы обсудили «простые» факты умножения и то, что делает их легкими, удалите их из таблицы.
Например, единицы и десятки легко. Теперь, когда вы обсудили «простые» факты умножения и то, что делает их легкими, удалите их из таблицы.
Студенты обычно соглашаются, что двойки, пятерки и одиннадцать тоже даются легко. Продолжайте вычеркивать «простые» числа, пока не дойдете до этапа, который выглядит примерно так:
- Посмотрите на оставшиеся числа вместе с классом. Используйте возможность вести динамичную дискуссию и перейти к следующему шагу.
Как и сложение, умножение коммутативно, означает, что порядок множителей не меняет произведение (ответ).
Другими словами, два числа можно умножать в любом порядке, и произведение будет одинаковым. Например, умножение 8 x 2 даст вам тот же ответ, что и умножение 2 x 8.
Когда вы эффективно донесете это, это поощрит ваших учеников.
Покажите своим ученикам, что каждый ответ повторяется, поэтому им нужно выучить только половину оставшихся таблиц. Например, объясните, что обучение 3 x 6 аналогично обучению 6 x 3!
Например, объясните, что обучение 3 x 6 аналогично обучению 6 x 3!
Если учащиеся уже усвоили факт семейства от 0 до 3, то они также знают четыре числа от 4 до 10.
Чтобы еще больше усилить свойство коммутативности, вы также можете использовать визуальную модель, подобную приведенной выше, и указать, как расположены желтые блоки.
Спросите своих учеников: «Разве эти две аранжировки не одинаковы, а просто разные версии друг друга? Если мы посчитаем общее количество единиц, они одинаковы?»
Помощь учащимся в понимании этого свойства является ключевой частью обучения умножению. Чтобы учащиеся делали это сами и учились на собственном опыте, пусть ваш класс создаст модели, иллюстрирующие эту идею, и докажет, что a x b приводит к тому же результату, что и b x a .
5. Разбейте заучивание на простые шаги Теперь ваши ученики готовы начать заучивание таблицы умножения . Вполне вероятно, что они уже начали это делать.
Вполне вероятно, что они уже начали это делать.
Имейте в виду, что учащимся не всегда очевидно, зачем им нужно заучивать факты умножения наизусть. Сообщите о важности понимания значения фактов умножения и о том, как их можно использовать в повседневных ситуациях.
Хотя существует множество подходов к запоминанию таблицы умножения, вспомните приведенные выше примеры — «простые» числа — в качестве хорошей отправной точки. Продолжая урок, соблюдайте следующие правила:
- Поощряйте учащихся и выделяйте время для устной или письменной практики.
- Вводите новые факты умножения один за другим , постепенно и поэтапно открывая концепцию более сложных шагов умножения на 2, 3, 4 и так далее.
- Дайте учащимся время потренироваться факты умножения. Найдите ритм, который хорошо работает в вашем классе. Если хотите, воспользуйтесь возможностью взаимного обучения для учащихся, испытывающих затруднения.

- Запомните факты в стратегическом порядке . Как только ваши ученики освоят 0–3 , переходите к 4–7 , а затем к 8–10 . В зависимости от ваших предпочтений, вы также можете охватить 11 и 12. Добавление более сложных задач в качестве бонуса поможет вам оценить успевающих учеников. Некоторые учителя будут включать несколько более сложных задач в качестве бонуса или для выявления отличников.
Чтобы облегчить запоминание, держите под рукой наглядные материалы в классе. Независимо от того, сколько раз вы повторяете умножение, всегда полезно иметь физическую копию таблицы в вашем классе.
Если у вас его нет, вы можете заказать его онлайн менее чем за 10 долларов. Быстрый поиск на Amazon показывает множество вариантов.
Если у вас уже есть плакат, рассмотрите возможность получения других материалов, которые помогут вам наглядно объяснить функцию умножения.
Например, этот документ является отличным вариантом для дисплеев: он содержит 20-страничный набор ответов (как тот, что показан ниже) на каждую из таблиц умножения от 1 до 10, окрашенных в соответствии с конкретной таблицей, которую они представляют.
Хотя эти понятия более сложные, важно, чтобы ваши учащиеся усвоили их. Вы обнаружите, что они могут творить чудеса, улучшая умственные способности ваших учеников.
Примечание: При вводе свойств, указанных ниже, действуйте по своему усмотрению. Они могут быть неприменимы к учащимся любого года младше 4-го класса.
Ассоциативное свойствоПравило 9Ассоциативное свойство 0003
утверждает, что независимо от того, как вы группируете факторы, продукт всегда будет одним и тем же.Например,
( A x B ) x C = A x ( B x C )
или 9005
(
). 3 = 1 x (2 x 3)
3 = 1 x (2 x 3) Ваши учащиеся могут понять эту концепцию, связав ее со сложением столбцов, посредством чего они группируют слагаемые, чтобы найти сумму.
Студенты также могут научиться группировать факторы любым удобным для них способом при поиске ответа. Вы можете объяснить это правило как расширение коммутативного свойства выше.
Свойство распределения Свойство распределения обозначается как a(b + c) = (ab) + (ac) 90 они уже используют это свойство сами по себе как математический трюк в уме для решения более сложных фактов умножения.
Проще говоря, свойство распространяется — или, как следует из его названия, распределяет — значение a поровну на b и c.
Например, для 6 x 8 они могут использовать распределительное свойство, чтобы думать: (6 x 5) + (6 x 3) или 30 +18
Чтобы объяснить это свойство визуальным или тактильных учащихся, позвольте детям исследовать распределительное свойство с помощью таких материалов, как чашки и бобы или сетчатая бумага.
Математические игры в классе могут избавить от страха перед умножением. Рассмотрим эти два примера, посвященные умножению:
Константы калькулятора
Если калькуляторы в вашем классе имеют функцию констант, предложите учащимся использовать их для определения кратности любого числа, чтобы найти связь между умножением и сложением.
Как это работает:
- Выберите коэффициент, например семь, и введите его.
- Нажмите кнопку +, затем нажмите кнопку =. Калькулятор должен снова показать семь.
- Далее продолжайте нажимать кнопку =. Константная функция будет постоянно добавлять семь, показывая возрастающие множители числа (7, 14, 21, 28 и т. д.)
- При желании учащиеся могут записать список найденных кратных чисел и предложить им искать закономерности в списке. они придумали
Times Table Buzz
Это веселое математическое задание, которое мотивирует ваших учеников и закрепляет их знания о таблице умножения.
Шаг а) Выберите конкретную таблицу умножения для использования в упражнении (например, число, кратное пяти)
Шаг б) Попросите учащихся встать и расположить их в определенном порядке, чтобы каждый учащийся знал когда подходит их очередь
Шаг c) Выберите одного ученика, чтобы считать «один». Затем ребенок слева от него считает «два». Следующий ребенок считает «три» и так далее. Когда последовательность достигает числа, кратного пяти, учащийся выкрикивает «жужжание!»
Следовательно, последовательность будет следующей: раз, два, три, четыре, « жужжание !», шесть, семь…
Шаг d) Если учащийся забывает сказать «жужжание» или произносит его в неподходящее время они выходят и садятся. Последовательность подсчета будет продолжаться до тех пор, пока учащиеся не наберут десять раз по пять (или по усмотрению учителя), а затем начнется снова.
Окончательными победителями становятся трое последних выживших детей. Рассмотрите возможность награждения победителей как часть вашей стратегии управления классом.
Рассмотрите возможность награждения победителей как часть вашей стратегии управления классом.
Чтобы получить больше вдохновения, просмотрите наш полный список из 20 увлекательных математических игр для развития навыков.
Для активного подхода к обучению математике ознакомьтесь с нашими 20 веселыми и творческими математическими заданиями — подходами и упражнениями с компьютерами и без них, которые заставят учащихся с нетерпением ждать ваших уроков математики.
Используйте забавные учебники по математике в классеВ нашем обзоре учебников по математике для учащихся мы нашли список исключительных ресурсов для учителей.
Просмотрите номера три, пять и шесть, чтобы найти примеры публикаций, в которых используется умножение и которые помогают поддерживать хорошо структурированную учебную программу по математике.
Поддержка обучения с помощью веб-сайтов по математике Интернет является домом для огромного количества мощных и полезных образовательных математических веб-сайтов для учителей и учащихся.
См. наш список полезных математических веб-сайтов для учителей, пятью из которых вы можете поделиться со студентами. Одним из ресурсов является Prodigy Math Game, математическая игра, ориентированная на учебную программу, которую используют более 800 000 учителей и 30 миллионов учащихся по всему миру.
Prodigy предлагает контент по всем основным темам математики, включая умножение, и предназначен для учащихся с 1-го по 8-й класс.
Вы можете превратить изучение умножения в фантастическое путешествие, в котором успех учащихся зависит от оттачивания математических навыков, соответствующих учебной программе!
Зарегистрируйтесь сейчас Как преподавать умножение: Заключительные мыслиЕсли умножение — это наука, то помощь ученикам в понимании операции — это искусство.
Имея в виду эти стратегии и инструменты, вы можете понять, что умножение не обязательно должно быть пугающим или обескураживающим предметом — для вас или ваших учеников.
При разбивке на удобоваримые составляющие вы избежите разочарований, которые часто сопровождают практику обучения умножению.
Используйте эти идеи, чтобы усилить хорошо структурированную учебную программу по математике, и наблюдайте, как улучшаются результаты обучения ваших учеников.
МУЛЬТИ в Excel | Примеры выполнения умножения матриц в Excel
Excel МУМНОЖ ( Содержание)
- Что такое функция МУМНОЖ в Excel?
- Примеры MMULT в Excel
С математической точки зрения явление умножения двух матриц друг на друга называется умножением матриц. Однако умножение двух матриц имеет определенные правила. Поскольку произведение матриц дается путем умножения элементов каждой строки первой матрицы на элементы каждого столбца второй матрицы, становится обязательным, чтобы количество столбцов первой матрицы было равно количеству строк второй. матрица.
Что такое функция МУМНОЖ в Excel?
В Excel у нас есть функция под названием «MMUL», функция массива, которая является частью множества формул в функции «Математика и тригонометрия», которую можно найти в разделе «Формулы». MMULT можно использовать для получения произведения двух массивов матриц в Excel, в котором количество строк из первой матрицы равно количеству столбцов из второй матрицы.
MMULT можно использовать для получения произведения двух массивов матриц в Excel, в котором количество строк из первой матрицы равно количеству столбцов из второй матрицы.
Синтаксис:
Ниже приведен синтаксис функции МУМНОЖ в Excel.
Аргументы:
- array1 — Обязательный аргумент для функции, указывающей первый массив матриц, который вы хотите умножить.
- array2 — Обязательный аргумент для функции, указывающей второй массив матриц, который вы хотите умножить.
Запятая разделяет оба этих аргумента в функции МУМНОЖ. Это означает, что после того, как вы ввели первый массив в формулу, вы должны упомянуть запятую («,»), прежде чем добавлять второй аргумент массива.
Как уже упоминалось в начале, МУМУЛЬТИМЕТР является функцией массива. Таким образом, при его выполнении вам нужно одновременно нажать кнопку Ctrl + Shift + Enter вместо прямого нажатия клавиши Enter на клавиатуре.
Примеры MMULT в Excel
Давайте рассмотрим несколько примеров на практике.
Вы можете скачать этот шаблон MMULT Excel здесь — Шаблон MMULT Excel
Пример 1. Использование MMULT для умножения двух матриц
Предположим, у нас есть две матрицы с двумя строками, тремя столбцами и тремя строками и двумя столбцами соответственно, как показано ниже.
После того, как мы перейдем к произведению этих двух матриц, они в лучшем случае могут дать две строки и два столбца (это потому, что у нас есть две строки в первой матрице и два столбца во второй матрице). Следовательно, наша результирующая матрица будет матрицей 2X2. Мы будем хранить то же самое в ячейках, варьирующихся от A6: B8, как показано ниже:
Шаг 1: Выберите все ячейки (A7:B8) из результирующей матрицы, чтобы сразу применить формулу.
Шаг 2: Внутри активной ячейки (ячейка A7) начните ввод формулы для умножения матриц. Используйте =МУМНОЖ( в ячейке, чтобы инициировать формулу.
Используйте =МУМНОЖ( в ячейке, чтобы инициировать формулу.
Шаг 3: Используйте ячейки первой матрицы, т. е. от A2 до C3, в качестве первого аргумента массива в формуле для умножения матриц. Поставьте запятую (» ,») после установки первого массива в формуле.
Шаг 4: Используйте ячейки второй матрицы, т. е. от E2 до F4, в качестве аргумента второго массива по формуле для умножения матриц. Закройте скобки, чтобы завершить эту формулу.
Шаг 5: Теперь формула готова. Но не нажимайте кнопку Enter напрямую. Помните, что функция МУМНОЖ является функцией массива. Вместо нажатия Enter используйте Ctrl + Shift + Enter , чтобы получить вывод этой формулы.
Вы получите результат умножения/произведения двух матриц в ячейках A7:B8, как показано ниже:
Обратите внимание на фигурные открывающие и закрывающие скобки, в которые заключена формула для MMULT. Эти фигурные скобки указывают на то, что введенная нами формула является формулой массива или применяется к массивам.
Эти фигурные скобки указывают на то, что введенная нами формула является формулой массива или применяется к массивам.
Как работает формула? Давайте посмотрим ниже:
Умножение матриц похоже на то, что каждый элемент каждой строки из первой матрицы умножается на каждый элемент каждого столбца из другой матрицы. Затем мы суммируем все значения по элементам, чтобы получить одно значение. Первая строка для первой матрицы — это 2, 6, 3, а первый столбец второй матрицы имеет значения 2, 7, 4. Продолжая поэлементное умножение, мы получим —
(2*2) = 4, (6*7) = 42 и (3*4) = 12 в результате умножения. Теперь мы сложим эти три значения вместе, чтобы получить первый элемент результирующей матрицы.
4 + 42 + 12 = 58.
Таким образом, первым элементом результирующей матрицы будет 58.
Пример 2. Использование MMULT для умножения двух матриц
Предположим, у нас есть две матрицы с тремя строками, как показано ниже. и три столбца:
Мы будем использовать MMULT, чтобы получить произведение этих двух матриц и получить из него новую матрицу, называемую результирующей матрицей, которую можно сохранить в A7: C9. .
.
Поскольку у нас есть три строки в первом столбце и такое же количество столбцов во второй матрице, результирующая матрица будет матрицей с тремя строками и тремя столбцами.
Шаг 1: Выберите все ячейки в A7:C9 в Resultant Matrix и введите формулу для МУМНОЖ в ячейке A7.
Шаг 2: Используйте первую матрицу в качестве первого аргумента функции МУМНОЖ, которая распределена по ячейкам A2:C4. Используйте запятую, чтобы отделить первый аргумент от второго.
Шаг 3: Используйте вторую матрицу в качестве аргумента второго массива в функции МУМНОЖ, которая распределена по E2:G4. Завершите формулу, добавив закрывающую скобку.
Шаг 4: Теперь нажмите Ctrl + Shift + Enter , чтобы получить вывод этой формулы массива вместо нажатия клавиши Enter. Вы получите вывод, как показано ниже:
Вот как мы можем использовать функцию МУМНОЖ, чтобы получить умножение матриц для двух массивов матриц.


