Математика 6 класс. Все тесты и тренажеры
Выберите необходимый Вам учебно-методический комплекс для прохождения онлайн-тестирования по предмету «Математика 6 класс»:
Тесты для УМК Виленкин (21 тест)
Тесты для УМК Мерзляк (7 тестов)
Тесты для УМК Никольский (48 тестов)
Тесты для УМК Зубарева (25 тестов)
Тесты для УМК Дорофеев (14 тестов)
По окончании выполнения теста ученик может направить результаты тестирования на свой адрес электронной почты, а затем на адрес эл.почты своего учителя, либо сразу (напрямую) отправить результаты тестирования своему учителю.
Контрольные работы с ответами. 6 класс
УМК МЕРЗЛЯК: Дидактические материалы: Контрольные работы (12 КР)
УМК МЕРЗЛЯК: Дидактические материалы: Самостоятельные работы (37 СР)
УМК ВИЛЕНКИН: Попов.
Дидактические материалы по математике (10 КР)
УМК ВИЛЕНКИН: Жохов. Контрольные работы по математике (15 КР)
УМК ВИЛЕНКИН: Попова. Контрольно измерительные материалы (15 КР)
УМК ВИЛЕНКИН: Ершова и др. Контрольные и самостоятельные работы (итоговая КР)
УМК НИКОЛЬСКИЙ: Потапов. Дидактические материалы; контрольные работы (9 КР)
УМК ДОРОФЕЕВ: Кузнецова, Минаева и др. Контрольные работы (8 КР)
УМК ДОРОФЕЕВ: Смирнова. СиКР: Контрольные работы в 6 кл.
УМК КОЗЛОВА, РУБИН: Контрольные работы по математике в 6 классе
УМК ЗУБАРЕВА: Рудницкая. Дидактические материалы: Контрольные (11 КР)
К любому УМК — Дудницын и др. Контрольные работы по математике 6 кл (итоговая КР)
Регулярное выполнение работ с тестами и контрольных работ поможет учителям и учащимся своевременно получать информацию о полноте усвоения учебного материала.
Тематические тесты могут быть включены в урок на любом этапе: актуализации знаний, закрепления изученного, повторения. Онлайн форма тестирования внесет разнообразие в контроль и коррекцию знаний, умений и навыков, не отнимут много времени у учителя. В то же время анализ выполнения тестов поможет выделить повторяющиеся ошибки как индивидуально у каждого ученика, так и в целом по классу.
ВПР-2020 по математике 6 класс. Тренировочный тест !
Опорные конспекты по математике 6 класс.
Конспекты по математике 5-6 классы.
Онлайн-учебник: Математика 6 кл. / Мерзляк, Полонский, Якир.
Рекомендуемые материалы для очного контроля знаний
по предмету «Математика 6 класс»:
Дидактические материалы по математике. 6 класс. К учебнику Виленкина Н.Я. и др. — Попов М.А. (2017 -128с.)
Контрольные и самостоятельные работы по математике. 6 класс. К учебнику Виленкина Н.
Я. и др. Попов М.А. (2016, 96с.)
Математика 6 класс. Задания для обучения и развития учащихся. Беленкова Е.Ю., Лебединцева Е.А. (2013; 336с.)
Математика 6 класс. Контрольные измерительные материалы. Глазков Ю.А., Ахременкова В.И., Гаиашвили М.Я. (2014, 96с.)
Математика 6 класс. Контрольные работы. Жохов В.И., Крайнева Л.Б. (2011, 63с.)
Математика 6 класс. Практикум. Готовимся к ГИА. Шестакова И.В. (2014, 128с.)
Математика 6 класс. Тестовые материалы для оценки качества обучения. Гусева И.Л. и др. (2012, 96с.)
Самостоятельные и контрольные работы по математике для 6 класса. Ершова А.П., Голобородько В.В. (2013, 192с.)
Тесты по математике. 6 класс. Журавлев С.Г., Ермаков В.В. и др. (2015, 128с.)
Тесты по математике. 6 класс. К учебнику Виленкина Н.Я. и др. — Рудницкая В.Н. (2013, 144с.)
Сборник практических задач по математике. 6 класс. Выговская В.В. (2012, 64с.)
Математика. Дидактические материалы. 6 класс. Брагин В.Г., Уединов А.Б., Чулков П.В. (2005, 160с.
)
Математический тренажер. 6 класс. Жохов В.И. (2013, 95с.)
Математика. 5-6 классы. Тесты. Тульчинская Е.Е. (2014, 96с.)
Сборник задач и упражнений по математике. 6 класс. Гамбарин В.Г., Зубарева И.И. (2011, 95с.)
Дидактические материалы по математике. 6 класс. К уч. Зубаревой И.И., Мордковича А.Г. — Рудницкая В.Н. (2014, 128с.)
Тесты по математике. 6 класс. К учебнику Зубаревой И.И., Мордковича А.Г. — Рудницкая В.Н. (2013, 112с.)
Математика. 6 класс. Тематические тесты (к учебнику Никольского). Чулков П.В., Шершнев Е.Ф., Зарапина О.Ф. (2014, 128с.)
Математика. 6 класс. Дидактические материалы. Потапов М.К., Шевкин А.В. (2017, 128с.)
Контрольные и самостоятельные работы по математике. 6 класс. Журавлев С.Г., Изотова С.А., Киреева С.В. (2015, 224с.)
Контрольные работы по математике. 6 класс. Дудницын Ю.П., Кронгауз В.Л. (2013, 96с.)
Математика. 6 класс. 176 диагностических вариантов. Астанина Е.В., Радаева Е.А. (2013, 192с.)
Математика. 6 класс.
Итоговая аттестация. Типовые тестовые задания. Гаиашвили М.Я., Ахременкова В.И. (2015, 48с.)
Математика. 6 класс. Тематические тестовые задания для подготовки к ГИА. Донец Л.П. (2012, 128с.)
Математика. 6 класс. Тематические тесты. Промежуточная аттестация. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. (2012, 160с.)
Математика. 6 класс. Тематические тесты. Тренажер. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. (2014, 128с.)
Математика. 6 класс. Тестовые задания. В 2 ч. Истомина Н.Б., Горина О.П. (2014; 104с., 156с.)
Проверь себя. Тесты по математике. 6 класс. Минаева С.С. (2016, 112с.)
Вернуться
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
баллы | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 3 | 3 | 3 | Оценка |
1-5 | «2» | ||||||||||||||
6-9 | «3» | ||||||||||||||
10-15 | «4» | ||||||||||||||
16 | «5» | А. 75% | |||||||||||||
2. | Б. 100% | ||||||||||||||
3. | В. 10% | ||||||||||||||
4. | Г. 50% | ||||||||||||||
5. 1 | Д. 25% | А. 52,6 | |||||||||||||
2. | Б. 1,37 | ||||||||||||||
3. 52 | В. 52, 06 | ||||||||||||||
4. 52 | Г. 1,037 | А) 25% | |||||||||||||
2. | Б) 75% | ||||||||||||||
3. | В) 50% | ||||||||||||||
4. | Г) 10% | А) 61,6 | |||||||||||||
2. 2 | Б) 2,31 | ||||||||||||||
3. 61 | В) 2,031 | ||||||||||||||
4. 61 | Г) 61,06 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
ОТВ |
|
|
|
|
| 1,2139 |
|
|
| 1Г | 1Г | В |
|
|
|
Б | В | Б | А | В | 17450 | 0,18 | 3 | 3780 | 2Д | 2Б | 49,32м | 64,3га | 40 | ||
|
|
|
|
| 31451,2 |
|
| кг | 3А | 3D |
| 92,5га | 80 | ||
|
|
|
|
| 0,027 |
|
|
| 4В | 4А | 4Г |
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
ОТВ |
|
|
|
|
| 8,754 |
|
|
| 1В | 1В | Г |
| 23,5га |
|
Г | Б | Б | В | В | 87540 | 7,3 | 4 | 102 | 2А | 2Б | 80,3 | 56,4га | 52 | ||
|
|
|
|
| 0,00384 |
|
| уч | 3Б | 3Г | км |
|
| ||
|
|
|
|
| 4,7 |
|
|
| 4Г | 4А |
|
|
| Уч-ся по списку | Выполняли контрольную работу | Получили оценки | Качество знаний(%) | Обучен ность (%) | Учитель: |
5 | 4 | 3 | 2 | ||||||||||||
6 | 12 | 11 | 4 | 2 | 5 | — | 55 | 100 | Березовская ДИ. | ||||||
05.1998 №1276).
Каждому элементу левого столбца соответствует только один элемент правого.
Если при верном ходе решения задачи допущена ошибка, не носящая принципиального характера, и не влияющая на общую правильность хода решения, то в этом случае учащемуся засчитывается балл, который на один балл меньше указанного.
В яблоневом саду собрали 8400 кг яблок. На долю антоновских яблок приходится 45% всего урожая. Сколько килограммов антоновских яблок собрали в саду?
Расположите в порядке убывания числа: 1,583; 1,045; 1,451; 0,407; 1,513.
Из них 85% работали летом на ферме. Сколько учащихся старших классов работали летом на ферме?
В понедельник туристы прошли на лыжах 27,5 км, во вторник они прошли на 1,3 км больше, чем в понедельник. В среду туристы прошли в 1,2 раза меньше, чем во вторник. Сколько всего километров прошли туристы за эти три дня?
Математика: Тесты: Рабочая тетрадь. 6 класс.- М.: Рольф: Айрис –пресс,1999.
30 вопросов, которые нужно ответить на высший балл Математика 6-го класса — Best Life
Если ваша карьера не привела вас к математике или инженерному делу, скорее всего, вы не занимаетесь вычислением тригонометрических функций или сложными вычислениями на регулярной основе.
Но вы, вероятно, используете основные математические понятия, которые вам приходилось осваивать в начальной школе, почти каждый день, выясняя, как расставить мебель в гостиной или как сократить время на дорогу до работы.
Тем не менее, несмотря на то, что вы используете множество концепций из шестого класса, вы, вероятно, уже давно не повторяли то, что знаете на самом деле, и вас могут удивить ваши математические пробелы. Чтобы проверить, что вы знаете — и, что более важно, чего не знаете — вот 30 вопросов, с которыми справится любой отличник-шестиклассник. (Примечание: уровень сложности увеличивается!) И чтобы узнать больше о тестах, которые вы можете или не можете пройти, посмотрите, как наш репортер прошел президентский когнитивный тест (и вот они набрали баллы).
«-» здесь показывает, что это отрицательные числа, что означает, что они меньше нуля.
Минус 2 больше минус пять. Чтобы помочь вам думать об отрицательных числах, подумайте о настольной игре, где «больше» означает «ближе к финишу».
Представьте, что красная и синяя фигуры начинаются с одной и той же точки (нуля). Красная фигура должна вернуться на 2 клетки (-2). Синяя фигура должна вернуться на 5 делений (-5). Кто из них ближе всего к финишу? Красный!
Бьюсь об заклад, вы не знали, что вам придется учить новые слова на уроке математики! И чтобы отполировать свой нематематический словарный запас, начните с заучивания этих 47 крутых иностранных слов, которые заставят вас звучать безумно изощренно.
Дроби — это числа, разделенные по вертикали символами «-» или «/». В десятичных числах есть точка, которая в математике называется десятичной точкой. Целые числа — это числа без дробей и десятичных точек, даже если они отрицательные числа. А чтобы узнать больше о способах обострить свой ум, попробуйте эти головоломки, чтобы узнать, умнее ли вы астронавта.
Подсказка: если вы не помните, как переводить проценты в десятичные дроби, просто удалите знак процента и сдвиньте запятую на два знака влево.
0,85 x 21 = 17,85 Или, выражаясь в предложении, 85% от (x) 21 равно (равно) 17,85.
Освойтесь с десятичными дробями — вам нужно знать, как складывать, вычитать, умножать и делить их.
Складывать и вычитать десятичные числа не так сложно, как кажется. Просто не забудьте выровнять десятичные точки и поставить нули во всех правых столбцах, в которых нет чисел, если это необходимо (например: 8,563 0 + 4,8292). И еще несколько головоломок: посмотрите, как наш корреспондент сдал когнитивный экзамен НФЛ и вот что они узнали.
Это простое алгебраическое выражение. Алгебра — это просто использование символов в математике.
Любая буква может использоваться как переменная (или неизвестное число). В данном случае это строчная буква «u». Так что просто подставьте число в переменную, и вы получите 47 — 23 = 24. Далее Улучшите свой мозг с помощью этого научно доказанного трюка!
Это называется алгебраическим уравнением , потому что число по обе стороны от знака равенства должно быть одинаковым.
Поскольку мы знаем, что w означает неизвестное число, а числа по обе стороны от знака равенства должны совпадать, мы спрашиваем: «Какое число можно вычесть из 9, чтобы получить 8?»
Эти математические утверждения называются неравенствами. В отличие от уравнений, числа по обе стороны от < или > не обязательно должны быть равны.
Если вы прочтете это вслух, вы скажете: «6 меньше 7», поэтому < — это символ «меньше». Если вы перевернете его и напишете «7 > 6», получится «7 больше 6». Итак, > — это символ «больше чем».
Независимые и зависимые переменные также используются в научных экспериментах.
Независимая переменная — это то, что вы можете контролировать — в этом случае вы можете решить, сколько работы по дому выполнять. Зависимая переменная — это то, что зависит от независимой переменной — в этом случае, сколько денег вы зарабатываете, зависит от того, сколько работы вы выполняете. Это число будет меняться по мере изменения независимой переменной.
А чтобы узнать больше о способах повышения квалификации, начните с передовых видеоигр, которые сделают вас умнее.
ae0fcc31ae342fd3a1346ebb1f342fcb
Изучение треугольников называется тригонометрией. Вы не узнаете все, что вам нужно знать о треугольниках в 6-м классе, но вы сделаете хороший старт!
Площадь треугольника равна его основанию, умноженному на его высоту (5 х 4 = 20), разделенному пополам (20 ÷ 2 = 10). Вы увидите эту формулу, записанную как A = ½ bh .
Графики — отличный способ визуализации и сравнения чисел. Гистограммы (или диаграммы) являются одним из наиболее распространенных типов.
Сначала мы смотрим на ось Y (вертикальную), чтобы найти то, что нам сказали искать: круговые диаграммы. Затем мы перемещаемся по оси X (горизонтальной), чтобы увидеть, где заканчивается полоса: 2. Это означает, что было два случая, когда люди говорили: «мой любимый график — круговой».
Среднее значение группы чисел иногда называют «средним».
Среднее значение вычисляется путем сложения чисел в наборе (5 + 3 + 6 + 2 = 16) и деления этого ответа на количество элементов в наборе (16 ÷ 4 = 4).
Чтобы разделить дроби, нужно умножить обратное число. Не волнуйтесь, это не так сложно, как кажется!
Умножьте числитель или верхнее число первой дроби (4) на знаменатель или нижнее число второй дроби (2), чтобы получить числитель ответа (4 x 2 = 8). Далее умножьте знаменатель первой дроби (5) на числитель второй дроби (1), чтобы получить знаменатель ответа (5 х 1 = 5). Затем упростите 8/5 до 1⅗.
Абсолютные значения обычно записываются между ||, поэтому вы также можете написать этот вопрос как |-8| знак равно
Абсолютное значение любого числа, положительного или отрицательного, всегда положительное. Вы можете думать об этом как о расстоянии от нуля на числовой прямой. И 8, и -8 имеют одинаковое абсолютное значение 8, так как они оба отстоят от нуля на 8 целых чисел.
А чтобы узнать больше о способах отточить свой ум, начните с 50 лучших продуктов для вашего мозга.
Этот процесс называется объединением одинаковых терминов.
Пока числа объединяются с одной и той же переменной (в данном случае a ), вы можете складывать, вычитать, умножать или делить их, как если бы переменной не было. Вы даже можете думать о переменной как о физическом объекте. Если у вас есть 4 яблока, и я дам вам еще 2 яблока, сколько яблок у вас сейчас?
Параллелограмм представляет собой четырехстороннюю фигуру, состоящую из двух пар параллельных прямых.
Площадь параллелограмма можно найти, умножив его основание на высоту. Эту формулу также можно записать в виде A = bh , поэтому 5 x 4 = 20.
В математике число в верхнем индексе является показателем степени, а это означает, что для получения ответа потребуется повторное умножение.
Показатель степени говорит вам, сколько раз нужно умножить базовое число само на себя, чтобы получить полное число.
Он обычно используется для упрощения длинных чисел, поскольку, например, с 10⁹ гораздо проще работать, чем с 1 000 000 000 (девять нулей).
Вам нужно знать, как найти множители любого заданного числа, а затем сравнить их.
Делители числа 36 равны 1, 2, 3, 4, 6, 9, 12, 18 и 36. Делители числа 12 равны 1, 2, 3, 4, 6 и 12. общим является 12.
Коробчатая диаграмма — это график, который позволяет показать разброс и форму данных. «Данные» — это просто красивое слово для набора чисел, часто чисел, которые соответствуют результатам опроса или эксперимента.
Прямоугольник на диаграмме показывает средние 50% диапазона чисел. Внутри этого прямоугольника находится линия, определяющая медиану или значение, которое окажется прямо посередине, если вы выстроите все числа в ряд от меньшего к большему. Например, средние 50 % диапазона 2, 3, 6 и 8 будут равны 3–6, а медиана — 4,5. На приведенной выше блочной диаграмме линия медианы появляется между 8 и 10 примерно на уровне 8,5.
Умножать и делить десятичные числа не так сложно, если убрать десятичную дробь… но не забудьте вернуть ее обратно!
Сначала представим, что 1,92 — это целое число: 192 с двумя знаками после запятой. Затем разделите 192 на 3, чтобы получить 64. Теперь верните два десятичных знака, чтобы получить окончательный ответ 0,64.
Знай свои десятки, сотни и тысячи, но не путай их с десятыми, сотыми и тысячными!
2 находится в столбце сотен, а следующее число справа (столбец десятков) — 9, что означает, что вам нужно округлить.
Этот тип графика называется гистограммой, но вы можете использовать те же термины для описания точечных диаграмм, гистограмм и коробчатых диаграмм.
Поскольку форма, которую создают эти данные, (приблизительно) одинакова по обе стороны от центральной оси (в данном случае нулевая точка на оси X), она симметрична. Поскольку он достигает своего наивысшего пика по оси Y в середине, мы говорим, что он имеет форму колокола.
У вас останется несколько дюймов.
В футе 12 дюймов, поэтому 272 разделить на 12 будет 22 с остатком 8.
Множители и множители тесно связаны между собой.
Наименьшее общее кратное (иногда сокращенно НОК) — это наименьшее число, которое делится на два (или более) рассматриваемых целых числа. Таким образом, 208 — это наименьшее число, которое можно разделить без остатка как на 16 (208 ÷ 16 = 13), так и на 26 (208 ÷ 26 = 8).
Площадь поверхности – это сумма площадей всех фигур, составляющих внешнюю сторону трехмерной фигуры.
Прямоугольные формы, такие как картонные коробки, имеют 6 внешних сторон: верхнюю и нижнюю, переднюю и заднюю, левую и правую. Формула для расчета этой площади поверхности: (длина х ширина) х 2 + (длина х высота) х 2 + (высота х ширина) х 2. Здесь это означает (4 х 3) х 2 = 24, (4 х 7) х 2 = 56 и (7 х 3) х 2 = 42. Сложите их вместе: 24 + 56 + 42 = 122 дюйма².
Чтобы складывать или вычитать дроби, они должны иметь одинаковый знаменатель.
Во-первых, вы должны найти наименьший общий знаменатель или наименьшее число, которое делится на оба нижних числа дробей. Для 12 и 5 это число равно 60. Затем вы должны преобразовать каждый числитель. Так как вам нужно умножить 12 на 5, чтобы получить 60, умножьте 7 на 5, чтобы получить 35/60. Так как вам нужно умножить 5 на 12, чтобы получить 60, умножьте 2 на 12, чтобы получить 24/60. Теперь их можно сложить: 35/60 + 24/60 = 59./60. Вы не можете дальше упрощать 59/60, так что это ваш ответ!
Важно уметь наносить точки на координатную плоскость. Вас также могут попросить найти площадь фигур на координатной сетке.
Первое число в паре — это положение на оси X (горизонтальной); второе число — это положение на оси Y (вертикальной). Ваша сетка должна выглядеть так, как показано выше.
Объем фигуры — это количество вещей, которые могут поместиться внутри нее. Двумерные формы, такие как квадраты, не имеют объема, но трехмерные формы, такие как кубы, имеют.
Объем любой прямоугольной коробки можно найти, умножив длину на ширину на высоту . Поскольку все ребра куба имеют одинаковую длину, 10 х 10 х 10 = 1000.
Пи — постоянное число, а не вкусный десерт! Знайте, как использовать число пи (π) для вычисления площади или окружности круга.
Найдите длину окружности, умножив число пи (π = 3,14) на диаметр (7,7 фута).
В этой задаче вам нужно преобразовать возраст в смешанные числа и вычесть их.
Чтобы вычесть смешанные числа, преобразуйте их в неправильные дроби и выполните ту же процедуру, что и для сложения и вычитания дробей. Поскольку три месяца составляют ¼ года, а шесть месяцев — ½ года, задача решается как 9¼ – 2 ½. Преобразуйте оба числа в четверти, так что 9 ¼ = 37/4 и 2 ½ = 10/4. 37/4 – 10/4 = 27/4. Упростите 27/4 до 6¾. Три четверти года — это девять месяцев, поэтому ответ — 6 лет и 9.месяцы.
Так же, как укус превращает человека в зомби, вы превращаете эти числа в дроби!
Соотношение говорит нам, что на каждые 2 зомби приходится 3 человека, что дает нам группу из 5 (2 + 3) человек.
Разделите общее количество (85) на группы по 5, получив 17 групп. Умножьте их на исходные передаточные числа, чтобы получилось (17 х 2) 34 зомби и (17 х 3) 51 человек.
Чтобы узнать больше удивительных секретов о том, как прожить свою лучшую жизнь, нажмите здесь , чтобы подписаться на нашу БЕСПЛАТНУЮ ежедневную рассылку новостей!
Общий базовый экзамен по математике для 6-го класса (примеры вопросов)
Общий базовый экзамен по математике для 6-го класса с практическими вопросами
1. Население Нью-Йорка примерно вдвое превышает население Парижа. Напишите отношение населения Нью-Йорка к населению Парижа.- 1:1
- 1:2
- 2:½
- 2:1
- 10
- 16
- 20
- 25
- 16
- 24
- 48
- 96
Остаток на вашем сберегательном счете равен -50, что означает, что у вас есть 50 долларов долга. Ежемесячная плата увеличивает сумму вашего долга. Что из следующего может быть вашим новым балансом? - 60
- 40
- -40
- -60
- 2
- 3
- 6
- 8
- 2
- 3
- 4
- 8
- 9
- 10
- 15
- 20
- 4
- 8
- 12
- 16
82, 94, 81, 70, 72, 78, 95, 83, 89, 80, 55, 77
Создайте гистограмму для отображения данных.
- дней
- долларов
- человек
- шоу
1. D: Отношение — это отношение между двумя числами одного типа. Например, если соотношение яблок и апельсинов в корзине 3:2, то на каждые 2 апельсина в корзине приходится 3 яблока. В данной задаче ищем соотношение между населением двух городов. Поскольку нам говорят, что население Нью-Йорка примерно в два раза превышает население Парижа, на каждого парижанина приходится примерно два жителя Нью-Йорка. Поэтому правильное соотношение 2:1.
2. C: Процент представляет одну часть из 100. Таким образом, 40% эквивалентно 40 частям из 100, или 40/100.
Чтобы найти 40% от 50, умножьте 40/100 на 50:
40/100 X 50 = 20
3. B: кратное обоим числам. Один из способов найти НОК 8 и 12 — составить список их кратных чисел и выбрать наименьшее число из обоих списков.
8: 8, 16, 24, 32, 40, 48
12: 12, 24, 36, 48, 60, 72
Поскольку 24 — наименьшее число в обоих списках, НОК 8 и 12 равно 24.
4. D: Увеличение суммы долг означает, что вы должны более 50 долларов. Если, например, ваш долг увеличивается на 10 долларов, он становится 60 долларов, а баланс вашего счета становится -60. Таким образом, -60 может быть вашим новым балансом. (Обратите внимание, что остаток, равный -40, означает, что вы должны 40 долларов США, что уменьшит ваш долг.)
5. C: В соответствии с порядком операций (PEMDAS) сначала оцените любые количества или выражения в скобках. . Вычтите, чтобы найти значение в скобках, а затем разделите 24 на результат этого вычитания:
24 x (6 – 2) = 24 ÷ 4 = 6
6.
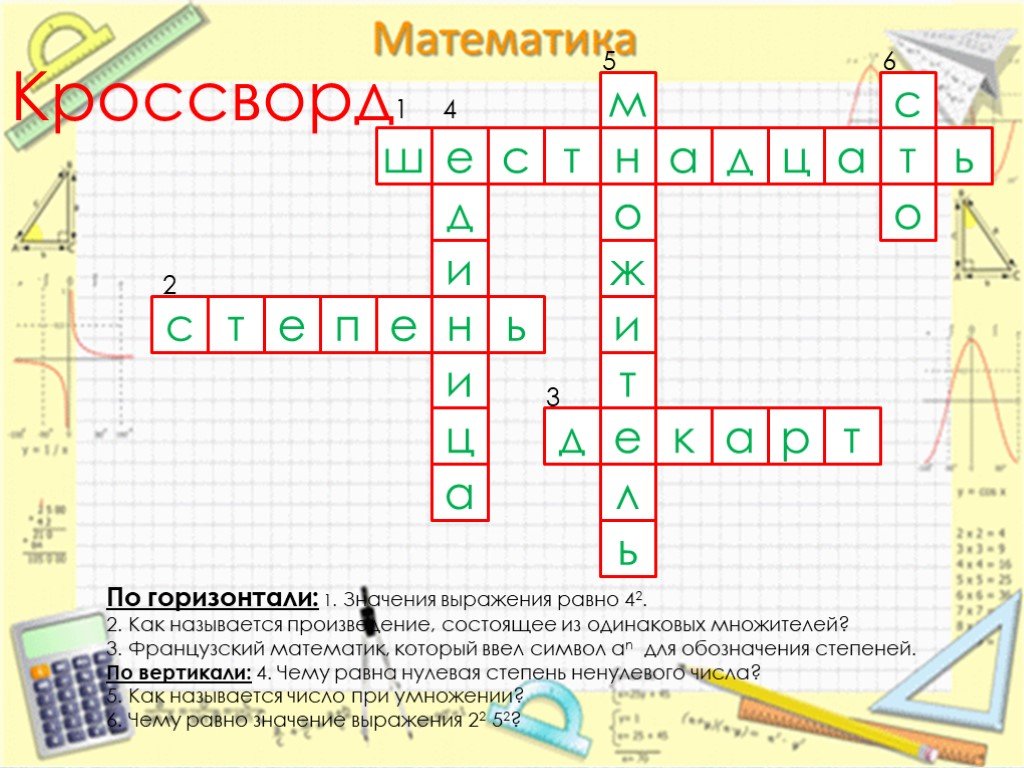A:
9 + 2x > 5x
9 + 2(2) > 5(2)
9 + 4 > 10
13 > 10
Поскольку верно 13 > 10, правильный ответ x = 2.
В качестве альтернативы вычтите 2x из обеих частей неравенства, чтобы получить 9 > 5x – 2x, что эквивалентно 9 > 3x. Разделите обе части на 3, чтобы получить 3 > x или x < 3. Единственное значение x, которое меньше 3, равно 2, поэтому верно A.
7. B: Площадь треугольника определяется по формуле A = ½ bh , где b основание треугольника, а h высота треугольника (начерчена линией перпендикулярно основанию). Поскольку треугольник является прямоугольным, вы можете использовать горизонтальную сторону для основания и вертикальную сторону для высоты:
A = ½ bh
= ½ (4)(5)
= ½ (20)
= 10
8.
A: Среднее значение набора данных — это его среднее значение. Следовательно, если все значения в наборе не равны 12 (а вы знаете, что это не так, потому что диапазон равен 8), некоторые из них должны быть меньше 12, а некоторые должны быть больше 12.
Диапазон набора данных это разница между его наибольшим и наименьшим значениями. Поскольку диапазон этого набора равен 8, все значения в наборе должны быть больше 4. Если одно значение равно 4, должно быть значение больше 12, чтобы среднее значение оставалось равным 12, а разница между этим значением и 4 будет больше, чем 8. Поскольку мы знаем, что диапазон равен 8, 4 не может быть значением в наборе.
9. A:
Гистограмма — это способ графического представления распределения набора данных. В гистограмме диапазон данных разделен на интервалы, так что каждое значение попадает в один интервал. Для заданных результатов теста естественным способом установить интервалы являются 50–59, 60–69, 70–79, 80–89 и 90–100.