Состав Числа Примеры Тренировки Хитрости в Мышлении
Для чего нужно знать состав числа?
Как упражнения по составу чисел могут помочь вашему ребенку , Какая польза от знания состава числа.
Ответы на эти вопросы Вы можете получить у нас на сайте.
С составом числом знакомиться уже начинают в детском саду, в старших группах есть занятия по подготовке детей к школе. Малышей учат считать и решать простенькие примеры и задачи.
А для этого детям дают задание запомнить состав числа.
В возрасте 6-7 лет ребенка знакомят с составом чисел от 0 до 10 . Изучение состава числа поможет будущему школьнику легко освоить сложение и вычитание.
К этому возрасту ребенок знает наизусть прямой счет до 10, обратный счет в пределах 10, умеет пересчитывать и отсчитывать предметы, знает состав числа из единиц: понимает, что 3 — это 1 и 1 и 1. Все это говорит о том, что ваш ребенок готов к изучению состава чисел до 10 из двух меньших чисел.
Состав числа начинают изучать с опорой на наглядный материал.
Когда мы просто складываем разные числа, результат может получиться любой. Но когда мы выясняем состав какого-то числа, то как бы идём в обратном направлении — от результата, который известен заранее. Мы учим определённые пары слагаемых — у каждого числа они свои, — чтобы получался именно этот результат.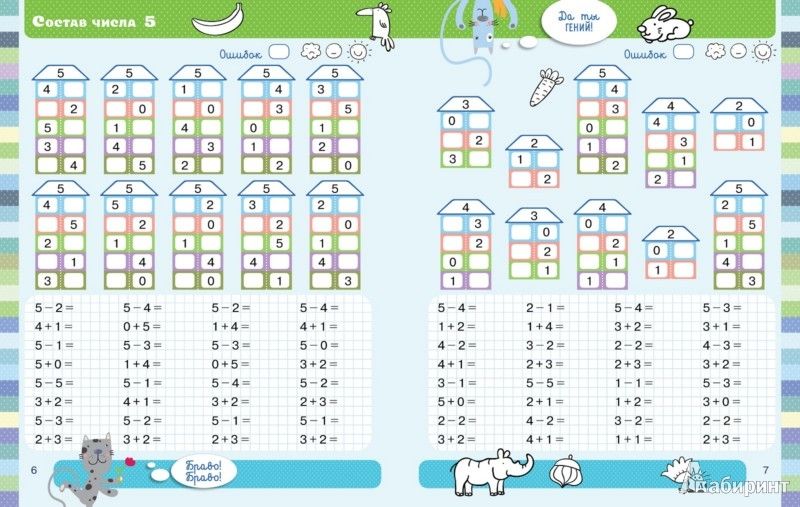
Помните
Знание состава числа — залог быстрого счета, устного и письменного. Если во время подготовки к школе состав числа до 10 не уложился у ребенка в голове, надо обязательно уделить этому время в первом классе, а потом не забывать о закреплении состава числа до 20 и далее — это сильно сократит время на вычисления.
Я предлагаю действовать в таком порядке.
- Объяснить наглядно, как при одной и той же сумме одно слагаемое может увеличиваться, а второе — уменьшаться. Очень удобно это делать на предметах, которых всегда фиксированное и привычное глазу количество: отлично подходят коробки из-под яиц (10), прозрачные упаковки печенья или конфет (обычно 6, 8, 12), строчки календаря (7), упаковки акварели, пластилина и т.п.
- Ребёнок обязательно должен записать в тетрадь (или на листочек) все возможные варианты состава числа, проговорить их вслух, найти и соединить примеры с одинаковыми слагаемыми (7+1 и 1+7, например) если он конечно может писать.

- Очень советую сделать для закрепления состава числа карточки вида
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
Отдельную карточку на каждый пример. Зачем? Карточки составом числа дают нам много возможностей для заучивания комбинаций.
Обзаведитесь карточками на состав числа. Их можно купить или сделать. Они бывают нескольких типов, и лучше, чтобы они были двух видов. Разрезная карточка состоит из двух половинок. На одной изображён 1 предмет, на другой — 1, 2, 3 и больше точно таких же предметов. Половинки могут быть соединены знаком «+», но «плюс» можно сделать и отдельно. Второй комплект представляет собой набор картинок, на которых изображены эти же предметы одним множеством, без всякого разделения. Когда ребёнок хорошо научится сопоставлять число и цифру, можно сделать такие же карточки с цифрами. Их может быть несколько комплектов, чтобы представлять каждое число в разных вариантах.
Проводите занятия регулярно. Покажите ребёнку карточку, на которой изображено, скажем, 5 предметов.
Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.
Аналогичные задания поводите и с цифрами. Покажите, например, число 9 и точно так же, как в предыдущем случае, предложите найти несколько вариантов его состава. Объясните ребёнку, что чем больше число — тем больше возможностей его составить.
Например:
- Раскладываем карточки по порядку.
- Просим ребёнка все их назвать.
- Переворачиваем, кладём карточки лицевой стороной вниз.
- Просим ребёнка их припомнить.
- Открываем, проверяем, хвалим!
Сделать столько раз, сколько понадобится, чтобы ребёнок назвал их все. Заниматься можно буквально по нескольку минут, между делом.
Поговорим о хитростях запоминания
Расскажите, что любое число всегда состоит из единицы и предыдущего числа. Таким образом, если нужно определить состав числа 8, у ребенка уже готов один ответ: 8 – это 1 и 7. Соответственно, чтобы определить, сколько будет 8 минус 1, нужно от 8 отчитать 1 в обратном порядке, то есть назвать предыдущее число.
Таким образом, если нужно определить состав числа 8, у ребенка уже готов один ответ: 8 – это 1 и 7. Соответственно, чтобы определить, сколько будет 8 минус 1, нужно от 8 отчитать 1 в обратном порядке, то есть назвать предыдущее число.
Познакомьте ребенка также с отсчетом 2. Чтобы ответить на вопрос: 8 – это 2 и сколько?, нужно сначала отсчитать 1 в обратном порядке, а потом еще 1.
Больше практикиЧтобы довести определение состава числа до автоматизма, решайте как можно больше примеров. Можно играть в игру: вы называете число, состав которого нужно определить, ребенок как можно быстрее показывает любое уместное количество пальцев, вы показываете оставшееся количество. Потом меняетесь ролями. Эта игра также тренирует навык сравнения, ведь если вы назовете 4, ребенку нельзя показать 5 и более пальцев.
Это интересно, читайте также:
Изучаем Состав Числа в виде Игры
Тренировка
А теперь будем тренировать запоминание. Точнее, припоминание. Теперь наши задания направлены на то, чтобы ребёнок припоминал нужные примеры.
Точнее, припоминание. Теперь наши задания направлены на то, чтобы ребёнок припоминал нужные примеры.
Задание 1. Я делаю так — даю листок с примерами, где есть и те примеры, которые мы сейчас учим, и другие. Инструкция для ребёнка: «Найди все примеры, которые мы сейчас учили, и запиши правильный ответ. На другие примеры сейчас не обращай внимания».
(Некоторые прилежные дети начинают всё равно решать все примеры. Поэтому я стараюсь подбирать такие «ненужные» примеры, которые они должны были уже освоить.)
Самое главное — наблюдать за ребёнком в процесс работы: он припоминает примеры (те, которые мы сейчас заучиваем) или заново считает? Если считает — ничего не получилось! Либо ребёнок их ещё не запомнил (тогда надо вернуться к пункту 3), либо не понимает, чего мы сейчас от него хотим. Нам нужно именно это: найти знакомые примеры!
Задание надо выполнить хотя бы 3- раза (не сразу, с интервалами, в один день не более двух раз через промежуток времени).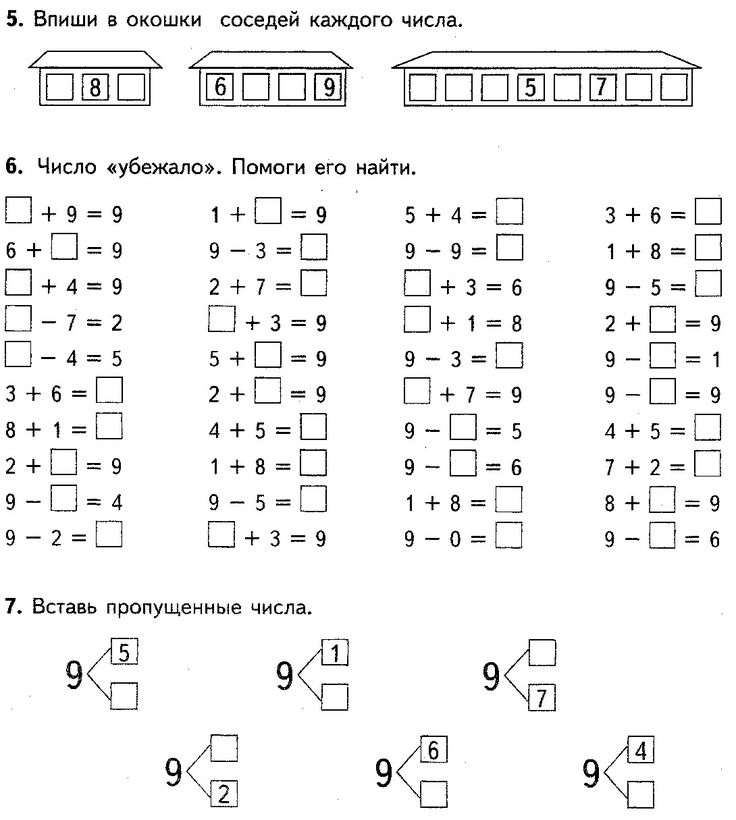
Задание 2. Снова даём ребёнку листок с примерами, где есть и те, которые мы «учили», и на состав других чисел. И просто просим решать примеры. Не подсказываем, что некоторые примеры он уже «помнит».
Наблюдаем. Делаем выводы: если вспоминает «наши» примеры и сразу пишет в них ответы — ура, получилось! Если нет — возвращаемся к пункту 3.
Примеры с вычитанием
Теперь нас ждёт непростой момент — мы должны научить ребёнка решать примеры на вычитание, используя знание состава числа.
Если мы помогаем первокласснику, необходимо использовать математические термины: «Когда мы складываем два слагаемых, у нас получается сумма. Это примеры на сложение. А что такое пример на вычитание? Это когда мы знаем сумму и знаем одно слагаемое, а второе слагаемое не знаем. Как его найти? Для этого из суммы мы вычитаем известное слагаемое.
Но если ты помнишь состав числа, то неизвестное слагаемое ты можешь просто припомнить. Мы с тобой выучили состав числа 8. Ты помнишь все комбинации? Перечисли!»
Ты помнишь все комбинации? Перечисли!»
Ребёнок отвечает:
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
«Молодец! А теперь давай будем менять числа местами! Наши примеры будут на вычитание, поэтому сумму 8 мы всегда будем ставить на первое место. Вычитать можно только из самого большого числа! Вычитать будем одно из слагаемых, а второе будет получаться в ответе. Давай попробуем: называй любой пример на сложение с ответом 8!»
5 + 3 = 8
«Сейчас мы с тобой будем „прятать“ одно слагаемое, делать его неизвестным. Что у нас получится:
8 — 5 = ?
Правильно, 3! Второе слагаемое!
Давай попробуем ещё раз:
6 + 2 = 8
А сколько будет:
8 — 6 = ?
Правильно, 2 — второе слагаемое!».
На этом этапе я даю детям вот такие примеры:
6 + 2 =
2 + 6 =
8 — 2 =
8 — 6 =
5 + 3 =
3 + 5 =
8 — 3 =
8 — 5 =
Такая последовательность примеров помогает ребёнку осознать связь сложения и вычитания. И опять же — всё направлено на запоминание.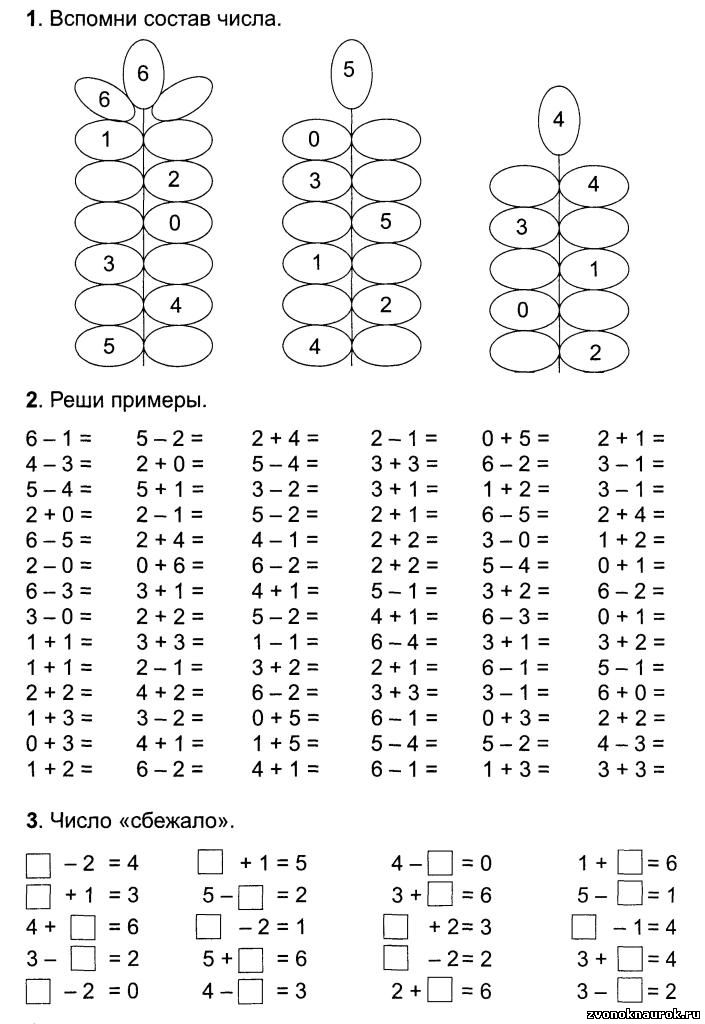 Когда мы решаем примеры на вычитание, можно посчитать, а можно припомнить. Припоминать — быстрее!
Когда мы решаем примеры на вычитание, можно посчитать, а можно припомнить. Припоминать — быстрее!
Момент связи сложения и вычитания очень важен для решения уравнений. Если ребёнок не улавливает эту связь, ему будет трудно решать уравнения.
Заполни пустые места или запоминанием состав числа
Скажем, 5 это 1 плюс 4, или 2 плюс 3, или 3 плюс 2, или 4 плюс 1.
Малыши заучивают это как стишок или скороговорку, зачастую просто не вникая или не понимая смысла.
Для того, чтобы состав чисел от 1 до 10 действительно отложился в детских головках, Ментальная Арифметика предлагает скачать карточки-задания на состав числа.
Для того, чтобы заполнить пустые места надо подумать. Раздумья ускоряют память детей и соответственно мысль.
Желаем Вам успехов в познании математических цифр.
Авторская статья от Аллы Ромашкиной
Ваш сайт Ментальная Арифметика.
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Учим состав числа — К школе готов!
Содержание
- Что такое состав числа и зачем его учить?
- Когда начинать учить состав числа
- Учим состав числа правильно
- Правило 1.
 Демонстрируйте разнообразный наглядный материал
Демонстрируйте разнообразный наглядный материал - Правило 2. Используйте активные действия самого ребенка
- Правило 3. Постепенно переходите от конкретных предметов к абстрактным числам и действиям в уме
- Этапы изучения состава числа
- Передвигаем предметы
- Заполняем домики
- Упражнения на закрепление состава числа
Что такое состав числа и зачем его учить?
Состава числа лежит в основе решения примеров на сложение и вычитание. Поэтому нужно четко понимать, что это такое и как с ребенком выучить состав числа. В этой статья расскажу, как мы с детьми учим состав числа.
Состав числа – это все варианты слагаемых, в виде которых можно представить это число. Например, 5 это 1 и 4, 2 и 3, 3 и 2, 4 и 1.
Знать состав чисел это значить уметь назвать такие пары для каждого числа от 1 до 10.
Но состав числа не ограничивается суммой только двух слагаемых. Ребенок должен понимать, что число 5 можно представить из трех, четырех и пяти чисел.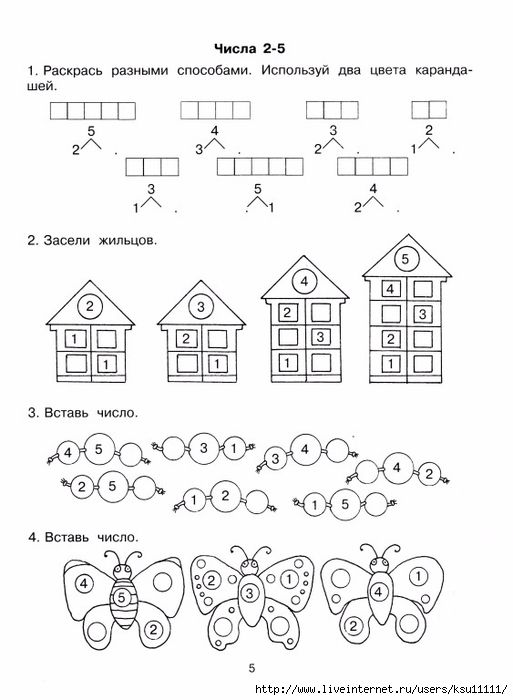 (5=2+2+1, 5=1+1+1+1+1)
(5=2+2+1, 5=1+1+1+1+1)
Когда начинать учить состав числа
В математике, как и в другой, науке все взаимосвязано. Поэтому, чтобы начать изучать состав чисел у ребенка уже должна быть сформирована начальная база знаний. Малыш должен уже знать цифры, понимать какое число каждая цифра обозначает, уметь считать до 10 в прямом и обратном порядке.
Если ребенок еще не уверенно считает, путает цифры, переходить к изучению состава числа еще рано. Продолжайте закреплять навыки счета. В этом вам поможет статья «Как научить ребенка считать?»
Учим состав числа правильно
Ваш ребенок свободно считает предметы до 10, называет предметы, значит можно переходить к изучению состава числа. Чтобы ребенок легко и быстро выучил состав числа, придерживайтесь трех важных правил:
Правило 1. Демонстрируйте разнообразный наглядный материал
Нельзя ограничиваться только счетными палочками. Можно использовать пуговицы, карандаши, реальные яблоки или их изображения.
Счетный материал не должен отвлекать внимание ребенка от главного. Поэтому картинки выбирайте не слишком яркие, без лишних деталей.
Все счетные элементы должны быть одинаковыми. Например, если это пуговицы, то пуговицы из одного набора, а не те, которые нашли у бабушки в коробке. Тогда внимание ребенка не будет рассеиваться на несущественные признаки: размер, цвет пуговиц, а сосредоточится на количественной характеристике множества – на числе.
Правило 2. Используйте активные действия самого ребенка
На первых этапах обучения составу числа давайте ребёнку больше заданий, в которых он перекладывает, добавляет, убирает предметы. Во время таких манипуляций ребенок наглядно видит взаимоотношения между числами. На основе конкретных образов формируются абстрактные математические представления.
Правило 3. Постепенно переходите от конкретных предметов к абстрактным числам и действиям в уме
Многократные повторения действий с конкретными предметами приведут к тому, что ребенок легко запомнит состав числа. Для этого не потребуется заучивание.
Для этого не потребуется заучивание.
На этом этапе ребенку уже не нужны счетные палочки. Все операции он совершает в уме. Можно переходить к выполнению действий с абстрактными числами.
Этапы изучения состава числа
Передвигаем предметы
На первом этапе ребенку нужно показать, что целое число можно представить в виде частей по-разному.
Лучше всего это сделать так. Рассмотрим на примере числа 5.
Выкладывает на столе 5 предметов для счета, в моем случае 5 яблок. Вместе с ребенком пересчитываем: всего 5 яблок. Затем, по одному отодвигаем яблоки в сторону и называем пары чисел. «5 это 1 и 4, 2 и 3, 3 и 2, 4 и 1» Ребенок наглядно видит, количество яблок не изменяется. Изменяются числа в парах. Причем, если слева на одно яблоко становится больше, то справа на одно яблоко становится меньше.
Заполняем домики
Домики — это классическое упражнение на закрепление состава числа. Рисуем домик с количеством этажей равным количеству пар. Для числа 5 этажей будет 4. На крыше домика пишем число 5, чтобы оно всегда было перед глазами ребенка. В окошках слева напишем цифры от 1 до 4. Для каждого числа ребенок называет пару, чтобы в сумме было 5.
На крыше домика пишем число 5, чтобы оно всегда было перед глазами ребенка. В окошках слева напишем цифры от 1 до 4. Для каждого числа ребенок называет пару, чтобы в сумме было 5.
Вариантов работы с домиками много:
- Можно придумать сказку про бездомных котят. Их нужно заселить их в домик так, чтобы на каждом этаже получилось 5 котят.
- Можно слева прописывать числа по порядку, затем в разброс.
- В домике окошки могут быть пустыми, тогда ребенок будет прописывать числа парами.
Упражнения на закрепление состава числа
Таких упражнений придумано много. Расскажу об одном, которое очень нравится детям. Я называю это упражнение «Фокусник».
Выкладываю на столе 5 предметов. Предлагаю детям пересчитать и запомнить количество предметов. Затем накрываю предметы салфеткой. Произношу магические слова: «Крибля, крабля, бумс!»
Открываю салфетку, при этом удерживаю рукой несколько предметов под салфеткой.
Удивленные дети видят, что несколько предметов пропало.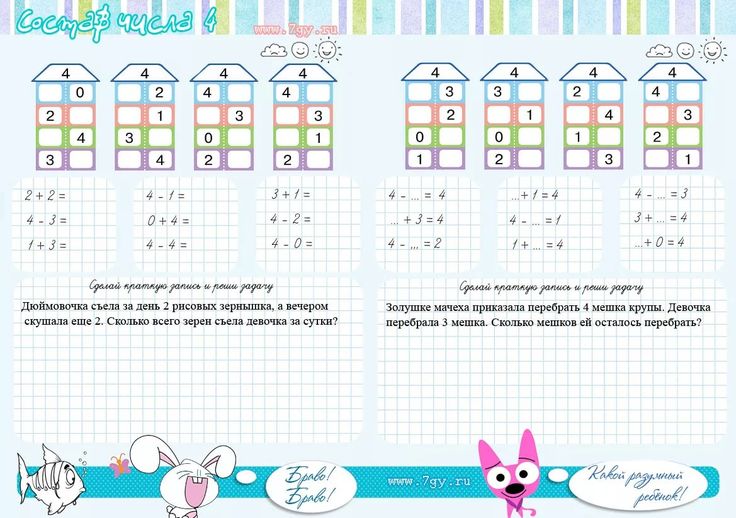
— Сколько предметов осталось?- спрашиваю (3)
— А сколько пропало? (2)
— Правильно, 3 и 2 будет 5.
В доказательство показываю те два предмета, которые спрятала.
Когда мы учим состав числа важно запастись терпением. Ребенку нужны многократное выполнение действий с предметами. Только так можно сформировать прочные абстрактные математические понятия.
Так в игровой форме, на основе действий с предметами, образного восприятия можно легко и естественно сформировать абстрактное понятие состава чисел. Теперь переходим к закреплению знаний при помощи упражнений в тетради.
Программа Python для суммы квадратов первых n натуральных чисел
Улучшить статью
Сохранить статью
Нравится Статья
- Уровень сложности: Easy
- Последнее обновление: 03 апр, 2023
Улучшить статью
Сохранить статью
Нравится Статья
Дано натуральное число N .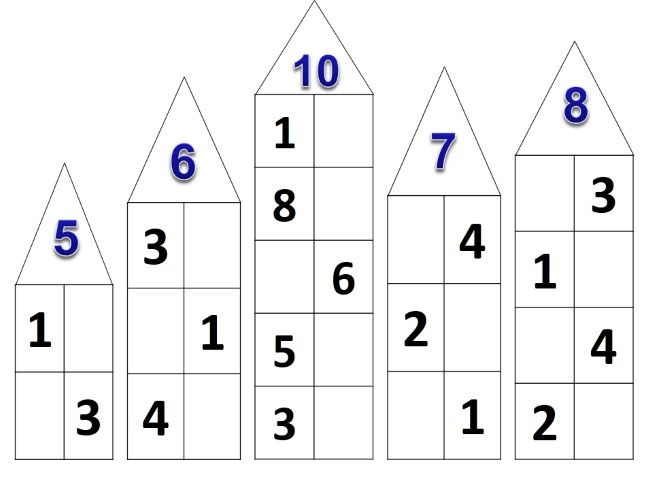 Задача найти 1 2 + 2 2 + 3 2 + ….. + N 2 .
Задача найти 1 2 + 2 2 + 3 2 + ….. + N 2 .
Примеры:
Ввод: N = 4 Выход : 30 1 2 + 2 2 + 3 2 + 4 2 = 1 + 4 + 9 + 16 = 30 Ввод: N = 5 Вывод: 55
Метод 1: O(N) Идея состоит в том, чтобы запустить цикл от 1 до n и для каждого i, 1 <= i <= n, найти i 2 в сумме.
питон3
для i в диапазоне ( 1 , n + 1 ):0003
|
Output
30
Method 2: O(1)
Доказательство:
Мы знаем, (k + 1) 3 = k 3 + 3 * k 2 + 3 * k + 1 Мы можем записать приведенное выше тождество для k от 1 до n: 2 3 = 1 3 + 3 * 1 2 + 3 * 1 + 1 ........ (1) 3 3 = 2 3 + 3 * 2 2 + 3 * 2 + 1 ........ (2) 4 3 = 3 3 + 3 * 3 2 + 3 * 3 + 1 ......... (3) 5 3 = 4 3 + 3 * 4 2 + 3 * 4 + 1 ........ (4) ... п 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 ......... (n - 1) (n + 1) 3 = n 3 + 3 * n 2 + 3 * n + 1......... (n) Помещая уравнение (n - 1) в уравнение n, (n + 1) 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 + 3 * n 2 + 3 * n + 1 = (n - 1) 3 + 3 * (n 2 + (n - 1)
2 ) + 3 * (n + (n - 1)) + 1 + 1 Составляя все уравнения, получаем (п + 1) 3 = 1 3 + 3 * Σ k 2 + 3 * Σ k + Σ 1 n 3 + 3 * n 2 + 3 * n + 1 = 1 + 3 * Σ k 2 + 3 * (n * (n + 1))/2 + n n 3 + 3 * n 2 + 3 * n = 3 * Σ k 2 + 3 * (n * (n + 1))/2 + n n 3 + 3 * n 2 + 2 * n - 3 * (n * (n + 1))/2 = 3 * Σ k 2 n * (n 2 + 3 * n + 2) - 3 * (n * (n + 1))/2 = 3 * Σ k 2 n * (n + 1) * (n + 2) - 3 * (n * (n + 1))/2 = 3 * Σ k 2 n * (n + 1) * (n + 2 - 3/2) = 3 * Σ k 2 n * (n + 1) * (2 * n + 1)/2 = 3 * Σ k 2 n * (n + 1) * (2 * n + 1)/6 = Σ k 2
python3
|
Выход
30
Сложность O (1)
Auxilarial: O (1) . 0028 Для больших n значение (n * (n + 1) * (2 * n + 1)) будет переполнено. We can avoid overflow up to some extent using the fact that n*(n+1) must be divisible by 2.
0028 Для больших n значение (n * (n + 1) * (2 * n + 1)) будет переполнено. We can avoid overflow up to some extent using the fact that n*(n+1) must be divisible by 2.
Python3
|
Выход
30,0
Сложность времени : O (1) Потому что конституционные операции выполняются 9037 AOVS : O (1). Потому что конституционные операции выполняются 9037 70027 70027 AOVIARIARIARITIOR AOVIARIARIARIARIARIARIER 770028 : O(1)
Потому что конституционные операции выполняются 9037 70027 70027 AOVIARIARIARITIOR AOVIARIARIARIARIARIARIER 770028 : O(1)
Подход: понимание списка
- Принимать ввод от пользователя в виде положительного целого числа N с помощью функции input().
- Преобразуйте входную строку в целое число с помощью функции int() и сохраните ее в переменной N.
- Используйте генератор списка для создания списка квадратов чисел от 1 до N. Генератор списка должен выглядеть следующим образом: [i*i для i в диапазоне (1, N+1)]. Это создает список квадратов чисел от 1 до N.
- Используйте функцию sum(), чтобы найти сумму всех элементов в списке. Сохраните результат в переменной sum_of_squares.
- Распечатайте результат с помощью функции print().
Python3
|
Результат
Сумма квадратов первых 5 натуральных чисел равна 55Подход: итеративный
Мы можем использовать цикл для перебора первых n натуральных чисел и вычисления суммы их квадратов.

Шаги:
- Инициализировать сумму переменных значением 0.
- Использовать цикл для перебора первых n натуральных чисел, т. е. от 1 до n.
- В цикле вычислите квадрат текущего числа и добавьте его к сумме.
- После завершения цикла выведите значение sum.
Python3
| |
Output
Сумма квадратов первых 4 натуральных чисел равна 30
Временная сложность: O(n)
Подробнее см. полную статью о сумме квадратов первых n натуральных чисел. !
полную статью о сумме квадратов первых n натуральных чисел. !
Нравится статья
Сохранить статью
Что такое номер вызова?
Когда вы ищете печатную книгу или другой физический предмет в библиотеке, чаще всего вам понадобится телефонный номер, чтобы найти его в наших коллекциях.
Библиотечный каталог будет включать некоторые основные сведения о местоположении (например, «Коллекция учебных программ W.A.C. Bennett Library (Burnaby)»), а также телефонный номер для этих физических предметов.
Всем печатным или бумажным копиям книг в библиотеке присваивается телефонный номер, обычно указанный на корешке книги.
Номер вызова показывает, о чем книга, и действует как адрес книги на полках или в стопках библиотеки. Поскольку книги на полках расставлены в порядке телефонного номера, вы найдете книги по схожим темам на полках рядом друг с другом.
В библиотеке SFU используется система классификации Библиотеки Конгресса (LC). Номера вызовов LC состоят из букв и цифр и выглядят примерно так:
PR 8923 W6 L36 1990 c.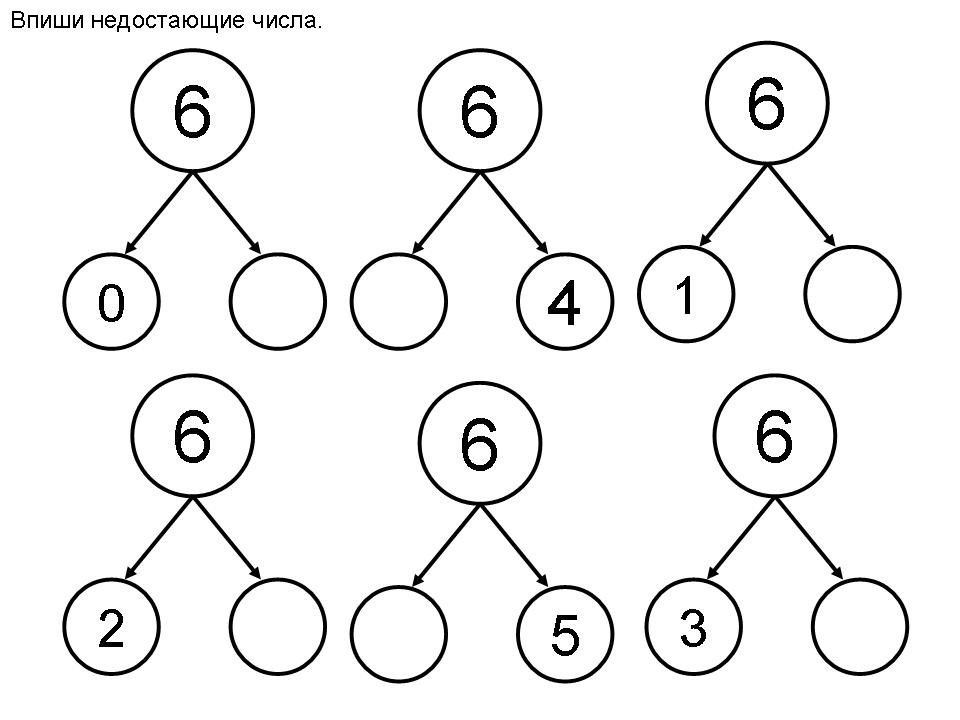 3
3
Читать номер вызова слева направо. Первая часть номера вызова, PR 8923 , состоит из комбинации одной или двух букв и цифры, указывающей на конкретную предметную область.
Следующая часть, W6 L36 , идентифицирует конкретное название среди книг по этой теме, 1990 — дату публикации, а c.3 указывает, что это третья копия в библиотеке. .
Если у вас есть телефонный номер для вашей книги (или другого предмета), вы можете использовать ссылку на план этажа в записи каталога книги, чтобы увидеть область библиотеки, где вы можете найти книгу.
Или проверьте эти карты библиотеки SFU, чтобы найти местоположение.
- Начните с нахождения первой буквы вашего телефонного номера. В приведенном выше примере телефонные номера, начинающиеся с буквы P, находятся на 5-м этаже W.A.C. Библиотека Беннета в Бернаби.
- Номера вызова, начинающиеся с одной буквы, идут перед номерами вызова со второй буквой, например: P перед PA, затем PB, PC и так далее до PR.


 Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.
Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.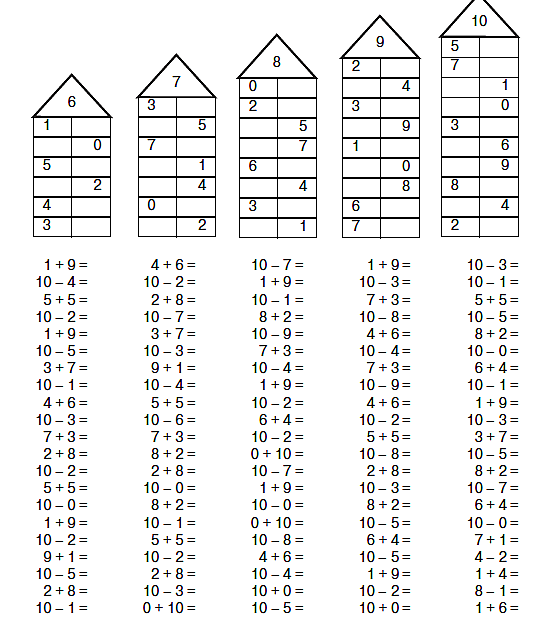 Демонстрируйте разнообразный наглядный материал
Демонстрируйте разнообразный наглядный материал ....... (1)
3 3 = 2 3 + 3 * 2 2 + 3 * 2 + 1 ........ (2)
4 3 = 3 3 + 3 * 3 2 + 3 * 3 + 1 ......... (3)
5 3 = 4 3 + 3 * 4 2 + 3 * 4 + 1 ........ (4)
...
п 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 ......... (n - 1)
(n + 1) 3 = n 3 + 3 * n 2 + 3 * n + 1......... (n)
Помещая уравнение (n - 1) в уравнение n,
(n + 1) 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 + 3 * n 2 + 3 * n + 1
= (n - 1) 3 + 3 * (n 2 + (n - 1)
....... (1)
3 3 = 2 3 + 3 * 2 2 + 3 * 2 + 1 ........ (2)
4 3 = 3 3 + 3 * 3 2 + 3 * 3 + 1 ......... (3)
5 3 = 4 3 + 3 * 4 2 + 3 * 4 + 1 ........ (4)
...
п 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 ......... (n - 1)
(n + 1) 3 = n 3 + 3 * n 2 + 3 * n + 1......... (n)
Помещая уравнение (n - 1) в уравнение n,
(n + 1) 3 = (n - 1) 3 + 3 * (n - 1) 2 + 3 * (n - 1) + 1 + 3 * n 2 + 3 * n + 1
= (n - 1) 3 + 3 * (n 2 + (n - 1)