Закон умножения дробей: 133, 134. Законы умножения дробей

Умножение дробей.Законы умножения

Дорогу осилит идущий, математику – мыслящий

«Счет и вычисления – основа порядка в голове» Песталоцци И

• Как умножить на 5,15, 25 и на 11
• 2405 = ; 96 5 = ; 32 5 = ;
• 18 15 = ; 44 15 = ; 26 15 = .
• 16 25 = ; 8 25 = ; 24 25 = .
• 26 ∙ 11 = ; 43∙11 = ; 84 ∙11 = ;
• 18 ∙ 11 = ; 47 ∙11 = .

•  

1) 308 • 4

2) половина 2500

3) ( 3964 + 378 ) – 2964

4) 64056 : 8

5) 25 • 27 • 4

6) 6060 • 100

7) 6536 + 3464

8) 3807 – 3007

9) 4596 – ( 550 + 596)

10) 20100 — 1

Помогите Винни — Пуху

Самопроверка:

Винни– Пух и яблоки

• Винни–Пух пошёл в гости к Пятачку. Пятачок поставил на стол две тарелки с яблоками. В одной тарелке – 3 целых яблока, а в другой -5 половинок.
• “ Выбирай,” – говорит Пятачок.
• Винни–Пух любит хорошо поесть. Ему захотелось выбрать тарелку, в которой яблок побольше, но он никак не может понять , что больше: 3 целых яблок или 5 половинок.
• Помогите Винни – Пуху выбрать нужную тарелку

Запишите дробью, какая часть фигуры, изображённой на рисунке , заштрихована

в)

б)

а)

д)

е)

г)

Решение упражнений

30

• Найдите от числа 120

• Найдите от числа 120

• Найдите число, если

от него равно 35?

80

• Найдите число, если

от него равно 20?

36

63

Задача

На столе лежат 18 шариков. Одна вторая — синие, одна третья – жёлтые, остальные – зеленые.

Сколько шариков каждого цвета?

1.Как умножить две дроби? ( произведение двух дробей есть дробь , числитель которой равен произведению числителей , а знаменатель – произведению знаменателей этих дробей: )

 

2.Как умножить натуральное число на дробь? (чтобы умножить натуральное число на дробь , можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же = )

3.Какую дробь называют обратной? (дробь называют обратной для дроби ( ).

4.Какие дроби называются взаимно обратными?

(дроби и называют взаимно обратными дробями ( числами))

5.Чему равно произведение взаимно обратных чисел? (произведение взаимно обратных чисел равно 1 )

6.Сформулируйте и запишите переместительный закон умножения (от перестановки множителей произведение не меняется )

 

7. Сформулируйте и запишите сочетательный закон умножения (чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел ) = )).

8. Сформулируйте и запишите распределительный закон умножения относительно сложения ( чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить + = + )

9. Сформулируйте и запишите распределительный закон умножения относительно вычитания

( чтобы число умножить на разность двух чисел, можно это число умножить на уменьшаемое и вычитаемое и от первого произведения вычесть второе произведение, и если — = — )

1 . Если произведение чисел равно______, то такие числа называют взаимно простыми.

А) 0; В) 1; С) натуральному числу.

2. Чтобы умножить обыкновенную дробь на _____________, надо числитель этой дроби умножить на это число, а знаменатель оставить тот же.

А) натуральное число; В)смешанное число; С) обратное число.

3. Чтобы найти дробь от числа, надо это число умножить на ______________.

А) 1; В) обратную ей дробь; С) данную дробь.

4.Запишите алгоритм умножения обыкновенных дробей.

Чтобы умножить обыкновенные дроби,надо:

1. Числитель первой дроби умножить на ____________________ ,

2. _____________________ умножить на знаменатель второй,

3. если можно ____________________,

4. выполнить _________________ в числителе и в знаменателе

5. Запишите это правило на математическом языке (формулой).

5. Запишите переместительный закон умножения

6. Запишите сочетательный закон умножения

7.Запишите распределительный закон умножения относительно сложения

8. Запишите распределительный закон умножения относительно вычитания

. Если произведение чисел равно ___1___ , то такие числа называют взаимно простыми.

 

А) 0; В) 1; С) натуральному числу.

2. Чтобы умножить обыкновенную дробь на _натуральное_ надо числитель этой дроби умножить на это число, а знаменатель оставить тот же.

А) натуральное число; В)смешанное число; С) обратное число.

3. Чтобы найти дробь от числа, надо это число умножить на

_данную дробь__

А) умножить на 1; В) на обратную ей дробь; С) на данную дробь.

4.Запишите алгоритм умножения обыкновенных дробей.

Чтобы умножить обыкновенные дроби надо:

1. Числитель первой дроби умножить на _числитель второй _

2. _знаменатель первой _ умножить на знаменатель второй,

3. если можно _сократить числитель и знаменатель на общий делитель

4. выполнить __умножение_ в числителе и в знаменателе

5. Запишите это правило на математическом языке (формулой)

6.

7. ) = ).

8 + = +

9. если , то — = —

Творческое задание :

Как разрезать головку сыра на 8 равных частей, выполнив всего лишь три разреза

18 слайд

Решение :

19 слайд

2

8

4

части

частей

16

Великий русский писатель Л.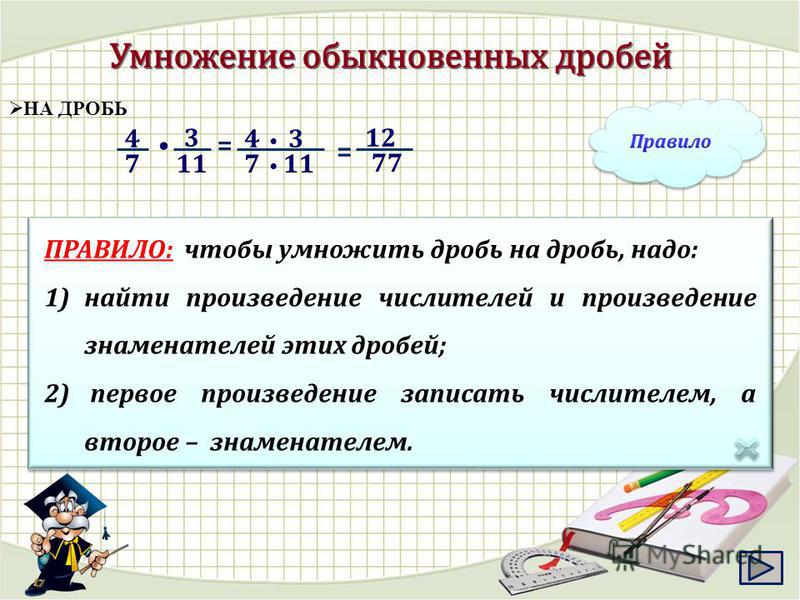 Н.Толстой писал, что человека можно оценивать дробью, знаменатель которой составляет то хорошее, что думает о себе человек, а числитель – то хорошее, что думают о нём другие люди. А как вы считаете? Правильно ли это ?

Успехов Вам, дорогие ребята и уважаемые коллеги , и, дай вам Бог, мудрости научиться заботиться о своём здоровье и здоровье своих учеников , потому что счастья человека — это здоровье .

 

Математика, 6 класс: 13-18. Умножение десятичных дробей

13-18. Умножение десятичных дробей

Устный счет

Это надо знать

Умножение десятичной дроби на 10; 100; 1000 и так далее

При умножении десятичной дроби на 10; 100; 1000 и так далее запятую надо перенести вправо на столько знаков, сколько нулей в числе на которое умножаем.

Примеры: 

5,13 ∙ 10 = 51,3

1,235 ∙ 100 = 123,5

0,56 ∙ 1000 = 560

---

Умножение десятичной дроби на 0,1; 0,01; 0,001 и так далее

При умножении десятичной дроби на 0,1; 0,01; 0,001и так далее запятую надо перенести влево на столько знаков, сколько цифр после запятой в числе на которое умножаем.

Примеры: 

5,13 ∙ 0,1 =  0,513

123,5 ∙ 0,01 = 1,235

0,56 ∙ 0,001 = 0,00056

---

Умножение десятичных дробей

1. Перемножить десятичные дроби как натуральные числа, не обращая внимание на запятые;

2. В полученном произведении отделить запятой справа столько десятичных знаков, сколько их содержится  в обоих множителях вместе;

3. Отбросить нули в конце дробной части (если они есть).

Пример: 

5,25 ∙ 0,4  =  2,1 

---

Законы умножения

Переместительный закон умножения

a ∙ b = b ∙ a

Сочетательный закон умножения

a ∙  (b ∙ c) = (a ∙  b)  ∙ c

Распределительный закон умножения

a ∙  (b  + c) = a ∙  b  +  a ∙ c

a ∙  (b  — c) = a ∙  b  —  a ∙ c

Видеоурок

Домашнее задание

К уроку 13 (на 20.09)

П. 3.1

1 уровень (учебник)

№  3.3

№  3.7

---

2 уровень (сборник)

№ 1.41 стр. 11
Найдите произведение 1,20689 и числа:

1) 10;                   2) 1000;                          3) 10 000; 4) 100; 

5) 100 000;          6) 100 000 000;              7) 1 000 000 000; 

8) 1 000 000;       9) 10 000 000 000.

№ 1.44 стр. 12

На какое число была умножена десятичная дробь 17, 29, если в результате получилось число:

1) 1 729 000;     2) 1 729 000 000;      3) 172 900 000 000?

№ 5. 18 стр. 120

Периметр треугольника равен 14,4 дм. Длина одной из его сторон на 1 дм больше длины другой и на 1,6 дм меньше третьей стороны. Найдите длины сторон треугольника.

   

К уроку 14 (на 21.09)

П. 3.2

1 уровень (учебник)

№  3.18

№  3.20

---

2 уровень (сборник)

№ 1.45 стр. 12
На какое число была умножена десятичная дробь 916,1, если в результате получилось число:
1) 0,09161; 2) 0,9161; 3) 0,0009161?

№ 1.47 стр. 13
Найдите произведение 804 и десятичной дроби:
1) 0,001;           2) 0,01;         3) 0,000001;            4) 0,1;             5) 0,0001;            6) 0,00000001.

№ 5.19 стр. 121

Сумма двух чисел равна 124. При делении большего числа на меньшее получается в частном 3 и в остатке 4. Найдите эти числа.

   

К уроку 15 (на 22.09)

П. 3.3

1 уровень (учебник)

№  3.31

№  3.35

---

2 уровень (сборник)

№ 1.56 стр. 14
Найдите произведение чисел:
1) 4,8 ∙ 12,9;         2) 90,8 ∙ 0,15;            3) 62,07 ∙ 2,48.
№ 1.60 стр. 15
Используя верное равенство 612 ∙ 78 = 47 736, найдите значение выражения:

1) 6,12 ∙ 7,8;         2) 0,612 ∙ 7,8;           3) 0,0612 ∙ 0,78;               4) 0,00612 ∙ 7,8;

5) 0,000612 ∙ 0,078;              6) 0,00612 ∙ 0,00078.

№ 5.4 стр. 118
Во время ремонта планируется выложить кафельной плиткой пол на кухне. Для этого куплено 150 штук кафельной плитки для пола размером 25 см на 25 см каждая. Хватит ли этой плитки, чтобы выстелить пол на кухне площадью 9,35 м²

   

К уроку 16 (на 23. 09)

П. 3.3

1 уровень (учебник)

№  3.37 (1-4)

№  3.39

---

2 уровень (сборник)

№ 1.59 стр. 15

Вычислите:
1) 1,23 ∙ 5,7;         2) 0,43 ∙ 4,91;           3) 15,74 ∙ 0,035;               4) 7,64 ∙ 22,3;

5) 0,0801 ∙  14,35;              6) 9,041 ∙ 0,0042.

№ 5.48 стр. 126
Два комбайна, работая вместе, могут выполнить задание за 6 часов. Первый комбайн, работая один, может выполнить задание за 10 часов. За сколько часов может выполнить это задание второй комбайн, работая один?

  

К уроку 17 (на 26.09)

П. 3.3

1 уровень (учебник)

№  3.53 (1-4)

№  3.55

---

2 уровень (сборник)

№ 1. 63 стр. 15
Найдите 0,15 от числа:

1) 23;            2) 8;              3) 4,2;                   4) 0,76;                      5) 105,22;               6) 6045,38.

№ 5.58 стр. 127

На одну чашу весов положили кусок хозяйственного мыла, на другую — 0,6 такого же куска и, чтобы уравновесить весы, гири массой 0,6 кг. Найдите массу одного куска хозяйственного мыла.

   

К уроку 18 (на 27.09)

П. 3.4

1 уровень (учебник)

№  3.63

№  3.73 (1-4)

---

2 уровень (сборник)

№ 1.58 стр. 14
Выполните действия:
1) 6,482 ∙ 10  ∙  3,05;       2) 0,001 ∙ 4,28  ∙ 35;     3) 5,094 ∙ 100  ∙ 0,401;     4) 10 000 ∙ 0,0519  ∙ 0,034.

№ 5.60 стр. 128
На вопрос, сколько у него учеников, Пифагор ответил: «Половина моих учеников изучает математику, четверть — изучает природу, восьмая часть — проводит время в молчаливом размышлении, остальную часть составляют три девы». Сколько учеников было у Пифагора?

   

Подписаться на: Сообщения (Atom)

Умножение дробей — Math28

Contenido

Что такое умножение дробей?

Умножение дробей — одна из основных операций, позволяющая получить третью дробь, которая будет произведением предыдущих, что известно как «Произведение» или «Результат умножения».

Узнать больше о: » Умножение » →

Символ или знак умножения дробей

Умножение дробей представлено символом креста или «х», оно также может быть представлено с помощью средней точки, символ умножения известен как «на».

Узнать больше о: » Операции с дробями » →

---

Как мы умножаем дроби?

Для получения числового значения в виде дробей существует только одна процедура умножения дробей либо с разными знаменателями, либо с одинаковыми знаменателями.

При умножении дробей числители дробей умножаются, а знаменатели расходятся.

2 / 2

х

1 / 2

=

2 / 4

2/2

1/2

2/4

В следующем примере дроби 1/3 и 2/6 перемножаются, определяются числители обеих дробей, соответствующие 1 и 2, перемножаются и результат помещается в числитель. Теперь определите знаменатели обеих дробей, соответствующие 3 и 6, умножьте и поместите результат в знаменатель.

1 / 3

х

2 / 6

=

1 х 2 / 3 х 6

=

2 / 18

Результат 2/18 можно упростить, потому что и числитель, и знаменатель можно уменьшить вдвое. Таким образом, половина от 2 равна 1, а половина от 18 равна 9.

2 / 18

=

1 / 9

Примечание : Дроби 2/18 и 1/9 эквивалентны, поскольку они представляют одну и ту же сумму.

Пример:

2 / 3

х

4 / 3

=

2 х 4 /

3 х 3

=

8 / 9

5 / 2

х

6 / 2

=

5 х 6 /

2 х 2

=

30 /

4

5 / 6

х

4 / 3

=

5 х 4 /

6 х 3

=

20 /

18

8 / 3

х

2 / 4

=

8 х 2 /

3 х 4

=

16 /

12

Из предыдущих примеров можно упростить 30/4 = 15/2, 20/18 = 10/9 и 16/12 = 4/3.

Упражнение:

А)

5 / 3

х

3 / 3

= ?

Б)

9 / 2

х

5 / 2

= ?

С)

6 / 5

х

4 / 3

= ?

Д)

6 / 8

х

2 / 2

= ?

---

Умножение трех и более дробей

Процедура похожа на две дроби, умножение выполняется в строке, числитель на числитель и знаменатель на знаменатель.

4 / 2

х

5 / 3

х

3 / 2

=

4 х 5 х 3 / 2 х 3 х 2

=

60 / 12

=

10 /

2

= 5

Пример:

3 / 2

х

4 / 2

х

8 /

2

=

3 х 4 х 8 /

2 х 2 х 2

=

96 /

8

3 / 4

х

5 / 4

х

10 /

4

=

3 х 5 х 10 /

4 х 4 х 4

=

150 /

64

2 / 3

х

4 / 2

х

4 /

6

=

2 х 4 х 4 /

3 х 2 х 6

=

32 /

36

5 / 4

х

4 / 8

х

3 /

2

=

5 х 4 х 3 /

4 х 8 х 2

=

60 /

64

Из предыдущих примеров можно упростить 96/8 = 12, 32/36 = 8/9 и 60/64 = 15/18.

Упражнение:

А)

4 / 3

х

7 / 2

х

3 / 2

= ?

Б)

4 / 2

х

5 / 2

х

3 / 4

= ?

С)

3 / 2

х

7 / 2

х

3 / 2

= ?

Д)

6 / 6

х

7 / 6

х

2 / 6

= ?

---

Умножение смешанных дробей

При умножении смешанных дробей необходимо, чтобы вся часть выражалась в виде дроби, имеющей тот же знаменатель, что и в сопровождающей ее дробной части. Например, чтобы выполнить следующее смешанное умножение:

4

2 / 5

х 3

4 / 8

1.- Вся часть умножается на знаменатель прилежащей дроби. 4 х 5 = 20 3 х 8 = 24

2.- К результату умножения добавляется числитель соответствующей дроби.

20 + 2 /

5

х

24 + 4 /

8

3.- После преобразования смешанных дробей можно выполнить умножение.

22 /

5

х

28 /

8

=

22 х 28 /

5 х 8

=

616 /

40

Узнать больше о: « Смешанные фракции » →

арифметика — Объяснение умножения дробей

спросил 8 лет, 2 месяца назад

Изменено 8 лет, 2 месяца назад

Просмотрено 1к раз

9а_{я=1} б$$ Но мое определение не учитывает такие вещи, как $2,99792458\times8,987551787$ и $\frac{1}{7}\times\frac{2}{9}$ Когда дело доходит до дробей и десятичных знаков, я не могу объяснить это интуитивно.

Согласно Википедии, для дробей

Обобщение дробей $\frac{A}{B}\times \frac{C}{D}$ осуществляется путем умножения числителей и знаменателей соответственно: $\frac{A}{B}\times \frac{C}{ D} = \frac{(A\times C)}{(B\times D)}$. Это дает площадь прямоугольника $\frac{A}{B}$ в высоту и $\frac{C}{D}$ в ширину, и это то же самое, что количество элементов в массиве, когда рациональные числа оказываются целые числа.

Есть ли более интуитивный способ выражения произведения двух дробей, чем что-то столь расплывчатое, как площадь прямоугольника? (по крайней мере мне кажется туманным)

• арифметика
• интуиция
• образование
• бинарные операции

$\endgroup$

3

$\begingroup$

Я буду говорить с исторической точки зрения в защиту умножения как соответствующего площади.

Человеческие культуры не развили символического понимания умножения в течение довольно долгого времени (возможно, даже у древних греков, хотя я могу ошибаться). Самые ранние зарегистрированные свидетельства, демонстрирующие человеческое знание умножения, показывают, что умножение сначала понималось геометрически: величина, которую мы теперь назвали бы $a\times b$, определялась как площадь прямоугольника высотой $a$ и шириной $b. $ всем ранним цивилизациям, знавшим об этом понятии, включая месопотамцев (включая вавилонян) и египтян.

Исходя из этого, мы можем утверждать, что площадь прямоугольника является наиболее интуитивным способом понять умножение. Удобный аспект этого определения заключается в том, что оно универсально для всех систем счисления, являющихся подмножеством действительных чисел. Как только фиксируется единица длины, возникает соответствие между любым действительным числом и конкретной длиной (хотя определение может быть громоздким для иррациональных чисел), и, таким образом, для любых двух действительных чисел $a$ и $b$ прямоугольник высоты $a$ и ширины $b$ определяется интуитивно. В частности, очень легко определить геометрически длину, соответствующую дроби $a/b$, поэтому этот подход очень естественно подходит для рациональных чисел, и именно так древние культуры понимали умножение дробей. Эта универсальность в определении является преимуществом, которого лишена концепция целочисленного умножения как «повторяющегося сложения».

Позже, конечно, люди развили алгебраическое понимание умножения и обобщили его на более абстрактные алгебраические структуры; с определенной точки зрения можно попытаться понять умножение как своего рода алгебраический формализм, но опять же это не столько «попытка понять», сколько «решение не беспокоить».

$\endgroup$

$\begingroup$

Если принять, скажем, что $3\times 7$ равно $3$ группам по $7$, то можно перейти к определенным типам дробей, умноженных на целые числа. Например, $\frac23 \times 12$ — это $\frac23$ группы из $12$. Поскольку одна треть от 12 долларов составляет 4 доллара, две трети от 12 долларов составляют две четверки или 8 долларов.

Мы также могли бы решить задачу, подобную $\frac23 \times \frac{12}{17}$, поняв, что $\frac{12}{17}$ — это $12$ элементов (каждый элемент равен одной семнадцатой части целого ). Поскольку $\frac23$ из $12$ элементов равно $8$, мы получаем, что $\frac23\times \frac{12}{17}=\frac8{17}$.

Если значения несовместимы, мы можем использовать эквивалентные дроби. Например, предположим, что мы хотим сделать $\frac23\times \frac57$. Перепишем $\frac57$ так, чтобы числитель можно было взять по трети. То есть $$\frac23\times\frac57=\frac23\times \frac{15}{21}.$$ Но $\frac13$ из пятнадцати двадцать первых равно пяти двадцать первым. Итак, две трети от пятнадцати двадцать первых составляют две группы по пять двадцать первых, то есть десять двадцать первых.

Мы утверждали, что $$\frac23\times\frac57=\frac{10}{21}.$$ Подобным образом можно решить и другие задачи на умножение дробей.

$\endgroup$

1

$\begingroup$

Историческая причина, по которой умножение определяется таким образом, заключается в том, как раньше интерпретировалось умножение, когда речь шла о дробях. Если у вас есть прямоугольный блок квадратов и есть $6$ квадратов в поперечнике с $8$ квадратом вверху, вы бы сказали, что ваш прямоугольный блок состоит из $6\x 8$ квадратов. В некотором смысле умножение измеряет «площадь» единицей квадратов.

Теперь, если вы вводите дроби, вы по-прежнему можете интерпретировать умножение как своего рода площадь. Допустим, что по горизонтали есть квадраты $\tfrac{3}{2}$, а по вертикали — квадраты $\tfrac{5}{3}$. Нам нужно найти площадь такого квадрата. Чтобы представить это вычисление, лучше всего ввести общие знаменатели и разбить каждую единичную сторону на $\tfrac{1}{6}$ того, что было. Теперь на горизонтальной стороне $9$ шестых квадратов, а на вертикальной стороне $10$ шестых квадратов.