Запишите распределительный закон для целых чисел а, b, c, сформулируйте его.
Все вопросы /Математика / класс
0 /10000
Ответы2
Распределительный закон умножения относительно сложения
Рассмотрим распределительный закон умножения относительно сложения.
- Для любых целых чисел а, b, c справедливо равенство (a + b) · с= a · с + b · с.
- Чтение равенства (a + b) · с= a · с + b · с: произведение суммы чисел а и b на число с равно сумме произведений а на с и b на с.
- Рабочая формулировка: для того, чтобы умножить сумму на число, достаточно, каждое слагаемое умножить на число и полученные результаты сложить.
В школе изучаются: свойство умножения суммы на число и свойство умножения числа на сумму.
Свойство умножения суммы на число.
Умножить сумму на число можно разными способами:
- 1 способ: (4+3) ∙ 2 = 7 ∙ 2 = 14; можно вычислить сумму и полученный результат умножить на число;
- 2 способ: (4+3) ∙ 2 = 4 ∙ 2 + 3 ∙ 2 = 8 + 6 = 14; можно каждое слагаемое умножить на число и полученные результаты сложить.
Свойство умножения числа на сумму.
Умножить число на сумму можно разными способами:
- 1 способ. 16∙(2+3)=16∙5=80; вычислить сумму и число умножить на полученный результат;
- 2 способ. 16∙(2+3)=16∙2+16∙3=80; умножить число на каждое слагаемое и полученные произведения сложить.
Распределительный закон умножения относительно вычитания
Рассмотрим распределительный закон умножения относительно вычитания.
- Для любых целых чисел а, b, c справедливо равенство (a — b) · с= a · с — b · с.
- Чтение равенства (a — b) · с= a · с — b · с: произведение разности чисел а и b на число с равно разноси произведений а на с и b на с.
- Рабочая формулировка: для того, чтобы умножить разность на число, достаточно, уменьшаемое умножить на число, вычитаемое умножить на число и найти разность полученных результатов.
- Хотя этот закон можно рассматривать и как распределительный закон умножения относительно сложения (a + (- b)) · с= a · с + (- b) · с = a · с — b · с.
Умножение разности на число: 99 · 3 = (100 — 1) ·3 = 100 · 3 — 1 · 3 = 300 – 3 = 297;
умножение числа на разность 247 · 98 = 247 · (100 — 2) = 247 · 100 — 247 · 2 = 24 700 — 494 = 24 206.
Существует распределительный закон относительно сложения и вычитания.
Сформулируем распределительный закон относительно сложения для целых чисел а, b, c:
чтобы сумму чисел а и b умножить на число с, можно умножить на число с каждое слагаемое, то есть числа а и b и сложить полученные произведения ((а + b) * с = а * с + b * с).
Сформулируем распределительный закон относительно вычитания для целых чисел а, b, c:
чтобы разность чисел а и b умножить на число с, можно умножить на число с уменьшаемое и вычитаемое отдельно и из первого произведения вычесть второе ((а — b) * с = а * с — b * с).
Законы сложения кратко (6 класс, математика)
Средняя оценка: 4.6
Всего получено оценок: 292.
4.6
Средняя оценка: 4.6
Всего получено оценок: 292.
Законы сложения и умножения – это простейшие правила арифметики 6 класса. Это знание пригодится на всех этапах жизни человека, поэтому имеет смысл поговорить о каждом из них подробно.
Сложение
Сложение – это простейшее свойство математики. Суть сложения заключается в том, что количество единиц одного слагаемого и количество единиц другого слагаемого объединяются в одно число. Сложение и умножение очень близки по духу. Ведь умножение это сложение одного и того же числа несколько раз с самим собой.
Количество раз, которое необходимо сложить число обозначает второй множитель. Первый множитель это то число, которое мы складываем.
Переместительное
«От перемены мест слагаемых сумма не меняется». В этом и заключается переместительное свойство сложения.
Мы можем решить пример таким образом:
7+15=22 – и это будет верно. Но что изменится от того, что мы запишем пример: 15+7 и решим его еще раз?
15+7=22 – как видите, результат не изменился.
Та же ситуация наблюдается и для умножения. От перемены мест множителей – произведение не изменится.
5*6=30, но и:
6*5=30
Это свойство умножения вытекает из схожести слоения и умножения. Нет разницы, сложить 5 раз 6 или 6 раз 5.
Сочетательное
Второе свойство называется сочетательным. При сложении трех чисел, нет разницы: сложить первые два слагаемых и прибавить к нему третье или наоборот: сложить последние два слагаемых и прибавить к ним первое.
Второе свойство проистекает из первого, расширяясь с двух слагаемых до трех. Разберемся подробнее. Представим сумму из трех слагаемых:
а+в+с=р
Согласно второму свойству нет разницы, выполнить сложение так:
(а+в)+с=р
Или так:
а+(в+с)=р
Скобки указывают на порядок выполнения действий.
Та же ситуация наблюдается и с умножением:
(а*в)*с=р
а*(в*с)=р – разницы нет. Результат от этого не изменится.
Свойство называется сочетательным, потому что нет разницы, как сочетать слагаемые в примере.
Распределительный закон умножения относительно сложения
Этот закон немного труднее, но и используется он чаще всего в буквенных выражениях. Он заключается в том, что если один из множителей это скобка с суммой, то можно посчитать сумму и умножить число на нее, а можно умножить число на каждое из слагаемых и посчитать уже их сумму:
а(в+с)=р
ав+ас=р
Что мы узнали?
Мы кратко поговорили о законах сложения и умножения. Узнали, почему каждое свойство имеет такое название, и поговорили о распределительном законе умножения относительно сложения.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Шварева Наталья
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 292.
А какая ваша оценка?
Умножение — произведение, закон, пример и законы
Умножение часто описывается как повторяющееся сложение .
Например, произведение 3 × 4 равно сумме 4 + 4 + 4 трех четверок. Закон, на котором это основано, — распределительный закон: a(b + c) = ab + ac. В этом случае закон применяется к 4(1 + 1 + 1), что дает 4(1) + 4(1) + 4(1) или 4 + 4 + 4.
Когда один или оба множителя не являются натуральными числами , закон все еще действует, 0,4 (1,2) = 0,4 (1) + 0,4 (0,1) + 0,4 (0,1), но члены суммы не просто «повторяются», и другие правила, такие как как правила для размещения десятичной точки, необходимы.
Конечно, никто не возвращается к закону распределения каждый раз, когда он или она вычисляет продукт. Фактически, большая часть времени в младших классах школы посвящена составлению таблицы умножения и ее запоминанию для последующего использования. Однако, применяя эту таблицу к таким продуктам, как 12 × 23, можно явно использовать закон распределения:
Здесь а равно 12; б равно 20; и с равно 3.
Говоря об умножении, используется несколько терминов. В 6 × 3 все выражение, независимо от того, записано ли оно как 6 × 3 или как 18, называется произведением.
Каждая из 6 и 3 называется множителями, факторами или иногда терминами. Старые слова «множимое» (для 6) и «множитель» (для 3), которые делали различие между числом, которое было умножено, и числом, которое произвело умножение, вышли из употребления. Теперь «множитель» применяется к любому числу.
Умножение обозначается тремя способами: знаком «×», как в 6 × 3; с точкой в центре, как в 6 • 3; и написав числа рядом друг с другом, например, 5x, 6 (3), (6) (3) или (x + y) (x — y). Последний способ обычно предпочтительнее.
| Для всех номеров a, b и c | |
| ab — уникальный номер | закон закрытия |
| аб = ба | коммутативный закон |
| а(бк) = (аб)в | ассоциативный закон |
| а•1 = а | закон мультипликативной идентичности |
| Если ab = cb и b ≠ | закон об отмене |
| Из этих законов можно вывести еще три полезных закона: | |
| а•0 = 0 | свойство умножения на ноль |
Если ab = 0, то a = 0, или b = 0, или и то, и другое. | отсутствие делителей нуля |
| Факторы продукта могут комбинироваться в любом порядке. | обобщенное коммутативное свойство |
Умножение подчиняется не только дистрибутивному закону, связывающему его со сложением, но и законам, применимым только к умножению. Эти законы представлены в таблице выше.
Поскольку арифметика выполняется с натуральными числами, необходимы некоторые дополнительные законы для работы с десятичными дробями, обыкновенными дробями и другими числами, которые не являются натуральными числами:
Десятичные дроби: умножайте десятичные дроби, как если бы они были натуральными числами. Поставьте запятую в произведении так, чтобы количество разрядов в произведении равнялось сумме разрядов в множителях. Например, 3,07 × 5,2 = 15,964.
Дроби: Числитель произведения равен произведению числителей; знаменатель произведения есть произведение знаменателей. Например, (3/7)(5/4) = 15/28.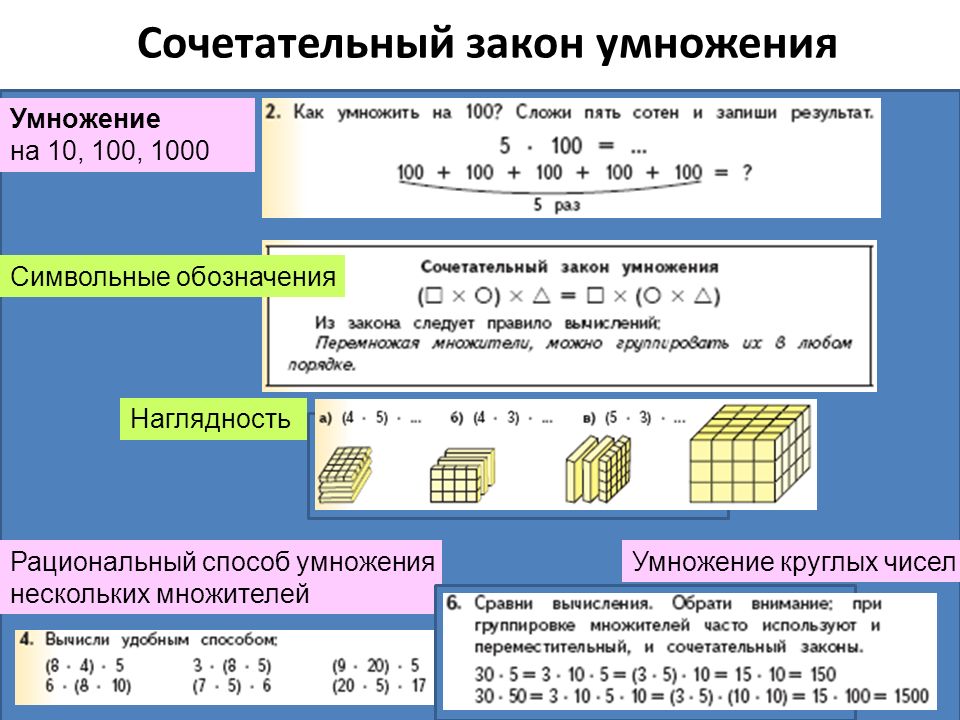
Числа со знаком: умножьте числа, как если бы они не имели знаков. Если один из двух множителей имеет знак минус, поставьте произведение со знаком минус. Если оба множителя имеют знак минус, произведение записывают без знака минус. Например, (3x)(-2y) = -6xy; (-5)(-4) = 20; (-х) 2 = х 2 ; и (5x)(x) = 5x 2 .
Степени одного основания: Чтобы умножить две степени одного и того же основания , сложите показатели степени. Например, 10 2 × 10 3 = 10
0.
Одночлены: Чтобы умножить два одночлена, переставьте множители. Например, (3x 2 y)(5xyz) = 15x 3 y 2 z.
Многочлены : Чтобы умножить два многочлена, умножьте каждый член одного на каждый член другого, комбинируя одинаковые члены.
Например, (x + y)(x — y) = x 2 — xy + xy — y 2 = x 2 — y
Умножение — это модель для множества практических ситуаций. В одном у нас есть число, а, групп с b вещами в каждой группа . Произведение ab представляет общее число. Например, семь коробок для яиц вмещают в общей сложности 7 × 12 яиц. В других ситуациях мы имеем «прямую вариацию» или пропорциональность: y = kx. Такое количество галлонов бензина при таком-то количестве на галлон требует умножения, как и вычисление расстояния как функции от скорости и времени, D = RT.
В отличие от сложения, при котором длина плюс длина есть другая длина, а длина плюс вес бессмысленны, произведение двух величин одного и того же типа или разных типов часто имеет смысл и имеет тип, отличный от обоих. Например, произведение двух одномерных мер, таких как длина, становится двумерной мерой площади.
Умножение сила , такая как сила тяжести, на расстоянии дает работу, которая представляет собой изменение количества энергии . Таким образом, в то время как умножение тесно связано со сложением в вычислительном отношении, в приложении оно учитывает отношения более сложных измерений.
Хотя умножение обычно является операцией между числами, оно также может быть операцией между другими видами математических элементов. Умножение в более широком смысле подчиняется многим законам обычного умножения, но не обязательно всем.
Например, в «часовой арифметике» выполняются все основные законы, кроме отмены. В часовой арифметике 3 × 4 = 3 × 8, потому что обе стрелки остаются в одном и том же положении, но, конечно, 4 не равно 8. При умножении матриц коммутативность не выполняется.
Особенно интересным расширением идеи умножения является декартово произведение двух множеств. Если A = {1, 2, 3} и B = {x, y}, то A × B — это множество {(1, x), (1, y), (2, x), (2, y ), (3, x), (3, y)}, образованный соединением каждого элемента A с каждым элементом B.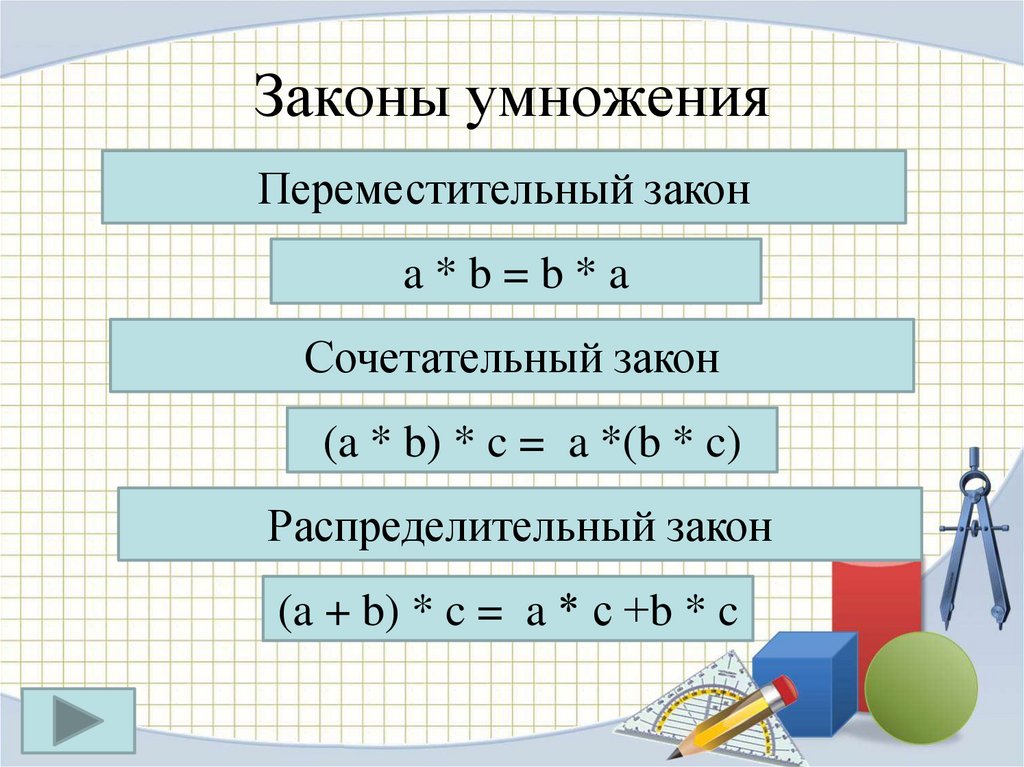
Поскольку множества иногда используются в качестве основы для арифметики, декартовы произведения образуют важную связь между множествами и обычным умножением .
Законы алгебры
Дом
Узнать
Алгебра
- Что такое алгебра
- Алгебра в повседневной жизни
- Основные алгебраические термины
- Методы решения по алгебре
- Линейные, нелинейные уравнения
- Алгебра Формулы
- Коммутативные Ассоциативные законы
- Формула расстояния
- Метод фольги
- Формула средней точки
- Скобки Правила
- Квадратное уравнение
- Квадратичная формула
- Полиномиальные операции
- Полиномиальное сложение
- Полиномиальное вычитание
- Полиномиальное умножение
- Многочлен длинного деления
- Графики полиномиальных функций
Пусть a,b,c — три переменные.
Далее приведены некоторые основные правила алгебры, применимые к этим переменным.
«а + b = b + а`
`а.б = ба`
` а + (b + c) = (a + b) + c ` ` а + (б + с) = (а + б) + с `
` а.(b.c) = (a.b).c ` ` а.(б.с) = (а.б).с `
` а.(б + в) = (а.б) + (а.в) ` ` а.(b + c) = (а.b) + (а.с) `
`a + c = b + c тогда и только тогда, когда a = b`
` a.c = b.ciffa = b`, где c != 0
В следующем разделе ,
мы используем эти простые формулы для решения поставленных задач.
Commutative Law for Addition Examples
Example 1:
Example 2:
Distributive Law Example
Associative Law Example
Cancellation law For Addition Example
Cancellation law For Multiplication Example
Распределительный закон Примеры
Распределительное свойство Примеры
Ассоциативное свойство для умножения Примеры
Здесь нужно упомянуть, что вычитание, деление, умножение матриц, векторное произведение некоммутативны.
Например:
`4-2!=2-4` => Вычитание не является коммутативным
«( 4 )/( 2 )!=2/( 4 )` => Деление не является коммутативный
Аналогичным образом можно показать, что умножение матриц и векторное произведение некоммутативны.