Засели числа в домики математика: Соседи числа «Домики» — задание для счета

Как объяснить ребенку состав числа?

Современная программа обучения в школе задает для будущих первоклассников достаточно высокую планку. Придя в школу, ребенок уже должен иметь определенный багаж знаний и навыков, одним из которых является понимание состава числа.

Состав числа – это возможность раскладывать числа от 1 до 10 на два меньших числа. Этот навык заложит фундамент, благодаря которому ребенку в будущем будет легче осваивать математику, например, сложение и вычитание. Если уделять время занятиям и постепенно осваивать эту тему, то результат не заставит себя ждать. А математические тренажеры помогут в усвоении новых знаний.

Чтобы ребенок мог успешно освоить эту тему, он уже должен узнавать графические образы цифр, уметь считать от 1 до 10 и, желательно, от 10 до 1 в обратном порядке. Также плюсом будет возможность самостоятельной записи ребенком цифр. Подходящий возраст для занятий по составу числа – от 6 лет, но иногда можно начинать изучать состав небольших чисел и раньше.

Все зависит от индивидуальных особенностей и базы знаний, которыми он владеет.

Состав числа в пределах 10

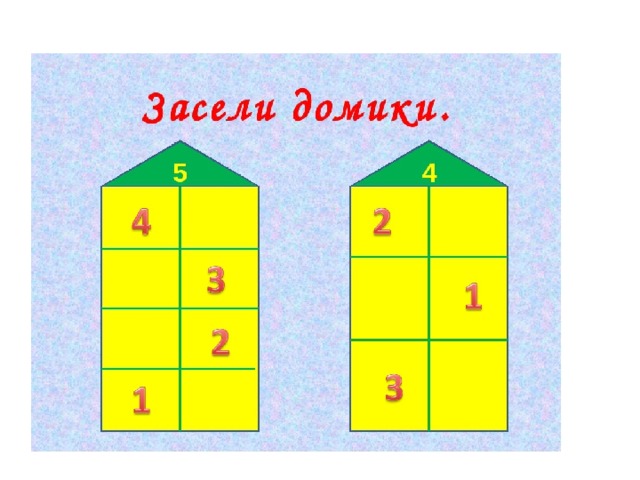
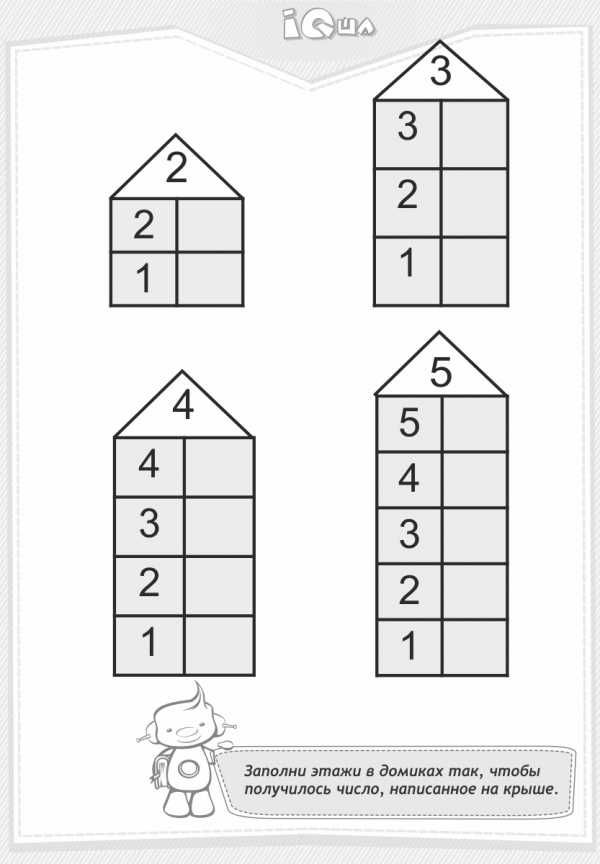
Засели домик цифрами

Состав числа в пределах 20

Для чтобы осваивать состав числа ребенку было интересно и увлекательно, можно воспользоваться проверенными методами и упражнениями.  Например, числовые карточки. На них изображено число и предметы, количество которых ему соответствует. Они наглядно иллюстрируют состав чисел, поэтому рекомендуем начать знакомство с темой с них.

Объяснять ребенку основы сложения можно помощью подручных предметов – пуговиц, камушков, конфет и т.д. Пригодятся здесь и числовые карточки: например, на одной из них изображено 1 яблоко, а на другой – 2 апельсина. Если сложить их вместе, то сколько фруктов получится? Ребенок посчитает все фрукты и назовет сумму, постепенно запоминая результаты сложения разных чисел.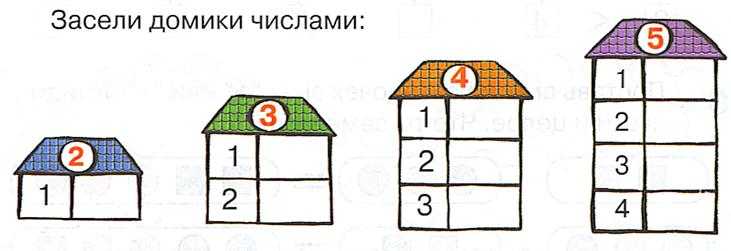

Когда ребенок начнет понимать, как складывать предметы, можно перейти к разбору состава числа. Родитель говорит, сколько предметов должно получиться в итоге, начиная с маленьких чисел,  а потом помогает ребенку собрать необходимое количество. Например, нужно собрать 4 банана. Берем карточку с изображением одного банана и спрашиваем, сколько еще нужно собрать. Затем добавляем карточку с двумя бананами и повторяем вопрос. Так вместе с ребенком вы переберете разные комбинации и освоите базовые составы числа.

Постепенно переходите к большим числам, где вариативность комбинаций увеличивается. Многократное проведение такого упражнения поможет закрепить в памяти состав числа и ребенок сможет легко его воспроизводить. Потом можно поупражняться таким же методом в вычитании. Взять несколько карточек например, 1 яблоко, 3 яблока и 4 яблока. Спросить у ребенка, сколько яблок на всех этих карточках. И спросить, какую карточку нужно убрать, чтобы получилось 7  яблок.

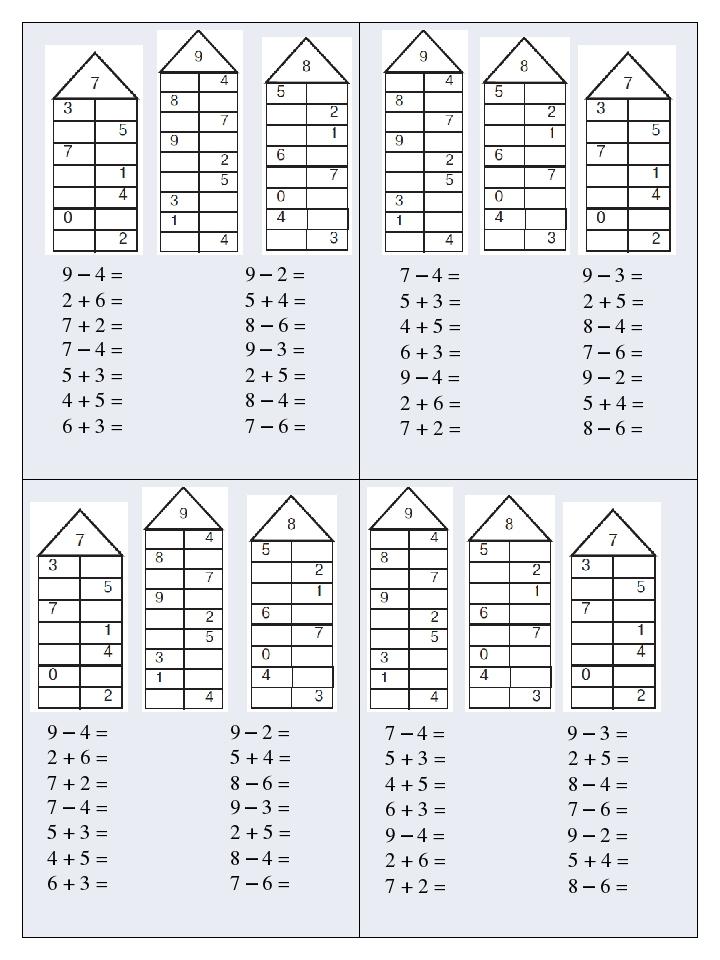
Для закрепления темы хорошо подойдут числовые домики – это следующий этап освоения состава чисел. Домик, где живут цифры, имеет несколько этажей с двумя окошками на каждом. На крыше находится число, которое разбивается на два числа-соседа на каждом этаже. Количество этажей зависит от количества возможных комбинаций, на которые можно разложить требуемое число.

Можно нарисовать такой домик самостоятельно. Например, для числа 4 будет 2 этажа: на одном числа-соседи – 2 и 2, на втором – 1 и 3. А можно воспользоваться готовыми числовыми домиками, где ребенку нужно будет только найти подходящие цифры соседи.

Начинать можно с первого или последнего этажа. Если у ребенка поначалу задание вызовет трудности, можно помочь ему, заполнив некоторые этажи. Позже можно объяснить секрет домика: переходя на этаж число становится на 1 больше или меньше.

После усвоения состава чисел до 10, можно переходить ко второму десятку, если ребенок уже его знает.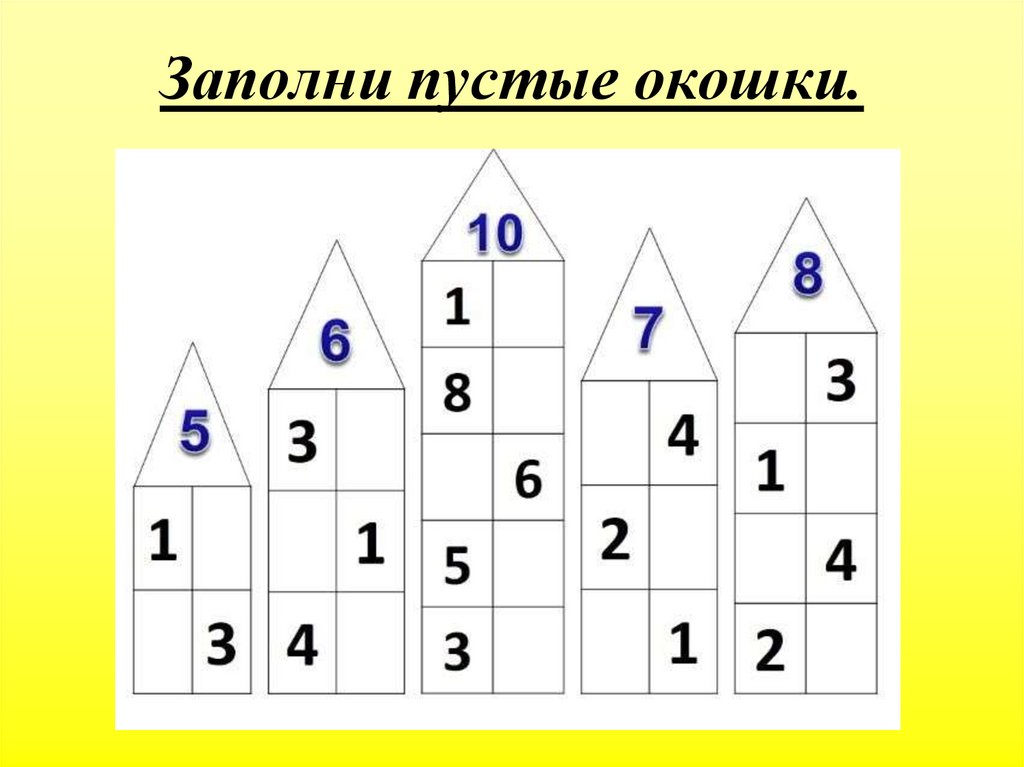 Тренажер состав чисел в пределах 20 поможет ему поупражняться.

При занятиях с ребенком важно помнить, что успех складывается из регулярности и поддержки. Хвалите его за успешные решения, это отлично мотивирует! Поддерживайте в трудных моментах и относитесь с пониманием к ошибкам. Так, небольшими шажочками и с вашей поддержкой, тема «Состав числа» будет успешно освоена ребенком.

Большая энциклопедия школьника

Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний, необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию, в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей, которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите

«Большую энциклопедию школьника» и найдите нужный ответ вместе с малышом!

Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены

Большая энциклопедия школьника — это твой надёжный путеводитель в мире знаний. Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной. С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей, ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли. Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик, ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!

Ребенок не хочет учить буквы Ребенок не хочет учить буквы — Понимаете, ведь надо что-то делать! — с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. — Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы …

Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный …

Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. № п/п Последовательность действий Выполнение действий 1. Записать общую формулу углеводорода. Общая формула углеводорода СхНу 2. Найти молярную массу углеводорода в общем виде. М(СхНу)=12х +у 3. Приравнять найденное в общем виде значение молярной массы к данному в …

У У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. — Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру …

математика — Какие номера домов?

спросил 3 года 4 месяца назад

Изменено 3 года, 4 месяца назад

Просмотрено 798 раз

$\begingroup$

После последнего вопроса «Какой номер углового дома?» здесь, возможно, более сложная версия.

Вставьте недостающие номера домов на карту, показанную ниже. Район населен любящими математику и языками (сумасшедшими) жителями, которые придумали интересные имена.

Есть 4 улицы: Рагаман, Санитар, Силач и Целый. Их имена имеют отношение (подсказки) к ответу. Поэтому, пожалуйста, объясните, как.

На каждой улице будет увеличиваться (или уменьшаться) количество домов. Каждый номера улиц имеют определенный шаблон и/или могут иметь уникальный свойство. Все они трехзначные числа.

Угловые дома, конечно же, удовлетворят требованиям по рисунку/свойствам как на пересечение улиц.

Примечание. Это может показаться неполной информацией, но это не так.

• математика
• знания
• узор

$\endgroup$

$\begingroup$

улица Рагаман

имеет номера домов в каждом блоке, которые представляют собой

анаграммы . В этом случае у нас есть 102, 120, 201, 210.

Целая улица

имеет номера домов, которые являются треугольными числами. В этом случае у нас есть 153, 171, 190, 210.

Стронгарм Стрит

имеет номера Армстронга. В этом случае у нас есть 153, 370, 371, 407.

Теперь улица Санитарная

идет 102, ?, 305, 407. Я полагаю, что это 1234 (целые положительные числа), соединенные с 02 03 05 07 (простые числа), поэтому окончательное число равно 203.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Свойства натуральных чисел — определения, примеры и часто задаваемые вопросы.

Свойства натуральных чисел относятся к результату четырех основных арифметических операций над натуральными числами. Натуральные числа — это набор целых чисел, кроме нуля. Эти числа используются в нашей повседневной деятельности и речи. Натуральные числа — это одна из классификаций действительных чисел, которая включает только положительные целые числа, т.е. 1, 2, 3, 4,5,6, ………. кроме нуля, дробей, десятичных и отрицательных чисел. Помните, что множество натуральных чисел не включает в себя отрицательные числа или нуль.

В этой статье вы подробно узнаете о свойствах натуральных чисел.

1.	Каковы свойства натуральных чисел?
2.	Свойство закрытия
3.	Ассоциативное свойство
4.	Коммутативная собственность
5.	Распределительная собственность
6.	Часто задаваемые вопросы о свойствах натуральных чисел

Каковы свойства натуральных чисел?

Натуральные числа — это числа, которые являются целыми положительными числами и включают числа от 1 до бесконечности (∞). Эти числа являются исчисляемыми и обычно используются для расчетов. Множество натуральных чисел в математике — это множество, начинающееся с 1, то есть {1,2,3,…}. Набор натуральных чисел обозначается символом N. Четыре свойства натуральных чисел таковы:

1. Свойство закрытия
2. Ассоциативное свойство
3. Коммутативное свойство
4. Распределительная собственность

Давайте рассмотрим их подробно.

Свойство закрытия

Свойство замыкания натуральных чисел гласит, что сложение и умножение двух или более натуральных чисел всегда дает натуральное число.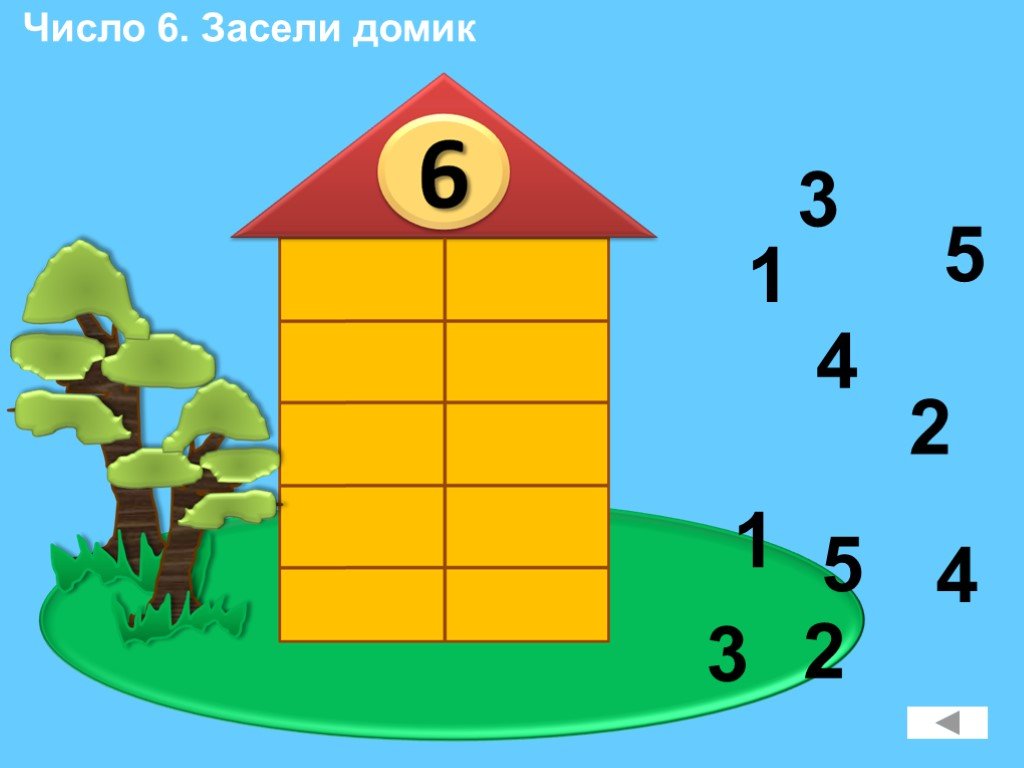 Проверим все четыре арифметические операции и все a, b ∈ N.

• Сложение: 1 + 5 = 6, 7 + 4 = 11 и т. д. Ясно, что полученное число или сумма является натуральным числом. Таким образом, a + b ∈ N для всех a, b ∈ N.
• Умножение: 2 × 5 = 10, 6 × 4 = 24 и т. д. Ясно, что полученное число или произведение — натуральное число. Таким образом, a × b ∈ N для всех a, b ∈ N.
• Вычитание: 8 – 5 = 3, 7 – 2 = -5 и т. д. Ясно, что результат может быть или не быть натуральным числом. Таким образом, a — b или b — a ∉ N для всех a, b ∈ N.
• Деление: 15 ÷ 5 = 3, 10 ÷ 3 = 3,33 и т. д. Ясно, что полученное число может быть или не быть натуральным числом. Таким образом, a ÷ b или b ÷ a ∉ N для всех a, b ∈ N.

Таким образом, мы можем заключить, что множество натуральных чисел всегда замкнуто относительно сложения и умножения, но не то же самое для вычитания и деления.

Ассоциативное свойство

Ассоциативное свойство натуральных чисел гласит, что сумма или произведение любых трех натуральных чисел остается неизменной, несмотря на изменение группировки чисел. Проверим все четыре арифметические операции и все a, b, c ∈ N.

• Дополнение: a + (b + c) = (a + b) + c. 3 + (15 + 1) = 19 и (3 + 15) + 1 = 19.
• Умножение: a × (b × c) = (a × b) × c. 3 × (15 × 1) = 45 и (3 × 15) × 1 = 45,
• Вычитание: а – (б – в) ≠ (а – б) – в. 2 – (15 – 1) = – 12 и (2 – 15) – 1 = – 14.
• Деление: a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c. 2 ÷ (3 ÷ 6) = 4 и (2 ÷ 3) ÷ 6 = 0,11.

Таким образом, мы можем заключить, что множество натуральных чисел ассоциативно при сложении и умножении, но не так при вычитании и делении. Итак, ассоциативность N формулируется следующим образом: для всех a, b, c ∈ N, a + (b + c) = (a + b) + c и a × (b × c) = (a × b ) × с

Коммутативное свойство

Коммутативное свойство натуральных чисел гласит, что сумма или произведение двух натуральных чисел остается неизменным даже после изменения порядка чисел. Проверим все четыре арифметических действия и все a, b ∈ N.

• Дополнение: a + b = b + a.
• Умножение: a × b = b × a
• Вычитание: а – б ≠ б – а
• Деление: а ÷ b ≠ b ÷ а

Следовательно, мы можем заключить, что множество натуральных чисел коммутативно при сложении и умножении, но не так при вычитании и делении. Итак, коммутативность N формулируется следующим образом: для всех a, b ∈ N, a + b = b + a и a × b = b × a

Операция	Свойство закрытия	Ассоциативное свойство	Коммутативное свойство
Дополнение	да	да	да
Вычитание	нет	нет	нет
Умножение	да	да	да
Подразделение	нет	нет	нет

Распределительная собственность

Распределительное свойство натуральных чисел утверждает, что любое выражение с тремя числами a, b и c, заданное в форме a (b + c), тогда оно разрешается как a × (b + c) = ab + ac или a (b — c) = ab — ca, что означает, что операнд a распределяется между двумя другими операндами, b и c.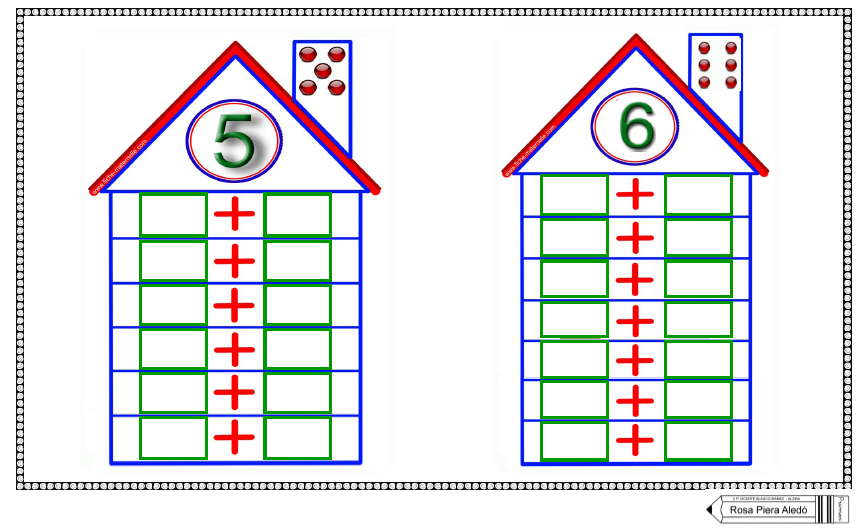

• Умножение натуральных чисел всегда дистрибутивнее сложения. а × (б + с) = аб + ас
• Умножение натуральных чисел также дистрибутивно по сравнению с вычитанием. а × (б – в) = аб – ас

Пример: 3 × (2 + 5) = 3 × 2 + 3 × 5

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

Пример: 3 × (2 − 5) = 3 × 2 − 3 × 5

3 × (2 −5) = 3×(−3) = −9

3 × 2 − 3 × 5 = 6 − 15 = −9

Статьи по теме

Ознакомьтесь с этими интересными статьями, посвященными свойствам натуральных чисел, для более глубокого понимания.

• Распределительное свойство умножения
• Коммутативное свойство
• Ассоциативное свойство
• Калькулятор свойств распределения

Часто задаваемые вопросы о свойствах натуральных чисел

Каковы свойства натуральных чисел в математике?

Свойства натуральных чисел:

1. Свойство замыкания
2. Ассоциативное свойство
3. Коммуникативное имущество
4. Распределительное имущество

Является ли множество натуральных чисел ассоциативным при делении?

Множество натуральных чисел НЕ является ассоциативным при делении.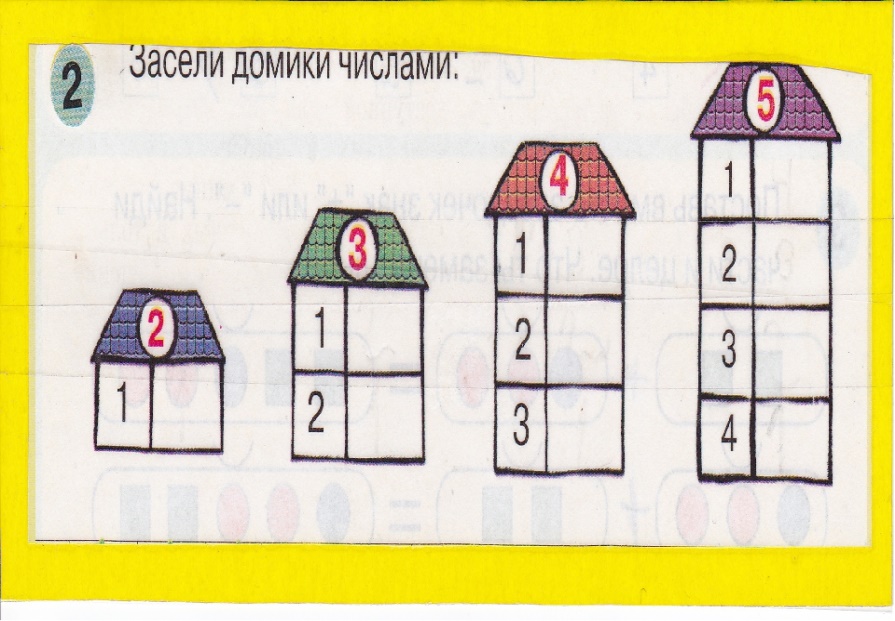 Например, рассмотрим три натуральных числа 6,4 и 2. Тогда: (6÷4)÷2 = 3÷2=1. 6÷(4÷2) = 6÷2 = 3. Таким образом, (6÷4)÷2 ≠ 6÷(4÷2).

Что вы подразумеваете под коммутативным свойством сложения?

Согласно коммутативному свойству сложения, натуральные числа можно складывать в любом порядке, и их ответ останется тем же. Формула для этого свойства такова: a + b = b + a, что верно для любых a, b ∈ N. Например, 1 + 2 или 2 + 1 дадут один и тот же ответ.

Что означает ассоциативное свойство сложения?

Ассоциативное свойство сложения — это свойство натуральных чисел, которое гласит, что сумма трех или более чисел не изменится даже при изменении группировки чисел. Соответствующее уравнение имеет вид a + ( b + c ) = ( a + b ) + c . Здесь группировка относится к тому, как данные числа расположены в скобках.

Какое уравнение показывает коммутативное свойство сложения?

Уравнение, показывающее коммутативность сложения, имеет вид «a + b = b + a». Возьмем пример: 4 + 3 = 3 + 4.