Знаки при умножении и делении: Умножение и деление отрицательных чисел

§ Умножение отрицательных чисел. Умножение рациональных чисел

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

• (−3) · (−6) = +18 = 18
• 2 · 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак «−».

Примеры умножения отрицательных и положительных чисел.

• (−0,3) · 0,5 = −0,15
• 1,2 · (−7) = −8,4

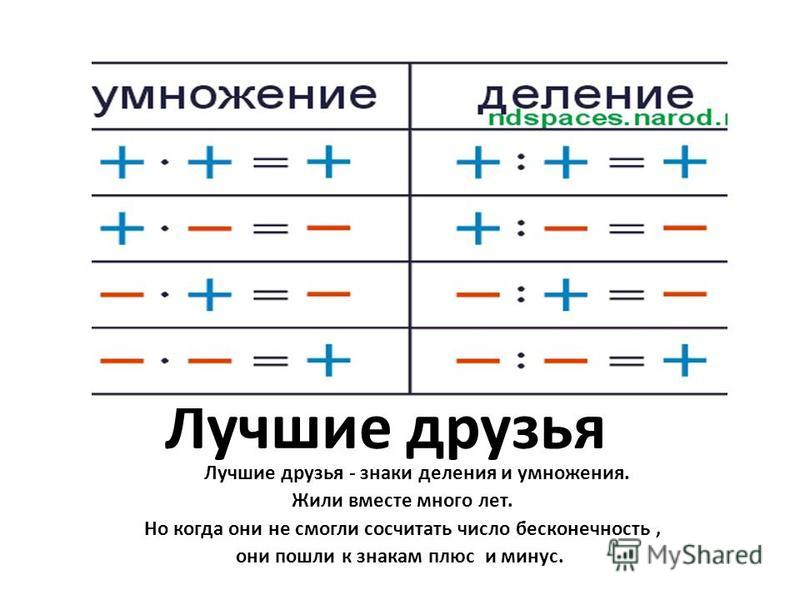
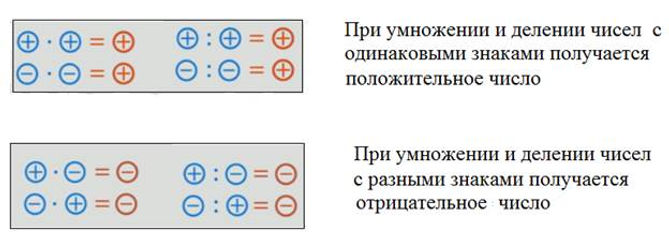
Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Запомните!

Минус на минус даёт плюс,

  Плюс на минус даёт минус.

+ · (+) = +	+ · (−) = −
− · (−) = +	− · (+) = −

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

Пример.

(−6) · (−3) · (−4) · (−2) · 12 · (−1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 · 3 · 4 · 2 · 12 · 1 = 1728

Конечный результат умножения исходных чисел будет:

(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

• 0 · a = 0
• a · 0 = 0
• a · 1 = a

Примеры:

• 0 · (−3) = 0
• 0,4 · 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица «−1».

Запомните!

При умножении на «−1» число меняется на противоположное.

В буквенном выражении это свойство можно записать:

a · (−1) = (−1) · a = −a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

Деление чисел с разными знаками: правило и примеры

В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.

Правило деления чисел с разными знаками

Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.

Правило деления чисел с разными знаками

При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.

В буквенном виде это выглядит так:

a÷-b=-a÷b

-a÷b=-a÷b.

Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.

Еще одна эквивалентная математическая формулировка данного правила имеет вид:

a÷b=a·b-1

Чтобы разделить числа a и b, имеющие разные знаки, нужно число a умножить на число, обратное числу b, то есть b-1. Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.

Рассмотрим теперь, как применять описанную выше теорию на практике.

Как делить числа с разными знаками? Примеры

Ниже мы рассмотрим несколько характерных примеров.

Пример 1. Как делить числа с разными знаками?

Разделим -35 на 7.

Сначала запишем модули делимого и делителя:

-35=35, 7=7.

Теперь разделим модули:

-357=357=5.

Допишем перед результатом знак минус и получим ответ:

-357=-5.

Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7. 

7-1=17. 

Теперь проведем умножение:

-35·17=—35·17=-357=-5.

Пример 2. Как делить числа с разными знаками?

Вычислим значение 8÷-60.

По правилу, имеем:

8÷-60=-8÷-60=-8÷60=-860.

Мы получили дробь, которую можно сократить на 4. После сокращения получаем:

8÷-60=-860=-215. 

Это и есть окончательный ответ. 

Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.

Пример 3. Как делить числа с разными знаками?

Разделим смешанное число -3322 на десятичную дробь 0,(23).

Модули делимого и делителя соответственно равны 3322 и 0,(23). Переводя 3322 в обыкновенную дробь, получаем:

3322=3·22+322=6922.

Делитель также представим в виде обыкновенной дроби:

0,(23)=0,23+0,0023+0,000023=0,231-0,01=0,230,99=2399.

Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:

-6922÷2399=-6922·9923=-32·91=-272=-1312.

В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д. 

В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается. При необходимости вычисляется его приближенное значение с необходимой точностью.

Пример 4. Как делить числа с разными знаками?

Разделим числа 57 и -23.

По правилу деления чисел с разными знаками, запишем равенство:

57÷-23=-57÷-23=-57÷23=-57·23.

Избавимся от иррациональности в знаменателе и получим окончательный ответ:

-57·23=-5·4314.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Как вставить символ умножения и знак деления в Word

Знак умножения × (также известный как знак умножения или знак размера ) является математическим знаком для операции умножения.

Есть несколько популярных представлений для операции умножения: крест ( × ), точка ( ⋅ ) или звездочка ( ∗ ).

См. также как поставить х в ворде.

Знак дивизии ÷ является математическим символом в форме Colon ( ∶ ), Obelus ( ÷ ), или Slash или Solidus ( /), или . обозначают оператор деления. В большинстве стандартов косая черта ( / ) используется в качестве знака деления для линейного представления или дробной черты для структурированного представления. Символы ÷ и ∶ могут определять диапазон данных.

Мы настоятельно рекомендуем использовать инструменты Equation для вставки любого типа уравнения или математических, финансовых или даже логических формул и выражений.

Строчная Латинская буква X часто заменяет знак умножения , но это ошибка, которую нужно избегать.

Чтобы создать идеальный документ, используйте один из следующих способов вставки умножения 9Символ 0004 или знак деления :

Стандартный способ : с помощью диалогового окна Символ:

Чтобы открыть диалоговое окно Символ , выполните следующие действия:

   1.    На вкладке Вставить в группе Символы нажмите кнопку Символ и нажмите Дополнительные символы… :

   2.   В диалоговом окне Symbol :

С помощью сочетания клавиш:

В Microsoft Word вы можете использовать Unicode для вставки любого из используемых символов:

	Горячая клавиша	Символ
Знак умножения	Введите 00d7 или 00D7 (неважно, прописные или строчные) и сразу нажмите Alt+X	×
Умножение Х	Введите 2715 и сразу нажмите Alt+X	✕
Вектор или перекрестное произведение символ	Введите 2a2f или 2A2F и сразу нажмите Alt+X	⨯
Средняя точка	Тип 00b7 или 00B7 и сразу нажмите Alt+X	·
Точка символ	Введите 22c5 или 22C5 и сразу нажмите Alt+X	⋅
Знак раздела	Введите 00f7 или 00F7 и сразу нажмите Alt+X	÷

Более быстрый способ : использование автозамены по математике:

Когда вы работаете с большим количеством документов и часто нужно вставить один специальный символ, вам не нужно вставлять уравнение каждый раз. Microsoft Word предлагает полезную функцию под названием AutoCorrect . Параметры AutoCorrect в Microsoft Word предлагают два разных способа быстрого добавления любого специального символа или даже большие куски текста:

• Использование в Заменить текст при вводе Функция Автозамены Опции.
• Использование параметров Math AutoCorrect :

Используя этот метод, вы можете использовать параметры Math AutoCorrect без вставки уравнения. Чтобы включить или выключить AutoCorrect символов Math , выполните следующие действия:

   1.   На вкладке Файл нажмите Параметры :

   2.   В диалоговом окне Параметры Word на Вкладка Правописание нажмите кнопку Параметры автозамены… :

   3.   В диалоговом окне AutoCorrect на вкладке Math AutoCorrect выберите параметр Использовать правила Math AutoCorrect за пределами математических областей :

После нажатия OK вы можете использовать любое из перечисленных Имен символов , и Microsoft Word заменит их соответствующими символами:

Примечание : Если вам не нужна последняя замена, нажмите Ctrl+Z , чтобы отменить ее.

Основные математические символы | Словарь

математика (BrE) | математика (AmE) — это сокращенная форма математика

На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.

+
знак плюс/дополнение

Знак плюс означает:

а. понятие

положительное

Любое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.

Таким образом, +5 (плюс пять) и 5 ​​(пять) — одно и то же число.

б. операция сложения

3 + 5 = 8
три плюс пять равно восьми
пять прибавить к трем, получится восемь
три прибавить к пяти, получится восемь

Сложение дает нам сумма . В 3 + 5 = 8 сумма равна восьми.

—

знак минус/знак вычитания

Знак минус означает:

а.

понятие отрицательного

Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.

-3
минус три

б. операция вычитания

8 — 5 = 3
восемь минус пять равно трем
пять вычесть из восьми равно трем
если из восьми вычесть пять, то получится три
если из восьми вычесть пять, то получится три

Вычитание дает нам разность . В 8 — 5 = 3 разница три.

×

знак умножения / знак умножения

Знак раз представляет:

умножение

5 x 6 = 30
пять умножить на шесть равно тридцати
пять умножить на шесть равно тридцати
пять шестерок равно тридцати
если умножить 5 на 6 получится тридцать

Умножение дает нам продукт . В 5 х 6 = 30 произведение равно 30.

÷ ИЛИ /

знак деления

Знак деления означает:

отделение

15 ÷ 3 = 5
15 / 3 = 5
пятнадцать разделить на три равно пяти
пять получится пятнадцать трижды
если пятнадцать разделить на три получится пять
если три разделить на пятнадцать получится пять

Деление дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.

Подытожим вышеописанные четыре операции следующим образом:

операция			результат
дополнение	«плюс»	2 + 2 = 4	сумма
вычитание	«минус»	5 — 3 = 2	разница
умножение	«раз»	3 х 5 = 15	товар
отдел	«делится на»	21/7 = 3	частное

=

знак равенства

Знак равенства представляет равенство :

3 + 4 = 7
три плюс четыре равно семь

Обратите внимание, что мы обычно говорим, что равно , НЕ равно:

• два плюс два равно четыре
• два плюс два равно четырем

<
меньше

3 < 4
три меньше четырех

>

больше

4 > 3
четыре больше трех

≠

НЕ равно

x ≠ z
x не равно z

≥

больше или равно

x ≥ z
x больше или равно z

≤

меньше или равно

z ≤ x
z меньше или равно x

¾

дробь

см.