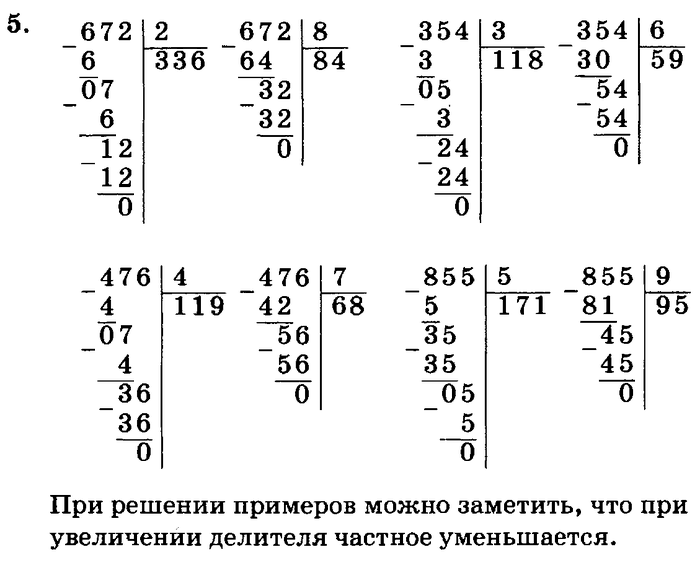
Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
- Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок.
Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум.
То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.
Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Деление столбиком. Онлайн калькулятор | Математика
- Как записывать деление в столбик
- Как делить столбиком
- Деление столбиком с остатком
- Калькулятор деления столбиком
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком.
Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль.
Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0.
Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184.
Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить
.
Как выполнить длинное деление с двумя цифрами + пример
В сегодняшней статье мы собираемся объяснить
как решать двузначное деление. Перед тем, как начать учиться решать двузначное деление, важно, чтобы вы ознакомились с этими терминами, потому что мы будем использовать их позже.
Дивиденд: число, которое делится.
Частное: результат деления.
Остаток: сумма, оставшаяся после деления.
Увидев это, вы знаете, где разместить каждое число в дивизионе. Теперь нам нужно выполнить следующие шаги:
- Возьмите первые цифры делимого, столько же цифр, сколько и у делителя. Если число, взятое из делимого, меньше делителя, нужно взять следующую цифру делимого.
- Разделите первое число делимого (или два первых числа, если на предыдущем шаге была другая цифра) на первую цифру делителя. Запишите результат этого деления в пространстве частного.
- Умножьте цифру частного на делитель, запишите результат под делимым и вычтите его. Если вы не можете, потому что делимое меньше, вам придется выбирать меньшее число в частном, пока оно не сможет вычитаться.
- После вычитания отбросить следующую цифру делимого и повторять с шага 2 до тех пор, пока в делимом не останется оставшихся чисел.
Это концепция, но мы рассмотрим ее на примере.
Мы собираемся решить следующее двузначное деление:
- Возьмем первые цифры делимого: в данном случае 57. Но так как 57 меньше 73, вы должны взять еще одну цифру: 573.
- Чтобы разделить 573 на 73, берем первые две цифры делимого: 57 и делим их на первую цифру делителя:
57 ÷ 7 = 8
- Запишите 8 в частном и умножьте на делитель:
8 x 73 = 584
Но 584 больше 573; следовательно, 8 «не подходит». Вы должны выбрать предыдущее число и снова умножить:
7 x 73 = 511
511 меньше, чем делимое; поэтому 7 «подходит». Мы пишем 511 под цифрами делимого, а затем делим и вычитаем:
- Отбросьте следующую цифру делимого, то есть 8. Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:
Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:Разделите первые две цифры делимого на первую цифру делителя и запишите это число в пространстве частного:
62 ÷ 7 = 8
Умножьте эту цифру на делитель:
8 x 73 = 584
584 меньше 628; следовательно, мы можем вычесть:
628 – 584 = 44
Результат этого деления 78 и остаток 44.
Я надеюсь, что из этого поста вы узнали, как выполнять двузначное деление.
Не стесняйтесь оставлять свои комментарии!
А если вы хотите узнать больше о математике, войдите в систему Smartick
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Последние сообщения от Smartick (посмотреть все)
Деление многозначных десятичных знаков — Common Core: Математика для 6-го класса
All Common Core: Математические ресурсы для 6-го класса
6 Диагностические тесты 186 практических тестов Вопрос дня Карточки Learn by Concept
Common Core: Справка по математике для 6-го класса »
Система счисления »
Свободное сложение, вычитание, умножение и деление многозначных десятичных чисел: CCSS.
Math.Content.6.NS.B.3 »
Деление многозначных десятичных дробей
Решите:
Возможные ответы:
Правильный ответ:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на одну позицию в делителе, мы также должны переместить десятичную запятую на одну позицию в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 76 может войти в 197
76 может войти в 197 два раза, поэтому мы пишем 2 над 7 в делимом:Затем мы умножаем 2 на 76 и записываем это произведение под 197 и вычитаем:
Теперь мы уменьшаем 6 из делимого, чтобы получить 45 в 456.
Подумайте: сколько раз можно 76 перейти в 456?
76 может войти в число 465 шесть раз, поэтому мы пишем 6 над 6 в делимом:
Затем мы умножаем 6 на 76 и записываем это произведение под 456 и вычитаем:
У нас остается без остатка и конечное частное 2,6
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 12 может войти в 8
12 не может войти в 8, поэтому мы пишем 0 над 8 в делимом:
Поскольку 12 не может входим в число 8, объединяем разряд единиц и разряд десятых и думаем, сколько раз 12 может войти в число 85. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 85.
Подумайте: сколько раз может 12 войти в 85
12 может войти в 85 семь раз, поэтому мы пишем 7 над 5 в делимом:
Затем мы умножаем 12 на 7 и записываем это произведение под 85 и вычитаем:
Теперь мы уменьшаем 8 из делимого, чтобы превратить 1 в 18.
Подумайте: сколько раз можно 12 перейти в 18?
12 может войти в 18 один раз, поэтому мы пишем 1 над 8 в делимом:
Затем мы умножаем 12 на 1 и записываем это произведение под 18 и вычитаем:
Теперь у нас осталось с 6 в нашем делимом, и мы не можем умножить 12 на что-либо, чтобы получить 6. Мы присоединяем или добавляем ноль к нашему делимому, который мы можем отнести к 6, и теперь это будет 60. Мы не изменили значение нашего делимое, мы добавили ноль, чтобы число делилось на 12.
Подумайте: сколько раз 12 может перейти в 60?
12 может войти в 60 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 12 и 5 и записываем это произведение под 60 и вычитаем:
У нас остается без остатка и окончательное частное 0,715
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 9 может войти в 8
9 не может войти в 8, поэтому мы пишем 0 над 8 в делимом:
Так как 9 не может идем в 8, мы объединяем разряд единиц и разряд десятых и думаем, сколько раз 9 может войти в 87. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 87.
Подумайте: сколько число 9 может входить в число 87
9 может входить в число 87 девять раз, поэтому мы пишем 9над 7 в делимом:
Затем мы умножаем 9 на 9 и записываем это произведение под 87 и вычитаем:
Теперь мы уменьшаем 3 из делимого, чтобы превратить 6 в 63.
Подумайте: сколько раз 9 может быть 63?
9 может войти в 63 семь раз, поэтому мы пишем 7 над 3 в делимом:
Затем мы умножаем 9 на 7 и записываем это произведение под 63 и вычитаем:
У нас не осталось остатка и окончательное частное 0,97
Сообщить об ошибке
Правильный ответ: 74
7
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на один разряд в делителе, мы также должны переместить десятичный разряд на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 18 может войти в 45
18 может войти в 45 два раза, поэтому мы пишем 2 вместо 5 в делимом:
Затем мы умножаем 2 на 18 и записываем это произведение под 45 и вычитаем:
Теперь 18 нельзя умножить на целое число, чтобы получить 9, поэтому приложите или добавьте ноль к делимому, чтобы получить число, которое делится на 18. Мы не меняем значение делимого, добавляя ноль. Перенесите этот 0 рядом с 9, чтобы получить 90.
Подумайте: сколько раз 18 может превратиться в 90?
18 может войти в 90 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 5 и 18 и записываем это произведение под 90 и вычитаем:
У нас не остается остатка и окончательное частное равно 2,5
Сообщить об ошибке
Решить:
7
7 Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 52 может войти в 1
52 не может войти в 1, поэтому мы пишем 0 над 1 в делимом:
Мы не использовали 1 в разряде сотен, поэтому теперь мы подставляем 0 в разряд десятков и пытаемся разделить его на 52
Подумайте: сколько раз 52 может входить в 10
52 не может входить в 10, поэтому мы пишем 0 над 0 в делимом:
Мы не использовали 10, поэтому теперь мы подставляем 1 из разряда единиц и пытаемся разделить его на 52
Подумайте: сколько раз 52 может войти в 101
52 может войти в 101 один раз, поэтому мы пишем 1 над 1 в делимом:
Затем мы умножаем 52 на 1 и записываем это произведение под 101 и вычтите:
Теперь мы уменьшим 4 из делимого, чтобы превратить 49 в 494. напишите 9 над 4 в делимом:
Затем мы умножаем 52 на 9 и пишем это произведение под 494 и вычитаем:
Теперь 52 нельзя умножить на целое число, чтобы получить 26, поэтому приложение или добавьте ноль к делимому, чтобы получить число делится на 52. Мы не меняем значение делимого, добавляя ноль. Сократите этот 0 рядом с 26, чтобы получить 260.
Подумайте: сколько раз 52 может перейти в 260?
52 может войти в 260 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 52 на 5 и записываем это произведение под 260 и вычитаем:
У нас не остается остатка, и окончательное частное равно 1,95
Сообщить об ошибке
7Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь непосредственно над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 2 может войти в 4
2 может войти в 4 два раза, поэтому мы пишем 2 над 4 в делимом:
Далее, мы умножаем 2 на 2 и пишем это произведение под 4 и вычитаем:
Теперь мы уменьшаем 0 из делимого, чтобы превратить 0 в 00.
Подумайте: сколько раз 2 может войти в 0
2 может перейти в 0 ноль раз, поэтому мы пишем 0 вместо 0 в делимом:
Затем мы умножаем 2 на 0 и пишем это произведение под 0 и вычитаем:
Теперь мы уменьшаем 9 из делимого, чтобы сделать 0 в 9.
2 может превратиться в 9 четыре раза, поэтому мы пишем 4 вместо 9 в делимом:
Затем мы умножаем 2 и 4 и пишем это произведение под 9 и вычитаем:
Теперь 2 нельзя умножить на целое число, чтобы получить a 1, поэтому добавьте ноль к делимому, чтобы получить число, делящееся на 2. Мы не меняем значение делимого, добавляя ноль. Поместите этот 0 рядом с 1, чтобы получить 10.
Подумайте: сколько раз 2 может быть 10?
2 может войти в 10 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 2 и 5 и записываем это произведение под 10 и вычитаем:
У нас остается без остатка и конечное частное 204,5
Сообщить об ошибке
Какое число в задаче является делимым?
Возможные ответы:
Ни один из вариантов ответа не является правильным.
Правильный ответ:
Объяснение:
Делимое — это то, что вы делите или делите в задаче на деление. Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Сообщить об ошибке
Какая модель правильно представляет блок сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,24. Итак, заштрихуйте 24 квадратика, в десятичной модели.
Существует множество прямоугольников площадью 0,24. Вам нужно заштриховать тот, который имеет длину 0,6.
Отсутствует коэффициент 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,6 равна 0,24. Следовательно, 0,24 ÷ 0,6 = 0,4
Сообщить об ошибке
Решите задачу, используя предоставленную модель области.
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,12. Итак, заштрихуйте 12 маленьких квадратов в десятичной модели.
Существует множество прямоугольников площадью 0,12. Вам нужно заштриховать тот, который имеет длину 0,3.
Отсутствующий коэффициент равен 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,3 равна 0,12. Следовательно, 0,12 ÷ 0,3 = 0,4
Сообщить об ошибке
Какая модель правильно представляет блок сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.