правила, примеры, решения, решение дробей
Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Определение 1Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Пример 1Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Пример 2Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Определение 2Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Пример 3Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
В данном примере нам этого не нужно делать.
Найдите разность 199 — 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 11112.
Краткая запись всего решения — 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Пример 5Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Тогда предыдущий пример можно решить иначе.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Пример 6Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Определение 3Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Пример 8Вычислите разность 644 — 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Пример 9Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог — 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.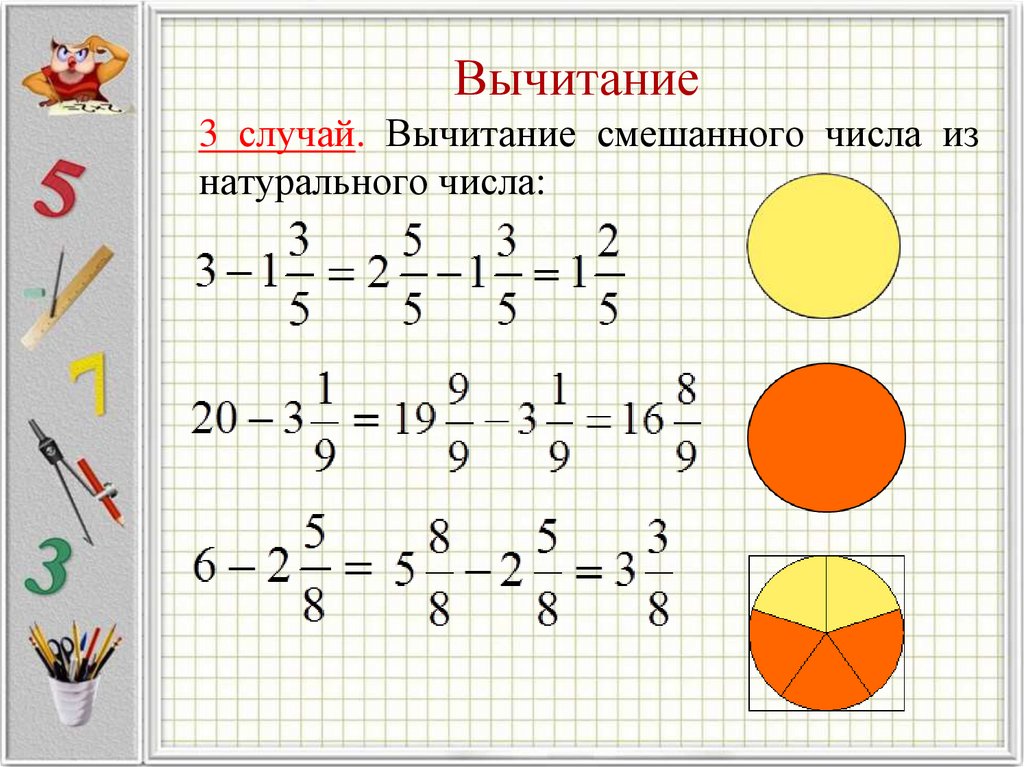
Сложение и вычитание дробей
Сложение и вычитание дробейНавигация по странице:
- Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение обыкновенных дробей
- Сложение смешаных чисел
- Вычитание дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание обыкновенных дробей
- Вычитание смешаных чисел
Сложение дробей
Сложение дробей с одинаковыми знаменателями.

Определение.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | b | = | a + b |
| c | c | c |
Примеры сложения дробей с одинаковыми знаменателями
Пример 1.
Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2.
Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.

Примеры сложения обыкновенных дробей
Пример 3.
Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | 3 | = | 3 | = | 1 | |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4.
Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чисел
Примеры сложения смешанных чисел
Пример 5.
Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6.
Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробей
Вычитание дробей с одинаковыми знаменателями.

Определение.
Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | — | b | = | a — b |
| c | c | c |
Примеры вычитания дробей с одинаковыми знаменателями
Пример 7.
Найти разность двух дробей с одинаковыми знаменателями:
| 3 | — | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8.
Найти разность двух дробей с одинаковыми знаменателями:
| 8 | — | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.

Примеры вычитания обыкновенных дробей
Пример 9.
Найти разность двух дробей:
| 5 | — | 1 | = | 5 | — | 1·3 | = | 5 | — | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10.
Найти разность двух дробей:
| 3 | — | 1 | = | 3·3 | — | 1·5 | = | 9 | — | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.

Примеры вычитания смешанных чисел
Пример 11.
Найти разность двух смешанных чисел:
| 2 | 1 | — | 1 | 1 | = | 2 | 1·3 | — | 1 | 1·2 | = | (2 — 1) | + | 3 | — | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12.
Найти разность двух смешанных чисел:
| 3 | 1 | — | 1 | 3 | = | 3 | 1·4 | — | 1 | 3·3 | = | 3 | 4 | — | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | — | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13.
Найти разность двух смешанных чисел:
| 1 | 1 | — | 3 | 2 | = | 1 | 1 | — | 3 | 2·2 | = | 1 | 1 | — | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | — | 3 | = | -2 | — | 3 | = | -2 | — | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь
Онлайн калькуляторы дробей
Онлайн упражнения с дробями
Как складывать неправильные дроби с разными знаменателями.
 Как научиться вычитать дроби с разными знаменателями
Как научиться вычитать дроби с разными знаменателямиОбратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили.
 В результате мы почти найдем ответ;
В результате мы почти найдем ответ; - Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия.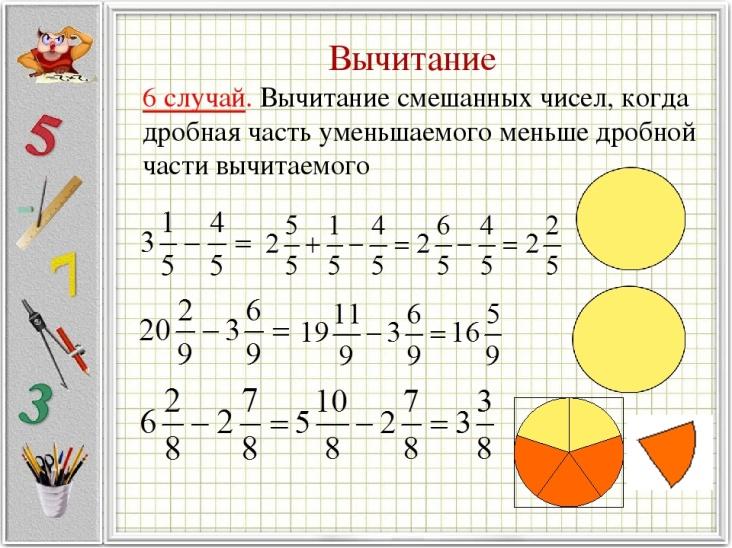 Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти , а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)
В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)
Сложение смешанных чисел или смешанных дробей.
Сложение происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби.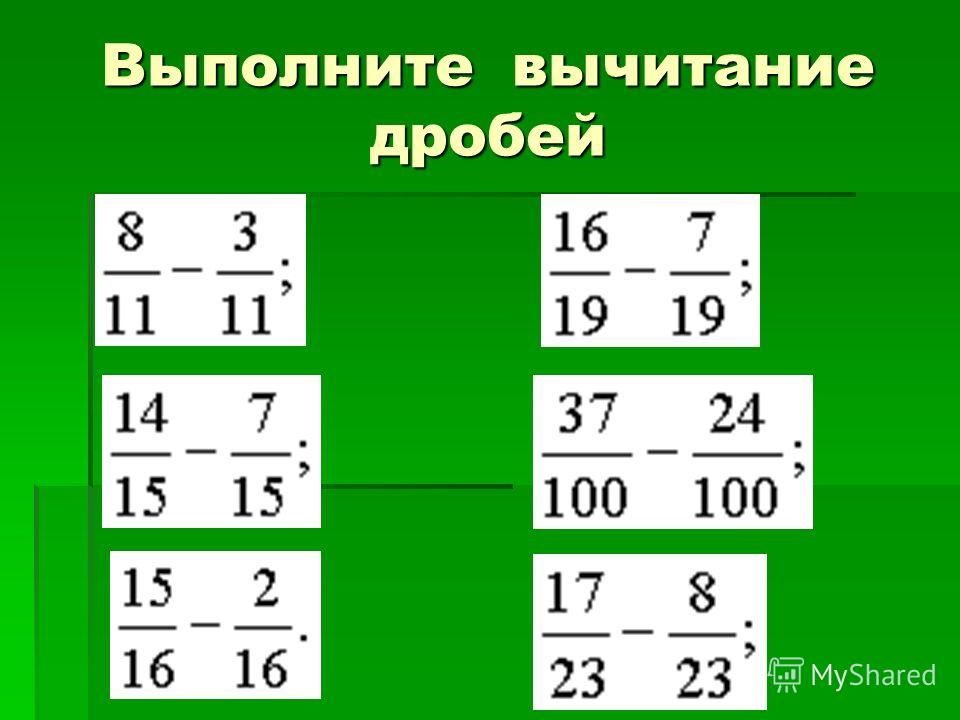 В зависимости от типа выражения переходим к алгоритму решения.
В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)
Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)
Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)
Ответ: весь торт съели.
Рассмотрим дробь $\frac63$. Ее величина равна 2, так как $\frac63 =6:3 = 2$. А что произойдет, если числитель и знаменатель умножить на 2? $\frac63 \times 2=\frac{12}{6}$. Очевидно, величина дроби не изменилась, так $\frac{12}{6}$ как у также равно 2. Можно умножить числитель и знаменатель на 3 и получить $\frac{18}{9}$, или на 27 и получить $\frac{162}{81}$ или на 101 и получить $\frac{606}{303}$. В каждом из этих случаев величина дроби, которую мы получаем, разделив числитель на знаменатель, равна 2. Это означает, что не изменилась.
Такая же закономерность наблюдается и в случае других дробей. Если числитель и знаменатель дроби $\frac{120}{60}$ (равной 2) разделить на 2 (результат $\frac{60}{30}$), или на 3 (результат $\frac{40}{20}$), или на 4 (результат $\frac{30}{15}$) и так далее, то в каждом случае величина дроби остается неизменной и равной 2.
Это правило распространяется также на дроби, которые не равны целому числу .
Если числитель и знаменатель дроби $\frac{1}{3}$ умножить на 2, мы получим $\frac{2}{6}$, то есть величина дроби не изменилась. И в самом деле, если вы разделите пирог на 3 части и возьмете одну из них или разделите его на 6 частей и возьмете 2 части, вы в обоих случаях получите одинаковое количество пирога. Следовательно, числа $\frac{1}{3}$ и $\frac{2}{6}$ идентичны. Сформулируем общее правило.
Числитель и знаменатель любой дроби можно умножить или разделить на одно и то же число, и при этом величина дроби не изменяется.
Это правило оказывается очень полезным. Например, оно позволяет в ряде случаев, но не всегда, избежать операций с большими числами.
Например, мы можем разделить числитель и знаменатель дроби $\frac{126}{189}$ на 63 и получить дробь $\frac{2}{3}$ с которой гораздо проще производить расчеты. Еще один пример. Числитель и знаменатель дроби $\frac{155}{31}$ можем разделить на 31 и получить дробь $\frac{5}{1}$ или 5, поскольку 5:1=5.
В этом примере мы впервые встретились с дробью, знаменатель которой равен 1 . Такие дроби играют важную роль при вычислениях. Следует помнить, что любое число можно разделить на 1 и при этом его величина не изменится. То есть $\frac{273}{1}$ равно 273; $\frac{509993}{1}$ равно 509993 и так далее. Следовательно, мы можем не разделять числа на , поскольку каждое целое число можно представить в виде дроби со знаменателем 1.
С такими дробями, знаменатель которых равен 1, можно производить те же арифметические действия, что и со всеми остальными дробями: $\frac{15}{1}+\frac{15}{1}=\frac{30}{1}$, $\frac{4}{1} \times \frac{3}{1}=\frac{12}{1}$.
Вы можете спросить, какой прок от того, что мы представим целое число в виде дроби, у которой под чертой будет стоять единица, ведь с целым числом работать удобнее. Но дело в том, что представление целого числа в виде дроби дает нам возможность эффективнее производить различные действия, когда мы имеем дело одновременно и с целыми, и с дробными числами. Например, чтобы научится складывать дроби с разными знаменателями . Предположим, нам надо сложить $\frac{1}{3}$ и $\frac{1}{5}$.
Например, чтобы научится складывать дроби с разными знаменателями . Предположим, нам надо сложить $\frac{1}{3}$ и $\frac{1}{5}$.
Мы знаем, что складывать можно только те дроби, знаменатели которых равны. Значит, нам нужно научиться приводить дроби к такому виду, когда их знаменатели равны. В этом случае нам опять пригодится то, что можно умножать числитель и знаменатель дроби на одно и то же число без изменения ее величины.
Сначала умножим числитель и знаменатель дроби $\frac{1}{3}$ на 5. Получим $\frac{5}{15}$, величина дроби не изменилась. Затем умножим числитель и знаменатель дроби $\frac{1}{5}$ на 3. Получим $\frac{3}{15}$, опять величина дроби не изменилась. Следовательно, $\frac{1}{3}+\frac{1}{5}=\frac{5}{15}+\frac{3}{15}=\frac{8}{15}$.
Теперь попробуем применить эту систему к сложению чисел, содержащих как целую, так и дробную части.
Нам надо сложить $3 + \frac{1}{3}+1\frac{1}{4}$. Сначала переведем все слагаемые в форму дробей и получим: $\frac31 + \frac{1}{3}+\frac{5}{4}$. Теперь нам надо привести все дроби к общему знаменателю, для этого мы числитель и знаменатель первой дроби умножаем на 12, второй — на 4, а третьей — на 3. В результате получаем $\frac{36}{12} + \frac{4}{12}+\frac{15}{12}$, что равно $\frac{55}{12}$. Если вы хотите избавиться от неправильной дроби , ее можно превратить в число, состоящее из целой и дробной частей: $\frac{55}{12} = \frac{48}{12}+\frac{7}{12}$ или $4\frac{7}{12}$.
Теперь нам надо привести все дроби к общему знаменателю, для этого мы числитель и знаменатель первой дроби умножаем на 12, второй — на 4, а третьей — на 3. В результате получаем $\frac{36}{12} + \frac{4}{12}+\frac{15}{12}$, что равно $\frac{55}{12}$. Если вы хотите избавиться от неправильной дроби , ее можно превратить в число, состоящее из целой и дробной частей: $\frac{55}{12} = \frac{48}{12}+\frac{7}{12}$ или $4\frac{7}{12}$.
Все правила, позволяющие проводить операции с дробями , которые мы с вами только что изучили, также справедливы и в случае отрицательных чисел. Так, -1: 3 можно записать как $\frac{-1}{3}$, а 1: (-3) как $\frac{1}{-3}$.
Поскольку как при делении отрицательного числа на положительное, так и при делении положительного числа на отрицательное в результате мы получаем отрицательные числа, в обоих случаях мы получим ответ в виде отрицательного числа. То есть
$(-1) : 3 = \frac{1}{3}$ или $1: (-3) = \frac{1}{-3}$. Знак минус при таком написании относится ко всей дроби целиком, а не отдельно к числителю или знаменателю.
С другой стороны, (-1) : (-3) можно записать как $\frac{-1}{-3}$, а поскольку при делении отрицательного числа на отрицательное число мы получаем положительное число, то $\frac{-1}{-3}$ можно записать как $+\frac{1}{3}$.
Сложение и вычитание отрицательных дробей проводят по той же схеме, что и сложение, и вычитание положительных дробей. Например, что такое $1- 1\frac13$? Представим оба числа в виде дробей и получим $\frac{1}{1}-\frac{4}{3}$. Приведем дроби к общему знаменателю и получим $\frac{1 \times 3}{1 \times 3}-\frac{4}{3}$, то есть $\frac{3}{3}-\frac{4}{3}$, или $-\frac{1}{3}$.
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
Правила сложения обыкновенных. Сложение дробей с целыми числами и разными знаменателями
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные.
 Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше; - Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Числителем, а то, на которое делят — знаменателем.
Чтобы записать дробь, напишите сначала ее числитель, затем проведите под этим числом горизонтальную черту, а под чертой напишите знаменатель. Горизонтальная , разделяющая числитель и знаменатель, называется дробной чертой. Иногда ее изображают в виде наклонной «/» или «∕». При этом, числитель записывается слева от черты, а знаменатель справа. Так, например, дробь «две третьих» запишется как 2/3. Для наглядности числитель обычно пишут в верхней части строки, а знаменатель — в нижней, то есть вместо 2/3 можно встретить: ⅔.
Чтобы рассчитать произведение дробей, умножьте сначала числитель одной дроби на числитель другой. Запишите результат в числитель новой дроби . После этого перемножьте и знаменатели. Итоговое значение укажите в новой дроби . Например, 1/3 ? 1/5 = 1/15 (1 ? 1 = 1; 3 ? 5 = 15).
Запишите результат в числитель новой дроби . После этого перемножьте и знаменатели. Итоговое значение укажите в новой дроби . Например, 1/3 ? 1/5 = 1/15 (1 ? 1 = 1; 3 ? 5 = 15).
Чтобы поделить одну дробь на другую, умножьте сначала числитель первой на знаменатель второй. То же произведите и со второй дробью (делителем). Или перед выполнением всех действий сначала «переверните» делитель, если вам так удобнее: на месте числителя должен оказаться знаменатель. После этого умножьте знаменатель делимого на новый знаменатель делителя и перемножьте числители. Например, 1/3: 1/5 = 5/3 = 1 2/3 (1 ? 5 = 5; 3 ? 1 = 3).
Источники:
- Основные задачи на дроби
Дробные числа позволяют выражать в разном виде точное значение величины. С дробями можно выполнять те же математические операции, что и с целыми числами: вычитание, сложение, умножение и деление. Чтобы научиться решать дроби , надо помнить о некоторых их особенностях. Они зависят от вида дроби , наличия целой части, общего знаменателя. Некоторые арифметические действия после выполнения требуют сокращения дробной части результата.
Некоторые арифметические действия после выполнения требуют сокращения дробной части результата.
Вам понадобится
- — калькулятор
Инструкция
Внимательно посмотрите на числа. Если среди дробей есть десятичные и непрвильные, иногда удобнее вначале выполнить действия с десятичными, а затем перевести их в неправильный вид. Можете перевести дроби в такой вид изначально, записав значение после запятой в числитель и поставив 10 в знаменатель. При необходимости сократите дробь, разделив числа выше и ниже на один делитель. Дроби, в которых выделяется целая часть, приведите к неправильному виду, умножив её на знаменатель и прибавив к результату числитель. Данное значения станет новым числителем дроби . Чтобы выделить целую часть из первоначально неправильной дроби , надо поделить числитель на знаменатель. Целый результат записать от дроби . А остаток от деления станет новым числителем, знаменатель дроби при этом не меняется. Для дробей с целой частью возможно выполнение действий отдельно сначала для целой, а затем для дробной частей. Например, сумма 1 2/3 и 2 ¾ может быть вычислена :
Для дробей с целой частью возможно выполнение действий отдельно сначала для целой, а затем для дробной частей. Например, сумма 1 2/3 и 2 ¾ может быть вычислена :
— Переведение дробей в неправильный вид:
— 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
— Суммирование отдельно целых и дробных частей слагаемых:
— 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾) = 3 +(8/12 + 9/12) = 3 + 17/12 = 3 + 1 5/12 = 4 5/12.
Перепишите их через разделитель «:» и продолжите обычное деление.
Для получения конечного результата полученную дробь сократите, разделив числитель и знаменатель на одно целое число, наибольшее возможное в данном случае. При этом выше и ниже черты должны быть целые числа.
Обратите внимание
Не выполняйте арифметические действия с дробями, знаменатели которых отличаются. Подберите такое число, чтобы при умножении на него числителя и знаменателя каждой дроби в результате знаменатели обеих дробей были равны.
Полезный совет
При записи дробных чисел делимое пишется над чертой.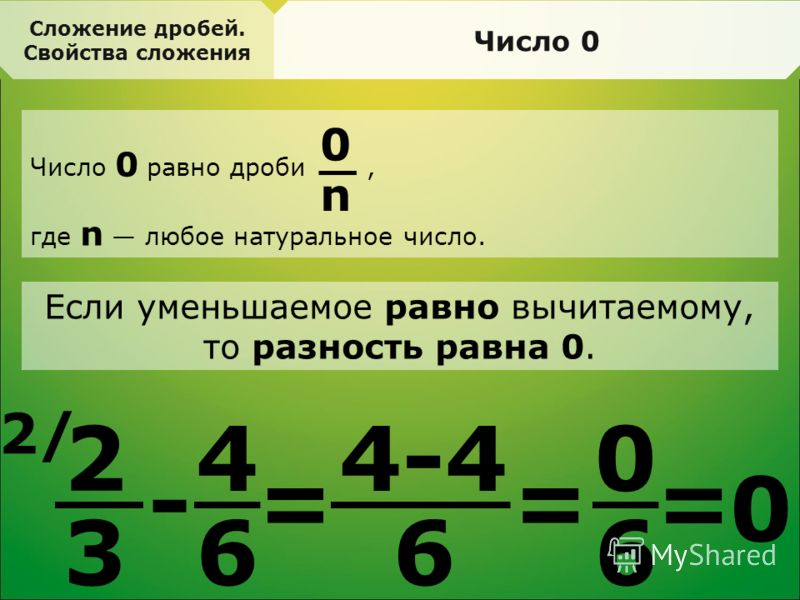 Эта величина обозначается как числитель дроби. Под чертой записывается делитель, или знаменатель, дроби. Например, полтора килограмма риса в виде дроби запишется следующим образом: 1 ½ кг риса. Если знаменатель дроби равен 10, такую дробь называют десятичной. При этом числитель (делимое) пишется справа от целой части через запятую: 1,5 кг риса. Для удобства вычислений такую дробь всегда можно записать в неправильном виде: 1 2/10 кг картофеля. Для упрощения можно сократить значения числителя и знаменателя, поделив их на одно целое число. В данном примере возможно деление на 2. В результате получится 1 1/5 кг картофеля. Удостоверьтесь, что числа, с которыми вы собираетесь выполнять арифметические действия, представлены в одном виде.
Эта величина обозначается как числитель дроби. Под чертой записывается делитель, или знаменатель, дроби. Например, полтора килограмма риса в виде дроби запишется следующим образом: 1 ½ кг риса. Если знаменатель дроби равен 10, такую дробь называют десятичной. При этом числитель (делимое) пишется справа от целой части через запятую: 1,5 кг риса. Для удобства вычислений такую дробь всегда можно записать в неправильном виде: 1 2/10 кг картофеля. Для упрощения можно сократить значения числителя и знаменателя, поделив их на одно целое число. В данном примере возможно деление на 2. В результате получится 1 1/5 кг картофеля. Удостоверьтесь, что числа, с которыми вы собираетесь выполнять арифметические действия, представлены в одном виде.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!
Как складывать десятичные дроби
Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
- Разряд должен находиться под разрядом, запятая под запятой.
Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Сложение дробей с равными знаменателями
Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.
Сложение дробей с разными знаменателями методом нахождения общего кратного
Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
- 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя.
 Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3. - Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.
- Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.
Сложение дробей методом умножения крест на крест
Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Как отнимать дроби с разными. Сложение и вычитание обыкновенных дробей
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти , а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)
В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)
Сложение смешанных чисел или смешанных дробей.

Сложение происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)
Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)
Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)
Ответ: весь торт съели.
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Калькулятор дробей
Введите две дроби:
| + — * : | |||||||
Сопутствующие разделы.
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
Сложение и вычитание обыкновенных дробей правило. Сложение дробей с целыми числами и разными знаменателями
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
В знаменателях принято оставлять произведение. Получаем:
Правила сложения дробей с разными знаменателями очень простые.
Рассмотрим правила сложения дробей с разными знаменателями по шагам:
1. Найти НОК (наименьшее общее кратное) знаменателей. Полученный НОК будет общим знаменателем дробей;
2. Привести дроби к общему знаменателю;
3. Сложить дроби, приведенные к общему знаменателю.
На простом примере научимся применять правила сложения дробей с разными знаменателями.
Пример
Пример сложения дробей с разными знаменателями.
Сложить дроби с разными знаменателями:
| 1 | + | 5 |
|---|---|---|
| 6 | 12 |
Будем решать по шагам.
1. Найти НОК (наименьшее общее кратное) знаменателей.
Число 12 делится на 6.
Отсюда делаем вывод, что 12 есть наименьшее общее кратное чисел 6 и 12.
Ответ: нок чисел 6 и 12 равен 12:
НОК(6, 12) = 12
Полученный НОК и будет общим знаменателем двух дробей 1/6 и 5/12.
2. Привести дроби к общему знаменателю.
В нашем примере привести к общему знаменателю 12 нужно только первую дробь, ведь у второй дроби знаменатель уже равен 12.
Разделим общий знаменатель 12 на знаменатель первой дроби:
2 есть дополнительный множитель.
Умножим числитель и знаменатель первой дроби (1/6) на дополнительный множитель 2.
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Сложение и вычитание дробей с помощью программы «Пошаговое решение математических задач». Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЗНАКОВЫЕ ЧИСЛА
ЗАДАЧИ
По завершении этого раздела вы должны уметь:
- Разложите числитель и знаменатель дроби на множители.
- Упростите алгебраические дроби.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
При изучении арифметики вам сказали, что дробные ответы всегда следует оставлять в сокращенной или упрощенной форме. Для дроби, до которой вы «уменьшили», разделив числитель и знаменатель на 4. Дробь нельзя уменьшить, потому что никакое число (кроме 1) не будет делить и числитель, и знаменатель. Упрощая дроби таким образом, вы использовали следующее определение.
Дробь в представляет собой упрощенную (или сокращенную) форму , если числитель и знаменатель не содержат общего множителя (кроме 1).
| Дробь, представленная в упрощенной форме, поскольку числитель 2 и знаменатель 3 не имеют общего делителя, кроме единицы. |
Для получения упрощенной формы дроби применяется следующее правило.
Чтобы упростить дробь , полностью разложите числитель и знаменатель, а затем разделите числитель и знаменатель на все общие множители.
| Дробь , однако, не в упрощенной форме, так как числитель и знаменатель имеют общий делитель 2. |
Затем разделите на общие делители, давая
| 7 9 деленный делитель само по себе равно 1. |
Теперь разделите на общий множитель (x + 2) как в числителе, так и в знаменателе, чтобы получить
Мы можем делить только общие множители, но не общие термины. |
| В таком выражении, как у некоторых учащихся, возникает соблазн разделить тройки. Обратите внимание, что это неверное , поскольку они являются терминами , а не факторами. |
Обратите внимание, что даже если мы смогли разложить на множители числитель и знаменатель, мы все равно не можем разделить, поскольку у них нет общих множителей. Данная дробь уже в упрощенном виде.
Тот факт, что для данной дроби может потребоваться любой из изученных вами методов факторинга, еще раз подчеркивает важность владения факторингом.
Решение Здесь вы можете использовать «пробы и ошибки» для числителя и «группировку» для знаменателя.
| Здесь (x + 2) — общий множитель, поэтому можно разделить и числитель, и знаменатель. |
Обратите внимание, что числитель 2x + 5 можно записать как (2x 4-5) * 1. Таким образом, при делении множителя (2x + 5) остается множитель 1. Таким образом, при делении множителя (2x + 5) остается множитель 1. |
Решение Этот тип проблемы требует особого внимания, так как является частой причиной ошибки. На первый взгляд множители могут быть ошибочно приняты за общие, или дробь может быть ошибочно принята за уже упрощенную. Обратите внимание, что факторы нельзя разделить, поскольку знаки не позволяют им быть идентичными. Если, однако, минус 1 факторизуется от одного из множителей, то есть подобные множители, и деление может быть выполнено.
| Любые множители в виде a — b и b — a являются отрицательными значениями друг друга, таким образом, 2x — 3 и 3 — 2x являются отрицательными значениями друг друга. |
Все это эквивалентные формы одного и того же выражения. Предпочтительной формой будет та, в которой используется наименьшее количество письменных знаков. Всегда проверяйте свой ответ, чтобы убедиться, что он эквивалентен форме, указанной в разделе ответов. |
УМНОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Числители и знаменатели всех умножаемых дробей.
- Определить и разделить на все общие множители.
- Запишите произведение в простейшей форме.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
— это определение произведения двух дробей. На словах это означает «умножить числитель на числитель и знаменатель на знаменатель». Вы использовали это правило много раз в арифметике, когда умножали дроби.
Однако помните, что все дробные ответы должны быть в упрощенной форме. Мы могли бы следовать приведенному выше определению, а затем упростить ответ, как в предыдущем разделе. Но с алгебраическими дробями это может привести к очень сложным выражениям. Следующее правило позволяет нам упрощать по мере умножения, поэтому ответ будет в упрощенной форме.
При умножении алгебраических дробей полностью разложите все числители и знаменатели, затем перед умножением разделите на все множители, общие для числителя и знаменателя.
Произведение остальных множителей числителя будет числителем ответа, а произведение остальных множителей знаменателя будет знаменателем ответа.
| Опять же, помните, что общие факторы должны быть совершенно одинаковыми. |
| Мы будем использовать точку * для обозначения умножения, поскольку использование X можно спутать с переменной x. |
| Обратите внимание, что (x + 2) и (2 + x) одинаковы, но (x — 4) и (4 — x) являются отрицательными значениями друг друга. Опять же, есть много возможных форм для окончательных ответов.  Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков. Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков. |
| В этой проблеме много факторов. Будь осторожен! |
ДЕЛЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Замените задачу на деление связанной с ней задачей на умножение.
- Деление алгебраических дробей.
Деление дробей определяется с помощью умножения.
Чтобы разделить, умножить на величину, обратную делителю.
Чтобы разделить одно алгебраическое выражение на другое инвертировать делитель и изменить операцию на умножение.
| Делитель следует за знаком. Не инвертируйте неправильную дробь. |
Если знаменатель не указан, считается, что он равен 1.
ПОИСК НАИМЕНЬШЕГО ОБЩЕГО ЗНАМЕНАТЕЛЯЦЕЛИПо завершении этого раздела вы должны уметь:
Правило сложения и вычитания дробей требует, чтобы объединяемые дроби имели одинаковый знаменатель. В качестве подготовки к выполнению этих операций мы теперь исследуем метод нахождения наименьшего общего знаменателя для любой группы дробей. общий знаменатель лот двух или более дробей представляет собой выражение, содержащее все множители знаменателя каждой дроби. Наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.
Ментальная арифметика позволит вам найти наименьший общий знаменатель для небольших чисел. Если попросить прибавить , то легко получить наименьший общий знаменатель 12. Если спросить, как мы получили 12, мы просто знаем, что 12 — это наименьшее число, которое делится и на 4, и на 6. Однако необходим более сложный метод. если числа больше или если дроби являются алгебраическими дробями. Пример 1 Найдите наименьший общий знаменатель для Решение Если бы у нас не было общего метода, эта задача потребовала бы значительного количества догадок или возможностей проверки.
Рассмотрим определение. Из него мы знаем, что общий знаменатель этих чисел должен содержать все множители каждого из них. Искомое число должно содержать (2)(2)(3), чтобы оно делилось на 12. Оно должно содержать (2)(7), чтобы делиться на 14, и так далее. Действуйте следующим образом:
Предыдущее обсуждение приводит к правилу получения наименьшего общего знаменателя для любого количества дробей, будь то числа или алгебраические выражения. Чтобы найти наименьший общий знаменатель для двух или более дробей:
При проверке второго знаменателя нам нужен дополнительный множитель (x — 2). Наименьший общий знаменатель равен (3x — 4)(2x + l)(x — 2).
Решение ЭКВИВАЛЕНТНЫЕ ДробиЦЕЛИПо завершении этого раздела вы должны уметь:
При дальнейшей подготовке к сложению и вычитанию дробей мы должны иметь возможность заменить заданную дробь дробью с новым знаменателем, не изменяя значение исходной дроби. называется фундаментальным принципом дробей . Анализируя это утверждение, мы видим две эквивалентные дроби и отмечаем, что числитель и знаменатель умножены на одно и то же ненулевое число a. Чтобы заменить дробь эквивалентной дробью , умножьте числитель и знаменатель на одно и то же ненулевое выражение.
Решение Поскольку новый знаменатель находится в факторизованной форме, при проверке мы видим, что первоначальный знаменатель (2x + 3) был умножен на множитель (x — 4). Следовательно, исходный числитель (x + 1) необходимо также умножить на множитель (x — 4), что даст
Решение Поскольку исходный знаменатель (x — 3) был умножен на (2) и (x + 1), исходный числитель (2x + 1) также необходимо умножить на (2) и ( х + 1).
СЛОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙЦЕЛИПо завершении этого раздела вы должны уметь:
Теперь мы готовы складывать алгебраические дроби, используя методы, описанные в двух предыдущих разделах. Следует вспомнить следующее правило из арифметики. Сумма двух или более дробей, имеющих одинаковый знаменатель, равна сумме числителей над их общим знаменателем. Обратите внимание, что это правило допускает только сумму дробей с одинаковым знаменателем. Чтобы сложить две или более дроби, выполните следующие действия:
Этот ответ в сокращенной форме.
Сумма равна
Мы можем использовать меньше письменных шагов, если заметим, что «общий знаменатель» означает, что все дроби имеют один и тот же знаменатель, а если у всех один и тот же знаменатель, то знаменатель необходимо написать только один раз.
ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙЦЕЛИПо завершении этого раздела вы должны уметь:
Вычитание определяется в терминах сложения, поэтому метод вычитания алгебраических дробей будет таким же, как сложение алгебраических дробей, описанный в предыдущем разделе. Вы скоро поймете, почему мы представили их отдельно. Разность любых двух дробей, имеющих один и тот же знаменатель, равна разнице их числителей над их общим знаменателем. Обратите внимание, что это правило совпадает с правилом сложения двух дробей с одинаковым знаменателем. Таким образом, шаги для вычитания дробей такие же, как и для сложения дробей. Чтобы вычесть дроби: Возникает очевидный вопрос: «Если эти две операции одинаковы, зачем изучать их по отдельности?» Ответ заключается в том, что вычитание порождает очень распространенную ошибку, которой ученик должен быть готов избежать.
Упомянутая ошибка часто возникает из-за того, что знак минус влияет на весь числитель второй дроби, а НЕ только на первый член.
Стрелка указывает на ошибку, наиболее часто допускаемую при вычитании дробей. Лучший способ избежать этого — всегда использовать круглые скобки , и вы вряд ли не сможете правильно изменить знак.
СЛОЖНЫЕ ДРОИЦЕЛИПо завершении этого раздела вы должны уметь:
Дроби определяются как указанное частное двух выражений. В этом разделе мы представим метод упрощения дробей, в которых числитель, знаменатель или оба они сами состоят из дробей. Такие фракции называются сложными фракциями . Таким образом, если числитель и знаменатель сложной дроби составлены из простых дробей, ее можно упростить, разделив числитель на знаменатель. Как правило, более эффективный метод упрощения сложной дроби включает использование фундаментального принципа дробей. Умножаем и числитель, и знаменатель на общий знаменатель всех отдельных дробей сложной дроби.
Мы будем использовать фундаментальный принцип, чтобы еще раз упростить LCD 3 и 4 равно 12. Таким образом,
УРАВНЕНИЯ С АЛГЕБРАИЧЕСКИМИ ДРОБЯМИЗАДАЧИПо завершении этого раздела вы сможете:
В главе 2 мы столкнулись с уравнениями, в которых есть дроби. Однако все эти дроби имели числовые знаменатели. Теперь обсудим уравнения, в знаменателях которых есть дроби с переменными. Метод решения этих уравнений будет таким же, как и в главе 2, но есть некоторые дополнительные предостережения, к которым вы должны быть готовы.
Чтобы освежить вашу память, здесь повторяются шаги решения таких уравнений. Основное отличие решения уравнений с арифметическими дробями от уравнений с алгебраическими дробями заключается в проверке. Процесс проверки будет заключаться не только в том, чтобы найти возможную ошибку, но и в том, чтобы определить, есть ли у уравнения ответ. Последняя возможность возникает потому, что алгебраические дроби умножаются на неизвестную величину. Эта неизвестная величина может быть на самом деле равна нулю, что сделает всю работу недействительной.
Поскольку деление на ноль невозможно, мы должны заключить, что x = 1 не является решением. А так как мы не ошиблись в вычислениях, то должны заключить, что это уравнение не имеет решения.
Таким образом, x = -5 является решением. Следовательно, 11 — это сумма, на которую был увеличен числитель. ОБЗОРКлючевые слова
Процедуры
Сложение и вычитание дробей – Математика для торговли: Том 1Дроби Эбигейл, Ханна и Наоми готовятся к промежуточному экзамену. Материал, который они должны изучить, состоит из 16 глав для чтения. Все трое понимают, что 16 глав — это много для каждого из них, поэтому они решают учиться более эффективно. Они составляют план, в котором каждый из них читает определенное количество глав, а затем резюмирует его для двух других. Они будут делиться заметками, и каждый найдет онлайн-видео, соответствующее их конкретному набору глав. Теперь главы не создаются одинаково. Некоторые из них довольно легкие, а другие намного сложнее. Их цель — равномерно распределить нагрузку между тремя из них. Помните, что есть 16 глав. У Эбигейл самое большое количество глав, которые нужно пройти — 6. У Ханны — 5, а у Наоми — только 4. Если бы вы сложили их, вы бы заметили, что получается только 15 глав. Последняя глава книги посвящена устранению неполадок в электрических системах, и ученики решают, что они пройдут ее вместе. Мы можем представить каждую из их рабочих нагрузок в виде части целого: [латекс]\БОЛЬШОЙ\текст{У Эбигейл}\dfrac{6}{16}[/латекс] [латекс]\БОЛЬШОЙ\текст{У Ханны}\dfrac{5}{16}[/латекс] [латекс]\БОЛЬШОЙ\текст{У Наоми}\dfrac{4}{16}[/латекс] Что, если сложить эти дроби? Это будет выглядеть примерно так: [латекс]\БОЛЬШОЙ\dfrac{6}{16}+\dfrac{5}{16}+\dfrac{4}{16}=?[/latex] Вы заметите, что все числители разные, а знаменатели одинаковые (16). При сложении или вычитании дробей знаменатели должны совпадать. Мы называем это наличием общего знаменателя. Итак, чтобы получить ответ на поставленный выше вопрос, нужно просто сложить все числители. Обратите внимание, что знаменатель в окончательном ответе такой же, как и в складываемых дробях. К концу ученики пройдут 15 из 16 глав по отдельности, а последнюю главу они пройдут вместе. Концепция сложения дробей с общими знаменателями достаточно проста, и мы сделали достаточно, чтобы складывать целые числа, поэтому рассматривать примеры на этом этапе, возможно, не стоит (но если вам нужен обзор, см. Сложение целых чисел). Вместо этого мы запишем несколько примеров сложения дробей, чтобы вы могли понять идею. [латекс]\БОЛЬШОЙ\dfrac{1}{8}+\dfrac{2}{8}=\dfrac{3}{8}[/latex] [латекс]\БОЛЬШОЙ\dfrac{5}{16}+\dfrac{6}{16}=\dfrac{11}{16}[/latex] [латекс]\БОЛЬШОЙ\dfrac{13}{32}+\dfrac{11}{32}=\dfrac{24}{32}[/latex] Вы ничего не заметили в ответе на последний вопрос? Его можно уменьшить. [латекс]\БОЛЬШОЙ\dfrac{24}{32}\longrightarrow\dfrac{2}{3}[/latex] Прежде чем мы продолжим работу с дробями, самое время сказать, что при работе с дробями мы обычно хотим дать ответ в самом низком выражении. Как насчет вычитания дробей? Ну, по тому же принципу: у вас должен быть общий знаменатель, а затем вы вычитаете числители. Вот несколько примеров вычитания дробей: [латекс]\БОЛЬШОЙ\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}[/latex] [латекс]\БОЛЬШОЙ\dfrac{9}{16}-\dfrac{5}{16}=\dfrac{4}{16}\longrightarrow\dfrac{1}{4}[/latex] [латекс]\БОЛЬШОЙ\dfrac{27}{32}-\dfrac{14}{32}=\dfrac{13}{32}[/latex] Сейчас мы немного усложним задачу. Наши примеры сложения и вычитания дробей довольно просты из-за того, что знаменатели одинаковы. Более сложная ситуация связана с добавлением или вычитанием дробей, имеющих разные знаменатели. Взгляните на следующий пример: [латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{3}{8}=?[/latex] Мы не можем просто сложить числители и знаменатели, так как это просто не сработает. Взгляните на два круга, нарисованные ниже. Один разделен на 2 части, а другой на 8 частей. Вы заметили что-нибудь о размерах деталей?
Вы заметите, что части в круге из 2 частей намного больше, чем в круге из 8 частей. Идея состоит в том, чтобы сделать так, чтобы добавляемые детали были одинакового размера. Если мы каким-то образом доберемся до этой точки, тогда все готово, и мы можем сложить две дроби. Это называется поиском общего знаменателя, и чаще всего мы пытаемся найти наименьший общий знаменатель . Наименьший общий знаменатель : Наименьшее число, в которое могут входить два знаменателя. Взгляните на приведенное ниже уравнение. Один из знаменателей равен 2, а другой равен 8,9.0003 [латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{3}{8}=?[/latex] Процесс здесь аналогичен тому, как мы приводили дроби к их наименьшему члену в предыдущем разделе, только на этот раз мы будем увеличивать по крайней мере один из знаменателей, а иногда мы будем увеличивать оба, пока не найдем тот, который общий. Мы ищем число, в которое оба знаменателя могут входить поровну. Мы определили, что 8 будет нашим общим знаменателем, а это значит, что одна из дробей уже готова. А как насчет 1 на 2 или наполовину? Мы должны превратить половину в дробь с 8 в знаменателе. Как мы подсчитали выше, 2 входит в число 8 четыре раза. [латекс]\БОЛЬШОЙ2\times4=8[/латекс] Это хорошо для знаменателя, но как насчет числителя? Итак, что бы мы ни сделали с одной частью дроби, мы должны сделать то же самое с другой частью. Это оставляет дробь с тем же значением. Затем мы также должны умножить 1 на 4. [латекс]\БОЛЬШОЙ1\times4=4[/латекс] Если бы мы хотели сделать все за один шаг, это выглядело бы примерно так: Теперь у нас есть кое-что, с чем мы можем работать. Вернитесь к исходному уравнению и замените [latex]\dfrac{1}{2}[/latex] на [latex]\dfrac{4}{8}[/latex]. [латекс]\БОЛЬШОЙ\dfrac{4}{8}+\dfrac{3}{8}=\dfrac{7}{8}[/latex] Хорошо, это работает для сложения дробей, но как насчет вычитания дробей? Ну, вычитание дробей происходит по тому же принципу: если знаменатели не совпадают, то мы должны сначала найти общий знаменатель, прежде чем вычитать две дроби. Вычислите следующее: [латекс]\НАИБОЛЬШИЙ\dfrac{7}{8}-\dfrac{13}{16}=[/latex] Шаг 1 : Найдите общий знаменатель. Это может стать немного сложнее, когда числа начинают расти. По мере того, как вы лучше знакомитесь с закономерностями в числах, ответы будут даваться легче. Вопрос, который мы задаем прямо сейчас, звучит так: «В какое число могут входить и 8, и 16 без остатка?» Мы могли бы даже начать с проверки того, может ли меньший знаменатель войти в больший знаменатель. В данном случае так и есть. Дробь с общим знаменателем 16 уже готова, но нам нужно работать с дробью со знаменателем 8. Шаг 2 : Умножьте числитель и знаменатель ⅞ на 2, чтобы получить дробь общий знаменатель 16. Шаг 3 : Вычтите новые версии дробей. [латекс]\БОЛЬШОЙ\dfrac{14}{16}-\dfrac{13}{16}=\dfrac{1}{16}[/latex] Ответьте на следующие практические вопросы и посмотрите видеоответы. Не забудьте поставить каждый ответ в самом низком выражении или в смешанном числе, если это необходимо. [латекс]\БОЛЬШОЙ\dfrac{3}{16}+\dfrac{5}{8}=[/латекс] [латекс]\БОЛЬШОЙ\dfrac{5}{8}-\dfrac{5}{16}=[/латекс] [латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{7}{8}=[/латекс] [латекс]\БОЛЬШОЙ2\dfrac{1}{2}+1\dfrac{7}{8}=[/латекс] Минуточку! Этот последний вопрос поднял его на ступеньку выше, добавив смешанные числа. Я знаю, что вы уже посмотрели видеоответ, но давайте сделаем шаг назад и пройдемся по сложению и вычитанию смешанных чисел. Мы начнем с краткого объяснения. Проблема, с которой мы сталкиваемся при сложении или вычитании смешанных чисел, заключается в том, что смешанное число состоит из двух отдельных частей: есть целое число, а есть дробь. При добавлении чисел это может быть просто, например: .[латекс]\БОЛЬШОЙ4\dfrac{3}{8}+3\dfrac{2}{8}=7\dfrac{5}{8}[/latex] Довольно просто, не так ли? Вы просто складываете два целых числа, а затем складываете дроби. Это работает довольно хорошо. Но как насчет ситуации, подобной следующему примеру? [латекс]\БОЛЬШОЙ4\dfrac{5}{8}+3\dfrac{4}{8}=?[/latex] Вы видите проблему? Проблема (на самом деле это не проблема) в том, что когда мы складываем дроби, мы получаем большее число в числителе, чем в знаменателе. [латекс]\БОЛЬШОЙ4\dfrac{5}{8}+3\dfrac{4}{8}=7\dfrac{9}{8}[/latex] Решение состоит в том, чтобы заменить часть ответа на неправильную дробь смешанным числом, а затем добавить его к целой части ответа. [латекс]\БОЛЬШОЙ\dfrac{9}{8}\longrightarrow1\dfrac{1}{8}[/latex] Возьмите 7 и прибавьте к смешанному числу, чтобы получить окончательный ответ. [латекс]\БОЛЬШОЙ7+1\dfrac{1}{8}=8\dfrac{1}{8}[/латекс] Хорошо, это кажется довольно простым, но как насчет вычитания? Что ж, мы следуем тем же правилам. Взгляните на следующий пример: [latex]\LARGE8\dfrac{7}{8}-6\dfrac{3}{8}=?[/latex] Процедура похожа на сложение дробей, но вместо сложения мы вычитаем . Мы можем разбить его на две части. Начнем с вычитания целых чисел, а затем вычтем часть дробей. Шаг 1 : Вычтите целые числа. [латекс]\НАИБОЛЬШИЙ8-6=2[/латекс] Шаг 2 : Вычтите дробную часть уравнения. [латекс]\БОЛЬШОЙ\dfrac{7}{8}-\dfrac{3}{8}=\dfrac{4}{8}\стрелка вправо\dfrac{1}{2}[/latex] Шаг 3 : Соберите все воедино. [латекс]\БОЛЬШОЙ8\dfrac{7}{8}-6\dfrac{3}{8}=2\dfrac{4}{8}\rightarrow2\dfrac{1}{2}[/latex] Хорошо, не слишком сложно, правда? Но взгляните на следующий пример и посмотрите, сможете ли вы понять проблему, с которой мы столкнемся, когда будем ее решать. [latex]\LARGE5\dfrac{2}{8}-3\dfrac{7}{8}=?[/latex] Проблема возникает не тогда, когда вы вычитаете целые числа, а когда вы вычитаете дроби. [латекс]\БОЛЬШОЙ\dfrac{2}{8}-\dfrac{7}{8}=?[/latex] В итоге мы получим ответ меньше нуля. Это не сработает для нас. Итак, как мы решим проблему? Что ж, ответ заключается в заимствовании, а то, что мы заимствуем, — это целое число, 5. Скажем так, мы заимствуем 1 из 5. В результате у нас останется 4, а дальше что? Взгляните на следующую логику. [латекс]\БОЛЬШОЙ5=4+1[/латекс] [латекс]\БОЛЬШОЙ1=\dfrac{8}{8}[/латекс] Если мы продолжим и разобьем 5 на 4 и 1 , а затем разделить эту 1 на части по 8, у нас есть гораздо больше восьмых для работы. [латекс]\БОЛЬШОЙ5\dfrac{2}{8}=4+\dfrac{8}{8}+\dfrac{2}{8}=4\dfrac {10}{8}[/latex] Теперь у нас есть числа, с которыми мы можем работать в исходном вопросе. [латекс]\БОЛЬШОЙ4\dfrac{10}{8}-3\dfrac{7}{8}=?[/latex] Выполняем те же действия, что и раньше. Шаг 1 : Вычтите целые числа. [латекс]\НАИБОЛЕЕ4-3=1[/латекс] Шаг 2 : Вычтите дробную часть уравнения. [латекс]\БОЛЬШОЙ\dfrac{10}{8}-\dfrac{7}{8}=\dfrac{3}{8}[/latex] Шаг 3 : Соберите все вместе. [латекс]\БОЛЬШОЙ4\dfrac{10}{8}-3\dfrac{7}{8}=1\dfrac{3}{8}[/latex] Сложите или вычтите следующие смешанные числа, убедившись, что ваш ответ представлен в самом низком выражении. Посмотрите видеоответы в конце, чтобы узнать, как вы справились. [латекс]\БОЛЬШОЙ7\dfrac{3}{16}+4\dfrac{5}{16}=[/латекс] [латекс]\БОЛЬШОЙ2\dfrac{7}{16}+3\dfrac{7}{8}=[/латекс] [латекс]\БОЛЬШОЙ8\dfrac{27}{32}-1\dfrac{15}{32}=[/латекс] [латекс]\БОЛЬШОЙ6\dfrac{5}{16}-5\dfrac{5}{8}=[/латекс] Как вычитать дроби с разными знаменателями Вычитание дробей, особенно с разными знаменателями, может показаться сложным на первый взгляд. Во-первых, нам нужно понять состав дроби. Здесь есть две части – числитель и знаменатель, разделенные разделительной чертой. В знаменателе находится нижняя цифра. Это показывает нам, на сколько равных частей было разделено одно целое. Числитель является верхней цифрой и показывает, сколько частей целого присутствует. Чтобы успешно отделить одну дробь от другой, нужно добиться того, чтобы целое, с которым мы имеем дело, в обоих случаях делилось на одинаковое количество равных частей, т. е. чтобы знаменатели были одинаковыми. Есть несколько быстрых приемов, которые можно использовать при вычитании дробей с разными знаменателями. Ниже мы объясняем традиционный метод, поскольку именно его вам нужно будет применить, когда вас попросят показать свои работы на любом официальном экзамене. Одни и те же правила применяются при работе с правильными дробями (где числитель меньше знаменателя) или неправильными дробями (где числитель больше знаменателя). 4 простых шага, как вычитать дроби с разными знаменателями:Шаг 1: Найдите наименьший общий знаменательНаименьший общий знаменатель (НОД) — это наименьшее общее кратное двух знаменателей, с которыми вы работаете. Например, если нас попросили вычесть 2/3 из 2/6, мы знаем, что 6 кратно 3, поэтому 6 — это наш LCD. Шаг 2: Найдите эквивалентную дробьПосле того, как вы нашли ЖК-дисплей, вам нужно сохранить значение ваших дробей прежним. Таким образом, при изменении знаменателя вам нужно применить то же изменение к числителю. Используя приведенный выше пример, чтобы заменить знаменатель на 6, мы умножаем 3 на 2. Чтобы сохранить дробь равного значения, мы также должны умножить 2 (числитель) на 2. Это дает нам эквивалент дроби 4 /6. Повторите этот процесс и для второй фракции. В нашем примере знаменатель уже равен 6, поэтому никаких изменений не требуется. Теперь у нас есть пересмотренное уравнение 4/6 — 2/6. Шаг 3: Вычтите новые числителиСледующий этап прост: просто вычтите числители, которые есть в вашем новом уравнении. В этом случае 4 — 2 = 2, Возьмите полученную цифру и поместите ее над общим знаменателем. Это дает нам 2/6. Шаг 4: При необходимости упростите ответПоследний шаг – по возможности упростить дробь. Для этого вам нужно найти наибольший общий множитель, общий для обеих частей дроби, и разделить их на него. В случае 2/6 наибольший общий множитель равен 2. Поскольку 2 ÷ 2 = 1, а 6 ÷ 2 = 3, наша упрощенная дробь равна 1/3. 2/3 — 2/6 = 1/3 Примеры вопросовНиже вы найдете два примера вопросов, в которых вам предлагается вычесть дроби с разными знаменателями. Первое выражается в виде стандартного уравнения, второе — в виде более сложной словесной задачи. Пример вопроса 1Сколько будет 5/6 минус 13/25? Начните с поиска ЖК-дисплея. В этом примере это не так просто, поэтому вам может быть полезно записать кратные наибольшему текущему знаменателю, чтобы помочь вам: 25, 50, 75, 100, 125, 150… Теперь мы можем видеть, что первое кратное 25 делится на 6 равно 150, так что это наш ЖК-дисплей. Затем нам нужно найти наши эквивалентные дроби: 6 x 25 = 150, поэтому нам нужно использовать то же значение, чтобы умножить числитель, что даст 5 x 25 = 125. Таким образом, наша первая эквивалентная дробь будет 125/150. Теперь перейдем ко второй: 25 х 6 = 150 и 13 х 6 = 78. Наша вторая эквивалентная дробь 78/150. Вычтите числители и поместите результат на ЖК-дисплей: 125/150 — 78/150 = 47/150. Эта фракция уже имеет простейшую форму. Ответ: 5/6 минус 13/25 = 47/150 Пример вопроса 2Эмма готовится к марафону и поставила перед собой цель пробежать к концу недели. В понедельник она пробегает 7/15 дистанции. В среду она пробегает 4/5 дистанции. Насколько дальше пробежала Эмма в среду по сравнению с понедельником? Чтобы решить эту задачу, нам нужно вычесть расстояние, которое Эмма пробежала в понедельник, из того, сколько она пробежала в среду, поэтому наше уравнение будет выглядеть так: 4/5 — 7/15. Затем мы находим наш ЖК-дисплей, который, как мы видим, равен 15. Мы находим эквивалент нашей первой дроби, умножая обе части на одно и то же значение: 5 x 3 = 15 и 4 x 3 = 12. Наша эквивалентная дробь поэтому 12/15. Так как во второй дроби наш знаменатель уже равен 15, здесь никаких изменений не требуется. Теперь мы можем вычесть наши числители (12 — 7 = 5) и поставить наш ответ над знаменателем: 5/15. Наконец, мы идентифицируем наибольший общий делитель 5 и 15 как 5 и делим обе части дроби для упрощения: 5 ÷ 5 = 1 и 15 ÷ 5 = 3. Ответ: 4/5 минус 7/15 = 1/3 Калькулятор дробей Правила выражений с дробями:Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями. Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью Математические символы
|
 В результате мы почти найдем ответ;
В результате мы почти найдем ответ;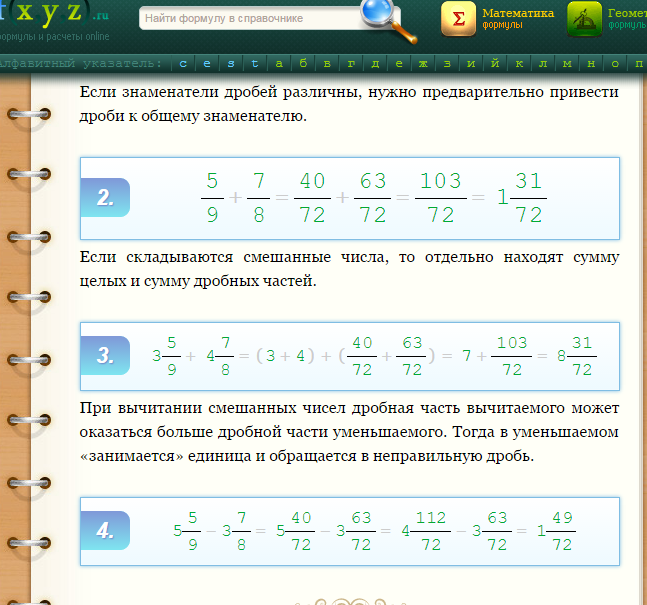
 Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше; Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
