Конгруэнтность это в геометрии: Что такое конгруэнтность, чем она отличается от равенства, и где ошибка в Конституции США? / Хабр

Конгруэнтность

В геометрии две фигуры или объекта конгруэнтны, если они имеют одинаковую форму и размер. Также если одна из них имеет ту же форму и размер, что и зеркальное отражение другой.

Более формально, два набора точек называются конгруэнтными тогда и только тогда, когда один из них может быть преобразован в другой с помощью изометрии. Для изометрии используются жесткие движения.

Это означает, что один объект можно переместить и отразить (но не изменить его размер) так, чтобы он точно совпал с другим объектом. Так, две разные плоские фигуры на листе бумаги конгруэнтны, если мы можем их вырезать и затем полностью совместить. Переворачивать бумагу разрешается.

Конгруэнтные многоугольники — это многоугольники, которые если сложить обычный многоугольник пополам, то получится конгруэнтный многоугольник.

Две геометрические фигуры конгруэнтны, если одну из них можно переместить или повернуть так, чтобы она точно поместилась на место другой.

Если один из объектов должен изменить свой размер, два объекта не являются конгруэнтными: их просто называют похожими.

Если две фигуры или объекта конгруэнтны, они имеют одинаковую форму и размер; но их можно повернуть, переместить, зеркально отобразить (отразить) или перевести так, чтобы одна точно соответствовала другой.

Пример конгруэнтности. Два треугольника слева конгруэнтны, а третий подобен им. Последний треугольник не похож и не конгруэнтен ни одному из остальных. Обратите внимание, что конгруэнтность позволяет изменять некоторые свойства, такие как расположение и ориентация, но оставляет неизменными другие, такие как расстояние и углы. Неизменные свойства называются инвариантами.

Примеры

• все квадраты с одинаковой длиной сторон конгруэнтны.
• все равносторонние треугольники с одинаковой длиной сторон конгруэнтны.

Тесты на конгруэнтность

• Два угла и сторона между ними одинаковы у двух треугольников (конгруэнтность ASA)
• Два угла и сторона, не находящаяся между ними, одинаковы у обоих треугольников (конгруэнтность AAS)
• Все три стороны обоих треугольников одинаковы (конгруэнтность SSS)
• две стороны и угол между ними делают два треугольника конгруэнтными (конгруэнтность SAS)

Как мы можем получить новые конгруэнтные фигуры?

У нас есть достаточно много возможностей, несколько правил, чтобы сделать новые фигуры конгруэнтными исходным.

• Если мы сдвинем геометрическую фигуру в плоскости, то получим фигуру, конгруэнтную исходной.
• Если мы вращаем, а не сдвигаем, то также получаем фигуру, конгруэнтную исходной.
• Даже если мы возьмем зеркальное отражение исходной формы, то все равно получим конгруэнтную форму.
• Если мы объединим эти три действия одно за другим, то все равно получим конгруэнтные фигуры.
• Больше конгруэнтных фигур не существует. Более точно, это означает, что если фигура конгруэнтна исходной, то ее можно достичь тремя действиями, описанными выше.

Отношение, что фигура конгруэнтна другой фигуре, имеет три известных свойства.

• Если оставить исходную форму на прежнем месте, то она будет конгруэнтна самой себе. Это поведение, это свойство называется рефлексивностью.

Например, если вышеуказанный сдвиг не является правильным сдвигом, а только сдвигом, делающим движение длиной ноль. Или, аналогично, если вышеуказанный поворот не является правильным поворотом, а только поворотом на угол ноль.

• Если фигура конгруэнтна другой фигуре, то эта другая фигура также конгруэнтна исходной. Такое поведение, такое свойство называется симметрией.

Например, если мы сдвинем назад, или повернем назад, или зеркально отразим новую форму по отношению к исходной, то исходная форма будет конгруэнтна новой.

• Если форма C конгруэнтна форме B, а форма B конгруэнтна исходной форме A, то форма C также конгруэнтна исходной форме A. Такое поведение, такое свойство называется транзитивностью.

Например, если мы применим сначала сдвиг, а затем поворот, то полученная новая форма все равно будет конгруэнтна исходной.

Известные три свойства, рефлексивность, симметрия и транзитивность,

вместе составляют понятие эквивалентности. Следовательно, свойство конгруэнтности является одним из видов отношения эквивалентности между фигурами плоскости.

Вопросы и ответы

В: Что означает конгруэнтность двух фигур в геометрии?

О: Две фигуры конгруэнтны в геометрии, если они имеют одинаковую форму и размер, или если одна из них имеет ту же форму и размер, что и зеркальное отражение другой.

В: Как два набора точек называются конгруэнтными?

О: Два набора точек называются конгруэнтными тогда и только тогда, когда один из них может быть преобразован в другой с помощью изометрии.

В: Для чего в изометрии используются жесткие движения?

О: Жесткие движения используются в изометрии для изменения положения, поворота или отражения геометрических фигур без изменения их размера, чтобы они точно совпадали с другими объектами.

В: Могут ли две фигуры быть конгруэнтными, если одна из них должна изменить свой размер, чтобы совпасть с другой?

О: Нет, если один из объектов должен изменить свой размер, чтобы совпасть с другим, то эти два объекта не являются конгруэнтными, но называются похожими.

В: Что можно сказать о конгруэнтности двух разных плоских фигур на листе бумаги?

О: Две разные плоские фигуры на листе бумаги являются конгруэнтными, если мы можем их вырезать и затем полностью совместить, при необходимости перевернув бумагу.

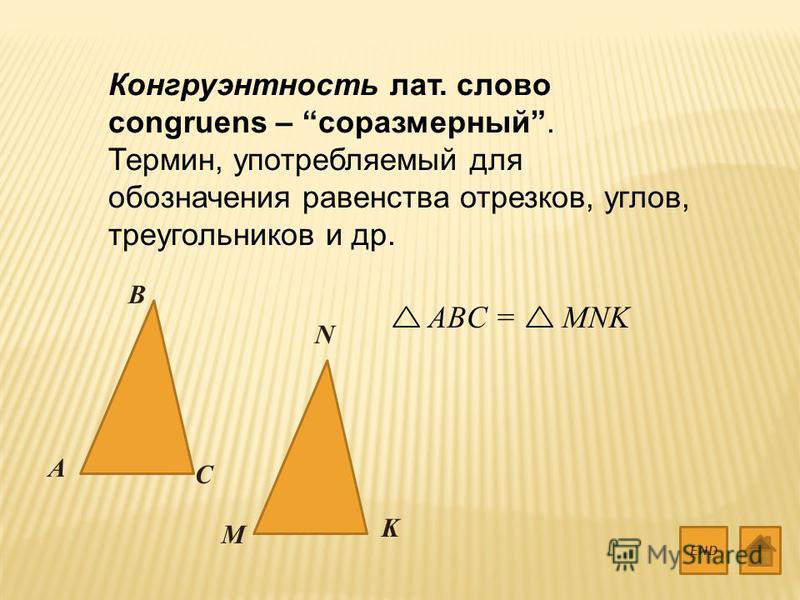
В: Что такое конгруэнтные многоугольники?

О: Конгруэнтные многоугольники — это многоугольники, которые можно сложить пополам и получить другой правильный многоугольник, который также является конгруэнтным.

В: Что является критерием для того, чтобы два объекта назывались конгруэнтными в геометрии?

О: Критерием того, что два объекта могут называться конгруэнтными в геометрии, является то, что один объект можно переместить, повернуть или отразить так, чтобы он точно совпадал с другим объектом без изменения его размера.

Автор

Alegsaonline.com — Конгруэнтность — Leandro Alegsa — 2022-01-18 18:30:02 — url: https://ru.alegsaonline.com/art/22523

Библиографические ссылки

— web.cortland.edu — «Oxford Concise Dictionary of Mathematics, Congruent Figures»

Конгруэнтность (геометрия)

В геометрии две фигуры или объекты считаются конгруэнтными, если они имеют одинаковую форму и размер или если один из них имеет ту же форму и размер, что и зеркальное отражение другого.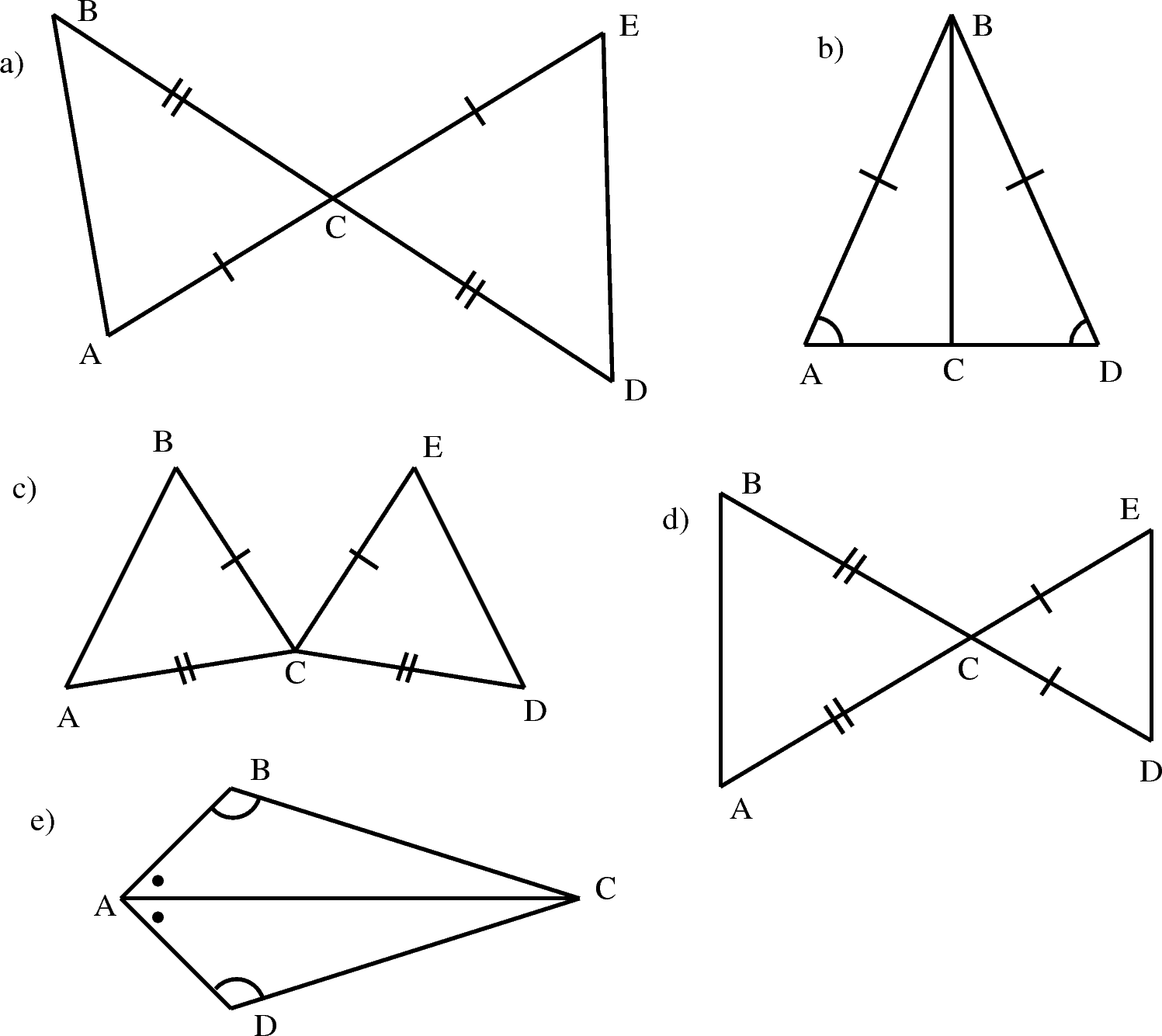 ^[1]

Более формально два множества точек называются конгруэнтными тогда и только тогда, когда одно может быть преобразовано в другое с помощью изометрии , т. е. комбинации жестких движений , а именно переноса , вращения и отражения . Это означает, что любой объект можно перемещать и отражать (но не изменять размер), чтобы он точно совпадал с другим объектом. Поэтому две различные плоские фигуры на листе бумаги конгруэнтны, если их можно вырезать, а затем полностью сопоставить. Разрешается переворачивать бумагу.

В элементарной геометрии слово конгруэнтный часто используется следующим образом. ^[2] Слово равный часто используется вместо конгруэнтного для этих объектов.

В этом смысле конгруэнтность двух плоских фигур означает, что их соответствующие характеристики «конгруэнтны» или «равны», включая не только их соответствующие стороны и углы, но также их соответствующие диагонали, периметры и площади.

Родственное понятие подобия применяется, если объекты имеют одинаковую форму, но не обязательно имеют одинаковый размер.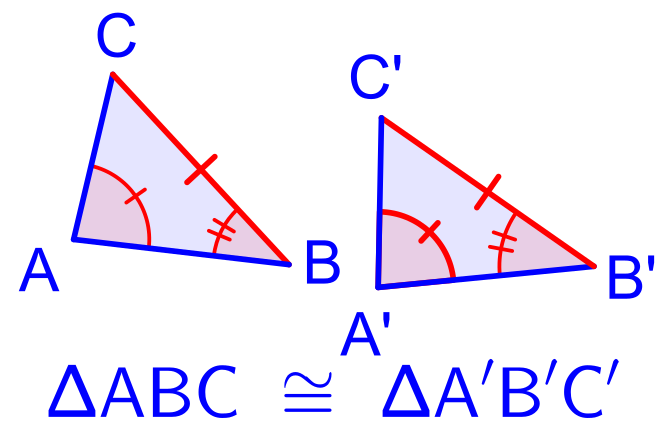

(Большинство определений рассматривают конгруэнтность как форму подобия, хотя меньшинство требует, чтобы объекты имели разные размеры, чтобы их можно было квалифицировать как похожие.)

Чтобы два многоугольника были конгруэнтными, они должны иметь одинаковое количество сторон (и, следовательно, равное количество — одинаковое количество — вершин). Два многоугольника с n сторонами конгруэнтны тогда и только тогда, когда каждый из них имеет численно идентичные последовательности (даже если по часовой стрелке для одного многоугольника и против часовой стрелки для другого) сторона-угол-сторона-угол-… для n сторон и n углов.

---

Пример конгруэнтности. Два треугольника слева равны, а третий подобен им. Последний треугольник не конгруэнтен и не похож ни на один из других. Конгруэнтность позволяет изменять некоторые свойства, такие как расположение и ориентация, но оставляет неизменными другие, такие как расстояния и углы . Неизменяемые свойства называются инвариантами .

Эта диаграмма иллюстрирует геометрический принцип конгруэнтности треугольника угол-угол-сторона: даны треугольник ABC и треугольник A’B’C’, треугольник ABC конгруэнтен треугольнику A’B’C’ тогда и только тогда, когда: угол CAB конгруэнтен углу C’A’B’, а угол ABC равен углу A’B’C’, а BC равен углу B’C’. Обратите внимание, что метки штриховки используются здесь, чтобы показать равенство углов и сторон.

Оранжевый и зеленый четырехугольники конгруэнтны; синий цвет им не соответствует. Все три имеют одинаковый периметр и площадь . (Порядок сторон синего четырехугольника «смешанный», в результате чего два внутренних угла и одна из диагоналей не совпадают.)

Форма треугольника определяется с точностью до конгруэнтности заданием двух сторон и угла между ними (SAS), двух углов и стороны между ними (ASA) или двух углов и соответствующей прилежащей стороны (AAS). Однако указание двух сторон и прилежащего угла (SSA) может дать два различных возможных треугольника.

Конгруэнтность | математика | Британника

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Связанный контент

Конгруэнтность и подобие | Определения и примеры

Автор:

Malcolm McKinsey

11 января 2023 г.

Проверено

Пол Маццола грубость и сходство?

Все конгруэнтные фигуры подобны, но не все подобные фигуры конгруэнтны. Конгруэнтность означает, что два объекта (будь то двумерные или трехмерные) идентичны по размеру и форме. Все в них — их углы, длины сторон, габаритные размеры — идентичны. Подобные   фигурки  имеют одинаковую форму и пропорции, но не обязательно одного размера.

Конгруэнтность

Два объекта могут иметь одинаковый размер и форму, но не иметь одинаковой ориентации. Они по-прежнему конгруэнтны, как морские звезды, повернутые в разные стороны.

Или рассмотрим шахматные фигуры, в которых один конь стоит на высокой полке, а другой — на нижней полке. Тот факт, что они находятся в разных плоскостях в трех измерениях, не исключает их конгруэнтности. Они по-прежнему совпадают.

В геометрии конгруэнтные фигуры  обладают тремя свойствами:

1. Одинаковый размер

2. Одинаковая форма

3. Соответствующие части Грунт

Именно поэтому в геометрических доказательствах мы иногда видим CPCFC, что означает «соответствующие части конгруэнтных фигур конгруэнтны».

Подобие

Подобие  означает одинаковую форму и пропорции, но не обязательно одинаковый размер. Углы подобных фигур будут равны, но длины сторон обычно не равны.

Пары конгруэнтных фигур автоматически подобны, но это отношение не работает в обратную сторону. Все конгруэнтные фигуры подобны, но не все подобные фигуры конгруэнтны.

Оба прямоугольника имеют одинаковые пропорции. Все круги подобны. Однако ни пара прямоугольников, ни окружностей не являются конгруэнтными. Только квадраты, будучи конгруэнтными, еще и подобны друг другу.

Использование конгруэнтности и подобия

Знание свойств конгруэнтности и подобия позволяет использовать их в доказательствах. Вы можете установить отношения между соответствующими частями двух подобных фигур.

Нарисуйте два прямоугольника, один размером 5 см x 3 см , а другой размером 2,5 см x 1,5 см.

Здесь отношения ширины к длине одинаковы:

Соотношения соответствующих частей также одинаковы:

Используя эти отношения и конгруэнтность углов, вы знаете, что формы подобны.