широкая теория . Кислый виноград. Исследование провалов рациональности
Теперь я хочу перейти к изучению более существенных коннотаций рациональности. Сказанное ранее не мешает нам говорить о самоубийстве, убийстве или геноциде как о рациональном поведении. Точно так же не было приведено никаких доводов в пользу того, чтобы исключить из области рационального танец для вызывания дождя у хопи, изучение гороскопа перед тем, как инвестировать в ценные бумаги, или решение вернуться домой, если дорогу перебежала черная кошка. Если говорить строго логически, существует и такая возможность, что весь мир участвует в заговоре, чтобы помешать мне добиться цели, и в слабом смысле, вероятно, для меня было бы вполне рационально действовать на этом основании. Однако ясно, что этот смысл слишком слаб. Нам требуется более широкая теория рациональности, которая выходит за рамки чисто формальных соображений предыдущего раздела и позволяет внимательно присмотреться к существу желаний и убеждений, которые участвуют в действии.
Мы хотим иметь возможность сказать, что действовать рационально значит действовать непротиворечиво на основании убеждений и желаний, которые являются не только непротиворечивыми, но и рациональными.
С другой стороны, не стоит до такой степени расширять понятие рациональности, чтобы оно охватывало все положительные свойства, которые нам хочется придать нашим убеждениям и желаниям. Я утверждаю, что между слабой теорией рациональности и полной теорией истины и блага имеется место для широкой теории рациональности, а также потребность в ней. Заявить, будто истинность является необходимым условием рациональных убеждений, значит просить слишком много; но заявить, что достаточно непротиворечивости, значит запросить слишком мало. То же, пускай и более спорно, относится к рациональным желаниям: требование непротиворечивости слишком слабое, требование этического блага – слишком сильное.
Я предлагаю оценивать широкую рациональность убеждений и желаний, глядя на то, как они формируются.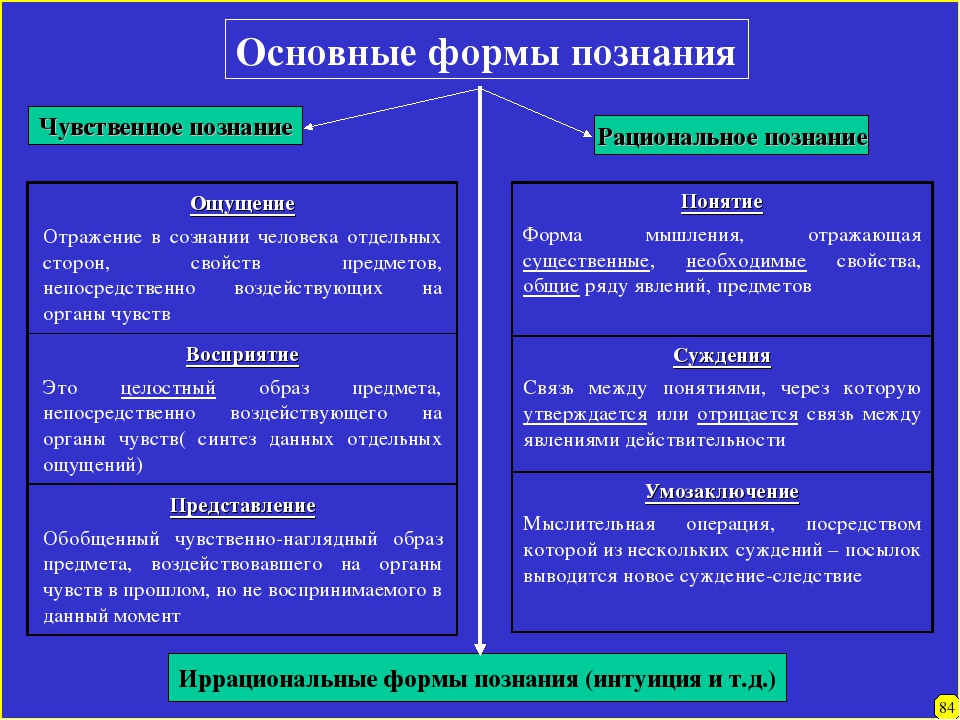
Рассмотрим сначала убеждения и их формирование. Ясно, что убеждение может быть истинным и при этом нерациональным, рациональным и при этом неистинным. Рациональность убеждений (будучи взята в своей сути) затрагивает отношения не между убеждениями и миром, но между убеждениями и имеющимися фактами. Более того, как подробнее говорится в главе IV, утверждение о том, что убеждение рационально, должно основываться не на сравнении фактов с убеждениями, а на изучении его действительной каузальной истории, ведь человек нерациональным путем может прийти к убеждению, которое также окажется фундированным в фактах. Кроме того, недостаточно сказать, что убеждение рационально, потому что вызвано фактами, которые делают рациональной веру в него, поскольку в конкретном случае оно вполне может вызываться фактами недолжным образом, например через механизм компенсирующих ошибок. Все это перекликается во многих аспектах с обсуждением в разделе I.
Положительно охарактеризовать рациональные убеждения можно через отсылку к понятию суждения, определяемому как способность синтезировать обширную и весьма разрозненную информацию, которая имеет более или менее четкое отношение к решаемой проблеме, не приписывая ни одному элементу или группе элементов в составе недолжной важности. Ясно, что определение несколько бесполезно, но в реальности этого феномена сомневаться не приходится. Все мы знаем людей, у которых есть это качество, и людей, которые его лишены. При некоторых занятиях без него невозможно обойтись, и те, у кого его нет, вскоре оказываются из них исключены. Крайние случаи – конкурентный рынок, на котором фирмы, управляемые людьми без способности суждения, быстро становятся банкротами, и война, где военачальники и солдаты, лишенные ее, подвергаются большому риску. В определенной степени это также верно и в отношении политиков, для которых способность суждения и здравый смысл, в дополнение к чистому упорству и некоторой наработанной бесчувственности, гораздо важнее ума в его традиционном понимании.
Однако вскоре окажется, что бойко говорить об «имеющихся фактах» недостаточно, поскольку встает важнейший вопрос о том, какое именно количество фактов следует рационально накопить, прежде чем прийти к убеждению. Этот вопрос допускает разные ответы в зависимости от цели, с которой в дальнейшем будет использоваться данное убеждение, если вообще будет. Для настоящего ученого вопрос о будущем использовании не возникает, поскольку конечная цель его поведения состоит в формулировке истинного убеждения. Поскольку вероятность прийти к истинному убеждению возрастает по мере увеличения числа фактов, может показаться, будто поиски истины сами себя подрывают, так как ученому, занятому ими, придется собирать доказательства вечно, бесконечно откладывая формирование убеждения. Его затруднения напоминают мучения общества, зацикленного на потреблении, заставляющем его бесконечно экономить и инвестировать, снова и снова откладывая момент наслаждения плодами, ради которых-то и совершались вклады.
На первый взгляд может показаться, что легче определить оптимальное количество фактов в практическом контексте бизнес-решений. Здесь пределы для роста числа фактов возникают, прежде чем мы углубимся в парадоксы максимизации истины, поскольку сбор информации создает издержки для фирмы и потому должен предприниматься только в той степени, в которой имеются (или предполагаются) прибыли. Не получать сведений о среде иррационально, а собирать их слишком долго – тоже; должен иметься некоторый оптимальный объем информации, который будет получен фирмой. Но здесь снова встает вопрос, поскольку «выбор самой максимизирующей прибыль информационной структуры требует информации, и неясно, как максимизатор прибыли, желающий получить информацию, ее приобретает – или гарантирует, что он не переплачивает за нее»[33].
Так звучит общий аргумент для разумной достаточности. Он касается не только решений в бизнесе, но и других практических вопросов, в которых возникает конфликт между стремлением вкладывать время и деньги в получение информации и потребностью тратить их, используя полученную информацию[34]. Это означает, что, когда слабая теория рациональности отброшена, связь между рациональностью и оптимальностью полностью разрывается. Рациональное поведение может описываться в качестве оптимизирующего только – или главным образом – по отношению к данным убеждениям касательно мира, однако принципы рациональности, управляющие получением убеждений, не могут быть объяснены в категориях оптимизации. Аргумент, по крайней мере, выполняется 
Однако выясняется, что эта привлекательная идея, будучи разработана более тщательно, на деле слабее, чем кажется, если только не принять весьма недальнозоркие допущения насчет свойств среды. В любой реалистической модели (например, конкуренции между фирмами) среда, с которой сталкивается фирма, меняется настолько стремительно, что за время, которое потребуется для разгрома конкурентов, любая информационная структура перестанет быть оптимальной. По сути, мы имеем дело с приспособлением к движущейся мишени[35].
Во избежание недоразумений должен добавить, что отношения между правотой и рациональностью несколько сложнее, чем я здесь описал. История науки показывает, что может оказаться рациональным быть неправым и при этом не иррациональным – быть правым. В письме к Мерсенну Декарт пишет, что «скорость и сила камня, выпущенного из пращи, пули, выпущенной из мушкета, или стрелы, выпущенной из арбалета, больше в середине, нежели в начале их полета», предполагая, что это «вульгарное убеждение», но добавляя, что у него имеются основания считать иначе[36].
Ясно, что в 1630 году вульгарное убеждение было рациональным. В случае человека или кареты никто не стал бы спорить, что наивысшая скорость достигается через некоторое время после начала движения, и были все основания распространять это на движение летящего снаряда. Потребовалась гениальность Декарта, чтобы понять движение как состояние, а не процесс[37]. Однако не следует говорить, что убеждение, к которому Декарт пришел, сделав этот поразительный скачок, было иррациональным, поскольку его теория давала возможность воспринять факты, которые ее подтверждали. Вульгарная теория была рациональна ввиду известных ей фактов, теория Декарта – в силу новых фактов, которые она позволила ему установить. Я совершаю банальное утверждение, что отношения между убеждением и наблюдением являются двусторонними, – это не однонаправленный индуктивный процесс, на который указывают словосочетания типа «наиболее рациональное убеждение с учетом имеющихся фактов». Тем самым озарение может являться частью суждения, хоть и необязательной.
Из ранее сказанного мною о неопределенности следует, что в некоторых случаях рационально не формировать никаких убеждений касательно того, какой из возможных исходов осуществится. Позвольте мне напомнить о различии между двумя понятиями убеждения – как суждения о вероятности вообще и как субъективного суждения о ней. Если убеждение в первом смысле понимается в качестве модального оператора, отсюда незамедлительно следует, что нет рациональной потребности формировать убеждение по каждому поводу, поскольку закон исключенного третьего выполняется лишь в отношении пропозиций, а не пропозициональных установок. Если ‘N’ обозначает любой модальный оператор, аналогичный необходимости (убеждение, знание, обязательство и т. д.), тогда ‘p или не-р’ или ‘Np или не-Np’ будут оба истинными, а ‘Np или N(не-р)’ будет ложным. Однако логическая возможность агностицизма не всегда ясно воспринимается, потому что атеизм кажется гораздо более привлекательной альтернативой веры.
Александр Зиновьев предоставил сумасшедшее описание Советского Союза как общества, которое основано на систематическом смешении внутреннего и внешнего отрицания, то есть ‘N(не-p)’ и ‘не-Np’[38]. Смешение ведет к навязчивой тенденции применять закон исключенного третьего к убеждениям и другим модальным операторам, в частности к обязательствам. Например, он сообщает об очень коротком периоде после смерти Сталина, когда было необязательно его цитировать, прежде чем пробел не был закрыт и не стало обязательным не цитировать его в принципе[39].
Все согласны, что применять закон исключенного третьего в подобных случаях – модальная ошибка, однако в сущностной важности этого пункта можно и усомниться. А именно: если убеждение понимается как субъективное суждение о вероятности в рамках модальной интерпретации, соответствующей случаю субъективной уверенности, вполне допустимо утверждать, что всегда можно и всегда нужно формировать некоторые суждения о вероятности того, истинна ли данная пропозиция, даже если нет презумпции того, что речь идет об одном из крайних случаев 0 % или 100 %.
Если же, с другой стороны, принять идею, что настоящее незнание и неопределенность существуют в действительности, тогда попытка сформировать суждение о вероятности может быть довольно иррациональной. Можно определить операционные процедуры, при помощи которых такие вероятности всегда будут получаться при помещении человека в ряд гипотетических ситуаций выбора, однако это малосущественно, поскольку все зависит от того, есть у него какая-то причина доверять вероятностям, полученным таким образом. Опять-таки здесь я не могу подробно излагать мои аргументы в отношении данной точки зрения[40].
Теперь я перейду к сущностной рациональности желаний, куда более запутанному понятию.
Я буду называть ее автономией, являющейся для желания тем, чем суждение является для убеждения. Сложность в описании автономии носит двоякий характер. Во-первых, крайне трудно сказать, что означает в случае желания быть сформированным «должным образом», то есть без искажения не имеющими отношения к делу каузальными процессами.
Во-вторых, может оказаться бесполезно отличать автономию желаний от их добродетельности; во всяком случае, вопреки влиятельнейшей кантианской традиции. Я полагаю, что второе возражение отводится с помощью примеров, в рассмотрении которых у нас возникает желание четко различать гетерономные и неэтичные желания. Однако без хорошего ответа на первое возражение мы остаемся с точностью до второй десятой, при этом не зная, какова первая, ибо как мы можем различать автономное и этическое, если не знаем, что означает автономия?
Я не способен предложить хоть сколько-нибудь удовлетворительное определение автономии. Помимо смутной аналогии с суждением можно себе представить остенсивное определение. Точно так же, как существуют люди, хорошо известные своей способностью суждения, есть люди, которые, по всей видимости, контролируют процессы, при помощи которых формируются их желания, или, по крайней мере, они оказываются неподвластны процессам, с которыми себя не идентифицируют. Однако идентичность и даже само существование этих людей гораздо более спорно, чем в случае способности суждения, что позволяет сделать некоторые оперативные оценки с точки зрения дифференцированного выживания.
С одной стороны, может показаться, будто наш способ выявления подобных индивидов столь тесно связан с нашими этическими воззрениями, что оказывается невозможным провести различие между автономией и добродетелью. С другой стороны, есть опасность, что, когда список неавтономных процессов формирования желания будет расширен, как это уже происходило в прошлом и, несомненно, еще произойдет в будущем, он поглотит все наши желания, не оставив на долю автономии ничего.
Поскольку ранее я метафорически описал иррациональность в категориях «слепой» каузальности, возникает искушение предоставить следующее определение: автономные желания – это желания, которые осознанно выбираются, приобретаются или изменяются либо с помощью акта воли, либо в процессе планирования характера. Таков, например, идеал самоопределения, который лежит в основании философии стоиков, буддистской и спинозистской философии. Далее в главах II и III я более подробно обсуждаю природу и пределы подобного рода управления собой.
Здесь я лишь хочу заметить, что в качестве определения автономии эта идея дает нам одновременно слишком много и слишком мало. Определение слишком слабое, ведь желание, вырастающее из намеренного планирования характера, может быть менее автономным, чем намерение, из которого оно выросло[41], и тогда мы сразу впадаем в регресс. Более того, нет причин полагать, что желания второго порядка всегда надежно защищены от нерелевантных каузальных влияний. Если бы это было так, регресс легко бы пресекался, но, как показано в важной работе Джорджа Эйнсли, желания второго порядка могут принимать навязчивый характер и становиться столь же гетерономными, как и импульсивные желания первого порядка, от которых они были призваны нас защитить[42]. Сама деятельность по планированию характера может привести к его ригидности, которая окажется несовместимой с «терпимостью к двусмысленности», зачастую описываемой как признак прочности эго или автономии. Это определение также слишком сильно: оно лишает желания первого порядка возможности быть рациональными или автономными.
Из убедительного предположения о том, что способность к оценкам второго порядка является условием образования личности, мы не должны делать вывод, что применение этой способности на деле и составляет условие автономий[43]. Благодаря чистому моральному везению[44] люди могут достигать автономии, не стремясь к ней.
В качестве предварительного шага на пути к пониманию автономии, включая вопрос о самой ее возможности, мы можем изучить некоторые из неавтономных способов проявления «я». Данная книга в целом и глава III в частности посвящены прежде всего таким предварительным исследованиям: они предоставят фон, на котором можно было бы выделить широкое понятие о рациональности. Однако даже не зная, что такое автономия, допустимо утверждать, что она отличается от добродетельности. Я приведу несколько аргументов, чтобы показать, что основания, на которых мы критикуем желания за то, что они не автономны, отличаются от тех доводов, на которые мы ссылаемся, когда отвергаем желания как неэтичные, – при этом оставляя открытой возможность того, что неэтичные желания также могут оказаться неавтономными.
Желания или предпочтения могут вызывать возражения либо из-за происхождения (неавтономные желания), либо из-за содержания (неэтичные желания). Ярчайший пример неавтономных предпочтений, обсуждающийся в данной работе, – «кислый виноград», то есть приспосабливание предпочтений к тому, что кажется возможным. Другие важные разновидности – конформизм, то есть адаптация своих предпочтений к предпочтениям других людей, и чистая инерция. Мы также должны включить сюда обратный феномен контрадаптивных предпочтений («С другой стороны забора трава всегда зеленее».), антиконформизм и одержимость новизной. Примеры неэтичных предпочтений несколько более спорны. Чаще всего упоминаются агрессивные и садистские предпочтения, а кроме того, по мнению некоторых, сюда же относится желание иметь «статусные блага», то есть вещи, которые по логике могут иметь лишь немногие[45]. Примером выступает желание иметь доход, который бы в два раза превышал средний. Распространенное желание иметь статусные блага может привести к уменьшению всеобщего благосостояния, поэтому такие предпочтения не выдерживают кантианскую проверку на обобщение[46].
Кроме того, они тесно связаны с озлоблением, поскольку один из способов получить больше остальных – позаботиться о том, чтобы они получили меньше, – в самом деле зачастую более дешев и более эффективен, нежели попытки отличиться в чем-либо[47].
Для того чтобы отличить нехватку автономии от нехватки морального достоинства, я воспользуюсь следующей технической дистинкцией: конформность будет обозначать желание, вызванное стремлением походить на других людей, а конформизм – желание походить на других людей; аналогичным образом будут определяться антиконформность и антиконформизм. (Я коротко вернусь к различию между желаниями и стремлениями, или влечениями.) Конформность предполагает причастность поведения других к каузации моих желаний, а конформизм – неустранимое присутствие их в описании объекта моих желаний[48]. Конформность может порождать конформизм, но она также может приводить к антиконформизму, как в случае замечания Теодора Зелдина, что в среде французских крестьян «престиж достигался, главным образом, за счет конформности традициям (так что от сына нонконформиста ожидали, что он тоже будет нонконформистом)»[49].
Очевидно, что конформность может вызывать желания, которые будут этически приемлемыми, но лишенными автономности. И наоборот, я не вижу способа исключить возможность того, что некто будет автономно иметь антиконформистские предпочтения, хотя приветствовал бы доказательство того, что автономия несовместима не только с антиконформностью, но и с антиконформизмом.
Тем не менее в решении последнего вопроса нет надобности, поскольку первого случая достаточно для объяснения реальности этого различения. Смиренный конформист, чьи действия моральны, потому что его всегда поддерживает среда, которая привила ему правильные желания, едва ли может притязать на автономию. Автономное моральное действие предполагает способность действовать морально даже в неморальной среде. Я не хочу этим сказать, что в подобных случаях следует неизменно выбирать курс действий, который был бы наилучшим, если бы был выбран всеми. Предположительно это не было бы конформистским поведением, однако оно может оказаться неавтономным в каких-либо других аспектах.
Практическая мораль, как правило, имеет дело со «вторым лучшим» выбором[50], что означает: когда другие ведут себя неморально, человек может отклониться от образа не только их действий, но также и поведения, каким бы оно было в идеальной ситуации всеобщей моральности. Слепо действовать в соответствии с каким-то правилом, которое никак не учитывает контекст, не будет признаком автономии. Такое поведение часто встречается у ригидных людей, которые нуждаются в правилах и стремятся избегать применения этического суждения[51]. Хотя подобное поведение может показаться образцом моральности и автономии, на деле оно лишено и того и другого.
В настоящей работе автономность будет пониматься как чистый остаток после вычитания всех желаний, которые были сформированы механизмами, отвечающими за иррациональное формирование предпочтений (я приведу краткий список). Аналогичным образом качество суждения в случае убеждений будет понято как отсутствие искажений и иллюзий. Тем самым намечаются некоторые необходимые условия для рациональности в широком смысле, которые, хотя они куда менее удовлетворительны, чем полное описание, могут, по крайней мере, считаться первым шагом на пути к нему.
Широкая типология механизмов искажения выстраивается, стоит нам заметить, что, подобно ментальным состояниям, которые они порождают, эти механизмы могут быть либо когнитивными, либо аффективными по своему характеру. Конечные состояния могут быть когнитивными или аффективными, то есть описываться как убеждения или как желания. А стало быть, недостаток в них рациональности вызывается либо нарушениями когнитивных процессов, либо пагубным влиянием какого-то аффективного влечения. В сумме мы имеем четыре возможных случая, которые я вкратце опишу на некоторых примерах. Но сначала нужно обосновать разделение между желаниями и влечениями. Влечения формируют желания (и убеждения), но сами желаниями не являются, поскольку они не осознанны, неизвестны испытывающему их человеку. (Поэтому ошибочно говорить вслед за фон Вайцзеккером, что человек, испытывающий навязчивую страсть ко всему новому, имеет «предпочтение новизны»[52].) Влечения также не могут быть уподоблены метажеланиям, которые, хотя они и формируют желания первого порядка, делают это иначе, как я утверждаю далее в главе III.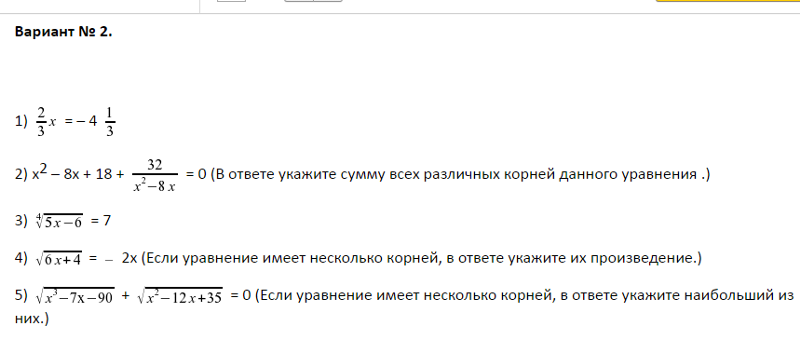
Влечения должны рассматриваться как едва заметные психические силы, нацеленные на поиск краткосрочного удовольствия в отличие от осознанных желаний, которые могут отказываться от краткосрочного удовольствия ради долгосрочного выигрыша[53]. Метафора «сил» призвана подчеркнуть, что мы ничего не знаем о сущностном характере влечений, который при нынешнем состоянии знания и науки приходится выводить из поведения, а не изучать напрямую.
С учетом этого различения мы рассмотрим некоторые случаи, в которых широкая рациональность убеждений и желаний искажается влечениями или когнитивными изъянами. Я не буду расписывать в деталях данные четыре категории, только объясню их на примерах, которые, хотя они и важны, отнюдь не исчерпывают свои классы.
Формирование адаптивных предпочтений – согласование желаний с наличными возможностями – это не намеренная адаптация, к которой стремятся те, кто планирует характер, а каузальный процесс, происходящий неосознанно. Он вызывается влечением к ослаблению напряжения или фрустрации, испытываемым из-за наличия желаний, которые, как кажется, невозможно удовлетворить.
Изменение предпочтений путем переформулирования (framing) происходит, когда относительная привлекательность вариантов меняется из-за другого описания ситуации выбора, хотя с рациональной точки зрения оно не отличается от предыдущего. В недавнем исследовании Амоса Тверски и Даниэля Канемана было показано, что этот эффект носит повсеместный характер в ситуациях выбора и во многом схож с оптическими иллюзиями. Они цитируют пример из Леонарда Сэвиджа с покупателем, который «готов доплатить Х фунтов стерлингов сверх стоимости новой машины, чтобы приобрести модное авторадио, но осознает, что не станет платить Х фунтов за радио по его обычной цене после покупки автомобиля», добавляя, что «многим читателям знакомо временное обесценивание денег, способствующее дополнительным расходам <…> в контексте больших трат, таких как покупка дома или машины». Кроме того, размещая время или деньги, мы, по-видимому, используем внутренний учет, который порой обретает свою собственную власть и заставляет нас менять решение, если расходы переносятся из одной статьи в другую.
Если мы идем покупать билет в театр за пять фунтов и по дороге теряем пятифунтовую банкноту, это нас не остановит, мы все равно его купим, однако если мы его уже купили, а затем потеряли, мы вряд ли захотим купить новый билет[54]. В таких случаях нет никакого влечения, но есть только ригидная когнитивная обработка информации.
Принятие желаемого за действительное – это формирование убеждений под влиянием желаний, заставляющих нас думать, что мир именно таков, каким мы хотим его видеть. Скажем, желание получить повышение по службе может вызвать убежденность в том, что оно вот-вот произойдет. Подобно формированию адаптивных предпочтений, это скорее «горячий», чем «холодный», процесс, но в отличие от него конечным результатом здесь является убеждение, а не желание. Поскольку причины их столь схожи, мы можем ожидать, что эти явления порой будут подменять друг друга, как мы увидим в главах III и IV ниже.
Ошибка в выводе умозаключения – это холодный путь к иррациональным убеждениям.
Разновидности подобных ошибок не так давно были изучены Ричардом Нисбеттом и Ли Россом, которые пришли к выводу, что «интуитивный ученый», то есть каждый из нас в повседневной жизни, склонен совершать удручающе большое число необоснованных суждений и выводов, вызванных недостатками когнитивного аппарата. По своему каузальному механизму такие ошибки напоминают изменения формулировок предпочтений, а по своему эффекту – принятие желаемого за действительное. Типичный пример: «Если индивид с очень большой вероятностью считается республиканцем, но с малой вероятностью считается юристом, он будет с умеренной вероятностью считаться юристом-республиканцем»[55], как если бы вероятности складывались, а не умножались. В данном случае убеждение не является рациональным даже в слабом смысле. Однако во многих других ситуациях страдает прежде всего способность суждения, а не логическая непротиворечивость.
Данный текст является ознакомительным фрагментом.
Double, Float — не вещественные числа / Хабр
Во многих источниках тип double и float, числа с плавающей запятой/точкой зачем-то называют вещественными. Такое чувство что кто-то когда-то совершил ошибку или не внимательно написал эту глупость и все как один начали её повторять, совершенно не задумываясь о чём они говорят.
Ладно это были бы просто троечники студенты и любители, так эту ошибку говорят и те, кто обучают специалистов. И эта проблема терминологии не одного ЯП, их правда много (Java, C++, C#, Python, JS и т.д.) везде, где бы я не искал, всегда находятся статьи, ответы, лекции, где дробные числа называют вещественными!
Вот ОЧЕНЬ МАЛЕНЬКАЯ выборка:
https://javarush.ru/quests/lectures/questsyntaxpro.level04.lecture06 — JavaRush
https://docs-python.ru/tutorial/osnovnye-vstroennye-tipy-python/tip-dannyh-float-veschestvennye-chisla/ — Docs Python3
http://cppstudio.
com/post/310/ — CppStudiohttps://ejudge.ru/study/3sem/sem07.pdf — Ejudge
https://ru.wikipedia.org/wiki/Система_типов_Си — даже всеми любимая Wikipedia!
Ещё раз повторюсь это очень маленькая выборка, можете набрать в гугл поиске, по ключевым словам, и удостовериться что их полно.
com/post/310/ — CppStudioНачнём с простого, что такое вещественное число коим называют double и float. Будет немного формул, но не пугайтесь, прочитайте пожалуйста до конца, они очень простые, к каждой я даю интуитивное объяснение.
Вещественное число
Определение можете прочитать в Википедии или дочитать до конца мою статью, где я простым языком скажу или вы сами поймёте, но нужно проследить за мыслью, которую я хочу донести до вас. Я напишу формулой из теории множеств:
R = Q ∪ I
Где, R — множество вещественных чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел.
Так же Q ⊂ R и I ⊂ R.
Расшифровка тем, кто не очень с теорией множеств.
Вещественные числа эта числа которые включают в себя Рациональные и Иррациональные числа (R = Q ∪ I), т.к. Вещественные числа включают их в себя, то Рациональные числа и Иррациональные числа являются подмножеством множества Вещественных (Q ⊂ R и I ⊂ R), причём строго, то есть Q != R и I != R, это очевидная мысль, но её требуется подчеркнуть.
Теперь к самому интересному, какие числа называются Рациональными и Иррациональными (представляю себя преподавателем начальных курсов технических вузов).
Рациональные
Начнём с Рациональных, возьмём определение из википедии.
Рациональное число (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби m/n, где m — целое число, а n — натуральное.
Так же стоит отметить, что Рациональные включают в себя Целые и Натуральные числа (-1, 0, 1, 2 …) их можно выразить в виде дроби, 1 = 1/1, 2 = 2/1, -1 = -1/1, 0 = 0/1 и т.д.
Почему это важно? Потому что Иррациональные числа не включают в себя Целые и Натуральные числа, это отдельный класс чисел.
Иррациональные
Берём определение из Википедии.
Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби m/n, где m,n — целые числа, n != 0. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Так же приведу примеры иррациональных чисел, чтобы стало понятно: π (число пи), e (число Эйлера), √2.
Вы начали что-то подозревать? Если нет я помогу вам.
Первое предложение определения — это то, о чём я вам говорил, то, что Иррациональные числа — это отдельный класс чисел и он не включает в себя Целые и Натуральные.
Но самое важное здесь это второе предложение «Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.».
Что это значит? Заметили, что в примерах я дал вам буквенное обозначение? Это не просто так, это представление иррационального числа, ВАЖНО — сама запись π это не само иррациональное число, это всего лишь его представление, и оно является чем угодно, но не иррациональным числом.
Само Иррациональное число оно бесконечно. Понимаете?
То есть его невозможно записать по определению. Никакой памяти в компьютере не хватит чтобы его записать. Это невозможно!
И мало того что в большинстве (я не проверял прям на всех, но очень сомневаюсь, что хотя бы в одном это есть) языков в которых используется термин Вещественный тип нельзя чисто синтаксически сделать запись по типу: «double a = π», попросту будет ошибка компиляции, так ещё если и возможно с помощью латинских букв подключая библиотеки, то в конечном-то итоге эта переменная будет ссылаться на конечное представление, а то есть рациональное этого иррационального числа!
Всё с чем мы можем работать это ТОЛЬКО РАЦИОНАЛЬНЫЕ ЧИСЛА, представления иррациональных чисел они ТОЖЕ рациональные и ТОЛЬКО рациональные. Они большие, они могут быть ооооочень большими, но они всё равно рациональные!
R = Q ∪ I, если мы исключаем I из-за невозможности работы с ними в прямом смысле без представлений получается R’ = R\I, R’ = Q, а Q у нас рациональные числа.
Так почему же так много людей и весьма неглупых всё ещё допускают эту простую ошибку? Эту ошибку можно было описать в пару предложений, но я хотел донести до вас последовательно как к этому прийти, используя общепринятую терминологию.
Спасибо.
P.S. Это моя оригинальная статья AfterWing, не является переводом, доработкой другой какой-либо статьи на русском/английском и др. языках.
проверка доказательств — действительный или неверный аргумент — противоречащие аргументы
Задавать вопрос
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 3к раз
$\begingroup$
Мой профессор попросил нас оценить обоснованность следующего аргумента:
Некоторые рациональные числа являются степенями числа 5.
Все целые числа рациональны. Следовательно, некоторые целые числа являются степенями числа 5.Мой профессор снова и снова говорил о справедливости аргумента после того, как я поставил под сомнение его логику. Наконец, он заявил, что аргумент недействителен, и привел такой аргумент:
.Теперь давайте абстрагируемся от этого аргумента, пусть R представляет множество рациональных чисел, P — множество степеней пяти, а G — множество целых чисел. Тогда посылки и заключение становятся: 1) Некоторый элемент R принадлежит P. 2) Все элементы G принадлежат R. Вывод: некоторый элемент из G принадлежит P.
В качестве модели этого аргумента пусть R = {a, b, c}; Р = {с}; и G = {а, Ь}. Верны ли предпосылки? 1) Некоторый элемент R принадлежит P. 2) Все элементы G принадлежат R. Следует ли теперь заключение: какой-то элемент из G принадлежит P?
Я разговаривал с другим профессором, который говорит, что аргумент верен, и я видел разные ответы на эту проблему, включая этот:
Ссылка здесь:
см.
упражнение 6
Вот я и спрашиваю, что правда?
РЕДАКТИРОВАТЬ:
Кроме того, для любого открытого предложения P(x) $$\существует x \in \mathbb{Q} P(x)$$ не эквивалентно, $$\существует x (x \in \mathbb{Q} \Rightarrow P(x))$$ и если они не эквивалентны, то почему автор в приведенном ниже примере перефразирует следующее квантифицированное утверждение как импликацию?
РЕДАКТИРОВАТЬ 2: Этот пост здесь похож на мой последний вопрос.
спасибо.
- доказательство-проверка
- логика
- логика предикатов
$\endgroup$
10
$\begingroup$
Недопустимый аргумент. Вот опровержение по логической аналогии:
Некоторые монеты — десятицентовики
Все пятицентовики — монеты
Следовательно, некоторые пятицентовики — десятицентовики
Аргумент, основанный на формальной логической нотации, неверен, поскольку он использует неправильную символизацию.
Например, некоторые рациональные числа являются степенями пяти и должны быть обозначены как: 9.0003
$$\существует x (Q(x) \land R(x))$$
и не как:
$$\существует x (Q(x) \rightarrow R(x))$$
Итак… либо в тексте предлагалось найти ошибку в «Решении»… либо в тексте было ужасно ошибочное Решение! Учитывая, что все остальное, помеченное как «Решение», кажется, рассматривается как фактический ответ на упражнения, я боюсь, что это последнее … что это за текст?!
$\endgroup$
3
$\begingroup$
Аргумент:
«Некоторые рациональные числа являются степенями 5. Все целые числа рациональны. Следовательно, некоторые целые числа являются степенями 5.»
недопустимо
Рациональные числа, являющиеся степенями числа 5, не обязательно являются целыми числами. Например, $\frac {1}{32}$ — это степень числа 5, но не целое число.
Все целые числа рациональны, но это не означает, что все рациональные числа являются целыми числами.
Если бы все рациональные числа были степенями 5, то мы могли бы утверждать, что все целые числа являются степенями 5, но из того, что некоторые рациональные числа являются степенями 5, мы не можем утверждать, что некоторые целые числа являются степенями 5.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Логика. Какой пример числа, которое не является ни рациональным, ни иррациональным?
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 1к раз
$\begingroup$
Конечно, согласно обычной логике, их нет. Но в интуиционистской логике может быть, как видно из этого ответа: https://math.stackexchange.com/a/1437130/49592.
Мой вопрос, согласно этому ответу, что такое конкретное число, которое не является ни рациональным , ни иррациональным (обратите внимание, что ссылка выше использует другое определение иррационального, чем нормальное).
Также в вопросе вам нужно будет указать, какую модель вы используете.
{-2}$ имеет бесконечно много взаимно простых решений». Проблема заключается в том, что здесь подразумевается под «бесконечно многими». Если это означает, что есть инъекция из $\Bbb N$, то мы получаем тот же набор, который описан другим определением с использованием бесконечных цепных дробей. В частности, если $x$ иррационально, то существует функция $f:\Bbb N\to\Bbb Q$, сходящаяся к $x$, и в лагере «русских конструктивистов» можно считать, что $f$ — вычислимая функция, поэтому $x$ вычислима. И, очевидно, рациональные числа вычислимы.
Таким образом, константа Чайтина $\Omega$ не является ни рациональной, ни иррациональной.
Чтобы было ясно, в конструктивистской логике мы не обязательно знаем, что $\Omega$ существует даже ; на самом деле, в этом вся суть. Но это означает, что мы можем взять марковскую модель конструируемых вещественных чисел $\Bbb R_M$ и добавить $\Omega$, чтобы получить модель $\Bbb R_M[\Omega]=:\Bbb R_{\Omega}$, которая может быть рассматривается как подмножество $\Bbb R$ (в окружающей вселенной, где истинен LEM).