Умножение столбиком многозначных натуральных чисел
Рассмотрим в этой статье как умножать столбиком различные числа — двузначные, трехзначные и другие — большие и маленькие. Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс. Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.
В статье вы рассмотрите подробное решение примеров столбиком на умножение, повторите таблицу умножения и вспомните как решается любой пример на умножение больших чисел. Мы приведем примеры умножения в столбик натуральных чисел.
Содержание
Умножение двузначных чисел столбиком
Умножим два числа: 25 и 44. Когда мы записываем числа столбиком, важно записать их друг под другом так, чтобы десятки были под десятками, единицы под единицами. Вот так считать в столбик:
Правильная запись умножения столбиком
Теперь начинаем последовательно умножать сначала число 25 на первую четверку (число единиц), получим:
Умножение столбиком двузначных чисел 1 часть — умножили число 25 на число единиц (на 4) — получили 100.
Обратите внимание — число 100 записывается в процессе умножения справа налево — то есть, идем от единиц к десяткам, умножаем сначала 5 на 4, получаем 20, записываем 0 под числом единиц, а число 2 держим в уме. Теперь умножаем 2 на 4, получаем 8, но так как у нас в уме еще 2, то складываем 2 и 8, получаем 10, записываем 10, причем так как мы сейчас умножаем число десятков на число единиц второго числа — на 4, то и число 10 записываем, начиная с числа десятков — 0 под десятками и 1 слева. В итоге получаем 100.
В итоге получаем 100.
Мы умножили число 25 на число единиц 4 второго числа 44. Теперь сделаем умножение числа 25 на число десятков 4 числа 44. Результат умножения столбиком начнем писать справа налево, то есть начнем писать его под числом десятков, получим:
Умножение в столбик двухзначных чисел
Итак, мы выполнили умножение числа 25 сначала на число единиц — 4 — второго числа 44, а потом на число десятков — 4 — второго числа 44. Следующим шагом будет сложение этих последовательных результатов умножения. Получим:
Умножение в столбик двузначных чисел результат
Обратите внимание — мы складываем не 100+100, а последовательно числа по разрядам, то есть сначала числа, стоящие на местах единиц (у нас тут один ноль), потом числа стоящие на местах десятков (0+0), числа, стоящие на позиции сотен (1+0) и числа, стоящие на месте тысяч (1). Если число только одно, то мы его просто сносим вниз, мысленно складывая с нулем.
Примеры умножения двузначных чисел
Чтобы лучше разобраться в умножении двузначных чисел столбиком, рассмотрим следующие примеры решения столбиком. Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:
Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:
Пример 1
Умножим число 15 на число 37. Пошаговый алгоритм умножения столбиком:
Умножение двузначных чисел в столбик
Пример 2
Умножим число 23 на число 79. Пошаговый алгоритм умножения столбиком:
Умножение столбиком 23 и 79
Умножение столбиком трехзначных чисел
Для того, чтобы умножать столбиком трехзначные числа — все действия выполняем также, алгоритм не меняется. Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.
Давайте рассмотрим пример умножения столбиком трёхзначного числа на трехзначное число. Пусть нам нужно умножить 345 на 726. Вот что получится — пошаговый алгоритм:
Умножение столбиком трехзначных чисел
Таким образом, общий принцип ясен и можно перемножать в столбик числа с любым количеством знаков.
Умножение столбиком многозначных натуральных чисел
Правильная поразрядная запись умножения столбиком
Теперь рассмотрим, как надо умножать круглые числа. Тут есть небольшая хитрость для удобства умножения.
Тут есть небольшая хитрость для удобства умножения.
Умножение столбиком круглых чисел
Когда мы умножаем в уме круглые числа, мы не обращаем при умножении сначала внимания на ноль, например, нам нужно умножить 50 на 30. Мы в уме перемножаем 5 на 3 и просто приписываем два нуля, памятуя о том, что 10 на 10 дают 100.
Значит, если мы будем умножать, скажем 50 на 35, то эти числа в столбик нам удобнее записать не так:
Запись умножения в столбик круглого числа 1
А так:
Умножение в столбик круглого числа
Тогда нам нужно будет просто умножить число 35 на 5 и приписать 0. Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.
Итак, мы рассмотрели как умножать в столбик двузначные, трехзначные и любые многозначные натуральные числа, рассмотрели алгоритм умножения в столбик, привели примеры такого умножения.
Умножение столбиком многозначных натуральных чисел
Рассмотрим в этой статье как умножать столбиком различные числа — двузначные, трехзначные и другие — большие и маленькие. Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс. Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.
Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс. Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.
В статье вы рассмотрите подробное решение примеров столбиком на умножение, повторите таблицу умножения и вспомните как решается любой пример на умножение больших чисел. Мы приведем примеры умножения в столбик натуральных чисел.
Содержание
Умножение двузначных чисел столбиком
Умножим два числа: 25 и 44. Когда мы записываем числа столбиком, важно записать их друг под другом так, чтобы десятки были под десятками, единицы под единицами. Вот так считать в столбик:
Вот так считать в столбик:
Правильная запись умножения столбиком
Теперь начинаем последовательно умножать сначала число 25 на первую четверку (число единиц), получим:
Умножение столбиком двузначных чисел 1 часть — умножили число 25 на число единиц (на 4) — получили 100.
Обратите внимание — число 100 записывается в процессе умножения справа налево — то есть, идем от единиц к десяткам, умножаем сначала 5 на 4, получаем 20, записываем 0 под числом единиц, а число 2 держим в уме. Теперь умножаем 2 на 4, получаем 8, но так как у нас в уме еще 2, то складываем 2 и 8, получаем 10, записываем 10, причем так как мы сейчас умножаем число десятков на число единиц второго числа — на 4, то и число 10 записываем, начиная с числа десятков — 0 под десятками и 1 слева. В итоге получаем 100.
Мы умножили число 25 на число единиц 4 второго числа 44. Теперь сделаем умножение числа 25 на число десятков 4 числа 44. Результат умножения столбиком начнем писать справа налево, то есть начнем писать его под числом десятков, получим:
Умножение в столбик двухзначных чисел
Итак, мы выполнили умножение числа 25 сначала на число единиц — 4 — второго числа 44, а потом на число десятков — 4 — второго числа 44. Следующим шагом будет сложение этих последовательных результатов умножения. Получим:
Следующим шагом будет сложение этих последовательных результатов умножения. Получим:
Умножение в столбик двузначных чисел результат
Обратите внимание — мы складываем не 100+100, а последовательно числа по разрядам, то есть сначала числа, стоящие на местах единиц (у нас тут один ноль), потом числа стоящие на местах десятков (0+0), числа, стоящие на позиции сотен (1+0) и числа, стоящие на месте тысяч (1). Если число только одно, то мы его просто сносим вниз, мысленно складывая с нулем.
Примеры умножения двузначных чисел
Чтобы лучше разобраться в умножении двузначных чисел столбиком, рассмотрим следующие примеры решения столбиком. Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:
Пример 1
Умножим число 15 на число 37. Пошаговый алгоритм умножения столбиком:
Умножение двузначных чисел в столбик
Пример 2
Умножим число 23 на число 79. Пошаговый алгоритм умножения столбиком:
Умножение столбиком 23 и 79
Умножение столбиком трехзначных чисел
Для того, чтобы умножать столбиком трехзначные числа — все действия выполняем также, алгоритм не меняется.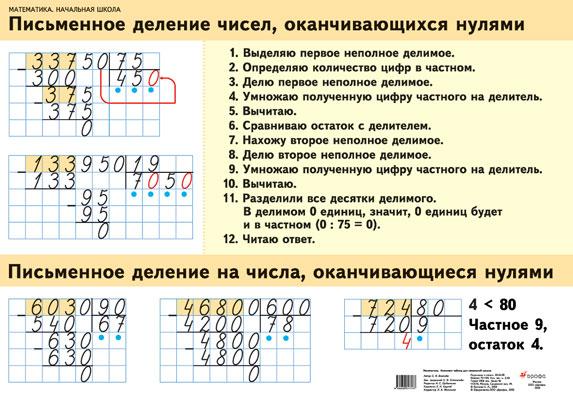 Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.
Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.
Давайте рассмотрим пример умножения столбиком трёхзначного числа на трехзначное число. Пусть нам нужно умножить 345 на 726. Вот что получится — пошаговый алгоритм:
Умножение столбиком трехзначных чисел
Таким образом, общий принцип ясен и можно перемножать в столбик числа с любым количеством знаков.
Умножение столбиком многозначных натуральных чисел
Правильная поразрядная запись умножения столбиком
Теперь рассмотрим, как надо умножать круглые числа. Тут есть небольшая хитрость для удобства умножения.
Умножение столбиком круглых чисел
Когда мы умножаем в уме круглые числа, мы не обращаем при умножении сначала внимания на ноль, например, нам нужно умножить 50 на 30. Мы в уме перемножаем 5 на 3 и просто приписываем два нуля, памятуя о том, что 10 на 10 дают 100.
Значит, если мы будем умножать, скажем 50 на 35, то эти числа в столбик нам удобнее записать не так:
Запись умножения в столбик круглого числа 1
А так:
Умножение в столбик круглого числа
Тогда нам нужно будет просто умножить число 35 на 5 и приписать 0. Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.
Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.
Итак, мы рассмотрели как умножать в столбик двузначные, трехзначные и любые многозначные натуральные числа, рассмотрели алгоритм умножения в столбик, привели примеры такого умножения.
Как умножать многозначные числа, используя метод ящика и развернутую форму (без перегруппировки или переноса) — цените знания выше оценок
Хотите, чтобы был более простой способ умножения?
Умножение многозначных чисел традиционным способом может оказаться немного сложным по нескольким причинам. Один потому, что при переноске приходится переключаться с умножения на сложение, что я всегда забывал делать в школе, а иногда и до сих пор делаю. Кроме того, со всеми этими пробелами, которые вы создаете внизу после каждого шага, трудно сказать, почему метод, который вы используете, действительно работает.
В этой статье и видео я буду учить 5 примеров Коробочного метода умножения с использованием расширенной формы каждого числа, что поможет нам выполнять одну операцию за раз: умножать, затем складывать. И я буду использовать свой любимый метод для добавления «Значение в обратном порядке».
Метод Box также облегчает нагрузку, так что мы, по сути, выполняем однозначное умножение и просто записываем нули после этих произведений, когда это уместно.
Когда вы почувствуете, что освоили Box Method, попробуйте его самостоятельно, загрузив Практический лист с 3 вопросами из KOG Math Success Library с вашей бесплатной учетной записью.
Временные метки видео:
1:03 — Правила умножения методом Box
2:30 — 1 на 2 цифры Пример: 75 x 5
6:38 — 1 на 3 цифры Пример: 379 x 2
9: 29 — 2 по 2 цифры Пример: 12 x 71
11:53 — 2 по 3 цифры Пример: 871 x 52
18:15 — 3 по 3 цифры Пример: 646 x 712
Правила игры
Нарисуйте сгруппированные прямоугольники со столбцами, соответствующими цифрам первого числа, и строками, соответствующими цифрам второго числа.

Запишите первое число в развернутом виде сверху, а второе сбоку, поместив каждое значение над квадратиком.
Умножьте каждое верхнее число на каждое боковое число, вписав произведение в клеточку, где они встречаются.
Сложите все продукты вместе.
Словарь: Понимание математического языка
Цифра: одна из цифр от 0 до 9
Размеры [напр. x-цифры на y-цифры]: единиц измерения, которые представляют длину, ширину, высоту и т. д., которые могут иметь единицы измерения в дюймах, футах, милях, метрах и т. д. В нашем случае размеры нашего сгруппированного поля диаграммы представляют собой длину и ширину в единицах «количества цифр в числе»
Place Value: значение цифры в числе, основанное на ее позиции и степени, кратной степени 10 (см. таблицу разрядности и примеры здесь).
Произведение: результат перемножения чисел
Коммутативное свойство умножения: В слово коммутативный входит слово «commute», что означает передвигаться или путешествовать. Следовательно, это определение означает, что при умножении числа можно перемещать или переупорядочивать, и все равно получается один и тот же продукт.
Следовательно, это определение означает, что при умножении числа можно перемещать или переупорядочивать, и все равно получается один и тот же продукт.
Почему используется коммутативное свойство?
При рисовании диаграмм сгруппированных блоков применяется то же правило.
Например, если у нас есть 17 x 439, будет работать как блочная диаграмма 2 на 3, так и блочная диаграмма 3 на 2. Его можно нарисовать любым способом:
Коммутативное свойство умножения позволяет нам умножать не по порядку, что позволяет нам рисовать наш метод ящика по-разному и получать один и тот же ответ.
Начнем умножать!
Пример 1:
75 x 5 (1 цифра на 2 цифры)Нажмите, чтобы посмотреть этот пример.
Я нарисовал сгруппированную диаграмму 1 на 2 цифры, которая отражает 5 x 75, и она будет такой же, если мы нарисуем диаграмму с группировкой 2 на 1, которая будет отражать 75 x 5.

Учитывая количество строк и столбцов, 5 имеет 1 цифру, которая соответствует количеству строк (1), а 75 имеет 2 цифры, которые соответствуют количеству столбцов (2). Число 75 было расширено до 70 + 5, и каждое значение места было написано над столбцом.
Я умножил каждое разрядное значение 75 (есть 2) на каждое разрядное значение 5 (есть 1).
70 x 5 = 350
5 x 5 = 25
Наконец, я сложил все продукты вместе, используя метод Backwards Place Value, чтобы не было перегруппировки или переноса.
350 + 25 = 375
Мой ответ: 375 🙂
Вы можете посмотреть, как я преподаю этот пример в моем видеоуроке, нажав ЗДЕСЬ.
Пример 2:
2 x 379 (1 цифра на 3 цифры) Нажмите, чтобы посмотреть этот пример.
Я нарисовал сгруппированную диаграмму 3 на 1 цифру, которая отражает 379 x 2. Это получится так же, если мы нарисуем диаграмму с группировкой 1 на 3 цифры, которая будет отражать 2 x 379
Учитывая количество строк и столбцов, 379 имеет 3 цифры, которые соответствуют количеству строк (3), а 2 имеет 1 цифру, которая соответствует количеству столбцов (1).
Число 2 содержит только 1 разрядное значение (единицы), поэтому нет необходимости расширять его.
Число 379 содержит 3 разряда, поэтому оно было расширено до 300 + 70 + 9, и каждое разрядное значение было записано над столбцом.
Я умножил каждое разрядное значение 379 (есть 3) на каждое разрядное значение 2 (есть 1).
300 х 2 = 600
9x 2 = 18
Наконец, я сложил все продукты вместе, используя метод обратного размещения значений, чтобы не было перегруппировки или переноса.

И мой ответ 758 🙂
Вы можете посмотреть, как я преподаю этот пример в моем видеоуроке, нажав ЗДЕСЬ.
Пример 3: 1
2 x 71 (2 цифры по 2 цифры)Нажмите, чтобы посмотреть этот пример.
Я нарисовал диаграмму с группировкой 2 цифры на 2 цифры, которая отражает либо 1 2 x 71 , либо 71 x 12 , поскольку оба числа являются двузначными.
Учитывая количество строк и столбцов, 12 имеет 2 цифры, соответствующие количеству строк (2), а 71 имеет 2 цифры, соответствующие количеству столбцов (2).
Я умножил каждое разрядное значение 12 (их 2) на каждое разрядное значение 71 (их 2).
70 x 10 = 700
70 x 2 = 140
1 x 10 = 10
1 x 2 = 2
Последний используя метод обратного размещения стоимости, чтобы не было перегруппировки или переноса.

И 852 мой ответ 🙂
Вы можете посмотреть, как я преподаю этот пример в моем видеоуроке, нажав ЗДЕСЬ.
Пример 4:
52 x 871 (2 цифры по 3 цифры)Нажмите, чтобы посмотреть этот пример.
Я нарисовал сгруппированную диаграмму 2 на 3 цифры, которая отражает 52 x 871
Число 52 содержит 2 разряда, поэтому оно было расширено до 50 + 2, и каждое разрядное значение было записано рядом с каждой строкой.
Число 871 содержит 3 разряда, поэтому оно было расширено до 800 + 70 + 1, и каждое разрядное значение было записано над столбцом.

Я умножил каждое разрядное значение 52 (всего 2) на каждое разрядное значение 871 (всего 3).
50 х 800 = 40 000
50 х 70 = 3 500
50 x 1 = 50
2 x 800 = 1 600
2 x 70 = 140
2 x 1 = 2
. используя метод обратного размещения стоимости, чтобы не было перегруппировки или переноса.
40 000 + 3500 + 1 600 + 140 + 50 + 2 = 45 292
и 45,292 — мой ответ 🙂
Вы можете посмотреть, как я преподаю этот пример в моем видео, нажимая здесь.
Пример 5: 646
x 712 (3 цифры по 3 цифры)Нажмите, чтобы посмотреть этот пример.
Я нарисовал сгруппированную диаграмму 3 на 3 цифры, которая отражает либо 646 x 712 , либо 712 x 646 , поскольку оба числа являются трехзначными.

Учитывая количество строк и столбцов, 712 имеет 3 цифры, соответствующие количеству строк (3), а 646 имеет 3 цифры, соответствующие количеству столбцов (3).
Я умножил каждое разрядное значение 712 (всего 3) на каждое разрядное значение 646 (всего 3).
700 x 600 = 42 000
700 x 40 = 28 000
700 x 6 = 4,200
10 x 600 = 600059
- 9004 70044 4. 4. 40536
4 10. 9000 9000 9000
4 10. 9000 9000
4 10.
.- . х 6 = 60
2 х 600 = 1200
2 х 40 = 80
2 х 6 = 12
Наконец, я сложил все продукты вместе, используя метод обратного размещения стоимости, чтобы не было перегруппировки или переноса.
42 000 + 28 000 + 4 200 + 6000 + 1200 + 40 + 60 + 80 + 12 = 459 952
и 459 952 — мой ответ 🙂 учебник, нажав ЗДЕСЬ.
Прокомментируйте и дайте мне знать ниже…
Что вы думаете о методе умножения ящиков и сложении с помощью метода обратного разряда значений? Видите, никакой перегруппировки или переноски, верно? Воспользуетесь ли вы им в следующий раз, когда вам нужно будет умножать? Как вы думаете, это занимает слишком много времени? Дайте мне знать.
ХОТИТЕ ЭТО ПОПРАКТИЧЕСКИ?
Skill Builder
Каждое из моих учебных видео снабжено Skill Builder для дополнительной практики. Они поставляются с практическими листами и викториной, которую вы можете пройти столько раз, сколько вам нужно, чтобы получить высший балл. Если вам интересно, нажмите на ссылку, чтобы узнать больше.
Мне нужно потренироваться
2-значное умножение — шаги
LearnPracticeDownload
2-значное умножение или двузначное умножение выполняется путем упорядочивания чисел таким образом, что заданные числа располагаются одно под другим. Двузначное число можно умножить на однозначное, на другое двузначное число, на трехзначное число и так далее. Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
Двузначное число можно умножить на однозначное, на другое двузначное число, на трехзначное число и так далее. Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Что такое двузначное умножение? |
| 2. | 2-значное умножение на 2-значное |
| 3. | 2-значное умножение с перегруппировкой |
| 4. | Часто задаваемые вопросы по двузначному умножению |
Что такое двузначное умножение?
Двузначное умножение — это метод умножения двузначных чисел, занимающих два разряда, т. е. единиц и десятков. Способ умножения чисел такой же, как и умножения однозначных цифр. Однако в двузначных числах мы умножаем каждую цифру по одной на множитель. Это означает, что множитель сначала умножается на разряд единиц множимого, а затем на разряд десятков множимого.
Умножение 2-значных чисел на 1-значное
Умножение 2-значных чисел на 1-значные очень просто. Давайте разберемся в этом, используя следующие шаги и пример.
Пример: Умножить 23 × 2
- Шаг 1: Поместите однозначное число под двузначным. Это делает однозначное число множителем. Умножьте однозначное число (множитель) на единицу множимого. Здесь 2 — это множитель, а единица множимого равна 3. Таким образом, 2 × 3 = 6. Это частичное произведение (6) будет помещено под колонку единиц.
- Шаг 2: Теперь умножьте множитель на разряд десятков множимого. Здесь 2 — это множитель, а цифра десятков множимого равна 2. Это означает, что 2 × 2 = 4. Это частичное произведение (4) будет помещено в столбец десятков. Следовательно, 23 × 2 = 46 .
Теперь давайте научимся умножать двузначные числа на двузначные числа.
2-значное умножение на 2-значное
Умножение 2 цифр на 2 цифры означает, что оба числа, которые нужно умножить, состоят из двух цифр. Умножение начинается с разряда единиц, а затем переходит к разряду десятков. Цифры располагаются одна под другой. Хотя любое из двух чисел можно поместить сверху или снизу, предпочтительнее поместить меньшее число снизу, потому что это облегчает умножение. Давайте разберемся с этим умножением с помощью следующего примера. Умножим 34 × 12. В этом случае пусть 34 будет множимым, а 12 — множителем.
- Шаг 1: Поместите множимое (34) сверху, а множитель (12) под ним, как показано на рисунке выше. Умножьте цифру единиц множителя на множимое. Здесь 34 — множимое, а цифра единиц 12 — 2. Это даст 34 × 2 = 68. Это первое частичное произведение, которое будет помещено в одну строку.
- Шаг 2: Умножьте множимое на разряд десятков множителя. Здесь 34 — это множимое, а цифра десятков множителя равна 1.
 Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение. продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.
Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение. продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь. - Шаг 3: Добавьте оба частичных продукта, чтобы получить конечный продукт. Это будет 68 + 340 = 408.
Теперь давайте узнаем о двузначном умножении, в котором у нас есть переносы.
2-значное умножение с перегруппировкой
Двузначное умножение с перегруппировкой или переносом происходит при переносе числа вперед. Давайте поймем это на следующем примере и шагах. Умножим 45 × 6,
- Шаг 1: Умножьте множитель на единицу множимого. Здесь множимое равно 45, цифра единиц в числе 45 равна 5, а множитель равен 6. Таким образом, это будет 6 × 5 = 30.
- Шаг 2: Поскольку произведение, полученное на шаге 1, равно 30, мы перенесем 3 в предыдущий столбец десятков и запишем 0 под столбцом единиц как частичное произведение.

- Шаг 3: Теперь мы умножим множитель на разряд десятков множимого. Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0036
Двузначное умножение с десятичными дробями очень похоже на обычное умножение с использованием нескольких правил десятичных чисел. Давайте узнаем больше об этом в следующем разделе.
Двузначное умножение с десятичными дробями
Двузначное умножение с десятичными дробями выполняется так же, как и обычное умножение двузначных цифр с учетом правил десятичных чисел. При умножении таких чисел мы можем игнорировать десятичную точку, пока не получим окончательный результат. После получения окончательного результата подсчитываем количество знаков после запятой в обоих числах, складываем их и в соответствии с этим ставим запятую. Разберем это на примере и умножим 2,5 × 1,1
Разберем это на примере и умножим 2,5 × 1,1
- Шаг 1: Расположите числа вертикально в соответствии со значением разряда. Не выравнивайте числа по десятичной точке.
- Шаг 2: Умножьте единицу множителя на множимое. Здесь 25 × 1 = 25, .
- Шаг 3: Поместите ноль под цифрой единиц частичного произведения.
- Шаг 4: Умножьте разряд десятков множителя на множимое. Это будет 25. Поместите это рядом с 0 под частичным произведением.
- Шаг 5: Добавьте два продукта, чтобы получить конечный продукт. Здесь 25 + 250 = 275, .
- Шаг 6: Поместите десятичную точку через 2 знака справа в конечном продукте. Поскольку множимое и множитель имеют по 1 десятичному знаку, получается 1 + 1 = 2 десятичных знака. Поэтому ставим запятую через 2 знака справа и получаем 2,5 × 1,1 = 2,75
☛ Связанные темы
- Вычитание 2 цифр
- 2-значное дополнение
- Трехзначное дополнение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Умножение и деление целых чисел
Примеры двузначного умножения
Пример 1: Найдите произведение 67 × 20.

Решение: Давайте разберемся с этим двузначным умножением, используя следующие шаги.
- Умножить 0 на 7 и 6.
- Поместите ноль под цифрой единиц частичного произведения.
- Умножить 2 на 7 и 6.
- Добавьте продукты, чтобы получить окончательный ответ.
Следовательно, 67 × 20 = 1340.
Пример 2: Умножить 31 × 7
Решение: Выполним это двузначное умножение, используя следующие шаги.
- Умножить 7 на 1, то есть 7 × 1 = 7
- Теперь умножьте 7 на 3, то есть 7 × 3 = 21
- Запишите их вместе как 217
- Следовательно, 31 × 7 = 217
Пример 3: Укажите истинное или ложное значение умножения 2-значного числа.
а.) 10 × 11 = 110
б.) 20 × 20 = 40
Решение:
а.) Верно, 10 × 11 = 110
б.) Ложь, 20 × 20 = 400
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению двузначных чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о двузначном умножении
Что такое двузначное умножение?
Двузначное умножение — это метод умножения двузначного числа на другое число. Числа располагаются друг под другом для выполнения умножения. Число, написанное сверху, называется множимым, а число, написанное ниже, — множителем. Двузначные числа можно умножать на однозначные числа, двузначные числа и так далее.
Как выполнить двузначное умножение?
Следующие шаги объясняют процесс двузначного умножения. Например, давайте умножим 42 × 3
- Расположите числа одно под другим так, чтобы большее число (42) было сверху, а меньшее (3) — под ним. Итак, 3 становится множителем, а 42 — множимым.

- Начните умножать множитель с разряда единиц множимого. Здесь 3 будет умножено на 2, что даст 3 × 2 = 6. Это 6 будет записано как частичное произведение.
- Затем умножьте 3 на разряд десятков множимого, то есть 4, что будет 3 × 4 = 12. Теперь, записав оба произведения вместе, конечный продукт будет 42 × 3 = 126
Как выполнить двузначное умножение с переносом?
Двузначное умножение с переносом выполняется, когда произведение одного столбца больше 9. Лишняя цифра переносится в следующий столбец и прибавляется к этому конкретному произведению. Например, давайте умножим 45 × 7.
- Поместите 45 сверху и 7 под ним, чтобы 45 стало множимым, а 5 стало множителем.
- Умножьте 7 на 5, и вы получите 7 × 5 = 35. Поскольку произведение представляет собой двузначное число 35, мы перенесем 3 в столбец десятков и запишем 5 под столбцом единиц как частичное произведение.
- Теперь умножьте множитель на разряд десятков множимого.
 Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Как умножить 2-значное на 1-значное?
Умножение двух цифр на одну цифру выполняется так же, как умножение одной цифры. Например, умножим 13 × 2,9.0005
- Двузначное число (13) записывается сверху, а однозначное (2) — снизу, поэтому 13 становится множимым, а 2 — множителем.
- Начинаем умножать младшую цифру (множитель) на единицу множимого. Здесь мы умножим 2 на 3, что будет 2 × 3 = 6. Мы запишем это 6.
- Затем мы идем дальше и умножаем нижнюю цифру (множитель) на разряд десятков множимого. Здесь 2 × 1 = 2. Это также будет записано вместе с произведением, полученным на предыдущем шаге. Итак, это даст произведение 13 × 2 = 26,9.0036
Как выполнить двузначное умножение на двузначное?
Умножение двух цифр на две цифры — это процесс умножения, при котором двузначное число умножается на другое двузначное число. Например, давайте умножим 23 × 14.
Например, давайте умножим 23 × 14.
- Поместите 23 сверху и 14 под ним, чтобы 23 стало множимым, а 14 стало множителем.
- Умножьте разряд единиц множителя на множимое. Здесь 23 — множимое, а цифра единиц 14 — 4. После умножения 23 на 4 мы получаем 23 × 4 = 9.2. Это первый неполный товар, который будет размещен в одной строке.
- Умножьте множимое на разряд десятков множителя. Это означает, что мы умножим 23 на 1, и это будет 23 × 1 = 23. Следует отметить, что нам нужно поставить ноль под цифрой единиц частичного произведения, а затем написать второе частичное произведение рядом с ним. (Этот 0 помещен здесь, потому что мы фактически умножаем 23 на 10 на этом шаге.) Таким образом, мы получаем здесь 230.
- Теперь мы добавим оба частичных произведения, чтобы получить конечный продукт. это будет 92 + 230 = 322.
- Следовательно, конечный продукт равен 23 × 14 = 322.
Как умножить 3-значное на 2-значное?
Умножение 3-значного на 2-значное означает, что мы умножаем 3-значное число на 2-значное число.





 Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение. продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.
Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение. продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.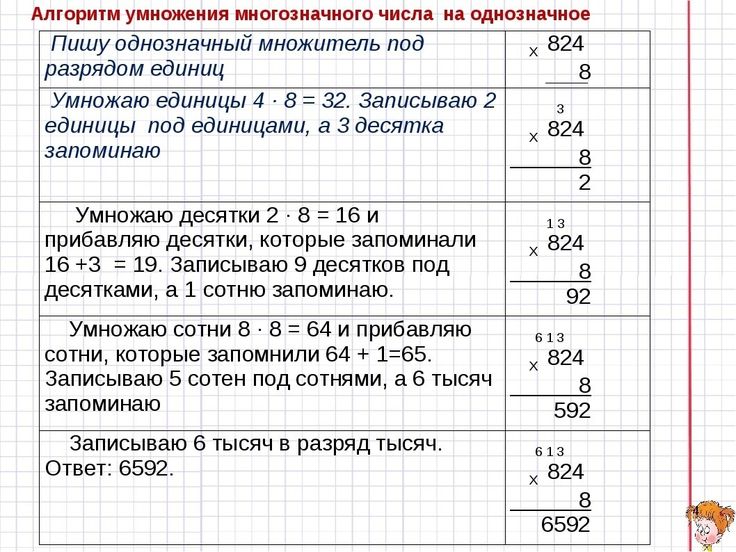

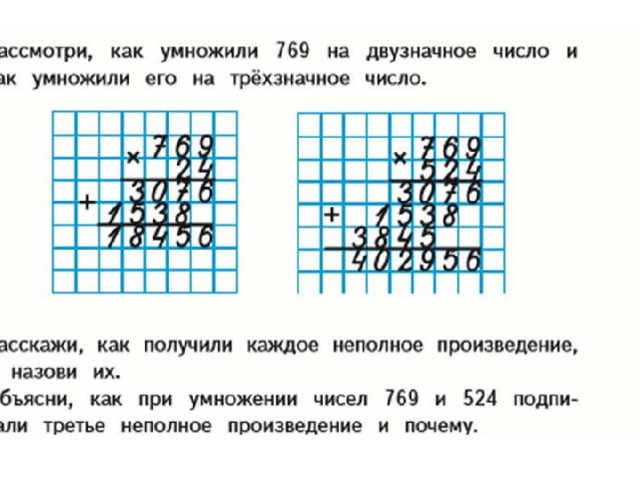
 Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.