Правила знаков при умножении и делении: 1) Сформулируйте правила знаков при умножении и при делении 2) а)-32:8= б)-54:(-6)= в)42:(-7)= г)0:(-3)=

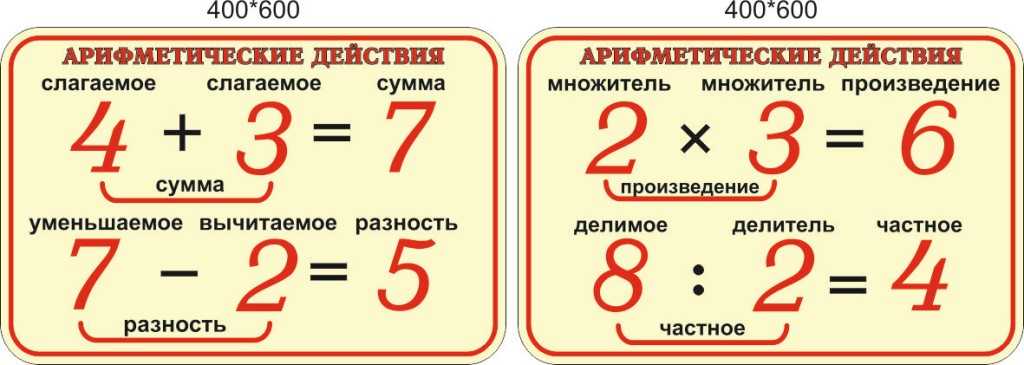
Деление 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Деление на положительное число эквивалентно умножению на обратное ему число. Например,  или .

 

Но у любого отрицательного числа тоже есть обратное. И деление на отрицательное число тоже можно заменить умножением на обратное:  или .

Давайте вспомним определение. Два числа называются взаимно обратными, если их произведение равное единице: если , то  и  – взаимно обратные числа.

Но это значит, что взаимно обратные числа всегда имеют один и тот же знак. Если бы они были разных знаков, то их произведение получилось бы отрицательным.

 

Правила деления

 

 

Отрицательное число можно представить как произведение  на противоположное положительное число: . Этот факт и позволяет получить правила умножения чисел с разными знаками. Например:  Но при делении получается такая же ситуация: 

 

То есть правило деления чисел с разными знаками аналогично правилу умножения. Их даже можно объединить в одно правило: выполнять умножение или деление двух чисел нужно, не обращая внимания на знаки. Если числа были одного знака, то результат будет положительным, а если разного – то отрицательным.

 

Примеры

 

 

1) .

 

Делим, не обращая внимания на знак. Так как числа разных знаков, то в ответе ставим минус: .

2) .

Делим  на , так как числа оба отрицательные, то ответ положительный: .

3) 

Делим  на , так как знаки у чисел разные, в ответе минус: .

Часто, чтобы понять, какой знак получится, правило запоминают так: «минус на минус дает плюс, плюс на минус дает минус». Это верно и для умножения и для деления.

4) 

Делимое и делитель можно умножить на . Так как числа разных знаков, то в ответе ставим минус: .

5) .

Знак ответа минус, его можно сразу поставить впереди, т.к. у чисел разные знаки. Деление заменяем умножением. Сокращаем и получаем ответ: .

6) .

Сразу определяем знак. Минус на минус дают плюс. Запишем смешанную дробь в виде неправильной и сократим на , деление на  означает умножение на . Выделяем целую часть и получаем ответ: .

7) .

Дробь – это тоже деление. Минус на минус дают плюс. Сокращаем дробь на  и на . Можно записать в виде десятичной дроби: .

8) .

Если в выражении несколько операций умножения и деления, то правило то же самое. Два первых минуса дают плюс. Остается один. В ответе минус. Или так: всего три минуса. Нечетное количество минусов дает минус: .

 

Заключение

 

 

Деление можно считать умножением. Поэтому правило умножения чисел с разными знаками подходит и для деления. Заключается правило в следующем: чтобы выполнить действия с несколькими умножениями и делениями, нужно выполнить действия, не обращая внимания на знаки. Четное количество минусов в исходном выражении даст плюс в ответе, нечетное – минус.

 

Если мы умножаем всего два числа или делим одно число на другое, то правило звучит проще: минус на минус дает плюс, плюс на минус дает минус.

Тот факт, что деление можно заменить умножением на обратное число, мы использовали, чтобы объяснить, почему правило умножения подходит и для деления.

При расчетах такую замену делать совсем не обязательно. Все зависит от конкретного примера. В примере  это в самом деле удобно сделать: . А в примере , если заменить деление умножением, то удобнее не станет, поэтому считаем так, как есть: .

 

Список рекомендованной литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
2. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. М. «Просвещение», 2010.
3. Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Yaklass.ru (Источник).
2. Math-prosto.ru (Источник).
3. Mathematics-repetition.com (Источник).

 

Домашнее задание

• Определите знак частного:

а) ;

б) ;

в) .

• Выполните деление: .

Найдите значение выражения:

 

Вся элементарная математика — Средняя математическая интернет-школа

Действия с отрицательными и положительными числами

Абсолютная величина (модуль). Сложение.

Вычитание. Умножение.  Деление.

Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на  « + »;  для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.

П р и м е р ы : | – 5 | = 5,    | 7 | = 7,    | 0 | = 0.

Сложение :

1) при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак. П р и м е р ы : ( + 6 ) + ( + 5 ) = 11 ; ( – 6 ) + ( – 5 ) = – 11 . 2) при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной. П р и м е р ы : ( – 6 ) + ( + 9 ) = 3 ; ( – 6 ) + ( + 3 ) = – 3 .

Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.

П р и м е р ы :

( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;

( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;

( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;

( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;

Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак  « + » , если знаки сомножителей одинаковы, и знак  « – » , если знаки сомножителей разные.

Полезна следующая схема ( правила знаков при умножении ):

+ · +   =   +

+ · –   =   –

– · +   =   –

– · –   =   +

При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.

П р и м е р :

Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.

Здесь действуют те же правила знаков, что и при умножении :

+ : +   =   +

+ : –   =   –

– : +   =   –

– : –   =   +

П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .

Назад

Правило знаков — Math28

Содержание

Определение положительного или отрицательного знака

Знаки, сопровождающие числа, очень важны, так как они указывают, положительное это число или отрицательное.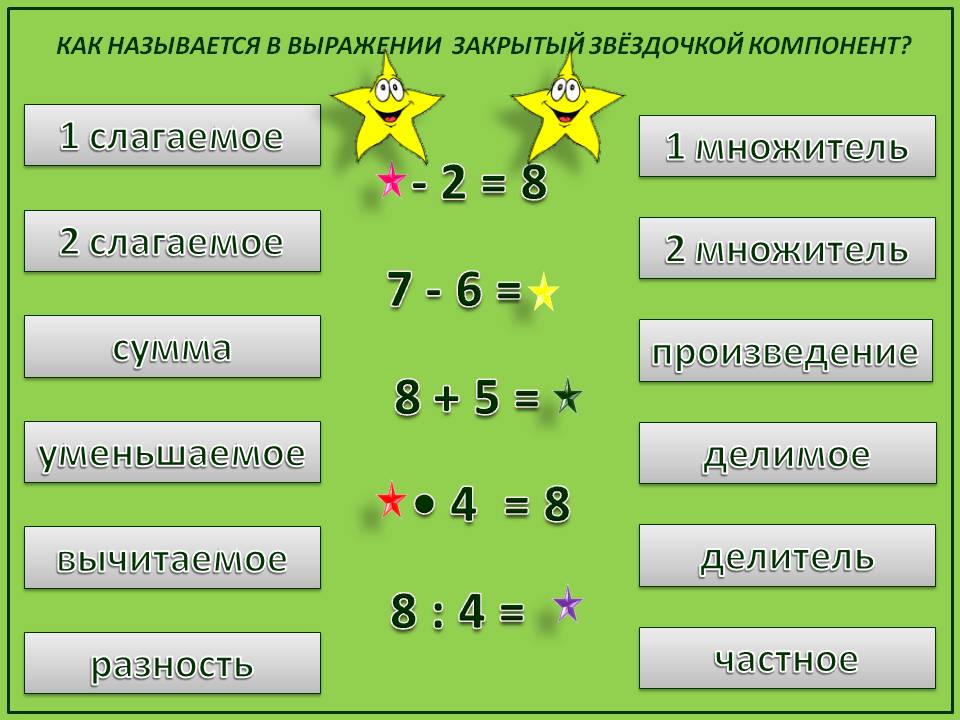

Чтобы определить, является ли число положительным, слева от числа ставится крест, хотя во многих случаях знак не ставится, и считается, что оно положительное, с другой стороны, чтобы определить, является ли число отрицательным, средний тире или черта ставится слева от числа.

3 ← Положительный
+ 3 ← Положительный
— 3 ← Отрицательный

Примечание : Для положительного числа слева от числа у нас нет другого числа, которое можно оставить без знака.

В числовой строке вы можете увидеть разницу между числом с положительным знаком и числом с отрицательным знаком.

• -1
• 0
• 1

Ноль считается нейтральным числом, слева от нуля предыдущей строки соответствуют отрицательные числа до самой бесконечности (-inf), а справа от нуля положительные числа до самой бесконечности (+inf). обдуманный

---

Законы или правила знаков

Закон или правило знаков указывает на знак, преобладающий при выполнении операций двух одинаковых или разных знаков, и применяется по-разному для различных математических операций:

Правило знаков для сложения и вычитания

• При сложении двух положительных чисел результат будет иметь положительный знак. 3 + 5 = 8
• При сложении или вычитании двух чисел, одно с положительным знаком, а другое с отрицательным знаком, результат будет иметь знак наибольшего числа. 5 — 6 = — 1
• При сложении или вычитании двух чисел, одно с отрицательным знаком, а другое с положительным знаком, результат будет иметь знак наибольшего числа. — 7 + 4 = — 3
• При вычитании двух отрицательных чисел результат будет иметь отрицательный знак. — 5 — 4 = — 9

Упрощение вышеизложенного:

положительный y положительный = положительный
положительный + отрицательное = наибольшее число
отрицательное + положительное = наибольшее число
отрицательное y отрицательное = отрицательное

Узнать больше о: « Сумма » →

Узнать больше о: « Вычитание » →

Правило знаков для умножения и деления

• При умножении или делении двух положительных чисел результат будет иметь положительный знак. (+) х (+) = +
  (+) ÷ (+) = +
• При умножении или делении двух чисел, одно с положительным знаком, а другое с отрицательным знаком, результат будет иметь отрицательный знак. (+) х (-) = —
  (+) ÷ (-) = —
• При умножении или делении двух чисел, одно с отрицательным знаком, а другое с положительным знаком, результат будет иметь отрицательный знак.
  (-) х (+) = —
  (-) ÷ (+) = —
• При умножении или делении двух отрицательных чисел результат будет иметь положительный знак. (-) х (-) = +
  (-) ÷ (-) = +

Узнать больше о: « Умножение » →

Узнать больше о: « Подразделение » →

Правило знаков для потенцирования

• Если показатель степени равен даже , результатом будет знак положительный . (+) ^пар = +
  (-) ^пар = +
• Если показатель степени равен , нечетное , результат сохранит знак основного числа. (+) ^импар = +
  (-) ^импар = —

Узнать больше о: «Экспонент

» →

Основные правила для положительных и отрицательных чисел

• ОПИСАНИЕ

  правила сложения и вычитания двух положительных и отрицательных чисел

• ИСТОЧНИК

  Attribution-Non Derivatives 4.0 International (CC BY-ND 4.0) / Создано Beth Wiggins для YourDictionary

• PERMISSION

  кроме нуля являются отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.

  При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.

  Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.

  Реклама

  Дополнение: одинаковые знаки, добавьте числа

  Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:

  • 1 + 1 = 2
  • 51 + 32 = 83
  • -14 + (-6) = -20
  • -196 + (-71) = -267

  Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.

  Сложение: разные знаки, вычитание чисел

  Реклама

  Если вы складываете вместе положительные и отрицательные числа, вычтите меньшее число из большего и используйте знак из большего числа. Например:

  • 6 + (-5) = 1
  • -17 + 22 = 5
  • -100 + 54 = -45
  • 299 + (-1) = 298

  Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.

  Вычитание: Переключиться на сложение

  Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:

  • -3 — (+5) становится -3 + (-5) = -8
  • 9 — (-7) становится 9 + (+7) = 16
  • -14 — (+8) становится -14 + (-8) = -22
  • 25 — (-90) становится 25 + (+90) = 115

  Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно делайте их положительными. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.

  Реклама

  Умножение и деление: один и тот же знак, положительный результат

  Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:

  • 8 x 4 = 32
  • (-8) x (-4) = 32
  • 10 x 9 = 90
  • (-10) x (-9) = 90

  То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:

  • 12 ÷ 6 = 2
  • -12 ÷ (-6) = 2
  • 100 ÷ 5 = 20
  • -100 ÷ (-5) = 20

  числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.

  • Описание

    Правила для умножения и деления двух чисел положительных и отрицательных

  • Источник

    Атрибутив-не Деривативы 4.0 Международный (CC BY-ND 4.0) / Создано Beth Wiggins для вашего Dydictionary

  • Регламент

    Принадлежит YourDictionary, Copyright YourDictionary

  Умножение и деление: противоположный знак, отрицательный результат

  Реклама

  При умножении положительного на отрицательное произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:

  • 6 х (-7) = -42
  • -7 х 6 = -42
  • 12 х (-11) = -132
  • — 11 x 12 = -132

  Во всех этих случаях сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
  

  Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки подряд. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:

  • 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
  • 9 + (-8) = 1 (+- не похожи на знаки, поэтому уравнение представляет собой вычитание)
  • 11 — (+13) = 2 (-+ разные знаки, поэтому уравнение представляет собой вычитание)
  • 15 — (-10) = 25 (— подобны знакам, поэтому уравнение представляет собой сложение)

  Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать с знаки заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.