Состав Числа Примеры Тренировки Хитрости в Мышлении
Для чего нужно знать состав числа?
Как упражнения по составу чисел могут помочь вашему ребенку , Какая польза от знания состава числа.
Ответы на эти вопросы Вы можете получить у нас на сайте.
С составом числом знакомиться уже начинают в детском саду, в старших группах есть занятия по подготовке детей к школе. Малышей учат считать и решать простенькие примеры и задачи.
А для этого детям дают задание запомнить состав числа.
В возрасте 6-7 лет ребенка знакомят с составом чисел от 0 до 10 . Изучение состава числа поможет будущему школьнику легко освоить сложение и вычитание.
К этому возрасту ребенок знает наизусть прямой счет до 10, обратный счет в пределах 10, умеет пересчитывать и отсчитывать предметы, знает состав числа из единиц: понимает, что 3 — это 1 и 1 и 1. Все это говорит о том, что ваш ребенок готов к изучению состава чисел до 10 из двух меньших чисел.
Состав числа начинают изучать с опорой на наглядный материал.
Когда мы просто складываем разные числа, результат может получиться любой. Но когда мы выясняем состав какого-то числа, то как бы идём в обратном направлении — от результата, который известен заранее. Мы учим определённые пары слагаемых — у каждого числа они свои, — чтобы получался именно этот результат.
Помните
Знание состава числа — залог быстрого счета, устного и письменного. Если во время подготовки к школе состав числа до 10 не уложился у ребенка в голове, надо обязательно уделить этому время в первом классе, а потом не забывать о закреплении состава числа до 20 и далее — это сильно сократит время на вычисления.
Я предлагаю действовать в таком порядке.
- Объяснить наглядно, как при одной и той же сумме одно слагаемое может увеличиваться, а второе — уменьшаться. Очень удобно это делать на предметах, которых всегда фиксированное и привычное глазу количество: отлично подходят коробки из-под яиц (10), прозрачные упаковки печенья или конфет (обычно 6, 8, 12), строчки календаря (7), упаковки акварели, пластилина и т.п.
- Ребёнок обязательно должен записать в тетрадь (или на листочек) все возможные варианты состава числа, проговорить их вслух, найти и соединить примеры с одинаковыми слагаемыми (7+1 и 1+7, например) если он конечно может писать.

- Очень советую сделать для закрепления состава числа карточки вида
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
Отдельную карточку на каждый пример. Зачем? Карточки составом числа дают нам много возможностей для заучивания комбинаций.
Обзаведитесь карточками на состав числа. Их можно купить или сделать. Они бывают нескольких типов, и лучше, чтобы они были двух видов. Разрезная карточка состоит из двух половинок. На одной изображён 1 предмет, на другой — 1, 2, 3 и больше точно таких же предметов. Половинки могут быть соединены знаком «+», но «плюс» можно сделать и отдельно. Второй комплект представляет собой набор картинок, на которых изображены эти же предметы одним множеством, без всякого разделения. Когда ребёнок хорошо научится сопоставлять число и цифру, можно сделать такие же карточки с цифрами. Их может быть несколько комплектов, чтобы представлять каждое число в разных вариантах.
Проводите занятия регулярно. Покажите ребёнку карточку, на которой изображено, скажем, 5 предметов.
Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.
Аналогичные задания поводите и с цифрами. Покажите, например, число 9 и точно так же, как в предыдущем случае, предложите найти несколько вариантов его состава. Объясните ребёнку, что чем больше число — тем больше возможностей его составить.
Например:
- Раскладываем карточки по порядку.
- Просим ребёнка все их назвать.
- Переворачиваем, кладём карточки лицевой стороной вниз.
- Просим ребёнка их припомнить.
- Открываем, проверяем, хвалим!
Сделать столько раз, сколько понадобится, чтобы ребёнок назвал их все. Заниматься можно буквально по нескольку минут, между делом.
Поговорим о хитростях запоминания
Расскажите, что любое число всегда состоит из единицы и предыдущего числа. Таким образом, если нужно определить состав числа 8, у ребенка уже готов один ответ: 8 – это 1 и 7. Соответственно, чтобы определить, сколько будет 8 минус 1, нужно от 8 отчитать 1 в обратном порядке, то есть назвать предыдущее число.
Таким образом, если нужно определить состав числа 8, у ребенка уже готов один ответ: 8 – это 1 и 7. Соответственно, чтобы определить, сколько будет 8 минус 1, нужно от 8 отчитать 1 в обратном порядке, то есть назвать предыдущее число.
Познакомьте ребенка также с отсчетом 2. Чтобы ответить на вопрос: 8 – это 2 и сколько?, нужно сначала отсчитать 1 в обратном порядке, а потом еще 1.
Больше практикиЧтобы довести определение состава числа до автоматизма, решайте как можно больше примеров. Можно играть в игру: вы называете число, состав которого нужно определить, ребенок как можно быстрее показывает любое уместное количество пальцев, вы показываете оставшееся количество. Потом меняетесь ролями. Эта игра также тренирует навык сравнения, ведь если вы назовете 4, ребенку нельзя показать 5 и более пальцев.
Это интересно, читайте также:
Изучаем Состав Числа в виде Игры
Тренировка
А теперь будем тренировать запоминание. Точнее, припоминание. Теперь наши задания направлены на то, чтобы ребёнок припоминал нужные примеры.
Точнее, припоминание. Теперь наши задания направлены на то, чтобы ребёнок припоминал нужные примеры.
Задание 1. Я делаю так — даю листок с примерами, где есть и те примеры, которые мы сейчас учим, и другие. Инструкция для ребёнка: «Найди все примеры, которые мы сейчас учили, и запиши правильный ответ. На другие примеры сейчас не обращай внимания».
(Некоторые прилежные дети начинают всё равно решать все примеры. Поэтому я стараюсь подбирать такие «ненужные» примеры, которые они должны были уже освоить.)
Самое главное — наблюдать за ребёнком в процесс работы: он припоминает примеры (те, которые мы сейчас заучиваем) или заново считает? Если считает — ничего не получилось! Либо ребёнок их ещё не запомнил (тогда надо вернуться к пункту 3), либо не понимает, чего мы сейчас от него хотим. Нам нужно именно это: найти знакомые примеры!
Задание надо выполнить хотя бы 3- раза (не сразу, с интервалами, в один день не более двух раз через промежуток времени).
Задание 2. Снова даём ребёнку листок с примерами, где есть и те, которые мы «учили», и на состав других чисел. И просто просим решать примеры. Не подсказываем, что некоторые примеры он уже «помнит».
Наблюдаем. Делаем выводы: если вспоминает «наши» примеры и сразу пишет в них ответы — ура, получилось! Если нет — возвращаемся к пункту 3.
Примеры с вычитанием
Теперь нас ждёт непростой момент — мы должны научить ребёнка решать примеры на вычитание, используя знание состава числа.
Если мы помогаем первокласснику, необходимо использовать математические термины: «Когда мы складываем два слагаемых, у нас получается сумма. Это примеры на сложение. А что такое пример на вычитание? Это когда мы знаем сумму и знаем одно слагаемое, а второе слагаемое не знаем. Как его найти? Для этого из суммы мы вычитаем известное слагаемое.
Но если ты помнишь состав числа, то неизвестное слагаемое ты можешь просто припомнить. Мы с тобой выучили состав числа 8. Ты помнишь все комбинации? Перечисли!»
Ты помнишь все комбинации? Перечисли!»
Ребёнок отвечает:
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4 + 4 = 8
«Молодец! А теперь давай будем менять числа местами! Наши примеры будут на вычитание, поэтому сумму 8 мы всегда будем ставить на первое место. Вычитать можно только из самого большого числа! Вычитать будем одно из слагаемых, а второе будет получаться в ответе. Давай попробуем: называй любой пример на сложение с ответом 8!»
5 + 3 = 8
«Сейчас мы с тобой будем „прятать“ одно слагаемое, делать его неизвестным. Что у нас получится:
8 — 5 = ?
Правильно, 3! Второе слагаемое!
Давай попробуем ещё раз:
6 + 2 = 8
А сколько будет:
8 — 6 = ?
Правильно, 2 — второе слагаемое!».
На этом этапе я даю детям вот такие примеры:
6 + 2 =
2 + 6 =
8 — 2 =
8 — 6 =
5 + 3 =
3 + 5 =
8 — 3 =
8 — 5 =
Такая последовательность примеров помогает ребёнку осознать связь сложения и вычитания. И опять же — всё направлено на запоминание. Когда мы решаем примеры на вычитание, можно посчитать, а можно припомнить. Припоминать — быстрее!
Когда мы решаем примеры на вычитание, можно посчитать, а можно припомнить. Припоминать — быстрее!
Момент связи сложения и вычитания очень важен для решения уравнений. Если ребёнок не улавливает эту связь, ему будет трудно решать уравнения.
Заполни пустые места или запоминанием состав числа
Скажем, 5 это 1 плюс 4, или 2 плюс 3, или 3 плюс 2, или 4 плюс 1.
Малыши заучивают это как стишок или скороговорку, зачастую просто не вникая или не понимая смысла.
Для того, чтобы состав чисел от 1 до 10 действительно отложился в детских головках, Ментальная Арифметика предлагает скачать карточки-задания на состав числа.
Для того, чтобы заполнить пустые места надо подумать. Раздумья ускоряют память детей и соответственно мысль.
Желаем Вам успехов в познании математических цифр.
Авторская статья от Аллы Ромашкиной
Ваш сайт Ментальная Арифметика.
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Состав числа
Примеры на время (состав 10) | Тренажёр по математике (1 класс):
3 + 7 = 10 – 2 = 2 + 8 = 10 – 4 = 7 + 3 = 8 + 2 = 5 + 5 =
10 – 2 = 1 + 9 = 10 – 0 = 10 + 0 = 10 – 1 = 3 + 7 = 10 – 2 =
2 + 8 = 10 – 5 = 8 + 2 = 10 – 5 = 5 + 5 = 10 – 1 = 1 + 9 =
10 – 3 = 3 + 7 = 10 – 1 = 1 + 9 = 10 – 5 = 8 + 2 = 10 – 4 =
7 + 3 = 10 – 1 = 5 + 5 = 10 – 3 = 8 + 2 = 10 – 6 = 3 + 7 =
10 – 2 = 2 + 8 = 10 – 2 = 7 + 3 = 10 – 0= 6 + 4 = 10 – 7 =
4 + 6 = 10 – 2 = 2 + 8 = 10 – 8 = 6 + 4 = 10 – 5 = 8 + 2 =
10 – 0 = 5 + 5 = 10 – 3 = 4 + 6 = 10 – 1 = 9 + 1 = 10 – 2 =
8 + 2 = 10 – 0 = 0 + 10 = 10 – 4 = 1 + 9 = 10 – 7 = 9 + 1 =
10 – 1 = 1 + 9 = 10 – 7 = 7 + 3 = 10 – 3 = 7 + 3 = 10 – 4 =
9 + 1 = 10 – 2 = 1 + 9 = 10 – 9 = 3 + 7 = 10 – 2 = 2 + 8 =
10 – 5 = 9 + 1 = 10 – 1 = 4 + 6 = 10 – 5 = 8 + 2 = 10 – 5 =
0 + 10 = 10 – 5 = 8 + 2 = 10 – 2 = 8 + 2 = 10 – 1 = 6 + 4 =
10 – 4 = 2 + 8 = 10 – 9 = 5 + 5 = 10 – 7 = 0 + 10 = 10 – 1 =
7 + 3 = 10 – 1 = 7 + 3 = 10 – 8 = 6 + 4 = 10 – 4 = 5 + 5 =
10 – 6 = 4 + 6 = 10 – 4 = 2 + 8 = 10 – 0 = 7 + 3 = 10 – 6 =
1 + 9 = 10 – 2 = 1 + 9 = 10 – 3 = 1 + 9 = 10 – 5 = 2 + 8 =
10 – 0 = 2 + 8 = 10 – 2 = 8 + 2 = 10 – 2 = 4 + 6 = 10 – 3 =
6 + 4 = 10 – 7 = 6 + 4 = 10 – 5 = 3 + 7 = 10 – 4 = 8 + 2 =
10 – 1 = 3 + 7 = 10 – 2 = 6 + 4 = 10 – 6 = 7 + 3 = 10 – 0 =
6 + 4 = 10 – 3 = 0 + 10 = 10 – 5 = 7 + 3 = 10 – 5 = 5 + 5 =
10 – 9 = 9 + 1 = 10 – 7 = 1 + 9 = 10 – 4 = 4 + 6 = 10 – 1 =
0 + 10 = 10 – 4 = 1 + 9 = 10 – 2 = 4 + 6 = 10 – 5 = 3 + 7 =
10 – 0 = 5 + 5 = 10 – 0 = 10 + 0 = 10 – 1 = 0 + 10 = 10 – 3 =
1 + 9 = 10 – 6 = 0 + 10 = 10 – 3 = 6 + 4 = 10 – 2 = 9 + 1 =
10 – 4 = 7 + 3 = 10 – 8 = 4 + 6 = 10 – 5 = 8 + 2 = 10 – 0 =
5 + 5 = 8 + 2 = 4 + 6 = 10 – 3 = 3 + 7 = 10 – 2 = 6 + 4 =
Примеры композиции функций — Math Insight
Композиция функций — это комбинация двух функций для формирования новой функции. Просто берут выходные данные первой функции и используют их в качестве входных данных для второй функции. Этот процесс работает до тех пор, пока вторая функция будет принимать выходные данные первой функции в качестве своих входных данных (т. е. домен второй функции должен содержать диапазон первой функции). Композицию можно проиллюстрировать, используя метафору функциональной машины, соединяя функциональные машины вместе.
Просто берут выходные данные первой функции и используют их в качестве входных данных для второй функции. Этот процесс работает до тех пор, пока вторая функция будет принимать выходные данные первой функции в качестве своих входных данных (т. е. домен второй функции должен содержать диапазон первой функции). Композицию можно проиллюстрировать, используя метафору функциональной машины, соединяя функциональные машины вместе.
Здесь мы демонстрируем процесс составления функций на ряде примеров.
Пример 1: Функция бабушки
Функция матери $m$ — это функция, которая принимает человека $x$ в качестве входных данных и выводит мать этого человека $m(x)$. Мы можем сформировать бабушкину функцию $g$, скомпоновав материнскую функцию с самой собой. Применение этой комбинированной функции к человеку $x$ выведет мать матери человека $x$, которую мы могли бы обозначить как $g(x) = m(m(x))$. Функция бабушки хорошо определена, потому что диапазон функции матери $m$ — это множество женщин, у которых были дети, и это множество является подмножеством домена функции матери, то есть множества всех людей.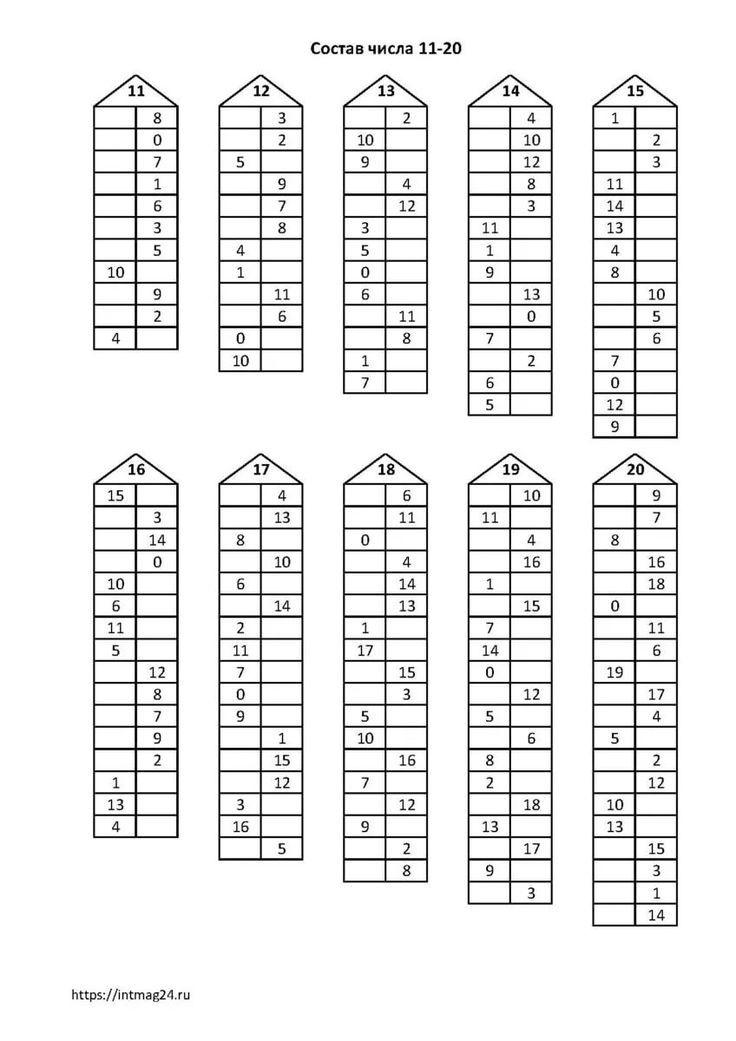 2}.$$ 92}$. Композиция $f \circ m$ не будет работать, потому что $m$ выводит людей, а $f$ ожидает на входе действительное число. Если вы подумаете о метафоре функциональной машины, люди, выходящие из функциональной машины $m$, застрянут во входной воронке функциональной машины $f$. Точно так же композиция $m \circ f$ не сработает, так как материнская функция $m$ не будет знать, что делать с числами, которые выводит $f$.
2}.$$ 92}$. Композиция $f \circ m$ не будет работать, потому что $m$ выводит людей, а $f$ ожидает на входе действительное число. Если вы подумаете о метафоре функциональной машины, люди, выходящие из функциональной машины $m$, застрянут во входной воронке функциональной машины $f$. Точно так же композиция $m \circ f$ не сработает, так как материнская функция $m$ не будет знать, что делать с числами, которые выводит $f$.
Пример 5
Пусть $f$ — функция $f: \R_{\ge 0} \to \R$, где область определения $\R_{\ge 0}$ — множество неотрицательных действительных чисел , $\R_{\ge 0} = \{x \in \R : x \ge 0\}$. Можем ли мы определить композицию $f \circ g$, где $g$ — функция $g: \R \to \R$? Домен $f$ — это неотрицательные действительные числа, но домен $g$ — это целая вещественная строка. Не зная диапазона $g$, мы не можем исключить возможность того, что $g$ может выводить отрицательное число.
Если бы $g(x)$ могло быть отрицательным числом для некоторого входа $x$, то $f$ не знала бы, что делать с входом $g(x)$, и композиция $f \circ g $ не будет определен. 3+1}$ не определяется этим определением $g$. Чтобы сделать эту композицию четко определенной, нам пришлось бы изменить домен $g$ (например, исключить входные данные меньше -1), чтобы убедиться, что она никогда не выводит отрицательное число. 92+1}$ для всех действительных входов $x$.
3+1}$ не определяется этим определением $g$. Чтобы сделать эту композицию четко определенной, нам пришлось бы изменить домен $g$ (например, исключить входные данные меньше -1), чтобы убедиться, что она никогда не выводит отрицательное число. 92+1}$ для всех действительных входов $x$.
Составные функции – объяснение и примеры
В математике функция – это правило, которое связывает данный набор входных данных с набором возможных выходных данных. Важно отметить, что каждый вход связан ровно с одним выходом.
Процесс именования функций известен как нотация функций. Наиболее часто используемые обозначения функций включают: «f(x) = …», «g(x) = …», «h(x) = …» и т. д.
В этой статье мы узнаем что такое составные функции и как их решать.
Что такое составная функция?
Если нам даны две функции, мы можем создать другую функцию, вставив одну функцию в другую. Шаги, необходимые для выполнения этой операции, аналогичны тому, когда любая функция решается для любого заданного значения. Такие функции называются составными функциями.
Такие функции называются составными функциями.
Составная функция — это обычно функция, написанная внутри другой функции. Композиция функции осуществляется путем замены одной функции на другую функцию.
Например, , f [g (x)] является составной функцией f (x) и g (x). Составная функция f [g (x)] читается как «f of g of x ». Функция g(x) называется внутренней функцией, а функция f(x) — внешней функцией. Следовательно, мы можем также прочитать f[g(x)] как «функция g является внутренней функцией внешней функции f ».
Как решать составные функции?
Решение сложной функции означает нахождение композиции двух функций. Мы используем маленький кружок (∘) для обозначения функции. Вот шаги по решению составной функции:
- Перепишите композицию в другой форме.
Например,
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x² ) = f [g (x²)]
- Замените переменную x во внешней функции на внутреннюю.

- Упрощение функции.
Примечание: Порядок в композиции функции важен, потому что (f ∘ g) (x) НЕ совпадает с (g ∘ f) (x).
9Пример 1 (Икс).Решение
Подставим x на 2x – 1 в функции f(x) = x 2 + 6.
(f ∘ g) (x) = (2x – 1) 2 + 6 = ( 2x – 1) (2x – 1) + 6
Применение ФОЛЬГИ
= 4x 2 – 4x + 1 + 6
= 4x 2 – 4x + 7
Пример 2
Учитывая функции g (x) = 2x – 1 и f (x) = x
Решение
Подставить x на x 2 + 6 в функции g (x) = 2x – 1
(g ∘ f) (x) = 2(x 2 2 + 6) – 1
= 2x 2 + 12 – 1
= 2x 2 + 11
Пример 3
Учитывая f (x) = 2x + 3, найти (f ∘ f) (x).
Решение
(F ∘ F) (x) = F [F (x)]
= 2 (2x + 3) + 3
= 4x +
Пример 4
Найдите (g ∘ f) (x), учитывая, что f (x) = 2x + 3 и g (x) = –x 2 + 5
⟹ (g ∘ f) (x) = g [f (x )]. 5
5
= –4x 2 – 12x – 9 + 5
= –4x 2 – 12x – 4
+ 4 и g (x) = x – 3
Решение
Сначала найдите значение f(g(x)).
⟹ f (g (x)) = 5(x – 3) + 4
= 5x – 15 + 4
= 5x – 11
Теперь подставим x в f(g(x)) на 6
⟹ 5(6) – 11
⟹ 30 – 11
= 19
Следовательно, f [g (6)] = 19
Пример 6
Найдите f [g (5)], учитывая, что f (x) = 4x + 3 и g (x) = x – 2. значение f[g(x)].
⟹ f(x) = 4x + 3
⟹ g(x) = x – 2
f[g(x)] = 4(x – 2) + 3
= 4x – 8 + 3
= 4x – 5
Теперь оцените f [g (5)], заменив x в f[g(x)] на 5.
f [g (x)] = 4(5) – 5
= 15
Следовательно, f [g (5)] = 15,9Пример 7 ) = f [g(x)]
Замените x в f(x) = 8x² на (2x + 8)
⟹ (f ∘g) (x) = f [g(x)] = 8(2x + 8) ²
⟹ 8 [4x² + 8² + 2(2x) (8)]
⟹ 8 [4x² + 64 + 32x]
⟹ 32x² + 512 + 256 x
x 0 03 + 1 256 32x²
Пример 8
Найти (g ∘ f) (x), если f(x) = 6 x² и g(x) = 14x + 4
Решение
⟹ (g ∘ f) (x) = g [f(x)]
Подставить x в g(x) = 14x + 4 с 6 x²
⟹g [f(x)] =14 (6 x²) + 4
= 84 x² + 4
Пример 9
Рассчитайте (f ∘ g) (x), используя f(x) = 2x + 3 и g(x) = — x 2 + 1,
Решение
(f ∘ g) (x) = f(g(x))
= 2 (g(x)) + 3
= 2(-x 2 + 1) + 3
= – 2 x 2 + 5
Пример 10
Учитывая f(x) = √ (x + 2) и g(x) = ln (1 – x 2 ), найдите область определения (g ∘ f) (x).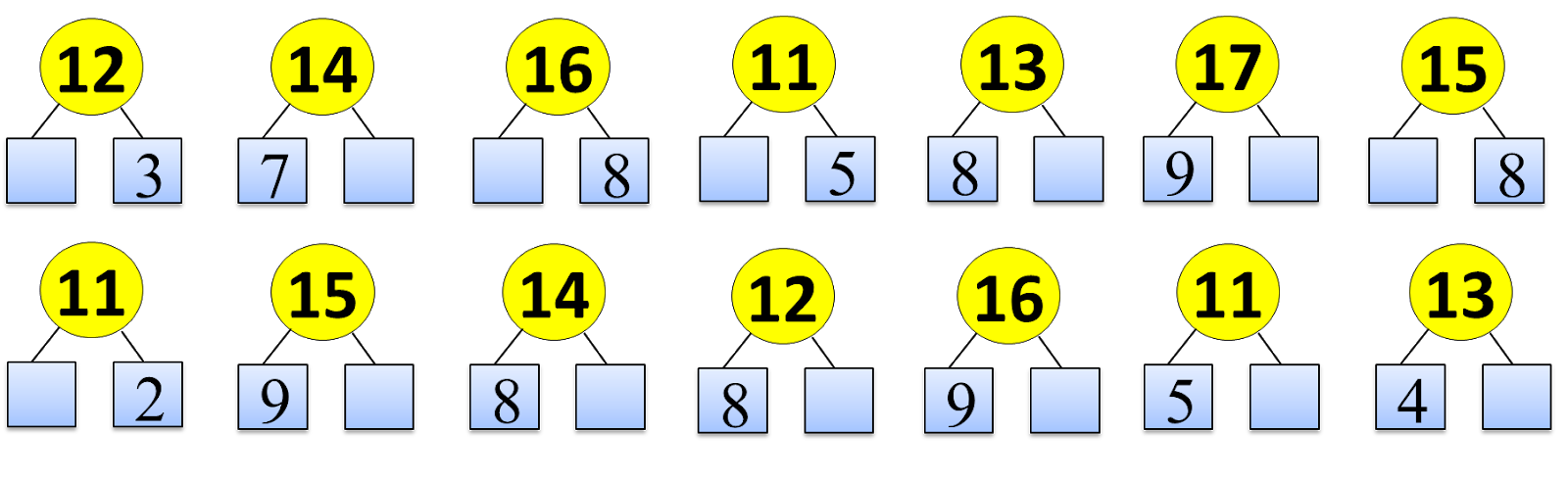

 Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.
Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребёнок тоже даёт вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.