деление и умножение смешанных дробей
Вы искали деление и умножение смешанных дробей? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как дробь умножить на дробь с разными знаменателями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «деление и умножение смешанных дробей».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как деление и умножение смешанных дробей,как дробь умножить на дробь с разными знаменателями,как дробь умножить на другую дробь,как перемножать дроби с разными знаменателями,как перемножить дроби с разными знаменателями,как решать дроби с разными знаменателями на умножение и деление,как умножать дроби неправильные,как умножать дроби с разными знаменателями,как умножать дроби с разными знаменателями и целыми числами,как умножать дроби с разными знаменателями и числителями,как умножать дроби с целыми числами и разными знаменателями,как умножать и делить дроби с разными знаменателями и числителями,как умножать смешанные числа с разными знаменателями,как умножаются дроби с разными знаменателями,как умножить две дроби с разными знаменателями,как умножить дроби с разными знаменателями,как умножить дроби с разными знаменателями и целыми числами,как умножить дроби с разными знаменателями и числителями,как умножить дробь на дробь с разными знаменателями,как умножить дробь на дробь с разными знаменателями и числителями,как умножить дробь на неправильную дробь,как умножить неправильную дробь на дробь,перемножение дробей с разными знаменателями,правило умножения дробей с разными знаменателями,при умножении дробей с разными знаменателями,произведение дробей с разными знаменателями,смешанную дробь умножить натуральное число на дробь,сокращение дробей умножение дробей,умножение дробей с неизвестными,умножение дробей с разным знаменателем,умножение дробей с разными,умножение дробей с разными знаменателями,умножение дробей с разными знаменателями примеры с решением,умножение дробей с разными знаменателями с целыми числами,умножение дробей с целыми числами и разными знаменателями,умножение и деление дробей с разными знаменателями умножение и деление,умножение и деление смешанных дробей,умножение неправильных дробей,умножение с дробей,умножение смешанных дробей,умножение смешанных дробей с разными знаменателями,умножения дробей с разными знаменателями,умножить дроби.
Решить задачу деление и умножение смешанных дробей вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор дробей онлайн
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей.
Вид дроби: простые дроби смешанные дроби
| Дробь 1 | Дробь 2 | |||||||||
| +−×÷ | = | |||||||||
| +/− | +/− |
Вычислить
Решение:
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется
Пример:
2
= 2 +
=
+
=
Похожие калькуляторы
Сравнения дробей Сокращения дробей Возведение дроби в степень
операций над дробями | Математика для гуманитарных наук Необходимый предмет
Результаты обучения
- Сложение или вычитание дробей.
- Упростить дроби.
- Умножение дробей.
- Разделить дроби.
Студенты-математики и работающие взрослые часто обнаруживают, что их знания о том, как складывать, вычитать, умножать и делить дроби, заржавели от неиспользования. Мы склонны полагаться на калькуляторы, которые делают за нас большую часть работы с дробями. Тем не менее, студенческая алгебра создает некоторые важные методы работы с выражениями и уравнениями, основанные на операциях над дробями. Поэтому важно заново освоить эти навыки. Этот раздел напомнит вам, как выполнять действия над дробями. По мере прохождения оставшейся части курса вы можете возвращаться к этому разделу по мере необходимости для быстрого напоминания об операциях с дробями.
Прежде чем мы начнем, давайте определимся с терминологией.
- произведение: результат умножения
- фактор: что-то умножается — для [латекс]3 \cdot 2 = 6[/латекс] , и [латекс]3[/латекс] и [латекс]2[/латекс] являются множителями [латекс]6[ /латекс]
- числитель: верхняя часть дроби – числитель дроби [латекс]\крупный\фрак{2}{3}[/латекс] равен [латекс]2[/латекс]
- знаменатель: нижняя часть дроби — знаменатель дроби [латекс]\большой\фракция{2}{3}[/латекс] равен [латекс]3[/латекс]
Примечание об инструкциях
Определенные слова используются в учебниках по математике и учителями, чтобы предоставить учащимся инструкции о том, что делать с данной задачей.
Например, вы можете увидеть такие инструкции, как найти или упростить. Важно понимать, что означают эти слова, чтобы успешно решать задачи этого курса. Вот краткий список некоторых инструкций по решению проблем вместе с их описаниями, поскольку они будут использоваться в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполнить указанные математические операции, которые могут включать сложение, вычитание, умножение, деление (позже использование слова найти будет расширено до решения уравнений, как в найти значение переменной). |
| Упростить | 1) Выполнять указанные математические действия, включая сложение, вычитание, умножение, деление 2) Напишите математическую формулировку в наименьших выражениях, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценка | 1) Выполнять указанные математические действия, включая сложение, вычитание, умножение, деление 2) Подставить заданное значение переменной в выражение и затем выполнить указанные математические операции |
| Уменьшить | Напишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением |
Сложение дробей
Когда вам нужно складывать или вычитать дроби, сначала нужно убедиться, что дроби имеют одинаковый знаменатель.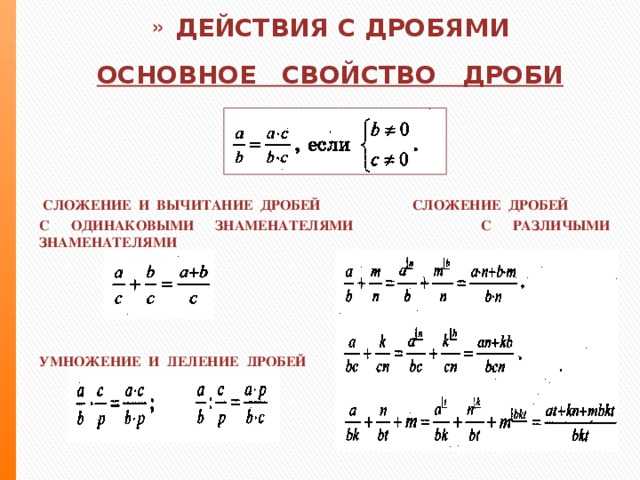
Концепция «части целого» может быть смоделирована с помощью пиццы и кусочков пиццы. Например, представьте, что пицца разрезана на [латекс]4[/латекс] куска, и кто-то берет [латекс]1[/латекс] кусок. Теперь [latex]\Large\frac{1}{4}[/latex] из пиццы исчезает, а [latex]\Large\frac{3}{4}[/latex] остается. Обратите внимание, что обе эти дроби имеют знаменатель [латекс]4[/латекс], который относится к количеству ломтиков, на которые была разрезана вся пицца. Что, если у вас есть еще одна пицца, разрезанная на [латекс]8[/латекс] равных частей, и [латекс]3[/латекс] из этих частей исчезли, оставив [латекс]\большой\фрак{5}{8} [/латекс]?
Как можно описать общее количество оставшейся пиццы одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, если число кратно другому, вы можете разделить их и не получить остатка.
Один из способов найти наименьшее общее кратное двух или более чисел — сначала умножить каждое из них на [латекс]1, 2, 3, 4[/латекс] и т. д. Например, найти наименьшее общее кратное [латекс] 2[/латекс] и [латекс]5[/латекс].
| Сначала перечислите все кратные [латекс]2[/латекс]: | Затем перечислите все числа, кратные 5: |
| [латекс]2\cdot 1 = 2[/латекс] | [латекс]5\cdot 1 = 5[/латекс] |
| [латекс]2\cdot 2 = 4[/латекс] | [латекс]5\cdot 2 = 10[/латекс] |
| [латекс]2\cdot 3 = 6[/латекс] | [латекс]5\cdot 3 = 15[/латекс] |
| [латекс]2\cdot 4 = 8[/латекс] | [латекс]5\cdot 4 = 20[/латекс] |
| [латекс]2\cdot 5 = 10[/латекс] | [латекс]5\cdot 5 = 25[/латекс] |
Наименьшее кратное, которое у них есть, будет общим знаменателем, используемым для преобразования каждой дроби в эквивалентные дроби.
См. пример ниже для демонстрации нашей задачи о пицце.
Пример
У одной пиццы, разрезанной на четыре ломтика, отсутствует один. Другая пицца того же размера была разрезана на восемь частей, три из которых были удалены. Опишите общее количество пиццы, оставшейся в двух пиццах, используя общие термины.
Показать решение
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями. Затем добавьте или вычтите числители над общим знаменателем.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Перепишите каждую дробь в виде эквивалентной дроби, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно сложить числители.
- Упростите, убрав все общие множители в числителе и знаменателе.
Упростить дробь
В математике принято представлять дроби в наименьшем выражении. Мы называем эту практику упрощением или сокращением дроби, и это может быть достигнуто путем сокращения (деления) общих множителей в числителе и знаменателе дроби.
Мы можем сделать это, потому что дробь представляет собой деление, и для любого числа [latex]a[/latex], [latex]\dfrac{a}{a}=1[/latex].
Например, чтобы упростить [латекс]\dfrac{6}{9}[/latex] вы можете переписать [latex]6[/latex] и [latex]9[/latex] , используя наименьшие возможные множители следующим образом:
[latex]\dfrac{6}{9}=\dfrac{ 2\cdot3}{3\cdot3}[/latex]
Поскольку [latex]3[/latex] есть и в числителе, и в знаменателе, а дроби можно считать делением, мы можем разделить [latex]3[ /latex] вверху и [latex]3[/latex] внизу, чтобы сократить до [latex]1[/latex].
[латекс]\dfrac{6}{9}=\dfrac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\dfrac{2\cdot1}{3}=\dfrac {2}{3}[/латекс]
В следующем примере показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Пример
Добавить [латекс]\Большой\фракция{2}{3}+\Большой\фракция{1}{5}[/латекс]. Упростите ответ.
Показать решение
Вы можете найти общий знаменатель, найдя общие кратные знаменателей.
Наименьшее общее кратное является самым простым в использовании.
Пример
Добавить [latex]\Large\frac{3}{7}+\Large\frac{2}{21}[/latex]. Упростите ответ.
Показать решение
В следующем видео вы увидите пример сложения двух дробей с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.
Подумай об этом
Добавить [латекс]\Большой\фрак{3}{4}+\Большой\фрак{1}{6}+\Большой\фрак{5}{8}[/латекс]. Упростите ответ и запишите в виде смешанного числа.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.
Показать решение
Вычитание дробей
Вычитание дробей выполняется так же, как и сложение. Сначала определите, одинаковы ли знаменатели. Если нет, перепишите каждую дробь как эквивалентную дробь с одинаковым знаменателем. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.
В приведенном ниже примере показано, как использовать кратные, чтобы найти наименьшее общее кратное, которое будет являться наименьшим общим знаменателем.
Пример
Вычесть [латекс]\Большой\фрак{5}{6}-\Большой\фрак{1}{4}[/латекс]. Упростите ответ.
Показать решение
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Умножение дробей
Точно так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями.
Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть [latex]\Large\frac{3}{4}[/latex] конфеты, и вы хотите найти [latex]\Large\frac{1}{2}[/latex] из [latex ]\Large\frac{3}{4}[/latex]:
Разделив каждую четверть пополам, вы можете разделить шоколадный батончик на восьмые части.
Затем выберите половину из них, чтобы получить [latex]\Large\frac{3}{8}[/latex].
В обоих вышеперечисленных случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
[латекс]\Large\frac{a}{b}\cdot\Large\frac{c}{d}=\Large\frac{a\cdot c}{b\cdot d}= \Large\frac{\text{произведение числителей}}{\text{произведение знаменателей}}[/latex]
Умножение более двух дробей
[латекс]\Large\frac{a}{b} \cdot\Large\frac{c}{d}\cdot\Large\frac{e}{f}=\Large\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex ]
Пример
Умножить [latex]\Large\frac{2}{3}\cdot\Large\frac{4}{5}[/latex]
Показать решение
Повторим: если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к ее упрощенной форме, удалив общие делители.
Например,
- Учитывая [латекс]\большой\фрак{8}{15}[/латекс], коэффициенты [латекс]8[/латекс] равны: [латекс]1, 2, 4, 8 [/latex] и факторы [latex]15[/latex]: [latex]1, 3, 5, 15[/latex]. [latex]\Large\frac{8}{15}[/latex] упрощен, потому что нет общих множителей для [latex]8[/latex] и [latex]15[/latex].
- Учитывая [латекс]\большой\фрак{10}{15}[/латекс], множители [латекс]10[/латекс] следующие: [латекс]1, 2, 5, 10[/латекс] и множители из [латекс]15[/латекс]: [латекс]1, 3, 5, 15[/латекс]. [latex]\Large\frac{10}{15}[/latex] не упрощается, поскольку [latex]5[/latex] является общим делителем [latex]10[/latex] и [latex]15[/latex]. ].
Прежде чем умножать две дроби, вы можете упростить, чтобы облегчить себе работу. Это позволяет вам работать с меньшими числами при умножении.
В следующем видео вы увидите пример того, как умножить две дроби, а затем упростить ответ.
Подумайте об этом
Умножить [латекс]\Большой\фракция{2}{3}\cdot\Большая\фракция{1}{4}\cdot\Большая\фракция{3}{5}[/латекс ].
Упростите ответ.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.
Показать решение
Разделение дробей
Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для покраски одного слоя краски на стенах комнаты требуется [латекс]3[/латекс] литра краски, и у вас есть ведро, содержащее [латекс]6[/латекс] кварт краски, сколько слоев краски краской можно красить стены? Вы делите [латекс]6[/латекс] на [латекс]3[/латекс] для ответа [латекс]2[/латекс] слоев. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс]\большой\фрак{1}{2}[/латекс] литр краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить [латекс]2[/латекс] на дробь [латекс]\большой\фракция{1}{2}[/латекс].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их произведение равно [латекс]1[/латекс] (не волнуйтесь, мы покажем вам примеры того, что это значит.)
- частное: результат деления
Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и получаете в результате [латекс]1[/латекс], тогда эти два числа являются обратными. Вот несколько примеров взаимного обмена:
| Оригинальный номер | Взаимный | Продукт |
|---|---|---|
| [латекс]\большой\фрак{3}{4}[/латекс] | [латекс]\большой\фрак{4}{3}[/латекс] | [латекс]\Large\frac{3}{4}\cdot\Large\frac{4}{3}=\Large\frac{3\cdot 4}{4\cdot 3}=\Large\frac{12 {12}=1[/латекс] |
| [латекс]\большой\фрак{1}{2}[/латекс] | [латекс]\большой\фрак{2}{1}[/латекс] | [латекс]\Large\frac{1}{2}\cdot\Large\frac{2}{1}=\Large\frac{1\cdot2}{2\cdot1}=\Large\frac{2}{ 2}=1[/латекс] |
| [латекс] 3=\Large\frac{3}{1}[/латекс] | [латекс]\большой\фрак{1}{3}[/латекс] | [латекс]\Large\frac{3}{1}\cdot\Large\frac{1}{3}=\Large\frac{3\cdot 1}{1\cdot 3}=\Large\frac{3 {3}=1[/латекс] |
| [латекс]2\Большой\фракция{1}{3}=\Большой\фракция{7}{3}[/латекс] | [латекс]\большой\фрак{3}{7}[/латекс] | [латекс]\Large\frac{7}{3}\cdot\Large\frac{3}{7}=\Large\frac{7\cdot3}{3\cdot7}=\Large\frac{21}{ 21}=\нормальный размер 1[/латекс] |
Иногда мы называем обратное «переворотом» другого числа: переверните [латекс]\большой\фрак{2}{5}[/латекс], чтобы получить обратное [латекс]\большой\фрак{5}{ 2}[/латекс].
Деление на ноль
Вы знаете, что значит делить на [латекс]2[/латекс] или делить на [латекс]10[/латекс], но что значит делить количество на [латекс]0[ /латекс]? Это вообще возможно? Можно ли разделить [латекс]0[/латекс] на число? Рассмотрим дробь
[латекс]\большой\фрак{0}{8}[/латекс]
Мы можем прочитать это как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.
[латекс]\текст{?}\cdot{8}=0[/латекс].
Мы можем сделать вывод, что неизвестное должно быть [латекс]0[/латекс], так как это единственное число, которое даст результат [латекс]0[/латекс] при умножении на [латекс]8[/латекс]. ].
Теперь рассмотрим обратную величину [латекс]\большой\фрак{0}{8}[/латекс], которая будет [латекс]\большой\фрак{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, у нас будет
[латекс]\текст{?}\cdot{0}=8[/латекс].
Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8.
Обратная величина [латекс]\большой\фрак{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено. .
Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа a [латекс]\большой\фрак{а}{0}[/латекс] не определен. Кроме того, обратная величина [latex]\Large\frac{0}{a}[/latex] всегда будет неопределенной.
Деление дроби на целое число
Когда вы делите целое число, вы умножаете его на обратное. В примере покраски, где вам нужно [латекс]3[/латекс] кварты краски для слоя и у вас есть [латекс]6[/латекс] кварты краски, вы можете найти общее количество слоев, которые можно покрасить, разделив [ латекс]6[/латекс] от [латекс]3[/латекс], [латекс]6\div3=2[/латекс]. Вы также можете умножить [латекс]6[/латекс] на обратную величину [латекс]3[/латекс], которая равна [латекс]\большой\фрак{1}{3}[/латекс], поэтому задача умножения становится
[latex]\Large\frac{6}{1}\cdot\Large\frac{1}{3}=\Large\frac{6}{3}=\normalsize2[/latex]
Деление равно умножению по обратному
Для всех делений вы можете превратить операцию в умножение с помощью обратного.
Деление равносильно умножению на обратное.
Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [latex]\Large\frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между [latex]5[/latex] людьми, каждый человек получает [latex]\Large\frac {1}{5}[/latex] доступных конфет:
[латекс]\Large\frac{1}{5}\normalsize\text{ of }\Large\frac{3}{4}=\Large\frac{1}{5}\cdot\Large\frac{ 3}{4}=\Large\frac{3}{20}[/latex]
Каждый человек получает [latex]\Large\frac{3}{20}[/latex] целого батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на [латекс]2[/латекс] или умножить каждый ингредиент на [латекс]\большой\фрак{1}{2} [/latex], чтобы найти новую сумму.
Например, деление на [латекс]6[/латекс] равносильно умножению на обратную величину [латекс]6[/латекс], которая равна [латекс]\большой\фрак{1}{6}[/ латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), среди [латекс]6[/латекс] людей?
Каждый человек получает один кусок, поэтому каждый человек получает [латекс]\большой\фрак{1}{4}[/латекс] пиццы.
Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.
Пример
Найти [latex]\Large\frac{2}{3}\div \normalsize 4[/latex]
Показать решение
Пример
Разделить. [latex] 9\div\Large\frac{1}{2}[/latex]
Показать решение
Разделить дробь на дробь
Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже нарезана на [латекс]4[/латекс] ломтика. Сколько существует фрагментов [latex]\Large\frac{1}{2}[/latex]?
Есть [латекс]8[/латекс] срезов. Вы можете видеть, что деление [латекс]4[/латекс] на [латекс]\большой\фрак{1}{2}[/латекс] дает тот же результат, что и умножение [латекс]4[/латекс] на [латекс]2. [/латекс].
Что произойдет, если вам нужно разделить каждый срез на три части?
У вас будет [латекс]12[/латекс] срезов, что равносильно умножению [латекс]4[/латекс] на [латекс]3[/латекс].
Деление дробями
- Найдите обратную величину числа, следующего за символом деления.
- Умножьте первое число (то, что перед знаком деления) на величину, обратную второму числу (после знака деления).
Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть». Это значит до СОХРАНИТЬ первое число, ЗАМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Пример
Разделить [latex]\Large\frac{2}{3}\div\Large\frac{1}{6}[/latex]
Показать решение
Пример
Разделить [latex]\Large\frac{3}{5}\div\Large\frac{2}{3}[/latex]
Показать решение
При решении задачи на деление путем умножения на обратное помните, что все целые числа и смешанные числа следует записывать в виде неправильных дробей. Окончательный ответ следует упростить и записать в виде смешанного числа.
В следующем видео вы увидите пример как разделить целое число на дробь, а так же пример как разделить дробь на другую дробь.
Операции с дробями
Мы открыты — звоните!
Позвоните сейчас, чтобы записаться на обучение
(888) 736-0920
HotmathMath Домашнее задание. Делай быстрее, учись лучше.
Сложение и вычитание дробей
Когда сложение и вычитание дробей , первое, что нужно проверить, — совпадают ли знаменатели.
Сложение и вычитание дробей с одинаковыми знаменателями
Если знаменатели совпадают, то это довольно просто: просто сложите или вычтите числители и запишите результат над тем же знаменателем.
Например,
Сложение и вычитание дробей с разными знаменателями
Если знаменатели не совпадают, то вы должны использовать равнозначные дроби, которые имеют общий знаменатель.
Для этого нужно найти наименьшее общее кратное (НОК) двух знаменателей.
Например,
Умножение и деление дробями
Умножение дроби на дробь
Чтобы умножить две дроби, просто умножьте числители, чтобы получить числитель произведения, и умножьте знаменатели, чтобы получить знаменатель произведения.
Например,
Умножение дроби на целое число
Чтобы умножить дробь на целое число, помните, что любое целое число можно записать в виде дроби .
Например,
Деление на дробь
Чтобы разделить на доля , умножить на взаимный фракции.
Например,
Разделять к .
Смотрите также: Умножение дроби на дробь , Умножение дроби на целое число и Деление на дробь
Объекты рядом со мной
- Серия 51 Курсы и занятия
- SAT Математические курсы и занятия
- SAT Предметный тест по химии Подготовка к экзаменам
- Серия 4 Курсы и занятия
- Награды Преподаватели французского языка Программа Курсы и классы
- Преподаватели межкультурных исследований
- Подготовка к экзамену на адвоката в Аризоне
- Преподаватели ISEE-Lower Level Quantitative Reasoning
- Курсы и классы для экзамена на адвоката в Пенсильвании
- QuickBooks Training
- Курсы по физике овсян.
